基于边坡滑坡工程地质的治理方法研究

李 金，王永胜，陈 勇

（1.中广核工程有限公司核电安全监控技术与装备国家重点实验室，广东 深圳 518172；2.长江三峡勘测研究院有限公司（武汉），湖北 武汉 430074）

1 研究意义

在自然历史发展下，随着地质构造的作用形成的具有临空面的地质体被称为斜坡（又称为边坡），这些边坡都有相应的高度与倾角。在漫长的地质历史时期中，即使是稳定的边坡也容易受到各种各样的内力或外力作用影响而导致边坡失去其本身的稳定性，其结果将导致边坡沿着某个滑动面发生位移变化，严重者甚至会对人类的生命财产安全构成威胁。我国是一个多山地的国家，有三分之二的土地是山地丘陵地貌，这也带来了大量的自然边坡与人工边坡，人们不可避免需要与这些边坡相接触，每年都有大量的滑坡灾害发生[3]。滑坡地质灾害问题已经成为了我国发生最频繁、分布最广泛、危害性和损失最大的地质灾害。

伴随着我国经济建设的高速发展，人类的活动范围不断扩大，在土地资源有限的影响下，人们不得不在一些地质条件不良的区域进行工程建设活动，加剧了因边坡失稳造成的破坏。滑坡灾害对我国国民经济、人民生命安全的威胁性极大，继续加大对其重视程度刻不容缓。由于影响滑坡稳定性的影响因素有很多，各个因素的影响程度往往又有很大的差异，因此对滑坡失稳破坏的变形演化过程进行量化十分困难，同时也增加了对滑坡灾害防治的难度。因此，研究滑坡的稳定性评价方法，给出滑坡稳定的评价准则对于后期边坡的预防治理，减少滑坡灾害的影响具有十分重要的意义[1]。

2 边坡稳定性研究国内外现状

滑坡灾害作为一种最为常见，并且分布范围最广的自然灾害，早已引起各国工程技术人员的极大关注。由于早期科学技术的缺乏，对边坡稳定性的研究多停留在以长期观测资料为基础的定性分析，这种方法误差较大，且没有统一的评判标准。20 世纪60 年代初，随着科学技术水平的发展，人们将力学机制更深入地应用到了对滑坡稳定性的计算之中，这期间刚体极限平衡法得到了普遍应用。进入80 年代以来，随着计算技术水平的快速发展，各种简便的分析算法应用到了滑坡的稳定性分析计算之中，使得越来越多的数值分析方法得到发展。随着新的理论与计算分析方式地提出，越来越多的工程师与学者将这些先进的方法采用到了对边坡稳定性分析的研究当中，他们努力尝试寻求更为贴切的方式对边坡进行最为精确的模拟分析，以期得到最为合理的结果。本文将采用极 限平衡法对滑坡的稳定性进行研究分析[2]。

3 工程实例分析

3.1 工程概况

金牛湖风景区项目位于金牛山北麓中段，该滑坡山体总体山势东高西低，坡度上陡下缓。经现场踏勘调查，滑坡后缘明显，滑坡后缘张拉开裂，下挫规模较大，总长约270m，平均高程70m，最大高程74.2m，下错高差1.5m。滑坡后缘上部山体覆盖层较薄，距上方后缘20m 左右即有基岩出露，下部滑坡土体堆积厚度较大。滑坡剪出口标高约22m。滑坡相对高差约35～52m，滑坡东西向宽290m，长200m，滑坡区投影面积约58000m2，根据地质灾害勘查，滑体平均厚度为5m，总滑坡方量约290000m3，属中型土质滑坡[3]。

3.2 滑坡区地质结构特征

根据地质剖面测绘及钻探等资料揭露，滑坡体组成物质主要为填土、耕植土、粉质粘土。填土主要为环山路路基，由水泥、黄沙、石子搅拌而成；耕植土结构较松散，厚度较薄，平均厚度1.5m，夹含植物根茎；粉质粘土粘粒含量高，呈硬塑状态。同时粉质粘土下部强风化安山岩，呈砂土状，透水性良好，遇水后强度急剧降低；由于下部强风化安山岩的透水性较好，且边坡上部基岩裸露，使得该层汇水能力强，这会使得上部粉质粘土层在水的作用下强度降低，因此可以判断滑面主要位于粉质粘土与强风化安山岩的土岩交界面。在该滑坡范围内设置几个测斜孔，通过其在不同时间内不同深度的位移情况可以大致判断边坡的滑动面位置基本位于粉质粘土与强风化安山岩的土岩交界面，符合边坡滑动的常见情况。

3.3 滑坡诱发机制、形成机制分析

该滑坡的形成受地形地貌、地质环境背景、气候降雨及人类工程活动等多种因素控制和影响。地形地貌、地质环境背景是其形成的基础条件，气候降雨等外在因素往往是促进其发展的诱导因素。根据现场踏勘调查结合相关勘查资料，该滑坡山体地形呈现上陡下缓的形态。滑坡体主要由粉质粘土组成，下伏基岩为强～中风化安山岩，基岩面近似同山体地形呈上陡下缓状态。岸坡长期受湖水的冲刷；同时滑坡中部进行过道路建设，人为改变坡体原有地形改造，使局部坡体处于临空状态。随着降雨长期的冲刷，山体上部土体受雨水裹挟向下部汇集，最终沉积于滑坡体中上部，使得滑坡体中上部土层覆盖层较厚；同时，由于滑坡区上部基岩面裸露，区域内汇水面积、汇水量较大，降水极易沿渗透性良好的强风化岩层入渗并汇集，强风化安山岩风化强烈呈砂土状，遇水后结构易破坏，抗剪强度急剧降低，此外还使得上覆粉质粘土层在水的影响下抗剪强度降低，最终上覆土层在饱和自重及地下水渗流等作用影响下发生下滑。滑动土体变形挤压下部土体，使得下部土体下滑力增大，当下部土体抗滑力难以维持坡体稳定时便随上部滑体一并下滑，最终促使该处发生滑坡。

由以上分析，该滑坡的形成主要是由于长期的降雨条件下，使得边坡上部土体堆积在中上部，滑坡上部基岩裸露使得雨水更易聚集在强风化层，降低了上部粉质粘土的抗剪强度。如果滑坡发生整体失 稳产生滑动，将直接威胁区内居民的生产和生活、影响灾后重建工作，给当地经济建设造成不必要的损失。由此可见，滑坡是岩土工程领域极富挑战性的问题，加强对滑坡稳定性分析方法的研究具有重要意义。

4 边坡稳定性分析方法

4.1 安全系数定义

利用极限平衡法对边坡进行稳定性分析计算是目前最成熟简便的一种方法，其结果较为可靠。虽然极限平衡法的计算方法种类有很多，但无论采用哪一种方法，其根本目的在于求解边坡的稳定性安全系数，这样才能给边坡是否稳定确认一个标准，以此来对边坡的后续治理防护提供一个可应用的数据。基于强度储备的安全系数、超载储备安全系数以及下滑力超载储备安全系数是当前对边坡稳定性评价采用最为普遍的三种稳定性安全系数，其表达式分别为：

基于强度储备的安全系数Fs1：

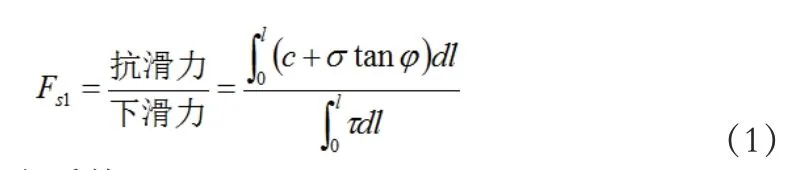
超载储备安全系数Fs2：

下滑力超载储备安全系数Fs3：

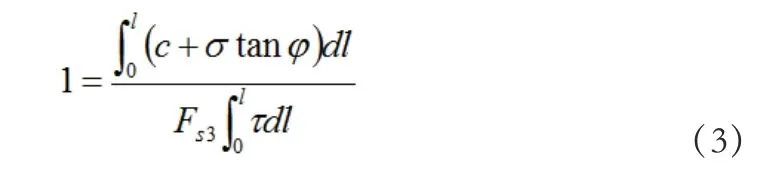
式1～3 中，c 是滑坡体的粘聚力、σ 是滑坡沿滑动面的法向应力、ϕ 是内摩擦角、l 是滑线长度、τ 是下滑力。

其中基于强度储备的安全系数，是采用降低边坡岩土体强度直到边坡处于失稳边缘，来确定安全系数的；超载储备安全系数是利用荷载的逐级增大，直到边坡失稳，增大比例即为所欲求得的安全系数；下滑力超载储备安全系数即是通过增大下滑力但不增大抗滑力，使得边坡失稳来计算安全系数。边坡稳定性分析计算的方法有许多，不同的方法其采用的安全系数计算方式也有所区别，在本文中所利用的传统的极限平衡法常采用的安全系数是下滑力超载储备安全系数，而采用的FLAC-3D 法其内嵌的强度折减系数法则采用的是另一种安全系数即强度储备安全系数。

FLAC-3D 软件采用的是强度储备安全系数，也被称为强度折减安全系数。是将边坡视为一个整体，对边坡的强度指标进行一定比例的缩减，通过得到边坡土体沿某一滑动面滑移破坏时的折减比例来确定其稳定性安全系数的方法。但是，在实际工程中，滑动面不同部位的强度折减安全系数并不相同，该方法并不能完全反映滑坡体的稳定性系数真实值，其获得的结果只能视作整个滑动面上各点安全系数的平均值。

4.2 常见的极限平衡法分析

目前极限平衡法在均匀土质边坡和岩质边坡中的应用较为广泛。对于土质边坡而言，圆弧法是最为常见的一种分析方法，通过简单的力学方法并结合一些对边坡稳定性影响较小的力学假设来计算出安全系数。对于极限平衡法来说，滑动面的确定十分重要。早期对极限平衡法滑面的假定为一个圆弧面，但实际上它的形状可是圆弧面、平面、折线或者其他不规则曲面。由于滑动面的不确定性，为了得到边坡的实际稳定性状况，往往需要对多个滑面进行计算以便获得最危险的滑面位置。目前常见的极限平衡法有瑞典条分法、毕肖普法、Janbu 法、Morgenstern-Price 法。

4.2.1 数值分析方法

第一类是有限单元法，这是是一种基于连续介质力学的分析方式。它通过把研究区域划分为有限个小区域，并将其称为单元，单元间的连接点称为节点。通过把边坡模型进行单元离散化来对各个单元进行分析求解，结合边界条件以此来获得边坡单元的应力应变关系和整体边坡的屈服区域。有限元分析方法考虑到了边坡的应力和应变间的本构关系，相比于极限平衡法更为精确，并不受边坡形状和材料的干扰限制。有限元的求解结果能够简便直观地得到边坡的应力、位移和应变增量等信息，这是极限平衡理论难以获得的，可见有限元分析方法是一种较为理想的分析边坡稳定性的分析方式。但其在对边坡模型的构造、边界条件的选择、初始应力状态和弹塑性本构关系的确定方面有着一定的难度，该方法的缺陷是不能很好地去求解非连续介质问题，对于大变形问题的解答误差往往很大。随着研究的不断深入，有限元在边坡稳定性分析中得到了迅速的发展，目前基于该方法的应用有圆弧搜索法和强度折减法等。有限元圆弧搜索法利用有限元这一计算方法较为准确地得到了边坡的下滑力和抗滑力。强度折减法是在利用该方法对边坡进行分析时，不断缩减岩土体的强度参数来得到边坡的稳定性系数。这一方法的优势是不需要去提前确定一个虚拟的滑动面，应用性很强。通过对目前主流的几种边坡稳定性计算方法进行分析对比，在对滑坡的稳定性计算结果分析中得出有限元法是一种计算精度高，并能模拟出状态变化的实用性强的边坡稳定性分析方法[4]。

有限元法的研究对象往往是连续介质，但实际的岩土体却是一种非连续，各项异性的材料，为了能更真实地模拟计算边坡的稳定性，处理非连续介质的数值分析方法得到了十足的发展。这其中有Cundall（1979）提出的分析非连续性颗粒状材料性质的新型方法DEM 方法（离散单元法）和以此为基础发展出来的FLAC 法(快速拉格朗日法），这一方法能够有效地去处理那些非连续性材料，适用于土质边坡的实际情况。石根华（1988）在离散元的基础上提出了一种适合处理非连续节理化岩土的方法DDA 方法（非连续变形分析方法）。石根华结合流形中的有限覆盖技术建立了流形方法，使得连续变形与非连续变形问题的统一分析成为可能。在边坡稳定性分析中，非确定性分析方法的应用也较为普遍，如可靠性分析、灰色系统理论、系统分析方法等。随着计算机技术的快速发展，基于GIS 与GPS 的计算机仿真技术也逐渐在边坡稳定分析中得到了大量的应用发展。

4.2.2 Ordinary 法

Ordinary 法是边坡稳定性分析计算中最早的极限平衡法，又叫Fellenius 法即瑞典条分法。这种方法将条块重量在滑面法向的分解量作为滑面的法向力。该方法假设滑动面为圆弧面，且对土条侧向的力合力方向与土条的底面平行。该方法通过建立土条底面法线方向静力平衡方程和力矩平衡方程，确定安全系数Fs：

在均质土中取宽度相同的土条，则可将上述公式简化为：

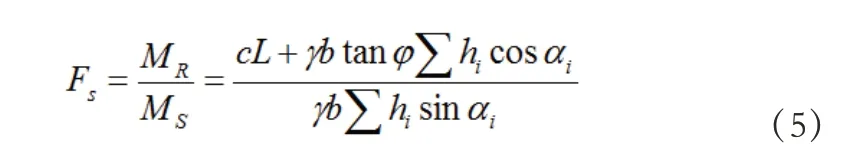
式4～5 中，MR为抗滑力、MS为下滑力、c 为粘聚力、ϕ 为内摩擦角、li为第i 条块底面长度，L 为圆弧滑面的弧长、iW 为第i 条块重量、γ 为土条重度、b 为土条底面宽度、ih 为第i 条块侧向高度、αi为第i 条块土条重力方向与滑动面法向方向的夹角。

通过假定不同的滑动面位置，找到的最小Fs 极为该滑坡的稳定性系数。但由于该法忽略了条块体之间的作用力，不能满足所有的平衡条件，由此算出的稳定性安全系数偏低。Ordinary 法只是考虑了下滑力矩与抗滑力矩的平衡，没有对临界滑动面及最小安全系数进行深入的研究，而Slope/W 软件基于有限元方法可以得到一系列单元体的安全系数，以此作出等值线来确认边坡的临界滑动面，提高了该方法的精度[5，6]。

4.2.3 毕肖普法

毕肖普法是1955 年毕肖普基于瑞典条分法进行优化而得出的一种计算方式，这种方法保留了瑞典条分法对滑面现状的假设和求解安全系数的平衡条件。相比于瑞典条分法，该方法考虑了土条两侧的作用力和土条底部法向力，主要是对条间作用力在法线方向的作用。对于多余的未知力进行假定，假定土体切向力为0 且在土条两侧所受到的作用力方向是水平方向。

通过对圆心的力矩平衡解得的安全系数Fs 为：

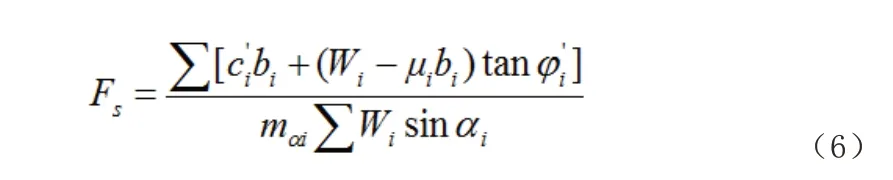
式6～7 中，mαi为第i 个条块计算系数、αi为第i 个条块底部倾角、Wi第i 个条块重量、为第i个条块粘聚力、为第i个条块有效内摩擦角、ib 为第i个条块长度、μi为第i个条块孔隙水压力。

Bishop 法考虑了条块两侧的反力，但均假定反力为水平方向，该方法也只是满足了力矩平衡和沿条块垂直方向力的平衡，没有对临界滑动面及最小安全系数进行深入的研究，而Slope/W软件基于有限元方法可以得到一系列单元体的安全系数，并以此作出等值线来确认边坡的临界滑动面，提高了该方法的精度。

4.2.4 Janbu 法

瑞典条分法和毕肖普法都是假定滑动面为圆弧状或近似圆弧状，这两种方法主要的研究对象为土质边坡，但在实际工程中滑坡并不一定都是圆弧状的滑动面。Janbu 法可以满足所有的静力平衡条件，是严格的方法之一，这种方法解决了滑动面不是圆弧状的问题。在该方法采用的假定条件是假定了条间作用力的位置在土条底面以上1/3 高度，对每个土条进行水平和垂直方向上力的平衡计算，结合摩尔库伦破坏准则解得该方法的稳定性系数为：

式中mi为：

式8～9 中，im 为第i 个条块计算系数、αi为第i 个条块底部倾角、iW 第i 个条块重量、ci为第i 个条块粘聚力、ϕi为第i 个条块内摩擦角、ib 为第i 个条块长度、∆Xi为第i 个条块条间切向力。

该方法需要采用迭代的计算方式逐步逼近真实的稳定性安全系数Fs。Janbu 法同时考虑了力和力矩平衡条件，且计算过程可以通过手算或编写相应的程序来得到结果，精确度较高。但是在实际应用过程中有可能遇到不收敛情况，需要注意。Janbu 法适用于非圆弧型滑动情况，公该方法满足了力和力矩的平衡条件，较为精确。但是如果土条内摩擦角较小或者是条块的宽度太小都将可能使得计算结果出现不收敛现象。

4.2.5 Morgenstern-Price 法

Morgenstern-Price 法也是一种同时满足力与力矩平衡条件的分析方法，它将滑动面，条块重力以函数关系式表现出来，例如它用函数y=z（x）表示边坡滑移体的坡面线：（x）表示边坡滑动体推力作用线。Morgenstern-Price 法是当前用来对具有圆弧状滑动面边坡计算方法中最为严格的一种算法。陈祖煌扩展了这一方法的算法，通过最优化的方法获得临界滑动面，并通过编制了有关的程序来进行求解计算。Spencer 法是Morgenstern-Price 法的一个特例。

4.2.6 剩余推力法

剩余推力法是我国工程技术人员自主创立的一种稳定性分析方法，该方法又被称为传递系数法或不平衡推力法。这种稳定性计算方法简单方便而且能够为边坡的治理设计提供所需要的下滑推力，被广泛应用到了我国水利工程、交通工程中的滑坡治理分析。这种方法常用来进行滑动面为折线型的边坡稳定性计算。该方法假设滑动体单元内部不会有相互挤压力，即各单元属于刚性体，来自上一个单元的剩余下滑力方向与上一单元的底面平行且单元间只传递压力，没有拉力，即当任意单元的推力为负值时，它对下一单元的传递推力为0。最终得到的滑坡稳定性安全系数表达式为：

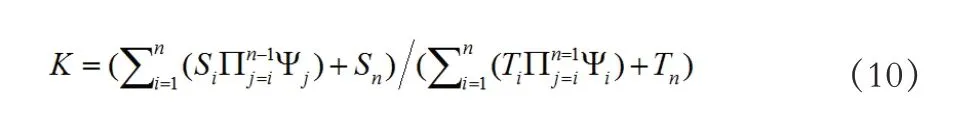
式10～11 中，K 为安全系数、Si为第i 个条块抗滑力、Ψj为第i 个条块传递系数、iT 为第i 个条块下滑力、αi第i 个条块底部倾角。

5 研究结论

滑坡地质灾害在天然状态下稳定，在强降雨状态下容易发生滑动，体现了降雨对滑坡地质灾害的影响很大。降雨入渗后，一方面增加了岩土的重度，加大了坡体重量，另一方面使岩土体的抗剪强度降低，加速了滑坡的产生。鉴于此，本文通过极限平衡法对地质滑坡进行了稳定性分析，利用极限平衡法来求得边坡的稳定性系数，以此判断滑坡的稳定性。