拉萨河城区段治理工程开挖深基坑稳定性分析

牛平平，李栋梁，王 蒙，贺 苗，黄 伟，李乃回，祁国军

(徐州市水利建筑设计研究院，江苏 徐州 221000)

河道整治工程中，常见的地层为杂填土、素填土、粉质黏土、淤泥、砂卵石层等结构较为松散、强度较为低下的岩土体。在临近河水区域修建水利建筑物时，往往需要对河道进行开挖形成深基坑，因此准确分析基坑的稳定性尤为重要。袁宗浩等对偏压作用下基坑底部隆起进行分析，获取了抗隆起上限值；黄伟笑研究了多级开挖对边坡稳定性的影响；刘汉露等使用未确知测度方法对基坑开挖后的边坡稳定性进行预测评价；王潇宇、王中达等使用强度折减法对基坑开挖后的稳定性进行数值模拟分析，数值模拟结果可为工程设计提供参考。目前，有较多的专家学者针对数值模拟方法和卵石层深基坑稳定性问题进行了专项研究，并取得了较为丰硕的成果。本文在前人研究基础上，结合拉萨河城区段治理工程，对河流区域深基坑开挖稳定性进行研究，以期为工程支护提供参考。

1 工程概况

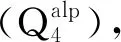
2 深基坑稳定性分析

影响深基坑开挖稳定性的因素较多，主要有地层结构、支护方案、施工工艺、地下水类型等。结合拉萨河城区段该拦河闸工程，建立离散元(PFC)数值模拟模型如图1所示，对临河富水厚层砂卵石地区深基坑开挖的稳定性问题进行研究。

一般情况下，在深基坑开挖施工过程中需要设置多个降水井，将地下水水位降至基坑底部以下，因此，本次数值模拟分析不考虑地下水对基坑稳定性的影响。采用PFC进行数值模拟分析时，将所研究的岩土体划分为多个离散单元，力学模型较为简单。

2.1 数值模拟模型建立

在卵石地区，常用的支护方法有支护桩和内支撑。此次水闸开挖基坑为长方形，典型地质断面为：杂填土(0～2.0m)、粉质黏土(4～6m)、细砂(6～7m)、卵石层(7～21m)、泥岩(21～30m)，此次泥岩未揭穿，深基坑采用支护桩和钢支撑方法。设计支护桩桩长为24.0m，共架设4道钢管横撑。由于基坑地层分布较为均匀，因此仅选择一个断面进行数值模拟分析。

2.2 计算参数选取

数值模拟计算参数的选取主要是根据现场原位试验、周边工程经验以及室内力学试验，各地层数值模拟参数见表1。

表1 各地层数值模拟参数

图1 PFC数值模拟图

2.3 钢支撑施工时间确定

数值模拟计算步骤主要是依据深基坑开挖施工工艺确定。本工程采用明挖法，进行分层开挖，并依次架设钢支撑，在施工过程中，优化钢支撑的施工时机，以保证深基坑的稳定性和施工进度需求。为了确定首道支撑的最优时间，使用数值模拟方法确定深基坑直接开挖的极限深度，计算结果见表2。

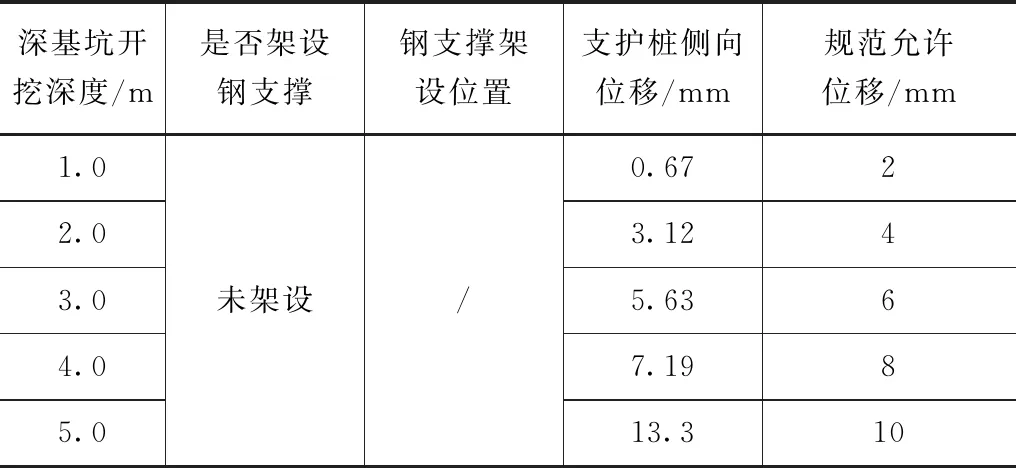
表2 第一道钢支撑施工时间

由表2计算结果可知，在不采取钢支撑的情况下，当开挖深度达到5.0m时，支护桩侧向位移大于规范允许值，因此，第一道支撑位于表面以下0.5m处。为了确定第二道支撑的施工时间，数值模拟计算结果见表3。

根据表3计算结果可知，在-0.5m处设置第一道钢支撑情况下，当开挖深度达到7.0m时，支护桩侧向位移大于规范允许值，因此，第二道支

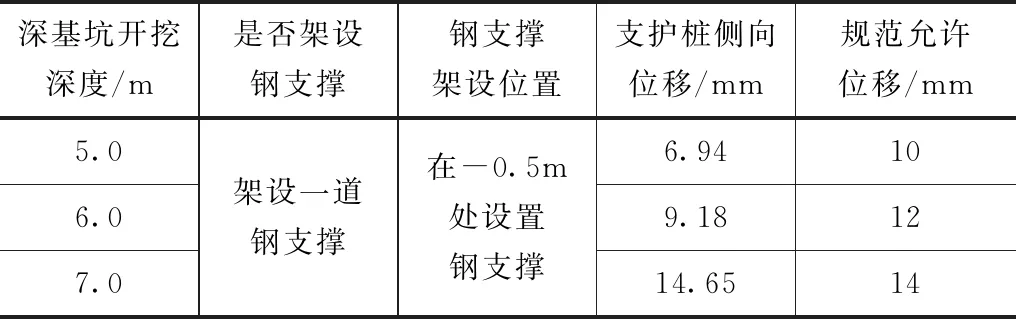
表3 第二道支撑施工时间

撑位于表面以下5.0m处。为了确定第三道支撑的施工时间，数值模拟计算结果见表4。

表4 第三道支撑施工时间

根据表4计算结果可知，在-0.5m、-5.0m处设置第一道、第二道钢支撑情况下，当开挖深度达到12.0m时，支护桩侧向位移大于规范允许值，因此，第三道支撑位于表面以下10.0m处。为了确定第四道支撑的施工时间，数值模拟计算结果见表5。

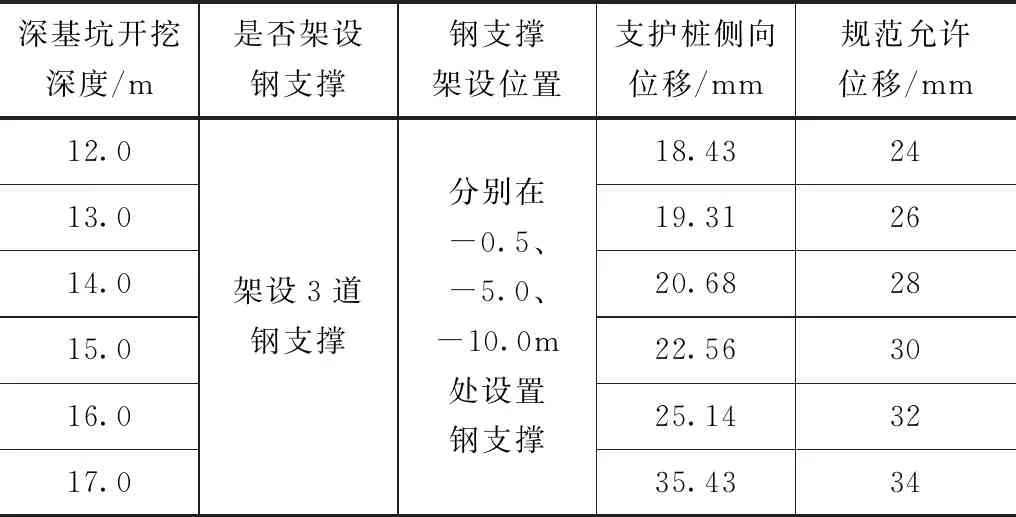
表5 第四道支撑施工时间

根据表5计算结果可知，在-0.5、-5.0、-10.0m处设置第一道、第二道、第三道钢支撑情况下，当开挖深度达到17.0m时，支护桩侧向位移大于规范允许值，因此，第四道支撑位于表面以下15.0m处。四道钢支撑施工后，基坑变形结果见表6。

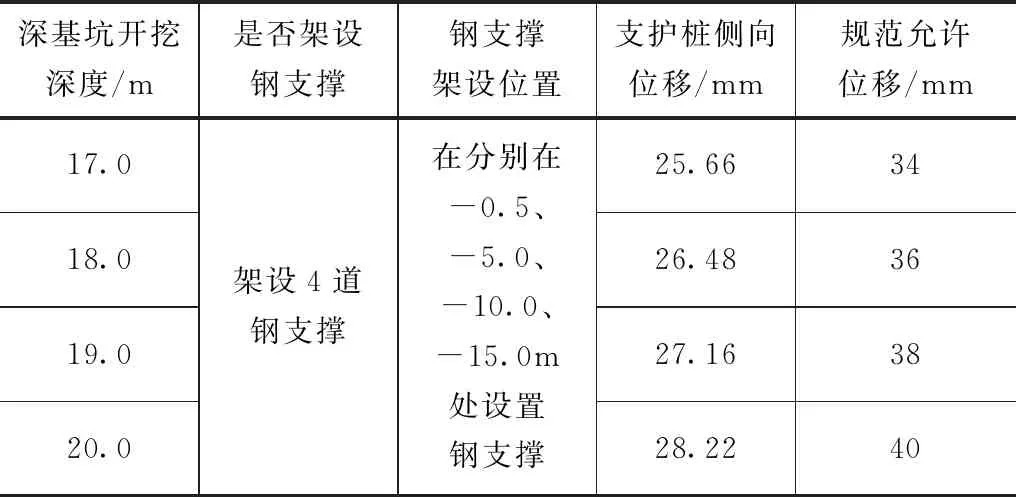
表6 四道钢支撑完成后变形结果

根据表6计算结果可知，设置四道钢支撑后，基坑变形结果满足规范要求，因此，不必加设第五道钢支撑。

2.4 支护桩水平方向位移分析

根据上述研究结果，确定数值模拟开挖步骤，见表7。

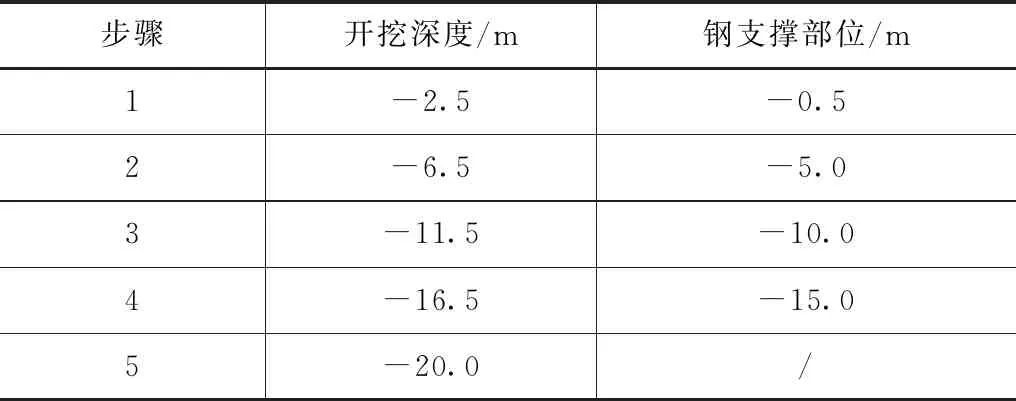
表7 基坑模拟步骤

各步骤的支护桩水平方向变形结果如图2所示。从图2中可知，开挖后，变形曲线呈现出典型的中间大、两头小的特点。随着开挖深度的不断增加，支护桩相同部位水平方向位移不断增大，桩体最大位移部位也逐渐下移，在基坑开挖深度范围内，支护桩各处水平位移均小于30.0mm，满足设计规范要求。

图2 变形结果

3 结论

拉萨河深基坑开挖工程较为复杂，砂卵石层分布厚，采用PFC数值模拟方法确定钢支撑的施工时间。根据数值模拟结果，采用4道钢支撑可以满足基坑稳定性要求，各处钢支撑分别位于-0.5、-5.0、-10.0、-15.0m处，根据绘制支护桩的水平方向位移，支护桩在第五次开挖后，变形仍然小于30.0mm，满足规范要求。