基于MIDAS某大型初雨调蓄池边墙结构分析
龚存燕
(深圳市水务规划设计院股份有限公司,广东 深圳 518008)
1 研究背景
随着城市发展,城市对环境的要求不断提高,越来越多的初雨调蓄池应运而生。初雨调蓄池作为一种地下水池结构,有着传统地下水池和地下室的功能,但同时结构形式又有别于传统地下水池和地下室,调蓄池深度从以前几米至现在十几米,面积由原来几千平方米发展到现在几万平方米,另外功能方面也逐渐由原来单一功能调整为综合雨水花园或市政公园等,随着调蓄池功能方面的转变,对调蓄池结构安全也提出更高的要求,调蓄池造价相应增加。如何才能保证调蓄池结构安全又经济合理,特别是对于调蓄池高度高而边墙支撑结构方面又仅能设置顶部一层楼板情况。本文基于MIDAS三维有限元软件,分析某大型调蓄池顶板、顶部主次梁、中间连梁以及底板对边墙结构位移和受力的影响,同时将有限元计算结果与简化计算进行对比,为类似地下工程设计提供参考。
2 计算模型及参数
2.1 调蓄池基本参数
某大型初雨调蓄池工程等级为Ⅱ等,主要建筑物级别为2级,调蓄池采用地下式,规模为1.5万m3,调蓄池长87.2m,宽33.0m,池顶覆土厚度为2.0m,顶部为市政公园,调蓄池高10.85m,单元尺寸为6.0m×6.0m,顶板厚0.3m,顶部主梁截面尺寸为0.5m×1.0m(宽×高),次梁0.4m×0.8m,立柱0.8m×0.8m,边墙和底板厚度均为1.0m(边墙下端和底板端部厚1.5m),在距底板顶6.3m处布置一道连梁,连梁截面尺寸为0.5m×1.0m,调蓄池典型断面如图1所示。

图1 调蓄池典型断面图
2.2 计算软件选择
为便于模拟顶板、底板、顶部主次梁和连梁对边墙受力的影响,本次采用MIDAS三维有限元软件中GTS子块进行建模计算。MIDAS/GTS(Geotechnical and Tunnel analysis System)目前广泛用于地下工程项目与结构分析计算中,基本上涵盖了岩土方面所有的分析计算功能,可用于求解关于岩土工程施工阶段模拟,渗流分析,固结分析,边坡稳定分析,动力分析,衬砌、锚杆的结构分析等领域;其功能多样,如前处理能力高效:中文界面、CAD风格几何建模、丰富多样网格划分、内置各种建模助手,专业的单元库和本构模型,以及完美的后处理:组合包络结果,等值线、矢量、剖断面输出云图,动画、表格、计算书等。
2.3 计算模型
为便于分析顶板和梁系结构等对边墙受力影响及有限元建模,本次模型进行如下简化:①不考虑边墙下端和底板端部加厚的影响,边墙和底板厚度均为1.0m考虑;②不考虑顶板顶部开孔的影响,不考虑存水室中、边隔墙的影响,以及不考虑出水泵井高程的影响,与调蓄池底板高程同高考虑,不考虑设备廊道室上部结构以及调蓄池下池楼梯间等的影响;③不考虑下部抗浮桩的影响。
本次对于边墙、底板和顶板采用面单元,立柱、连梁及顶板主次梁采用梁单元,根据上述简化等进行建模,本次共建立节点32610个,单元35808个,其中面单元30336个,梁单元5472个。如图2所示。
本工程约束对于边墙外端按自由边界考虑,对底板和边墙底部考虑固定约束。
图2 调蓄池三维有限元网格图
2.4 计算参数
本工程调蓄池各部分结构均采用C35钢筋混凝土结构,弹性模量为3.15×107kN/m2,泊松比为0.167,容重为25kN/m3。
为便于比较调蓄池顶板和梁系结构等对边墙的影响,本次计算仅考虑侧土压力对边墙的影响,本次地下水按位于设计地面0.5m以下考虑,基坑回填采用中粗砂,根据《工程地质手册(第五版)》第1039页的表8- 3- 15中产生主动土压力所需的最小位移对于砂土平移为0.001H、转动为0.001H(H为墙高),采用《建筑结构静力计算手册(第二版)》第103页一端剪支一端固定模型计算,边墙采用主动土压力公式计算墙体的最大挠度为2.2mm,本工程边墙产生主动土压力所需最小平移(或转动)为10.5mm,因此本次边墙内力计算采用静止土压力水土分算公式成果,侧土压力系数取为0.4,经计算,边墙上部土压力设计值为38.72kN/m,底部为206.72kN/m。
3 计算结果分析
3.1 调蓄池边墙简化计算模型
常规设计时,将调蓄池各层楼板、基础底板等作为调蓄池挡土墙的支撑,计算模型通常按下列方式处理:顶板处简化为铰接,基础底板处简化为固端,其他楼层作为连续支座,将调蓄池边墙按1m宽板带简化为多跨连续梁进行内力计算和配筋,不考虑梁系结构的影响。
本次调蓄池边墙简化计算模型为顶板铰接、底板固端的单跨梁,不考虑顶部主次梁和中间连梁对边墙受力的影响。
3.2 顶板厚度对边墙受力影响分析
不考虑调蓄池底板和梁系结构情况下,分别计算顶板厚度为0、0.05、0.12、0.3m情况,有限元计算及简化计算沿高度边墙位移、弯矩值及分布情况,如图3所示,结果见表1。
由表1和图3可知:
(1)有无顶板对边墙位移和弯矩影响很大,顶板能大幅减小边墙上端位移值和下端弯矩值。
(2)有顶板时边墙位移和弯矩值沿高度分布规律与简化计算相近,相应位置的对应值也接近,但简化计算会导致边墙位移值偏小,特别是顶板厚度越薄,偏小幅度越明显,同时简化计算会导致边墙下端弯矩值偏大中间偏小,顶板厚度越厚,下端偏大中间偏小幅度越明显。
(3)根据顶板厚度不同边墙下端弯矩变化规律,顶板厚度过薄会导致有限元计算边墙端部弯矩值大于简化计算值,因此当顶板厚度过薄时,顶板仍简化为铰接进行设计会对边墙下端受力不利,但因水工结构中顶板厚度一般不会小于0.12m,因此楼板简化为铰接进行设计不会导致边墙下端受力不利。
3.3 中部连梁及顶板主次梁对边墙受力影响分析
不考虑调蓄池底板和顶板结构情况下,分别计算顶板主次梁、中间连梁对边墙位移及弯矩的影响,具体结果见表2、如图4和图5所示。
由表2和图4可知:
(1)有无中间连梁对边墙位移和弯矩影响均较大,连梁的存在能较大幅度减小边墙上端位移值和下端弯矩值。
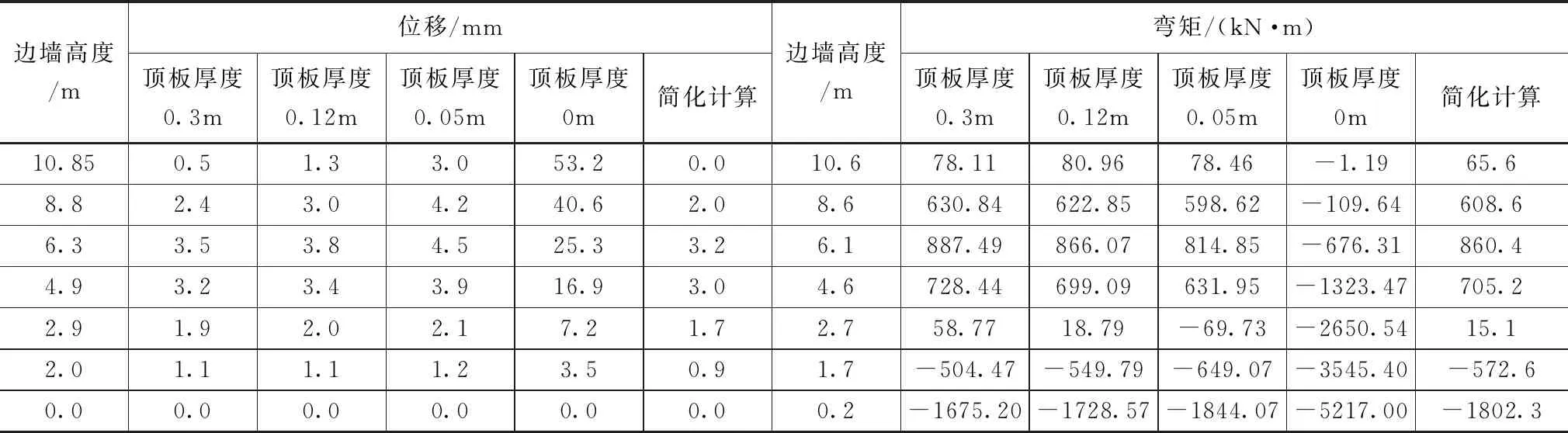
表1 不同顶板厚度情况下边墙关键点位移及弯矩值表
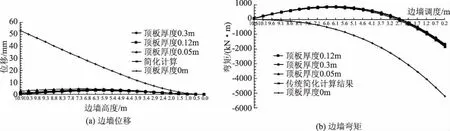
图3 不同顶板厚度情况下边墙位移及弯矩沿墙高分布图
(2)在调蓄池中间设置连梁时,边墙位移沿高度分布规律与边墙顶端自由接近,但位移值减小较多,特别是中上部边墙位移值,但减小幅度受连梁截面尺寸影响,随着截面尺寸增大位移值减小;连梁下部边墙位移值与简化计算结果接近。
(3)在调蓄池中间设置连梁时,边墙弯矩沿高度分布规律与边墙顶端自由类似,但端部弯矩值较边墙顶端自由情况的弯矩值减小较多,减小幅度也受连梁截面尺寸影响,随着截面尺寸增大弯矩值减小,连梁截面尺寸增大到一定程度时,边墙下端弯矩较简化计算结果小。
由表2和图5可知:
(1)有无顶部主次梁对边墙位移和弯矩影响均较大,顶部主次梁能较大幅度减小边墙上端位移值和下端弯矩值。
(2)在调蓄池顶部设置主次梁时,边墙位移沿高度分布规律与简化计算接近,但相应高度位移值大于顶部设置楼板情况的位移值;但当考虑顶部主次梁与中间连梁共同作用时,其对边墙位移的减小作用大于仅顶部设置楼板情况,特别是对中部最大位移减小相对明显,可使边墙最大位移小于简化计算情况。
(3)在调蓄池顶部设置主次梁时,边墙弯矩沿高度分布规律与简化计算类似,特别是在中间连梁共同作用下可以较大幅度减小边墙中部和下端弯矩值,对改善边墙弯矩有利。

表2 考虑调蓄池梁系结构时边墙关键点位移及弯矩值表

图4 考虑调蓄池连梁结构时边墙位移及弯矩沿墙高分布图

图5 考虑调蓄池顶部主次梁时边墙位移及弯矩沿墙高分布图
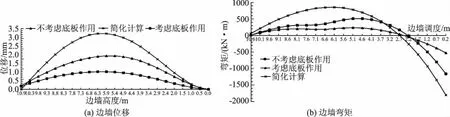
图6 考虑底板时边墙位移及弯矩沿墙高分布图
3.4 底板对边墙受力影响分析
在考虑顶部楼板和梁系结构基础上,分析有无底板边墙位移和弯矩沿高度分布情况,具体如图6所示。
根据图6可以看出,考虑底板情况下边墙位移和弯矩沿高度分布规律与简化计算和顶部有楼板情况相近,但底板的存在能较大幅度地减小边墙中部位移值和边墙下端弯矩值。
4 结论
(1)根据本次有限元计算结果,按静止土压力公式计算边墙土压力更合理。
(2)对顶部楼板厚度超过0.12m的调蓄池边墙按上端铰接和下段固定进行设计时,其下端弯矩是偏安全的。
(3)在调蓄池高度较高时,为节约投资和避免设计过于保守,除考虑顶部楼板对边墙弯矩的作用外,还应考虑调蓄池梁系结构和底板对其受力有利的影响。
本工程楼板、边墙采用的是二维单元,梁系结构采用的是一维单元,若采用三维实体单元进行模拟,结果会更接近实际,另外本次计算也未考虑土体以及基础对边墙受力的影响。

