基于加权t-SNE和偏离度的捷联惯组稳定状态评估方法

李 亚，徐军辉，单 斌，甄占昌

基于加权-SNE和偏离度的捷联惯组稳定状态评估方法

李 亚，徐军辉，单 斌，甄占昌

（火箭军工程大学导弹工程学院，西安，710025）

针对传统的捷联式惯性测量组合（Strapdown Inertial Navigation System，SIMU）稳定性分析方法存在的仅能定性评价、不能量化比较的缺点，基于数据驱动的方法，提出一种利用改进的加权-分布领域嵌入（-Distributed to Chastic Neighbor Embedding，-SNE）的流形学习方法提取数据中的低维流形特征，然后计算各样本与参考样本偏离度的方法对捷联惯组的稳定状态进行评估。在实例验证中，对比了使用普通-SNE和加权-SNE的降维效果，并使用-最近邻分类算法分析了欧氏距离、标准化欧氏距离、马氏距离、熵值法和熵权-灰色关联分析法这5种常用的偏离度计算方法的评估效果，证明了所提出方法的有效性。

捷联惯组；状态评估；流形学习；-SNE；加权；偏离度

0 引 言

长期以来，使用单位仅能通过传统的稳定性分析来定性地判断捷联惯组是否处于稳定状态，对于不稳定的捷联惯组需重新标定甚至返厂维修，造成了巨大的人力、经济负担。因此，对捷联惯组的稳定状态进行定量评估，有助于使用单位更清楚地了解捷联惯组的稳定状况，为捷联惯组的选用、定期测试提供指导；同时，对于使用了高精度捷联惯组的重要装备，在构建其故障预测与健康管理[2]（Prognostic and Health Management，PHM）系统时，捷联惯组的稳定状态评估也能作为其中的一个重要组成部分。

目前，针对复杂设备的状态评估主要有3种，基于模型驱动的方法、基于数据驱动的方法和基于知识的方法。其中基于数据驱动的方法由于对系统模型的解析表达式和先验知识没有严格的要求，已经在旋转机械、车辆、化工等领域得到了广泛的应用[3~6]。谷梦瑶等[4]提出一种多退化变量下基于实时健康度的相似性寿命预测方法，该方法将样本与正常样本的差异量化为健康度，然后基于相似性进行寿命预测，并在陀螺仪寿命预测的实例验证了该方法的优越性；谷广宇等[5]提出了一种基于改进K-means聚类算法的发动机状态评估方法，通过合理赋权、最小方差启发式初始聚类中心优选和Bootstrap小子样统计方法较好地在缺少先验知识和小样本条件下，进行发动机状态评估难度大的问题；赵帅等[6]通过拉普拉斯特征降维与马氏距离分析模型对滚珠丝杠性能衰退程度进行量化评估，并对比常见方法验证了其有效性。

本文基于数据驱动的方法，提出了一种基于加权的-分布随机领域嵌入算法（-Distributed to Chastic Neighbor Embedding，-SNE）和偏离度的捷联惯组的稳定状态评估方法。首先确定了捷联惯组的稳定状态指标，并使用Pearson相关系数和最大信息系数分析了某型捷联惯组稳定状态指标的相关关系，证明了使用非线性特征提取方法的必要性；然后改进了-SNE方法，使用提出的加权-SNE提取高维空间中的低维流形特征；之后计算样本与参考样本之间的偏离度，并通过多次-最邻近算法分析了不同偏离度计算方法的优劣，然后结合负向转换函数，实现对捷联惯组稳定状态的量化评估；最后通过实例验证了本文所提出方法的有效性。

1 稳定状态评估指标及相关性分析

1.1 捷联惯组的误差系数

捷联惯性测量组合是一种高精度的测量设备，也是惯导系统的核心组件。由于捷联惯组与运载体固连在一起，直接敏感运载体的角运动和线运动，当安装误差或标度误差过大时，将极大地影响到惯导系统的导航精度，因此对捷联惯组进行标定必不可少[7]。对于最常见的动力调谐陀螺捷联惯组而言，通常通过速率标定和位置标定确定捷联惯组误差模型中的33个误差参数，分别为纵向、横向和法向3个通道加速度计的比例系数、零漂和安装误差系数，以及纵向、横向和法向3个通道陀螺仪的零次项漂移、一次项漂移、脉冲当量和安装误差系数，具体误差系数与说明见表1（已省略部分横向、法向通道的的误差系数）。

表1 动力调谐陀螺捷联惯组误差系数说明

Tab.1 SIMU Error Coefficient Description

编号误差系数说 明 1K1x比例系数加速度计纵向通道 2K0x零漂 3Kyx安装误差系数 4Kzx安装误差系数 5K1z比例系数加速度计法向通道 ……… 9K1y比例系数加速度计横向通道 ……… 13D0x零次项漂移陀螺仪纵向通道 14D1x一次项漂移 15D2x一次项漂移 16D3x一次项漂移 17E1x脉冲当量 18Eyx安装误差系数 19Ezx安装误差系数 20D0y零次项漂移陀螺仪法向通道 ……… 27D0z零次项漂移陀螺仪横向通道 ………

1.2 捷联惯组稳定状态指标

1.3 稳定状态指标的相关性分析

相关关系是指两个及两个以上变量的取值表现出一定的规律性[9]。如果能分析33个稳定状态指标的相关性，并采用适当的数据降维方法提取数据中的有效信息、摒弃无用信息，无疑会减少很大的工作量。Pearson相关系数[10]是传统统计学中经典的相关性度量方法，但它只能衡量线性相关性，且存在当变量不符合正态分布时偏差较大、易受异常点的影响等缺点；Reshef等人于2011年在《Science》上发表了论文[11]，研究中通过互信息定义了两个变量之间的最大信息系数（Maximal Information Coefficient，MIC），MIC不仅可以对大量数据中变量间的线性和非线性关系进行度量，而且可以广泛地挖掘出变量间的非函数依赖关系[11,12]。

图1 Pearson相关系数和MIC直方图

从图1中可以看出，只有少数指标对存在极强的相关关系，Pearson线性相关系数的绝对值和MIC值都较大；所有指标对的Pearson线性相关系数的绝对值集中分布在[0，0.2]上，而MIC值集中分布在[0.2，0.4]上，说明指标间的线性相关性要弱于非线性相关性，在进行特征提取时更适合使用非线性的方法。

2 捷联惯组稳定状态评估原理

2.1 捷联惯组稳定状态评估流程

处理同一厂家、同一批次、同一履历的捷联惯组的历次测试数据得到稳定状态评估指标，经过加权后代替欧氏距离计算样本间的条件概率，然后通过加权-SNE算法得到低维空间中的特征指标，再计算各样本与参考样本的偏离度，通过多次-最邻近算法比较不同偏离度计算方法的优劣，最后结合负向转换函数得到捷联惯组的稳定度。其主要流程如图2所示。

图2 捷联惯组稳定状态评估流程

2.2 t-SNE流形学习

在处理高维数据时，数据降维常用于提取有效信息，摒弃无用信息。如按照结构保持方式进行划分，根据降维方法可分为全局信息保持和局部信息保持两大类[13]。流形学习以能够有效揭示出高维数据中的低维本质特征及对特征信息的局部保持性更强而著称，又存在着获取全局分布特征信息性能较差的缺陷。-SNE[14]是由G Hinton于2008年根据2002年Hinton和Rowei所提出的SNE算法[15]进行改进并提出的一种深度学习的非线性流形学习算法，主要用于非线性特征提取和数据可视化，并且得出了-SNE在降维效果上要优于Isomap、Sammon Mapping和LLE的结论。-SNE算法是一种倾向于保留局部特征的非线性降维方法，它最大的特点是能够使高维空间距离较远的点在低维空间距离更远，高维空间距离较近的点在低维空间距离稍小，即数据集衰退域附近所包含的较大曲率流形在低维空间得以保持[16]。

-SNE的算法思想是把高维空间数据点之间的相似性以条件概率的形式来表示，并假设高维空间样本点之间的欧氏距离服从高斯分布，低维空间样本点之间的欧氏距离服从分布，然后通过迭代法使得两个分布的距离最小。其主要算法原理如下：

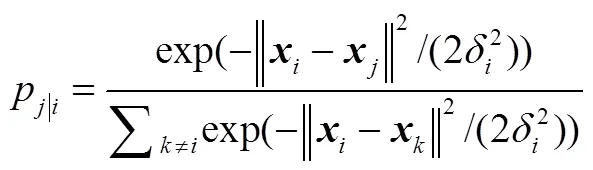
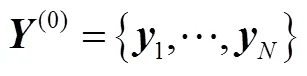
e）更新输出：

f）反复迭代步骤d、步骤e，直到迭代次数满足。

2.3 加权距离

2.3.1 加权距离的定义

-SNE算法将数据的欧氏距离转化为条件概率来表示样本间的相似性，在样本数目和维数都较大的情况下取得了很好的可视化效果，如手写字体识别等。但在捷联惯组的稳定状态评估中，通常难以获得较大的样本数目，指标的维数也有限，且各个指标的量纲、变异系数存在很大不同，仍旧使用欧氏距离转化成条件概率来表示样本间的相似性就不再合适了。因此，本文先对样本间的欧氏距离进行加权再转化为条件概率来表示样本间的相似性，加权距离需要满足以下3个条件：

a）各个稳定状态的指标的重要程度应相等，不受因其量纲不同导致的不可公度的影响；

b）对于稳定状态最佳的参考样本（各项稳定状态指标均为0），样本的各稳定状态指标越大则其与参考样本的加权距离越大，但不因某一指标过大时导致其他指标的大小对加权距离的影响过小；

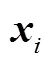
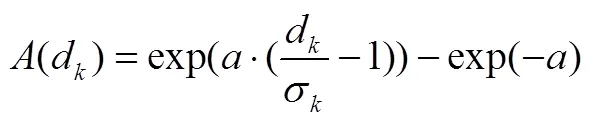
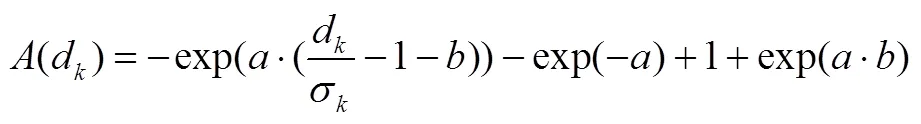
图3为不同、取值下加权函数在定义域内的函数图像，横轴为的值，纵轴为相应的加权函数的值。从图3中可见，加权函数是一个连续且递增函数，其极小值点为（0,0），当趋近于无穷大时，加权函数有极大值；在区间中是一个凹函数，在区间中是一个凸函数。加权函数是一个递增函数，且存在极大值，满足了条件b；加权函数在两侧附近斜率达到最大，使得在任意处有微小增量时，在趋近于时对应的增量和最大，满足了条件c。

2.3.2 基于遗传算法的形状参数的选择

遗传算法（Genetic Algorithm，GA）[17,18]是一种应用广泛的优化搜索算法，能够有效减少陷入局部最优解的风险。取适应度函数为

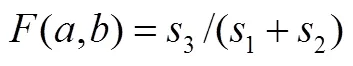
求解参数、的算法原理框图如图4所示。

2.4 偏离度和稳定度

定义偏离度为样本与参考样本的偏离程度。在表示样本间相似程度或偏离程度的方法中，比较常见的是各种距离量度方法，如欧氏距离、马氏距离、曼哈顿距离、DTW距离等。对于使用距离来量度的方法，还需要通过定义稳定度来量化捷联惯组的稳定状态，当样本与参考样本的偏离度趋近于0时，稳定度应趋近于1；当样本与参考样本的偏离度趋近于无穷大时，稳定度应趋近于0。

本文使用负向转换函数，将定义稳定度如下：

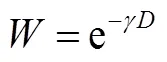
同时，也有一些综合评价方法能够表示样本间的相似性，如用信息的无序度来衡量信息效用值的熵值法[19]和通过比较各比较序列与参考序列间序列曲线几何形状的相似程度来判断序列间的关联程度的灰色关联分析法[20]等。这些综合评价方法的结果直接就在[0,1]的区间内，因此评价结果既可以作为偏离度，也可以直接作为稳定度，无需再通过负向转换函数转换。

2.5 基于K-最近邻算法的偏离度计算方法选择

-最近邻算法（-Nearest Neighbor，KNN）算法是数据挖掘分类技术中最简单有效的方法之一，其基本思路可以介绍如下[21]：针对一个给定的类别标签未知样本，寻找其在训练样本集中的个相似样本, 进而组成近邻集，然后在近邻集上施加最大投票规则，以此确定待识别样本的类别属性。

为分析不同偏离度计算方法的效果好坏，将通过多次KNN分类算法，KNN算法原理如图5所示。

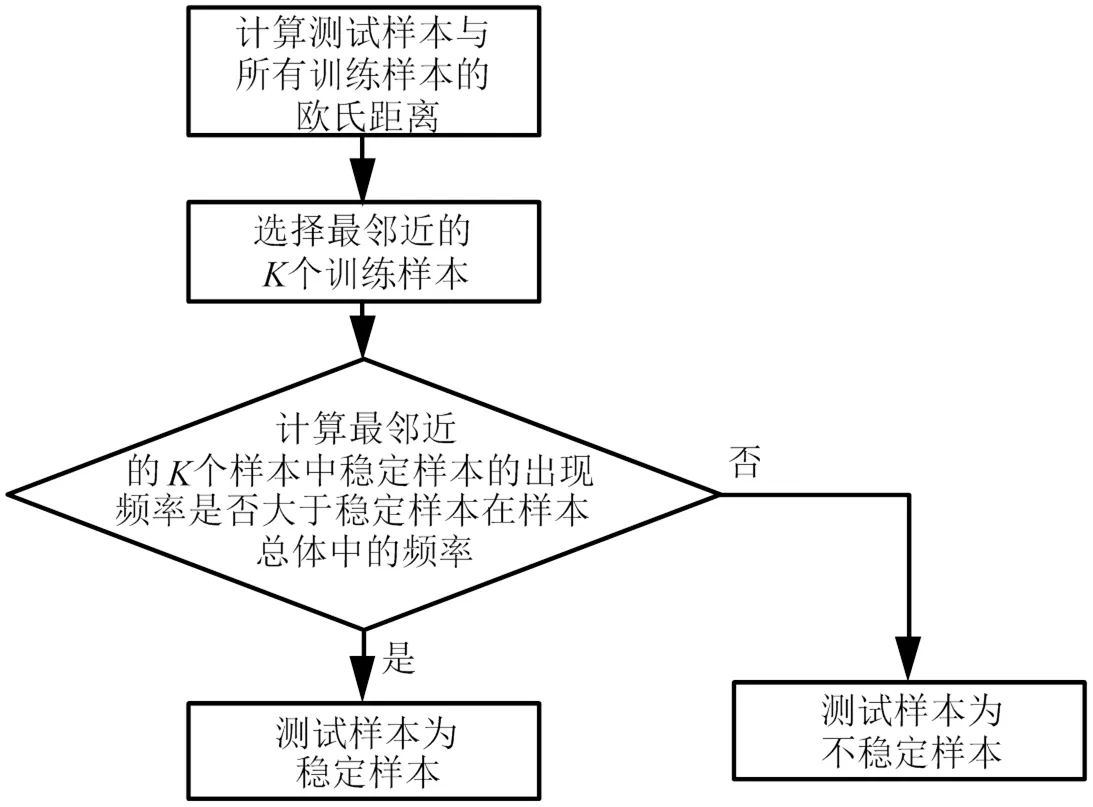
图5 KNN算法原理

比较使用不同偏离度计算方法时的分类平均正确率及其标准差，以此为依据选择最优的偏离度计算方法。由于此时样本仅有偏离度一个属性，因此使用欧氏距离作为相似性比较方法；在投票原则上，由于总样本数量有限且两类样本数量不均匀，需要根据两类样本数量的比例来确定。

3 实例验证

3.1 数据预处理

对16套出产于同一厂家、同一批次且同一履历的某型捷联惯组的历次标定数据进行合格性分析，将部分受标定当地重力加速度影响的误差系数转换到标准重力加速度下，计算同一套惯组两次标定之间误差系数的变化量，经传统稳定性分析共得稳定状态样本84组，不稳定状态样本32组。对各样本编号，其中1~84为稳定样本，85~116为不稳定样本。由于-SNE的降维结果是以迭代的方式产生的，每次降维的结果都不一样，因此每次进行评估时需在样本总体里添加1个各指标都为0的参考样本。

3.2 欧氏距离与加权距离比较

图6a、图6b表示了稳定样本、不稳定样本与参考样本之间的欧氏距离和加权距离分布。显然图6a中两类样本间差异较小，图6b中两类样本的差异较大，且图6a与图6b中各样本与参考样本的距离随样本编号变化的趋势基本一致，说明加权距离能更好地度量样本间的相似程度。

-SNE是一种倾向于保留局部结构的降维方法，为了更多地保留局部信息，设置困惑度为50。为了比较-SNE与加权-SNE两种方法的降维效果，绘制了用这两种方法将稳定性指标降维到2维时的特征分布图，见图6c、图6d。在图6c中，稳定样本与不稳定样本交错分布，说明-SNE不能将两类样本很好地区分开来；在图6d中，不稳定样本分布在稳定样本的外围，且不存在交错分布，区分度明显强于图6c。值得一提的是，捷联惯组是否处于稳定状态主要取决于部分变异系数较大的稳定状态指标是否超出2.7，而从数据特性上分析，各个指标大都符合正态分布，因此各个样本在降至2维时的特征分布不能形成两个类间距离较大、类内距离较小数据点集合，只能形成聚类成两个聚类中心相近、类间距较大的数据点集合。

当使用-SNE将数据集降维至2~3维时，通常不能充分保留样本间的局部结构信息，因此通常需要增加降维维数，本文使用加权-SNE方法对捷联惯组稳定状态数据集降维至6维。

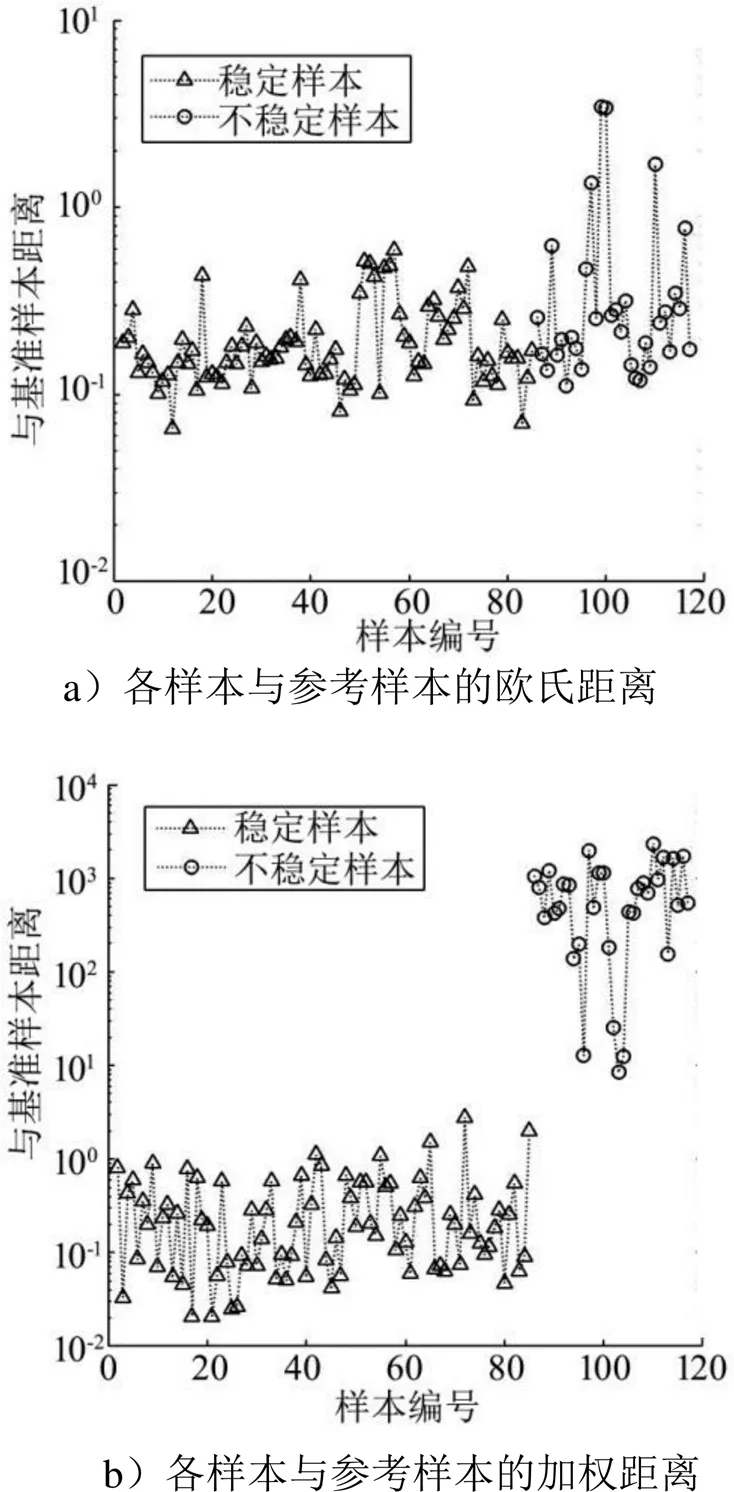
图6 t-SNE与加权t-SNE降维效果对比

3.3 稳定状态评估结果

-SNE降维后结果本身的距离是没有意义的，因为-SNE方法的本质在于降维前后样本间的联合概率分布相等，因此本文使用以下5种常用的方法来计算评估样本与参考样本的偏离度。

表2 偏离度计算方法

Tab.2 Deviation Calculation Method

编号方法特点 1欧氏距离原理简单，应用广泛 2标准化欧氏距离消除了指标量纲的影响 3马氏距离消除了指标间相关性的影响 4熵值法根据信息量对指标赋权，没有主观因素的影响 5熵权-灰色关联分析法根据序列与参考序列间的几何相似程度来衡量样本间的差异，赋权方法客观

考虑到每次使用-SNE降维后的结果都不一样，为了比较不同的度量方法挖掘降维后数据信息的优劣，使用KNN算法分析不同方法度量结果的分类性能。由于两类样本的数量差异较大，首先改进KNN算法，使得KNN在根据个欧氏距离最邻近的样本的类别对测试样本进行分类时，能按照两类样本数目的比例来判断；然后计算50次加权-SNE降维，并将每次提取的低维特征结合这5种方法的评估各样本与参考样本的差异程度；之后对每种方法的评估结果抽取10%的样本作为测试样本，剩余样本作为训练集使用KNN算法并计算分类正确率，重复100次；最后计算取不同值时各评估方法分类的平均正确率和标准差。

图7为不同偏离度计算方法效果对比。在图7中，平均正确率和标准差随的增大呈波浪型变化且变化幅度逐渐缩小，这是由于两类样本的数量不均等，分类结果会根据上文所确定的投票规则倾向于样本数量占总体比重更小的不稳定样本。欧氏距离作为偏离度时其分类的平均正确率最高、标准差最小，说明使用欧氏距离作为偏离度能取得更好的评估效果。

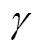
图7 不同偏离度计算方法效果对比

图8 偏离度为欧式距离时的评估结果

4 结 论

高精度捷联惯组是惯导系统的核心组件，其稳定状态决定了其能否被使用。本文提出基于加权-SNE算法和偏离度的方法对捷联惯组的稳定状态进行量化评估，并通过实例验证了该方法的有效性和合理性，说明该方法可以应用于工程实践中。

a）-SNE算法是一种倾向于保留局部特征的非线性降维方法，它能有效提取出捷联惯组稳定状态指标中蕴含的低维流形特征，并通过-长尾分布使相似性高的样本距离更近，相似性低的样本距离更远，准确反映出捷联惯组的稳定性特征；

b）偏离度计算方法多种多样，需经过实例检验才能找到最合适的方法，比如本文中最简单的欧式距离效果比当前应用广泛的马氏距离在分类上效果更好；

c）下一步可以将误差系数的变化量结合基于时间序列的插值与预测技术，扩充单套捷联惯组的样本容量，实现对单套捷联惯组稳定状态长期评估与预测。

[1] 王巍. 新型惯性技术发展及在宇航领域的应用[J]. 红外与激光工程, 2016, 45(3): 11-16.

Wang Wei. Development of new inertial technology and its application in aerospace[J]. Infrared and Laser Engineering, 2016, 45(3): 11-16.

[2] 年夫顺. 关于故障预测与健康管理技术的几点认识[J]. 仪器仪表学报, 2018, 39(8): 1-14.

Nian Fushun. Some understandings about fault prediction and health management technology[J]. Chinese Journal of Scientific Instrument, 2018, 39(8): 1-14.

[3] 彭宇, 刘大同. 数据驱动故障预测和健康管理综述[J]. 仪器仪表学报, 2014, 35(3): 481-495.

Peng Yu, Liu Datong. A review of data driven fault prediction and health management[J]. Chinese Journal of Scientific Instrument, 2014, 35(3): 481-495.

[4] 谷梦瑶, 陈友玲, 王新龙. 多退化变量下基于实时健康度的相似性寿命预测方法[J]. 计算机集成制造系统, 2017, 23(2): 362-372.

Gu Mengyao, Chen Youling, Wang Xinlong. A similarity life prediction method based on real-time health degree under multiple degenerative variables[J]. Computer Integrated Manufacturing Systems, 2017, 23(2): 362-372.

[5] 谷广宇, 刘建敏, 乔新勇. 基于改进-means的发动机状态评估方法[J]. 汽车工程, 2018, 40(7): 844-849.

Gu Guangyu, Liu Jianmin, Qiao Xinyong. An engine state assessment method based on improvedmeans[J]. Automotive Engineering, 2018, 40(7): 844-849.

[6] 赵帅, 黄亦翔, 王浩任, 等. 基于拉普拉斯特征马氏距离的滚珠丝杠健康评估[J]. 机械工程学报, 2017, 53(15): 125-130.

Zhao Shuai, Huang Yixiang, Wang Haoren, et al. A health assessment of ball screws based on laplace's characteristic mahalanobis distance[J]. Journal of Mechanical Engineering, 2017, 53(15):125-130.

[7] 孙伟强, 等. 激光陀螺惯组系统级标定方法[J]. 中国惯性技术学报, 2016, 24(1): 9-13, 25.

Sun Weiqiang, et al. System-level calibration method for laser gyro inertia group[J]. Journal of Chinese Inertial Technology, 2016, 24(1): 9-13, 25.

[8] 张国良, 邓方林, 曾静. SIMU误差系数长途运输影响度量的探讨[J]. 弹箭与制导学报, 2002(S1): 182-185.

Zhang Guoliang, Deng Fanglin, Zeng Jing. Discussion on the influence measure of long-distance transportation of SIMU error coefficient[J]. Journal of Projectiles, Rockets and Guidance, 2002(S1): 182-185.

[9] 唐小川. 大数据相关关系挖掘的若干关键问题研究[D]. 成都: 电子科技大学, 2018.

Tang Xiaochuan. Research on some key issues of big data correlation mining [D]. Chengdu: University of Electronic Science and Technology, 2018.

[10] Kononenko I. Estimating attributes: analysis and extensions of RELIEF[M]// Machine Learning: ECML-94. Heidelberg: Springer Berlin Heidelberg, 1994.

[11] Reshef D N, et al. Detecting novel associations in large data sets[J]. Science, 2011, 334 (6062): 1518-1524.

[12] 梁吉业, 冯晨娇, 宋鹏. 大数据相关分析综述[J]. 计算机学报, 2016, 39(1): 1-18.

Liang Jiye, Feng Chenjiao, Song Peng. A review of big data correlation analysis[J]. Chinese Journal of Computers, 2016, 39(1): 1-18.

[13] 赵孝礼, 赵荣珍. 全局与局部判别信息融合的转子故障数据集降维方法研究[J]. 自动化学报, 2017, 43(4): 560-567.

Zhao Xiaoli, Zhao Rongzhen. Research on dimensionality reduction method of rotor fault data set based on global and local discriminant information fusion[J]. Acta Automatica Sinica, 2017, 43(4): 560-567.

[14] Hinton G E. Visualizing high-dimensional data using t-SNE[J]. Vigiliae Christianae, 2008, 9(2): 2579-2605.

[15] Hinton G, Roweis S. Stochastic neighbor embedding[J]. Advances in Neural Information Processing Systems, 2003, 15(4): 833-840.

[16] 张康, 等. 基于-SNE数据驱动模型的盾构装备刀盘健康评估[J/OL].机械工程学报: 1-8[2019-04-22]. http://kns.cnki.net/kcms/detail/11.2187.TH.

20190124.1320.072.html.

Zhang Kang, et al. Health assessment of shield equipment based on t-SNE data driven model[J/OL]. Journal of Mechanical Engineering: 1-8 [2019-04-22]. http://kns. cnki.net/kcms/detail/11.2187.TH.20190124.1320.072.html.

[17] Tang K S, et al. Genetic algorithms and their applications[J]. IEEE signal processing magazine, 1996, 13 (6): 22-37.

[18] 苏亮, 等. 循环遗传聚类法稳定图自动分析[J]. 浙江大学学报(工学版), 2017, 51(3): 514-523.

Su Liang, et al. Automatic analysis of stability graphs in cyclic genetic clustering[J]. Journal of Zhejiang University (Engineering Science), 2017, 51(3): 514-523.

[19] 朱喜安, 魏国栋. 熵值法中无量纲化方法优良标准的探讨[J]. 统计与决策, 2015(2): 12-15.

Zhu Xi'an, Wei Guodong. Discussion on the excellent standard of the dimensionless method in entropy method[J]. Statistics & Decision, 2015(2): 12-15.

[20] 罗毅, 李昱龙. 基于熵权法和灰色关联分析法的输电网规划方案综合决策[J]. 电网技术, 2013, 37(1): 77-81.

Luo Yi, Li Xiaolong. Comprehensive decision-making of transmission network planning scheme based on entropy weight method and grey relational analysis method[J]. Power Grid Technology, 2013, 37(1): 77-81.

[21] 葛江华, 刘奇, 王亚萍, 许迪, 卫芬. 支持张量机与KNN-AMDM决策融合的齿轮箱故障诊断方法[J]. 振动工程学报, 2018, 31(6): 1093-1101.

Ge Jianghua, Liu Qi, Wang Yaping, Xu Di, Wei Fen. A gearbox fault diagnosis method supporting the combination of tensor and KNN-AMDM decision making[J]. Journal of Vibration Engineering, 2018, 31(6): 1093-1101.

Stable State Estimation Method of SIMU Based on Weighted-SNE andDegree of Deviation

Li Ya, Xu Jun-hui, Shan Bin, Zhen Zhan-chang

(Rocket Force Engineering University, Xi’an, 710025）

Aiming at the shortcomings of the traditional strapdown inertial navigation system(SIMU) stability analysis method, which can only be qualitatively evaluated and cannot be quantified and compared, a method is proposd based on the data-driven method to extract the data from the manifold learning method embedded in the t-distribution domain. Dimensional manifold characteristics, and then calculate the deviation of each sample from the reference sample to evaluate the steady state of the SIMU. In the example verification, the dimensionality reduction effect of ordinary t-SNE and weighted t-SNE are compared, and the Euclidean distance, standard Euclidean distance, Mahalanobis distance, entropy method and entropy weight-Gray correlation analysis method are analyzed by K nearest neighbor classification algorithm. The evaluation results of the five commonly used deviation calculation methods prove the effectiveness of the proposed method.

SIMU; state evaluation; manifold learning;-SNE; weighting; degree of deviation

TP202+.1

A

1004-7182(2020)02-0064-08

10.7654/j.issn.1004-7182.20200213

李 亚（1995-），男，硕士研究生，主要研究方向为惯性器件测试及状态评估技术。

徐军辉（1974-），男，副教授，主要研究方向为惯性技术、小样本建模理论。

单 斌（1974-），男，副教授，主要研究方向为惯性技术测试技术、惯性导航。

甄占昌（1966-），男，高级工程师，主要研究方向为惯性测量组合测试技术。

2019-06-01；

2019-09-19