输电线工程中双钢管杆结构优化设计分析

梁东跃 李兆峰 肖俊俊 王向阳 邹本为

（1.安徽华电工程咨询设计有限公司，合肥230022；2合肥工业大学土木与水利学院工程力学系，合肥230009）

0 引 言

随着我国经济的快速发展，国家城镇化战略的推进，电力行业也得到了飞速发展。由于电压等级的提高和输电载荷的增大，加之多种输电线路交叉混合，对输电线结构的性能要求越来越高，而随着土地资源的开发，对常规输电线结构的占地面积在却不断压缩，先前单一结构的输电塔已很难满足实际需求，迫切需要新型的大型组合特种结构输电线塔用于当前的电力建设领域。通常情况下，一种新型的组合结构从研发到逐渐推广应用需要进行大量的理论支撑和试验分析，这些研究一般主要注重于结构的承载性能，因此一般的新型组合结构会有较大的安全裕度，这就导致了结构的经济性不佳，而输电线塔作为电力建设中重要承重载体，其工程体量是巨大的。因此，对输电线塔的组合结构进行优化设计研究具有可观的经济效益和国家战略意义。肖勤等［1］基于满应力准则法，以直线塔的塔身坡度为设计变量，对输电塔进行了结构优化设计。Aydoğdu［2］和Talebpou等［3］基于蚁群算法采用离散变量的方法对输电塔结构进行了优化设计，表现出了良好的经济性能。郭惠勇等［4］基于人工鱼群算法，改进了视野和步长的变化策略以及觅食行为的加速策略，针对输电塔塔腿进行了拓补优化，表现出了良好的优化效率。Sivakumar［5］以及郭惠勇等［6］基于遗传算法采用离散变量的方法针对输电塔结构的形状以及各杆件截面尺寸进行了优化。武岳［7］和罗正帮等［8］基于萤火虫算法以结构的刚度、强度以及稳定性为控制变量，以结构的重量为优化目标对输电塔等杆系结构的截面尺寸进行了优化设计，充分利用了各杆件的力学性能。张卓群等［9］基于蚁群算法对高压输电塔进行局部结构优化设计。

本文基于萤火虫优化算法（firefly algorithm），以双钢管杆结构各类主要构件的管径和壁厚为设计变量，以整体结构和各连接处的承载性能为约束条件，对整体结构进行优化分析分析，为类似工程提供参考。

1 萤火虫优化算法

萤火虫算法（FA）是近些年来最新提出的一种群智能优化算法。在2008年，剑桥学者Yang［10］提出了FA 算法。该算法的基本思想是萤火虫被绝对亮度比它大的萤火虫所吸引，并根据位置更新自身位置。在人工萤火虫群优化算法中，每只萤火虫作为自变量，随机分布在搜索区域内，每只萤火虫在各自的邻域内搜寻，会被亮度较强的萤火虫所吸引或吸引亮度较弱的萤火虫，最终使得萤火虫聚集到亮度较强的萤火虫周围，也即是找到多个极值点，从而达到优化的目的。萤火虫算法相比其他群智能优化算法具有收敛速度快、全局寻优效果好（避免了其他算法早熟收敛现象）以及精度高等特点，适合于复杂情况下的优化［11］。基于萤火虫算法的不断改进与完善，此优化方法也用于数字图像处理、电力、土木工程结构等领域。

1.1 萤火虫优化算法理论

萤火虫算法包含两个重要因素:亮度和吸引度。其中，亮度决定了萤火虫所处位置的优劣并决定移动方向，吸引度决定了移动距离。萤火虫绝对亮度Ii即为某只萤火虫i的初始光亮度。萤火虫相对亮度Iij即为萤火虫i在萤火虫j所在位置产生的光亮度。吸引力βij即为萤火虫i对萤火虫j的吸引力。

在优化问题中，假定萤火虫i的绝对亮度等于目标函数值，即

式中，xi为萤火虫位置向量，在优化中体现为多个变量。

萤火虫相对亮度为

式中:rij为萤火虫i到萤火虫j的距离；γ为光吸收系数，代表了吸引力的变化，一般取为0～1。

萤火虫吸引力为

式中:β0为萤火虫i在光源处的吸引力，一般取1；rij为萤火虫i到萤火虫j的笛卡尔距离，表达式为

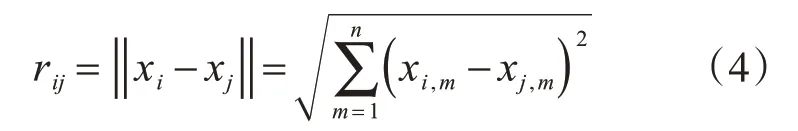
式中:xi为萤火虫坐标；m为求解问题的空间维度；xi'm为第i个萤火虫在m维的坐标。

由于萤火虫j被萤火虫i吸引，其位置就会不断更新，坐标更新公式为

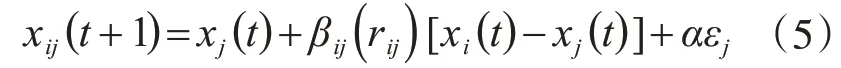
其中，t为算法迭代次数；α为步长因子；εj为随机因子。坐标更新公式等号右侧的第二项为因吸引力产生的距离，第三项为随机移动的距离。

1.2 萤火虫优化算法数学模型

将萤火虫优化算法应用于工程实际项目中，就必须针对该项目的具体特点建立相应的优化数学模型。对于输电线钢管杆组合结构优化设计，要遵循电力行业设计规范规程［12-15］的相关要求，要保证优化之后的输电线钢管杆组合结构的承载性能依然稳定可靠，在满足结构强度、刚度、稳定性等约束条件的前提下，对优化后的组合结构的各类承载性能指标进行复查和校核，从而保证结构的安全性和可靠性。

本研究的优化目的是在保证结构正常运行的状况下，对结构各构件的布局和截面尺寸进行调整或减小，以达到减轻结构重量，减少材料消耗的目的。基于萤火虫算法的输电线钢管杆结构优化设计的具体优化数学模型如下:

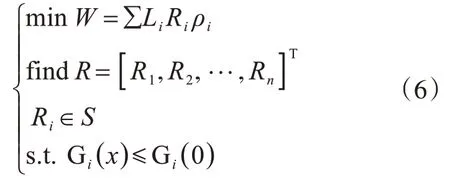
式中:W为输电塔总重量；Li为杆件长度；Ri为杆件截面半径；ρi为材料密度；R1-Rn为设计变量；S为设计变量的取值范围；Gi(x)为结构的可靠性指标计算值；G(0)为结构的可靠性指标容许值，在双杆钢管杆中表现为umax＜[u]，σmax＜[σ]，umax为钢管杆最大位移值；[u]为挠度限值，依据规范［13］第6.2 节规定钢管杆塔在长期荷载作用下位移限值为 15 h/1 000；σmax为钢管杆最大 Mises 应力值；[σ]为钢材构件应力设计强度，对于Q420 钢材，强度设计值为380 MPa。

以钢管杆各构件截面尺寸为设计变量，根据优化表达式（6），使用MATLAB 编写萤火虫算法程序。对钢管杆结构建立力学分析模型，采用有限元法壳单元建立有限元法分析模型，调用有限元法进行力学分析，然后用萤火虫优化算法进行结构优化迭代，优化流程见图1。

2 双钢管杆结构优化设计分析

2.1 工程概况

以某一110 kV 混压输电双钢管杆SSFG2 为研究对象，主杆截面为十六边形，分为7 段，稍径为850 mm，根径为1 900 mm，两主杆之间的中心距为3.2 m，总高度为62.5 m，呼高27 m，其结构形式如图2 所示。该杆型预留220 kV 导线横担，导线安全系数为8（最大使用张力分别为16 370 N和35 314 N），地线安全系数为10（最大使用张力分别为3 307 N 和9 062 N）。主体结构采用Q420钢，局部采用Q345钢，钢管杆总质量88 663 kg。

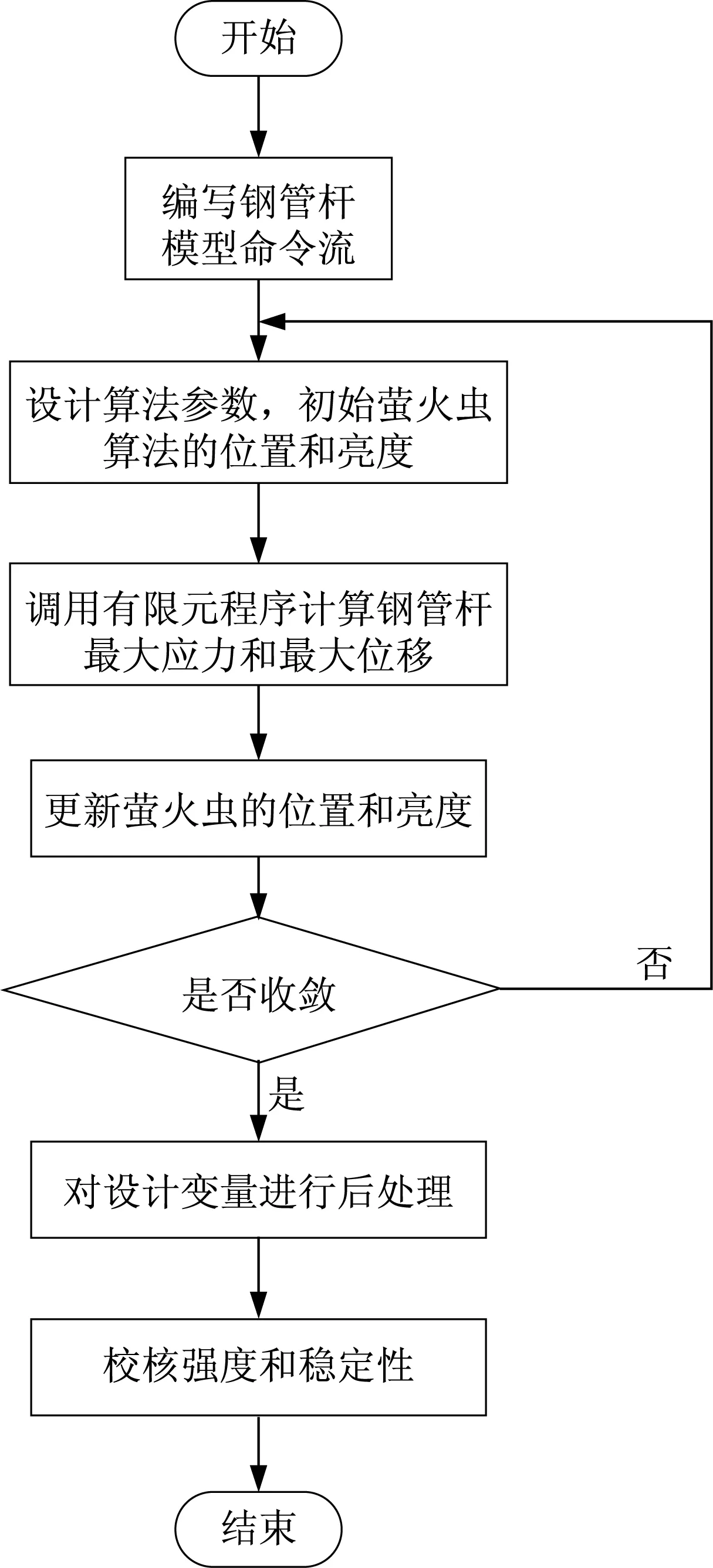
图1 结构优化流程图Fig.1 Flow diagram of structural optimum

2.2 基本荷载与工况

双钢管杆结构设计荷载主要可分为两部分:第一部分是钢管杆自身载荷，即自重；第二部分是钢管杆所承受的外部荷载作用，包括风载、雪载、覆冰荷载及导线对钢管杆的作用。由于自身的雪荷载对钢管杆整体结构受力影响较小，因而忽略雪荷载对钢管杆的影响。钢管杆设计阶段荷载工况见表1 所列。外部荷载包含的风荷载、覆冰荷载和导线对钢管杆的作用统一进行考虑并给出，采用节点集中载荷的形式施加在钢管杆结构模型节点上。考虑到工况众多，故采取控制工况进行结构优化。

2.3 双钢管杆结构力学模型

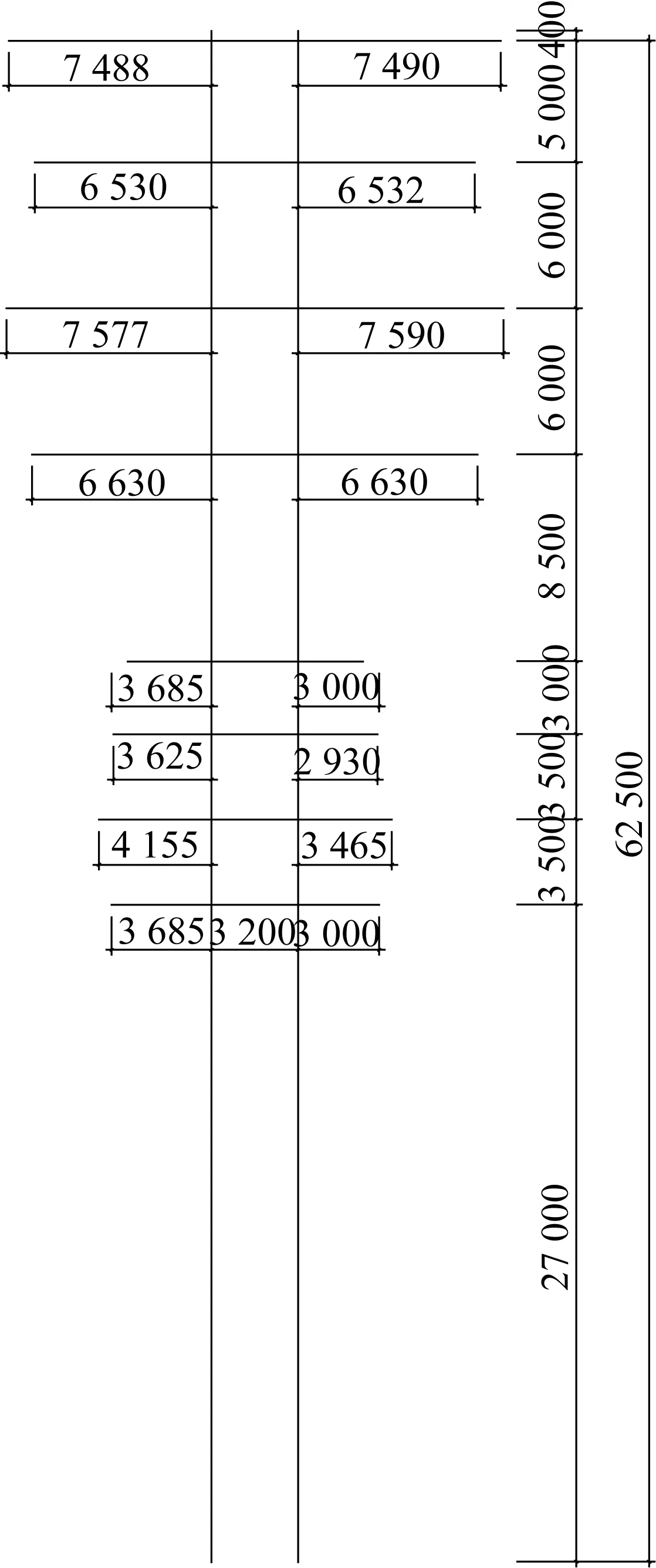
图2 SSFG2立面图（mm）Fig.2 Elevation of tower SSFG2（Unit:mm）

表1 SSFG2荷载工况Table 1 Load case of tower SSFG2

双钢管杆由2根主杆（每根主杆分为7段）、16根横担以及8 根连接杆组成，主杆与主杆、主杆与横担、主杆与连接杆之间的连接均采用刚性法兰连接，见图3，故将此处连接视为刚接，2 根主杆底部均采用固定约束。考虑双钢管杆结构的实际构造和受力特点，以及优化算法中设计变量的特点，因此钢管杆整体结构的各构件均采用四边形四节点壳单元模拟，整体结构有限元模型共计40 883个单元、40 969 个节点。在钢管杆结构优化分析过程中，整体结构有限元模型可忽略主杆与连接杆、横担之间的法兰盘连接细节。

图3 法兰连接示意图Fig.3 Flange connection

2.4 双钢管杆结构优化设计变量

此次优化分析主要目标是结构自重，而钢管杆结构主要由主杆、连接杆和横担三类主要构件和爬梯、螺栓等部件组成，主要构件的重量超过结构总重量的90%，对所有主要构件进行截面参数优化分析即可达到减轻整体结构自重的目标，并且萤火虫算法可以同时优化多个设计变量。因此，针对钢管杆主杆正十六边形截面的半径以及主杆、连接杆和横担的管径壁厚进行优化，其中8个正十六边形边半径（截面直径为两平行边中轴之间的距离）设为R1～R8，7 段主杆的壁厚设为t1～t7，横担的壁厚设为t8～t10，连接杆的壁厚设为t11～t18，共计 26 个设计变量。在优化过程中，先将设计变量作为连续变量进行优化，然后对优化后的结果参数进行离散化处理。选取SSFG2钢管杆各类型设计变量的初始值以及其定义域的代表值进行汇总，其中主杆半径取R1和R8，主杆壁厚取t1和t7，横担壁厚取t8，连接杆壁厚取t11和t18，如表2所示。

3 双钢管杆结构优化结果分析

设定双钢管杆SSFG2萤火虫优化算法的种群为50，代数为200，即该结构进行约800 次有限元迭代分析，得到优化结果，优化设计历程如图4 所示。SSFG2在长期荷载工况下的初始值与优化值的对比见表3。将优化后的构件截面结果代入整体结构梁单元模型进行有限元法验证分析，优化前后各主要构件最大Mises 应力见表4，整体结构顶部最大位移的对比见表5。

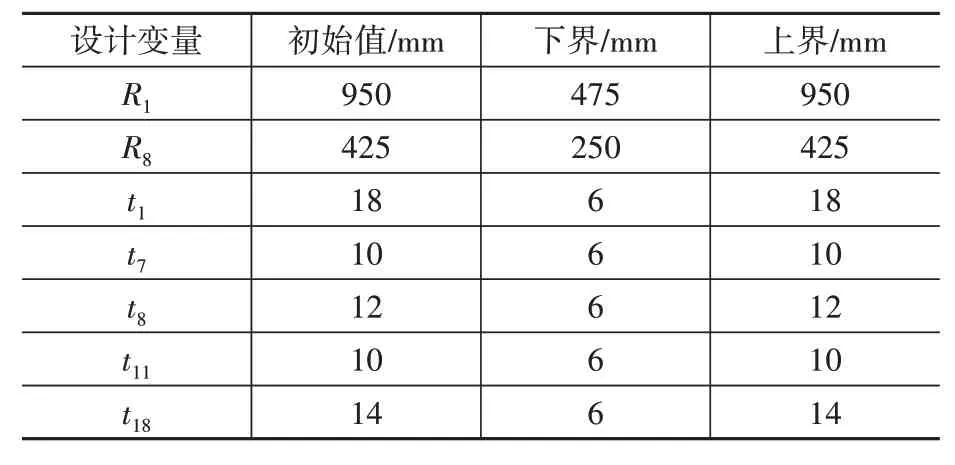
表2 SSFG2结构优化的设计变量Table 2 Variables of structural optimization design of tower SSFG2

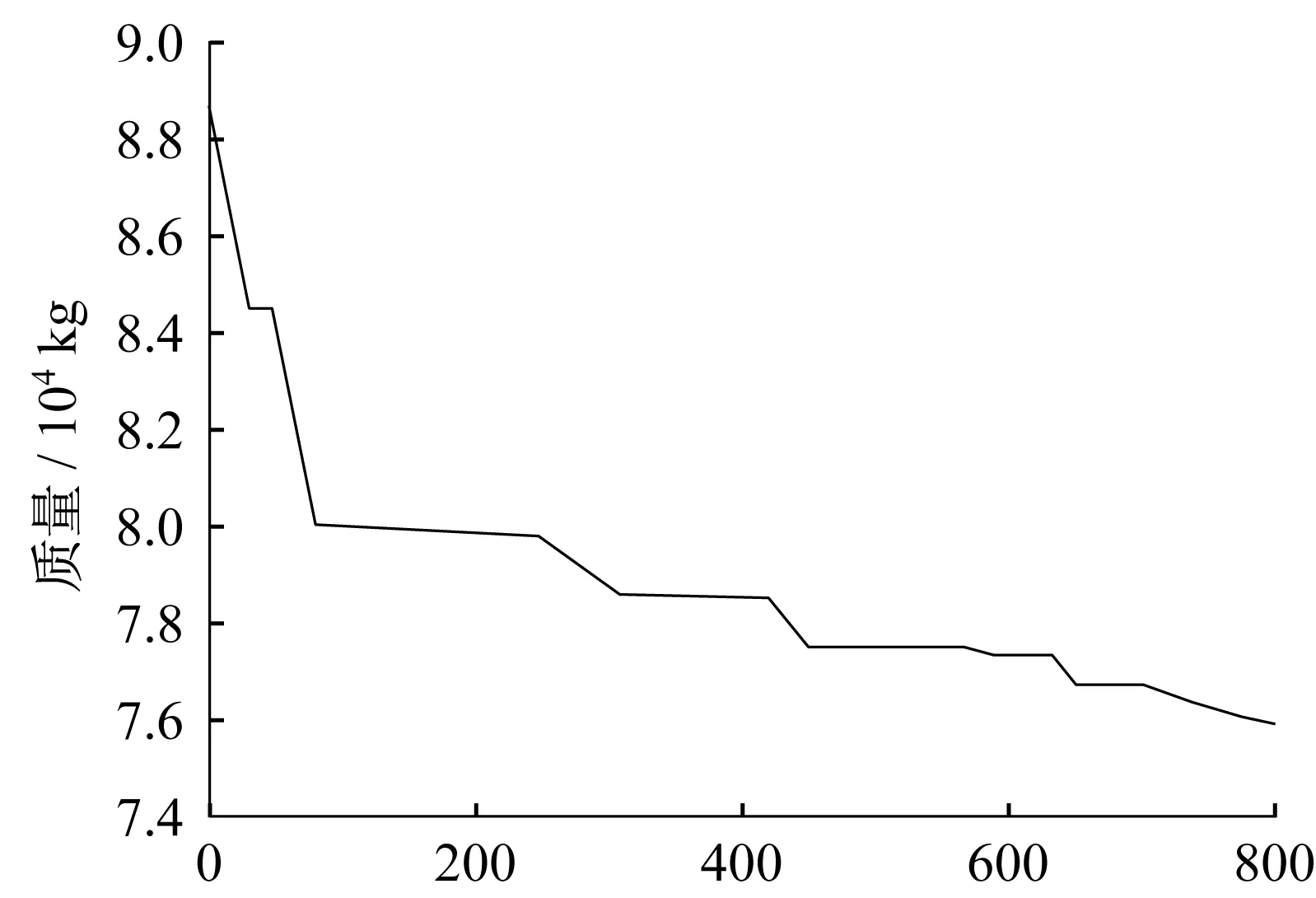
图4 SSFG2结构优化设计历程Fig.4 Optimal design history of tower SSFG2

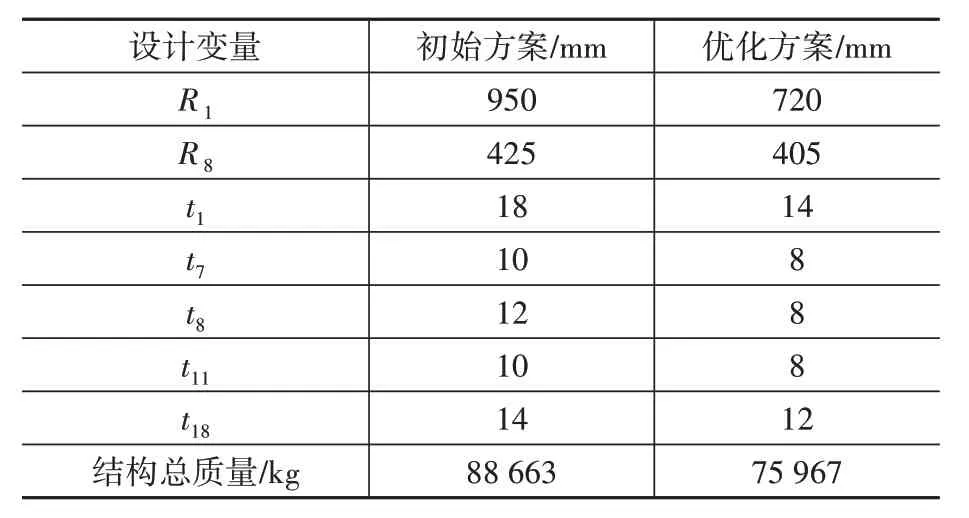
表3 SSFG2结构设计变量优化结果Table 3 Design variable optimal results of tower SSFG2

通过萤火虫算法对SSFG2双钢管杆结构局部构件的截面尺寸进行优化设计，并对优化后的双钢管杆整体结构进行承载性能力学分析和强度与刚度校核，得出结论如下:

（1）由表3 可知，8 个主杆管径半径的最大优化量为24.3%，位于杆最底部一段，最小优化量为4.9%，位于杆最顶部一段，16 个主要构件壁厚分别优化了1～2 个模数（每个模数为2 mm）。优化采用初始方案设计的SSFG2 整体结构质量为88 663 kg，经过构件截面尺寸优化设计后，SSFG2整体结构的质量下降到75 967 kg，经过优化之后的SSFG2双钢管杆整体结构质量较优化前减轻了约14.3%。

表4 SSFG2结构优化前后最大Mises应力Table 4 Comparison of maximum mises stress of tower SSFG2 before and after optimal design（Unit:MPa）

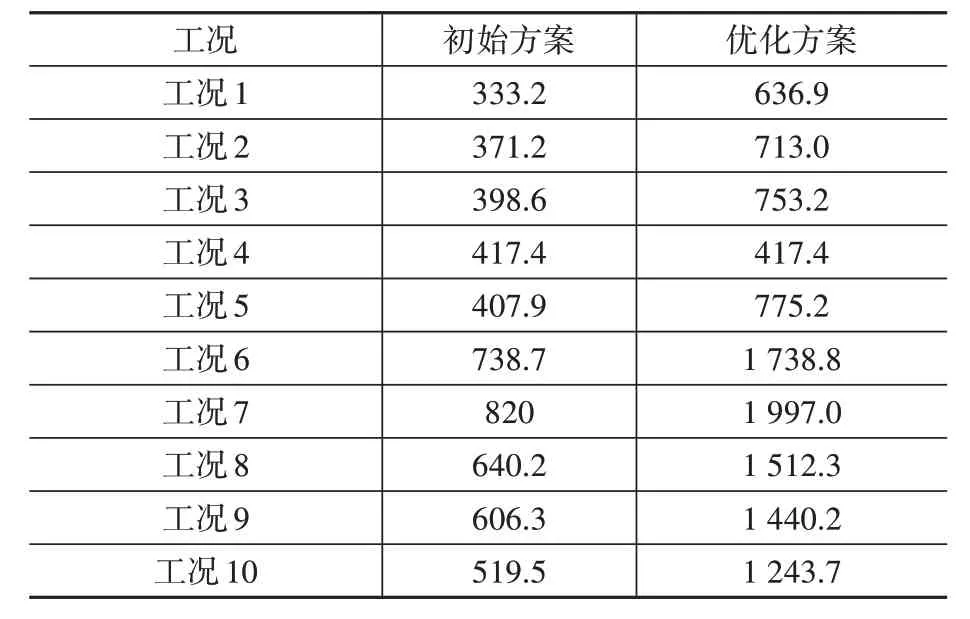
表5 SSFG2结构优化前后结构顶部最大位移Table 5 Comparison of maximum displacement at the top of tower ssfg2 before and after optimal design（Unit:mm）

（2）由表4可知，优化后各工况下整体结构的最大Mises 应力值较优化前增加40%～60%，最不利工况下的最大Mises 应力值为335.4 MPa，均未超过Q420 钢材的许用应力380 MPa，可认为经过优化之后SSFG2双钢管杆整体结构的强度满足设计要求。

（3）各设计工况下的最大Mises 应力值未达到约束条件设定的材料屈服强度，这是由于优化迭代过程中的设计变量是按连续变量考虑，而优化后的设计变量根据钢管制造便利，均取整模数，因此优化后的构件截面尺寸尚有一定的安全裕度。

（4）由表5可知，优化后长期荷载工况下双钢管杆顶部的最大位移（X，Y，Z方向的位移平方和开方）由初始值333.2 mm 增加到636.9 mm，参考《架空送电线路钢管杆设计技术规定》（DL/T 5130—2001）第6.2.1 条关于结构顶部最大位移限值为20h/1 000（h为塔身高度）的要求，即636.9 mm＜20×62.8 m/1 000=1256 mm，说明经过优化之后SSFG2 双钢管杆结构的最大位移值满足规范要求。

综上所述，优化后SSFG2 双钢管杆结构在设计工况下各类构件的最大应力均小于材料的设计强度，且塔顶最大位移值满足要求，SSFG2双钢管杆整体结构的承载性能满足设计要求；经过优化之后的SSFG2双钢管杆整体结构质量较优化前减轻了约14.3%，达到节约制造成本的目标。

4 结 论

本文基于高压输电线钢管杆结构优化设计多变量、多类型约束的特点，利用萤火虫算法收敛速度快、全局寻优效果好以及精度高等特点，对高压输电线钢管杆结构进行了优化设计。结论如下:

（1）SSFG2 双钢管杆经过优化设计后结构整体质量减轻了约14.3%。考虑到整条输电线工程有不少此类结构，因此本文对双钢管杆的优化设计方案具有良好的经济效益。

（2）对优化后的输电线杆结构进行局部构件和整体结构的承载性能进行校核，其优化后的结果满足设计的强度、刚度和稳定性要求，优化后的设计变量满足相关设计参数要求。

（3）对于壳单元为主的双钢管杆结构，以主杆、连接杆以及横担的管径和壁厚共26 个截面参数为设计变量，以整体结构顶部最大位移和各杆件连接处的最大Mises 应力为约束条件；针对上述多个设计变量、多种约束条件的大型组合结构，成功将萤火虫优化算法应用于此类工程的整体结构优化设计，为类似工程设计提供参考。