跨海桥梁大尺寸承台波浪力数值模拟研究

董伟良，诸裕良，胡金春 ，邵 杰,

(1.浙江省水利河口研究院 浙江省河口海岸重点实验室，杭州 310020；2.河海大学 港口海岸与近海工程学院，南京 210098)

大型跨海桥梁正逐渐成为我国沿海主要城市、地区紧密联系的重要通道[1-4]。常处于大风浪条件下的跨海大桥，在设计时必须考虑波浪荷载，而由桩基、承台和墩身组成的跨海桥梁下部结构，波浪荷载计算十分复杂。目前桩基水平力一般直接采用小尺度结构物适用的Morison 公式计算，中、美、英规范均采用该公式[5]。承台因其尺寸相对较大，如鱼山石化疏港公路主通航孔主墩，100 a一遇设计波浪对应的波长仅是承台长度(含防撞设施)的1.35倍，Morison 公式已不适用。

大尺寸承台影响入射波浪场，继而影响承台本身受力情况。现有研究成果主要是在绕射理论基础上对结构波浪力进行理论分析和数值计算，MacCamy-Fuchs线性绕射理论至今得到广泛应用，我国《港口与航道水文规范》(JTS 145-2015)基于该绕射理论给出了大尺寸圆形墩柱一次近似解。张胡[6]以线性波浪绕射理论为基础，建立了大尺度结构波浪力三维数学模型，研究了大尺度结构波浪力。邓莎莎[7]基于绕射理论研究了大尺度桥墩波浪力计算方法。姚文伟[8]利用Garrett线性势流理论采用Matlab编程，研究了有限水深及线性规则波作用下固定不动的圆台垂向作用力变化规律。目前承台波浪力研究大多针对静水位在承台顶底高程之间的情况，而张家玮[9]研究跨海桥梁箱梁结构波浪力时发现，不同淹没条件下箱梁结构受力情况不同。当水位高于承台顶时，较大波浪与承台作用时会伴随波浪冲击、变形和破碎现象，绕射理论不再适用。

近年来数值模拟己逐渐成为研究波浪和结构物相互作用问题的一种重要方法，目前基于N-S方程的波浪力计算方法得到了快速发展，刘桦[10]、郐艳荣[11]、刘浪[12]等人分别利用数值波浪水槽开展了群桩承台复合结构波浪力研究，研究结果表明数值计算方法具有很高的可信度。本文基于Fluent软件建立三维数值波浪水槽，开展了大尺寸桥墩承台波浪力数值模拟试验研究，分析波高、淹没系数、波周期以及承台长度对承台波浪力影响，为跨海大桥桥墩设计建造提供参考。

1 模型建立

1.1 控制方程

采用 Navier-Stokes 方程作为流体运动的控制方程，其连续性方程和动量方程为

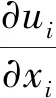
(1)

(2)

式中：ρ是流体的密度；ui为各方向的速度分量，i=1，2，3；P为压强；v是粘性系数；Si为各方向的动量；gi为各方向的重力加速度，这里取g3=9.81 m/s2。紊流模型采用标准k-ε模型。

水面捕捉采用VOF模型，输运方程为

(3)

式中：体积分数函数αq定义为单元内第q相流体所占有体积与该单元的体积之比。

1.2 边界造波法

对于波浪模拟，通过给定入口边界的流速及波高历时变化来进行造波，根据Stokes波理论，入射边界处的水平速度、垂向速度和水深表示为

(4)

(5)

(6)

式中：H、k、d、T分别为波浪波高、波数、静水深和周期。

1.3 消波措施

在数值波浪水槽中设置阻尼层，使波浪在阻尼层内衰减，从而消除反射波。在计算区域末端前设置2～3倍波长的阻尼层消波段，利用 Fluent的DEFINE_SOURCE宏编程可实现消波源项的添加。阻尼层内动量方程中源项和衰减系数分别取如下形式

Si=Deui

(7)

(8)

式中：x0为阻尼层的起点横坐标；x1为阻尼层的终点横坐标；xL为阻尼层内任意点的横坐标。

1.4 求解策略及网格划分

控制方程采用有限体积法进行离散，对流项求解采用二阶迎风格式。采用 PISO 算法求解速度和压力。造波边界采用速度边界，两侧边界采用对称边界，底部采用零滑移壁面边界，上部与空气接触的边界采用压力出口条件。计算区域网格采用棱柱体和四面体网格进行划分，在承台和水面波动范围加密处理。水平向网格取波长的1/50，以实现稳定波浪的生成，波高范围内垂向分为20个网格，结构物中心置于距离入射边界超过3倍波长的位置，距离平行波流传播的两侧固壁边界至少3倍结构特征长度，以减小固壁边界的影响。

2 模型验证

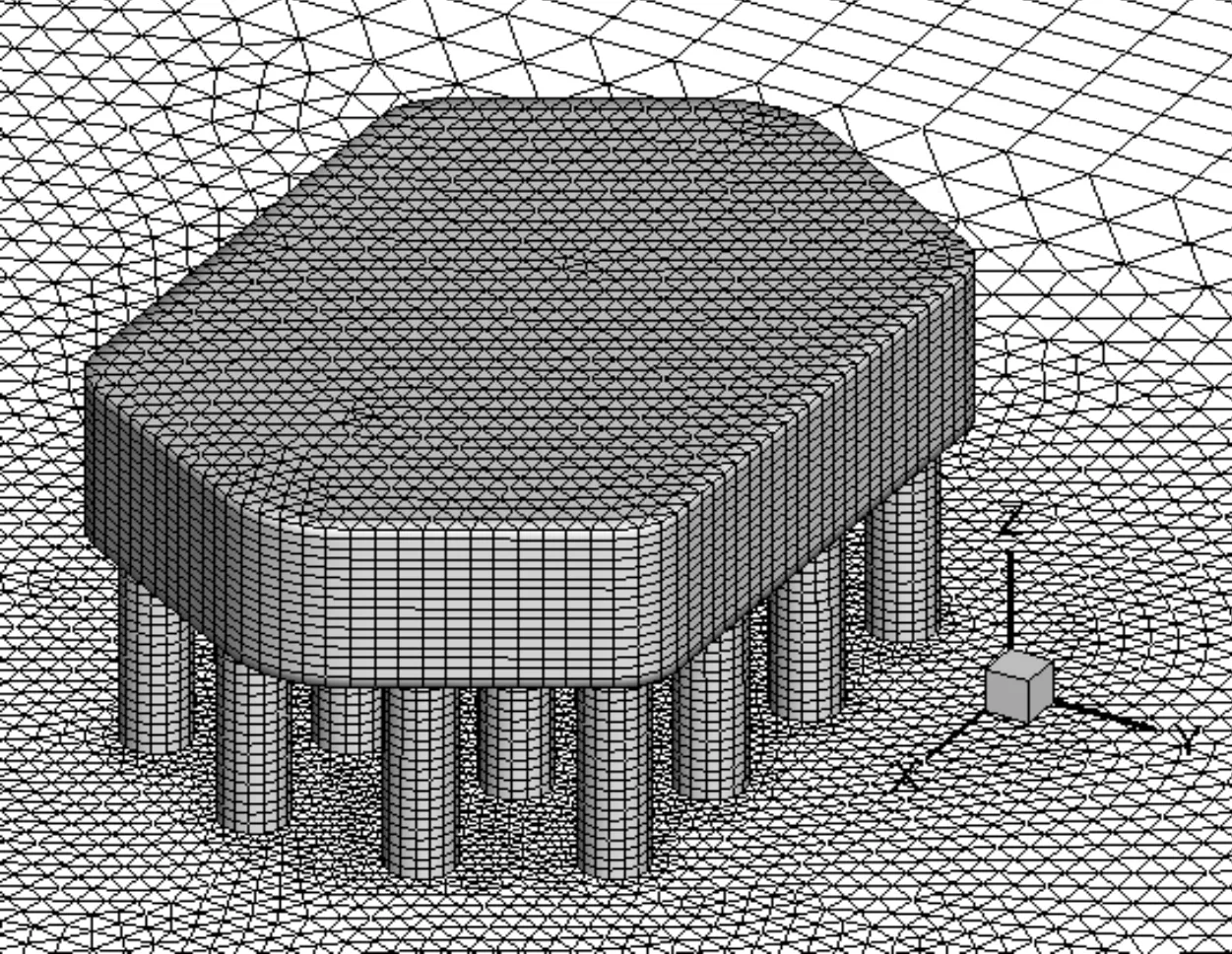
图1 桥墩下部结构尺寸和三维模型Fig.1 Substructure of cross-sea bridge and model of pier

本文数学模型验证主要包括波浪模型验证和波浪-承台相互作用模型验证。选取宁波舟山港主通道(鱼山石化疏港公路)跨海桥梁桥墩物理模型试验成果[13]作为本文验证对象，试验结构包括承台和桩基两部分，试验在浙江省水利河口研究院六堡试验基地的波流宽水槽中进行，水槽长50 m，宽7.0 m，高1.2 m。南通航孔桥墩各向对应的100 a一遇波浪要素为：横桥向，波高H=6.5 m、周期T=8.3 s；顺桥向，波高H=3.84 m、周期T=13.5 s。承台横截面为六边形，桥墩模型示意图见图1。计算域长1 000 m，宽200 m，高40 m。

在波浪模型验证部分，选取横桥向和顺桥向设计波要素进行验证，图2中给出了相同波浪条件下时程曲线的解析结果与数值结果，从图中可以看出，本文数学模型与解析结果几乎完全重合，说明本文数值波浪水槽精度较高。

在波浪-承台相互作用模型验证部分，横桥向和顺桥向不同水位条件下数值模拟计算值和物理模型试验值对比结果见图3，从图中可以看出承台水平力和垂向力数值模拟计算值和物理模型试验值基本一致，误差较小，横桥向和顺桥向水平力最大相对误差分别为11.18%和7.16%，垂向力最大相对误差分别为6.15%和5.74%，总体而言，本文所建立的数学模型能够很好地模拟波浪和桥墩相互作用的过程，可用于下文大尺寸承台波浪力数值模拟研究。

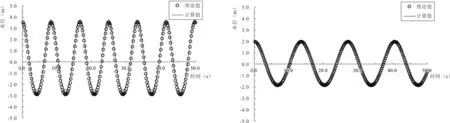
图2 波面时程曲线Fig.2 Variation in free water surface with time

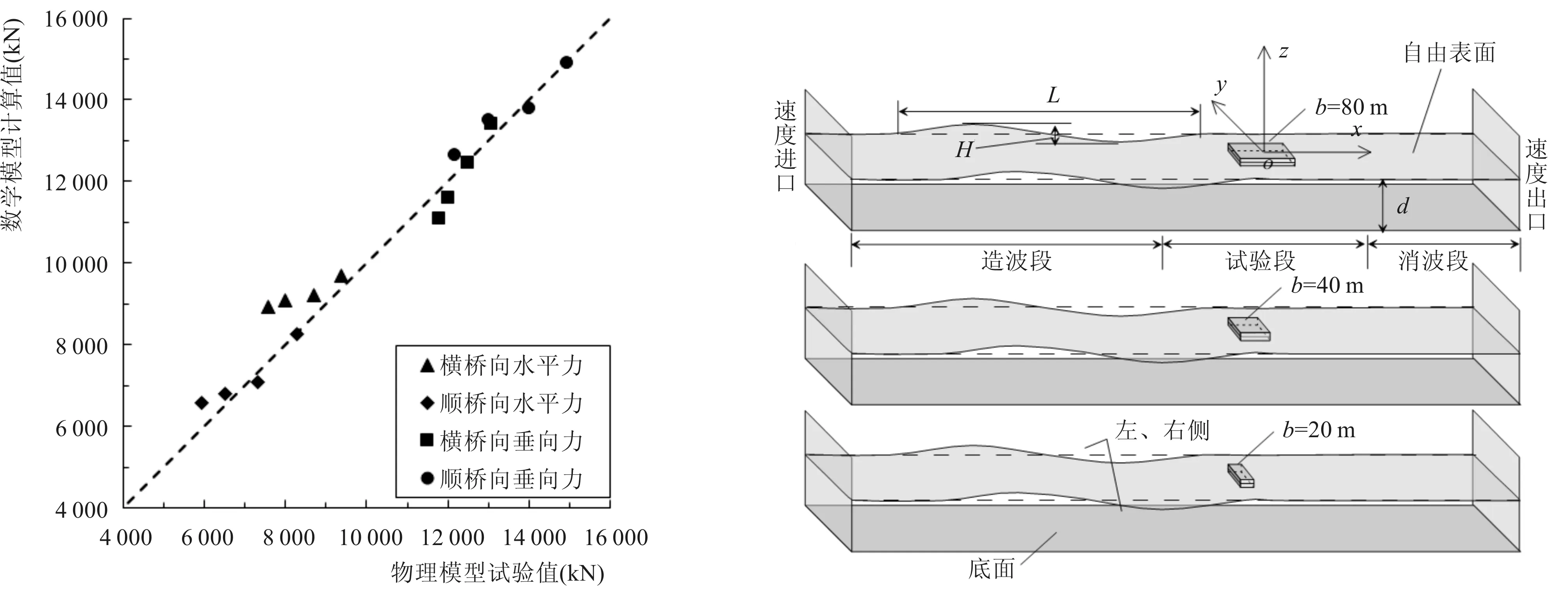
图3 承台水平力和垂向力计算值和试验值对比Fig.3Comparisonsbetweensimulatedvaluesandexperimentresultsofhorizontalandverticalforcesofcap图4 数值计算水槽示意图Fig.4Sketchofcalculationmodel

3 承台受力分析

3.1 计算参数

依据宁波舟山港主通道(鱼山石化疏港公路)跨海桥梁各通航孔主墩承台平面尺寸(含防撞装置)，其中：南通航孔主墩承台为49.66 m×34.00 m；主通航孔主墩承台70.20 m×47.20 m；北通航孔主墩承台40.00 m×22.60 m，并结合其他辅助墩和过渡墩承台尺寸。如图4所示，本文采用矩形承台结构尺寸来统一概化各种承台形状，暂不考虑承台形状对波浪力的影响，在试验过程中承台宽度a=40 m保持不变，承台长度b选取20 m、40 m和80 m三种长度，承台顶底高程统一取6 m和-2 m，海底高程统一为-21.5 m。

根据杨斌[14]2015年对舟山岛东北部沿海6个台风浪实测资料统计发现：深水区，谱峰周期在2.6～14.9 s之间，最大波高在0.77～5.19 m之间；浅水区，谱峰周期在2.5～17.2 s之间，最大波高在0.41～4.18 m之间。考虑当地波浪要素，入射波浪周期T选择8 s、10 s、12 s和14 s共4种，波高H选择2 m、3 m、4 m、5 m共4种。

考虑风暴潮增水等极端气候条件，研究淹没度对承台波浪力影响，本文设置多种计算水位。为了表示水位和承台顶底高程的相互位置关系，如图5所示，定义淹没系数Cs为淹没深度y与承台高度d1的比值(y为承台底部到水面距离) 。在承台位置固定的情况下，通过改变水位实现淹没系数的变化。

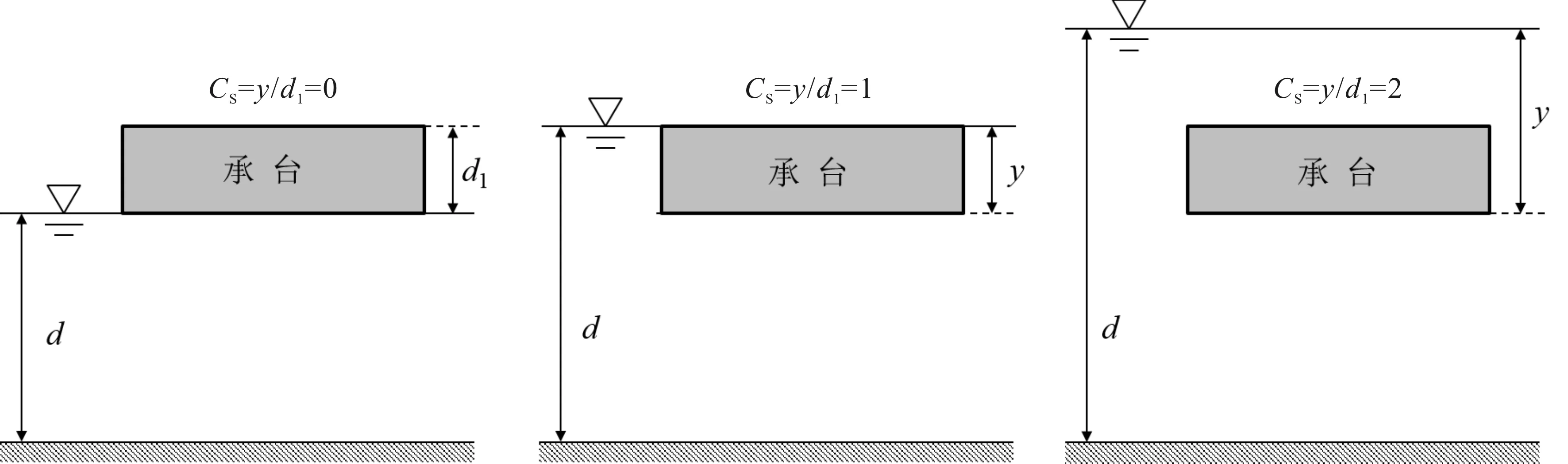
图5 淹没系数示意图Fig.5 Schematic diagram to investigate the effect of submersion depth

3.2 承台波浪水平力计算结果

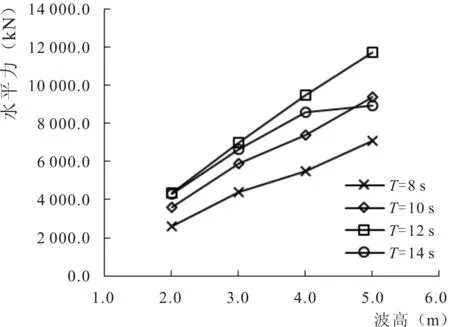
图6 承台水平力随波高变化关系Fig.6 Variations of wave horizontal forces with wave height

波高作为波浪的重要参数，直接影响波能大小，进而影响承台波浪荷载。图6是承台长度b=80 m时不同周期条件下承台水平力随波高变化情况，从图中可知，随着波高增大承台水平力也增大，且在本文计算条件下承台水平力随波高基本呈线性变化关系。当波高较大时承台波浪水平力和波高相关性较差，这是因为线性波作用时波浪的波高并不能无限增大，当波高增大时会导致波陡增大，波陡过大会导致波浪破碎，波浪破碎后会减弱波浪的能量，因此在拟合波高与波浪力关系时，波高越高非线性越强，拟合度越差。

图7为承台长度b=40 m时，承台水平力随淹没系数Cs变化规律，从图中可以看出承台水平力随淹没系数Cs增加呈3个变化区间：(1)当淹没系数Cs=0～1.0，水位从承台底面升至承台顶面，随着水位上升承台受力面积逐渐增加，承台水平力也逐渐增加；(2)当淹没系数Cs=1.0～1.4，水位刚淹没承台顶，然后继续上升，该区间波浪传播受承台影响大，随着承台顶水深不断加大，波浪在承台顶发生越浪→变形→传播，此时承台水平力随淹没系数Cs变化较小；(3)当淹没系数Cs=1.4～2.0，由于承台离水面距离逐渐增加，受波浪作用越来越小，承台水平力不断减小，从图中可以看出Ⅲ区承台水平力下降速率较Ⅰ区上升速率小。

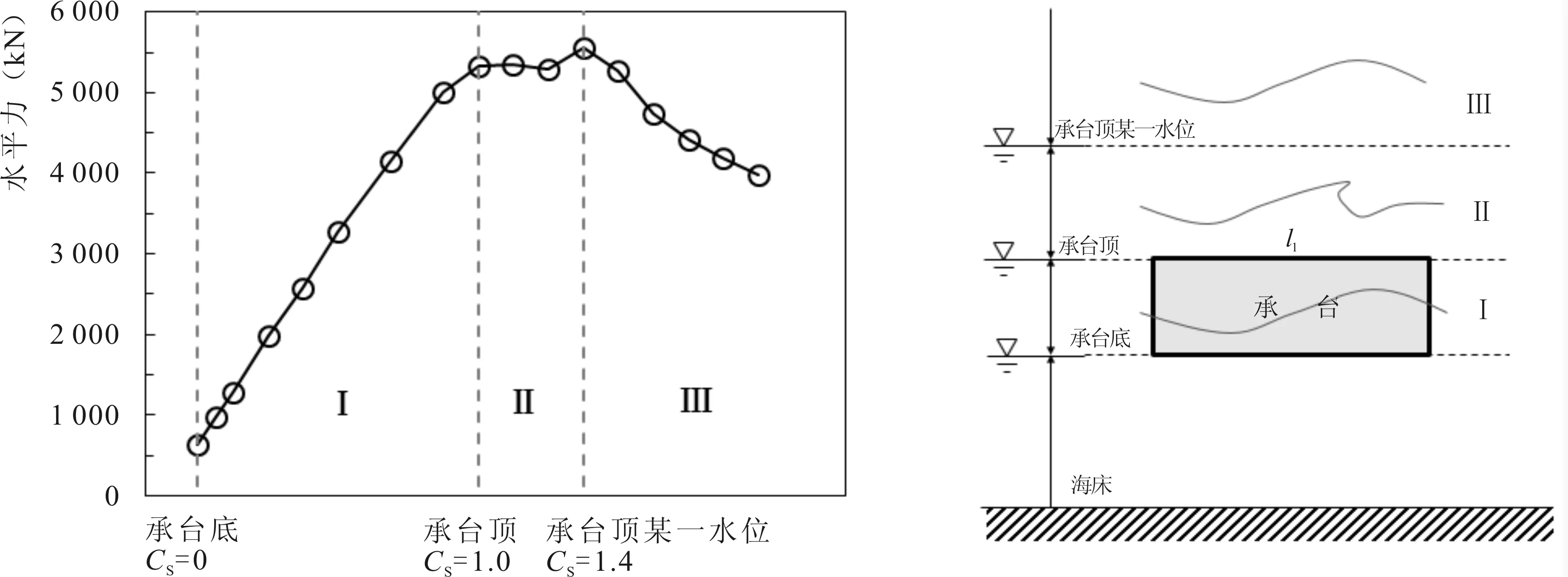
图7 承台水平力随水位变化规律Fig.7 Variations of wave horizontal forces with water level

图8是波高H=2 m和5 m时承台长度b=20 m、40 m和80 m条件下承台水平力随周期变化规律。从图中可知，不同波高条件下承台水平力随周期变化规律基本一致，承台水平力随周期变化规律主要受承台长度b影响：(1)承台长度b=80 m时，承台水平力先随周期增加而增大，当周期T=12 s后再随周期增加再减小；(2)承台长度b=40 m时，承台水平力先随周期增加而轻微增大，当周期T=10 s后再随周期增加轻微减小；(3)承台长度b=20 m时，承台水平力一直随周期增加而减小，初始减少速率较快，然后逐渐放缓。

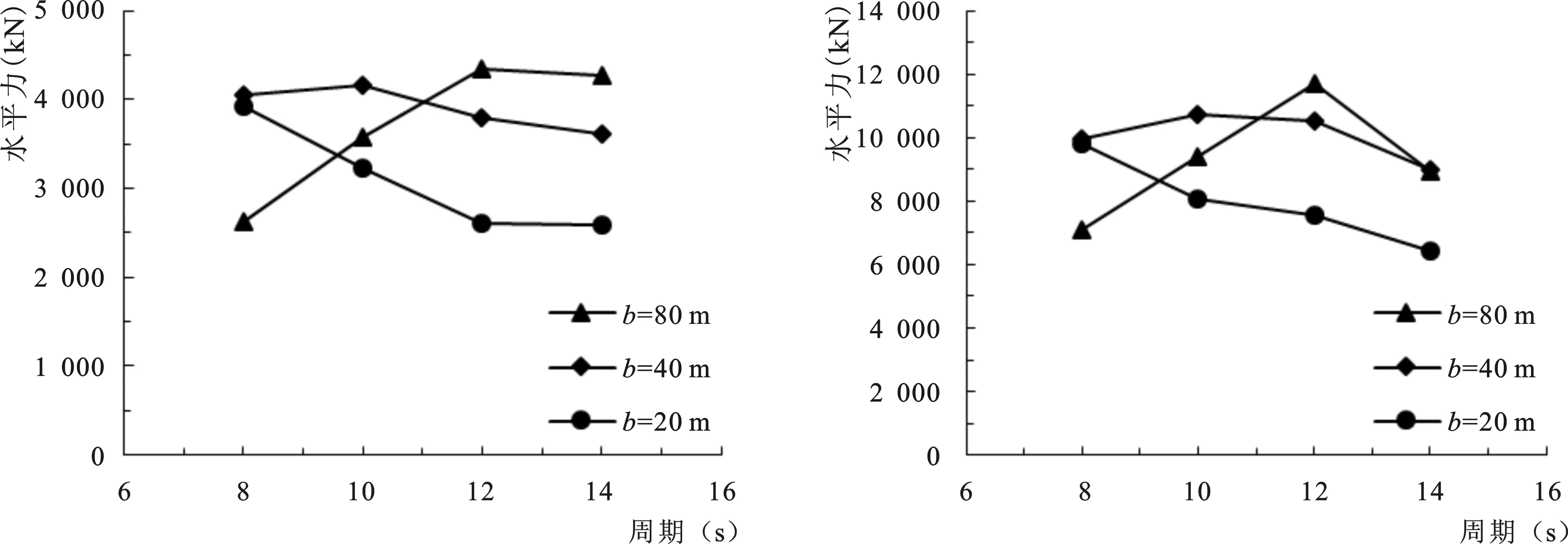
8-aH=2m8-bH=5m图8 承台水平力随周期变化规律Fig.8Variationsofwavehorizontalforceswithwaveperiod

定义无量纲化承台水平力fx为

式中：h、L分别为入射波浪波高和波长；a为承台宽度；b为承台长度；d为当地水深。

根据前人研究成果，承台水平力随周期变化规律主要通过波长和承台长度关系式kb表示。图9为淹没系数Cs分别为0.8、1.6和2.1条件下，承台水平力fx随kb的变化关系。从图中可知，不同淹没系数条件下，承台水平力fx随kb的变化规律基本相同，且可分为3段：在kb=0～1.0时，随着kb越大承台水平力fx越大，即波长相对承台长度越小承台水平力fx越大；承台水平力fx在kb=1.0～1.5时达到最大值；在kb=1.5～3.0时，随着kb越大承台水平力fx越小，即波长相对承台长度越小承台水平力fx越小。

3.3 承台波浪垂向力计算结果

承台处于静水状态中，只受到水体施加的浮力，随着波浪传播到承台位置，承台受水体施加垂向上的总力发生变化，波浪产生的垂向力等于垂直向上的总力减去初始承台所受浮力。图10是承台长度b=80 m时不同周期条件下承台垂向力随波高变化情况，从图中可知，随着波高增大，承台垂向力同样会增大，且在本文计算条件下承台垂向力随波高基本呈线性变化关系。和水平力随波高变化关系相似，波高越高非线性越强，承台波浪垂向力和波高拟合度越差。

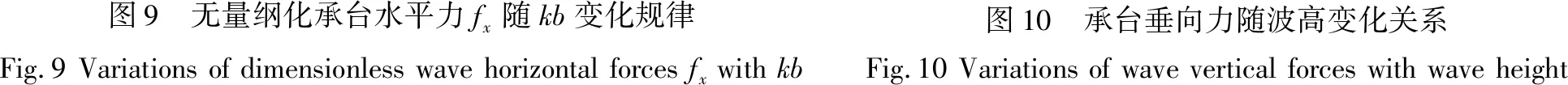
图9 无量纲化承台水平力fx随kb变化规律Fig.9Variationsofdimensionlesswavehorizontalforcesfxwithkb图10 承台垂向力随波高变化关系Fig.10Variationsofwaveverticalforceswithwaveheight

图11为承台垂向力随淹没系数Cs变化规律，从图中可以看出承台垂向力随淹没系数Cs增加也呈3个变化区间：(1)当淹没系数Cs=0～1.0，水位从承台底面升至承台顶面，承台底面离水面距离不断增大，承台底面所受垂向力逐渐减小；(2)当淹没系数Cs=1.0～1.7，水位从承台顶面继续上升，承台垂向力基本随着水位上升逐渐增加，分析认为，水位高于承台顶，承台受力面主要为承台顶面，初始阶段由于承台顶水深较小，波浪易破碎，当水深逐渐增大，波浪能够逐渐保持原有形态，从而承台垂向力逐渐增大；(3)当淹没系数Cs=1.7～2.0，由于承台离水面距离不断增大，受波浪作用越来越小，承台垂向力也逐渐减小。值得注意的是，图中Ⅰ区水位靠近承台顶、底面时，承台垂向力下降速率较中间段快，中间减小段接近线性变化。分析认为，当水位稍低于承台底时，波浪对承台底作用含有空气影响，导致垂向力较大；当水位稍高于承台顶时，波浪破碎，波能减小，垂向力减小较快。

定义无量纲化承台垂向力fz为

式中：Fbouy为1/2波高对应的承台浮力；fz为承台垂向力。

图12是淹没系数Cs分别为0.8、1.6和2.1条件下承台垂向力fz随波长-承台长度关系式kb变化关系，从图中可以看出，淹没系数Cs>1和Cs<1条件下承台垂向力fz随kb的变化规律不同。(1)当淹没系数Cs<1时，随着kb增加，承台垂向力fz逐渐减小，即相同承台条件下波长越长，垂向力fz越大；(2)当淹没系数Cs>1时，随着kb增加，承台垂向力fz先增后减，在淹没系数Cs=0.5～1.5之间承台垂向力存在最大值。根据图中承台垂向力fz随kb的变化关系，研究认为：

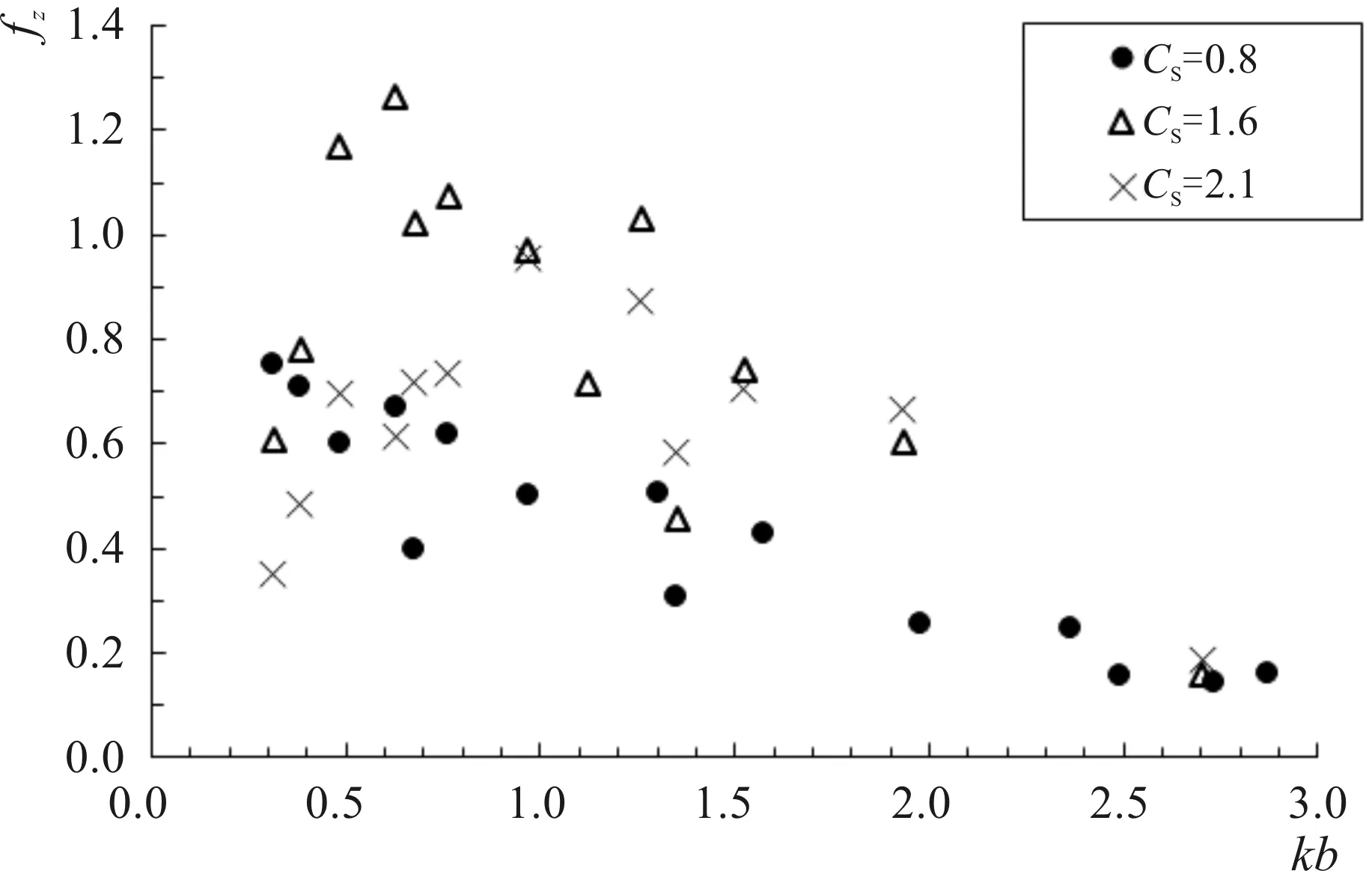
图12 无量纲化承台垂向力fz随kb变化规律Fig.12 Variations of dimensionless wave vertical forces fz with kb

(1)当淹没系数Cs<1时，承台垂向力fz和波长-承台长度关系式kb满足以下两个极端条件：

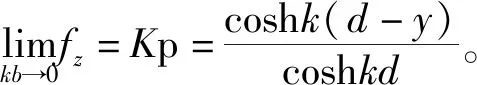
承台尺度越短，承台底部压强达到最大值的时刻越接近；同时，承台对承台底部遮蔽效应越小，承台垂向力也就越大。

(2)当淹没系数Cs>1时，承台垂向力fz和波长-承台长度关系式kb满足以下两个极端条件：

4 结论

本文通过Fluent软件建立了三维数值波浪水槽模型，进行了波浪和大尺寸承台相互作用的数值模拟研究，分析了波高、周期、淹没系数以及承台长度对承台水平力和垂向力的影响。研究发现：

(1)承台水平力及垂向力和波高呈线性变化关系，波高越大承台波浪力越大，但当波高越高时非线性越强，承台波浪垂向力和波高拟合度越差。

(2)随着淹没系数Cs增大，承台水平力先增加后减小，而承台垂向力先减小后增加再减小。

(3)承台相对水平力fx随kb先增后减，当kb=1.3左右时相对水平力达到最大。

(4)承台相对垂向力fz随kb变化关系受承台淹没系数Cs影响：当Cs<1时，承台相对垂向力fz随kb增加逐渐减小，其中当kb趋近于0时fz=Kp，当kb趋近于+∞时fz=0；当Cs>1时，承台相对垂向力fz随kb增加先增后减，其中当kb趋近于0和+∞时fx均趋近于0。