基于MPI+OpenMP的时间域航空电磁快速正演算法

任运通，李貅，齐彦福，曹华科

(长安大学 地质工程与测绘学院，陕西 西安 710054)

0 引言

时间域航空电磁法采用机载移动平台，通过线圈发射大功率一次场电磁波信号，利用接收线圈接收到感应的二次磁场，实现对地下电性结构及能源矿产分布的精细探测。该方法具有分辨率高、探测速度快、通行性极好等诸多优点,已被广泛应用于油气资源、环境工程和金属矿产等领域[1-6]。然而，传统的电阻率成像和一维反演技术已经无法满足三维问题解释的要求，开展三维反演解释技术研究是当前的热点问题，作为反演的基础，时间域航空电磁三维正演算法受到越来越多的关注。

目前，时间域航空电磁三维有限元正演方法主要分为间接法和直接法两种。其中的间接法是基于频率域麦克斯韦方程组，首先计算频率域响应，再通过时频转换方法转换到时间域[7-10]。由于间接算法存在稳定性差等诸多问题，人们普遍将研究方向转移到了时间域直接算法，直接求解时间域电磁响应。2010 年，Um等[11]采用非结构化网格剖分策略，对电性源的海洋三维瞬变电磁场进行了时间域矢量有限元的三维正演模拟计算。2016年，李贺等[12]人研究了直接时间域矢量有限元瞬变电磁三维正演模拟方法。2017年，齐彦福等人[13-14]基于航空电磁footprint的局部网格策略，利用非结构矢量有限元方法，对复杂介质情况下的时间域三维航空电磁响应进行了进一步模拟研究。然而，由于航空电磁法采用同时移动发射源和测点的方式进行观测，且采样密集，每次移动测点均需求解一次正演方程，产生巨大的计算量，传统的串行计算方法无法满足未来三维反演的效率要求。考虑到并行计算可以有效提高程序的运算效率，解决相同数量的问题所需执行的时间更短，开展了基于MPI+OpenMP并行技术的时间域航空电磁快速正演算法研究。

目前广为使用的并行加速技术有两种，分别是MPI(Message Passing Interface)和OpenMP(Open Multi-Processing)并行技术。MPI和OpenMP均需要与计算机语言结合使用，因两者较好的通信性和可移植性而受到广泛地应用。在尺度上，MPI多为基于多台处理机上的跨节点并行方法，OpenMP主要通过一些指令集对现有的Fortran或C/C++等程序进行扩展。并行技术在提高计算效率上具有显著优点，将该方法应用到地球物理数值模拟和数据处理中具有良好的前景。早在1997年，Newman和Alumbaugh[15]对三维大地电磁正演方法以及灵敏度矩阵进行了深入研究，成功将并行加速技术应用到了电磁反演当中，实现了多个节点的并行加速计算，极大推动了并行计算技术在地球物理领域的发展。国内对于并行计算技术应用到地球物理的研究，起步虽然稍晚于国外，发展却并不逊色。2005年荣莹等[16]实现了基于MPI的处理机集群并行计算系统平台的构建，在现有的硬件条件下提高计算力； 2006年，谭捍东[17]等结合MPI的优越性，通过频点并行的方式成功实现了大地电磁三维正演的并行计算，得到了很高的加速比，验证了并行算法的稳定性以及高效性；2011年，李小康[18]研究了频率域航空电磁法有限单元二维正演的并行计算；2015年，陈辉[19]研究了基于MPI的航空瞬变电磁一维正反演，提高了航空电磁一维模拟技术的计算效率。目前，对于并行加速技术在电磁方法数值模拟中的应用主要集中在大地电磁法，而航空电磁正演的并行算法研究依然停留在一维正反演和二维的频率域正演阶段。

本文将并行技术与时间域有限元算法相结合，基于三维航空电磁局部网格之间相互独立的特性[20]，通过采用MPI+OpenMP的并行加速策略，在保证正演结果可靠性的基础上，极大提高了时间域航空电磁有限元三维正演的计算效率。首先通过与串行有限元法和有限体积法进行对比检验本文并行程序的可靠性，然后进行计算效率分析，讨论并行加速比与硬件条件的关系，最后将该并行算法应用于复杂起伏地表模型，模拟其航空电磁响应。

1 方法理论

1.1 时间域航空电磁有限元正演理论

时间域麦克斯韦方程组可以表示为[21]

(1)

(2)

(3)

(4)

其中，t为时间，r为位置矢量，e(r,t)、j(r,t)、d(r,t)及b(r,t)分别表示r处在t时刻电场强度、电流密度、电位移矢量以及磁感应强度，q和μ分别表示累积电荷和磁导率。本文假定介质的磁导率与自由空间磁导率相同，即μ=μ0=4π×10-7H/m，介电常数与自由空间介电常数ε0相同，即ε=ε0=8.85×10-12F/m。电磁场之间具有如下本构关系：

j(r,t)=σe(r,t)+js(r,t) ，

(5)

d(r,t)=εe(r,t) ，

(6)

b(r,t)=μh(r,t) ，

(7)

其中：js(r,t)表示外部施加的源电流密度，h(r,t)和σ分别表示磁场强度和电导率。通过消去磁场，可以获得电场扩散方程

(8)

本文采用非结构矢量有限元方法进行空间离散，四面体单元中任意位置的电场可以表示为：

(9)

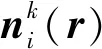
(10)

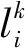
(11)

其中：M、S分别为质量和刚度矩阵，J为电流源项，针对每个单元，可由下面三式给出

(12)

(13)

(14)

其中V是单元的体积。由于各个单元相互独立，因此Mk、Sk和Jk可以采用OpenMP并行技术加速计算。针对发射源，将发射线圈分解为若干段导线，每段近似为一个电偶极子[24]每个电偶极子可以表示为：

js(r,t)=δ(r-rs)vI(t)dl。

(15)

上式中：I(t)表示t时刻的电流强度，dl表示电偶极子长度，v表示电流方向，δ表示脉冲函数。然后，利用二阶后推欧拉公式对有限元方程(11)进行时间域离散：

(3A+2ΔtB)ei+2(t)=A[4ei+1(t)-ei(t)]-2ΔtSi+2，

(16)

其中：Δt为时间步长，ei(t)表示第i时刻的电场值。式(16)亦可简写为：

Fe=P，

(17)

其中：F表示大型稀疏系数矩阵，P是右端项。当发射阶跃电流波形时，在0时刻之前发射线圈中供恒定电流，在全空间产生稳定的磁场，根据楞次定律可知空间中任意位置的电场均为0，故电场的初始条件为：

e(r,0)=0 。

(18)

采用狄利克雷边界条件，根据电磁波在空间中的几何指数衰减规律，可以通过加大计算区域的扩边范围，使其满足

e|Γ=0 ，

(19)

其中Γ表示计算区域的外边界。最后，采用直接求解器Pardiso对线性方程组进行求解，即可获得全空间的电场值，再利用法拉第电磁感应定律(式(1))计算磁场响应。

1.2 局部网格正演计算技术

大量的数值实验表明三维数值模拟结果的精度受到网格质量的影响非常大，因此需要对导电大地和发射源进行精细的网格剖分来获得高精度正演结果。传统的时间域航空电磁三维正演模拟算法采用全局网格加密方式，即通过一套网格对所有测点的电磁响应进行模拟。然而，由于航空电磁法采样密集且观测剖面长，导致正演网格单元数量巨大。如果采用全局网格进行正演模拟，将产生巨大的计算量，严重降低计算效率。考虑到航空电磁系统影响范围有限(如图1所示)，本文采用局部网格加密技术，针对每个测点或者相邻的几个观测点分别设计独立的网格，并分别在局部网格上进行正演模拟，以此在保证结果可靠性的同时提高计算效率。

图1 航空系统影响范围示意Fig.1 Moving footprint for time-domian airborne EM system

局部网格技术根据航空电磁系统的影响范围设计合理的局部精细网格。图2展示了全局网格和局部网格，其中图2a表示全局网格，图2b、c、d则分别表示针对测线上不同测点所设计的相互独立的局部网格。从图中可知全局网格对测线上所有测点、测线下方地空分界面以及异常体部分均进行了相对细致的网格剖分，因此造成网格数量较大，导致正演模拟的计算量剧增，计算效率降低。而局部网格仅仅对异常体、当前测点位置以及其下方的地空分界面进行局部加密，对单个测点进行单独求解，因此所使用的网格数量大大降低，计算量减小。

2 并行加速

2.1 基于OpenMP的并行加速

OpenMP采用分叉—合并(Fork-Join)执行模式。一个OpenMP程序开始于一个单一的线程，该进程又称作主线程，通过并行指令对程序的并行区间进行定义，在这个区间中程序块由多个线程自动分配任务及并行执行，线程数由主线程决定，在一个大型程序中可以嵌套多个OpenMP并行区间，其中并行区间由一组$OMP指令进行开启(!OMP PARALLEL)和关闭(!OMP END PARALLEL)。图3是OpenMP并行模式的示意图。

2.2 基于MPI的并行加速

MPI需要用头文件use mpi进行声明，然后在主进程(即节点)中进行初始化，开启MPI并行环境，获取进程个数及编号，再将多个任务合理地分配到各个进程并传输对应的数据，然后分别进行计算，最后汇集到主进程并关闭并行环境，如图4所示。

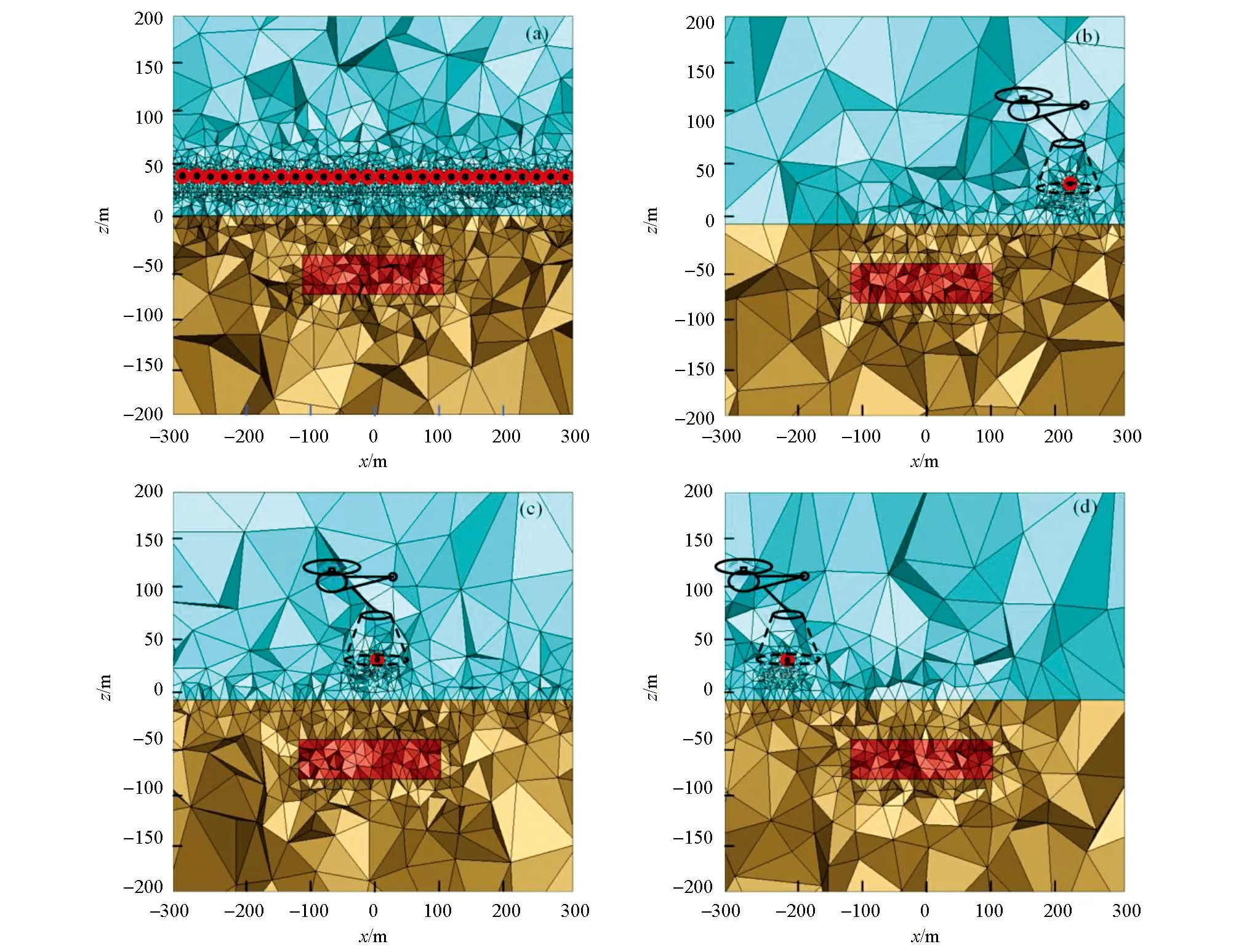
图2 全局网格与局部网格对比 (a为全局网格；b、c、d为局部网格)Fig.2 Global grid vs. local grid ((a) is a Global grid; (b) (c) (d) is a local grid)

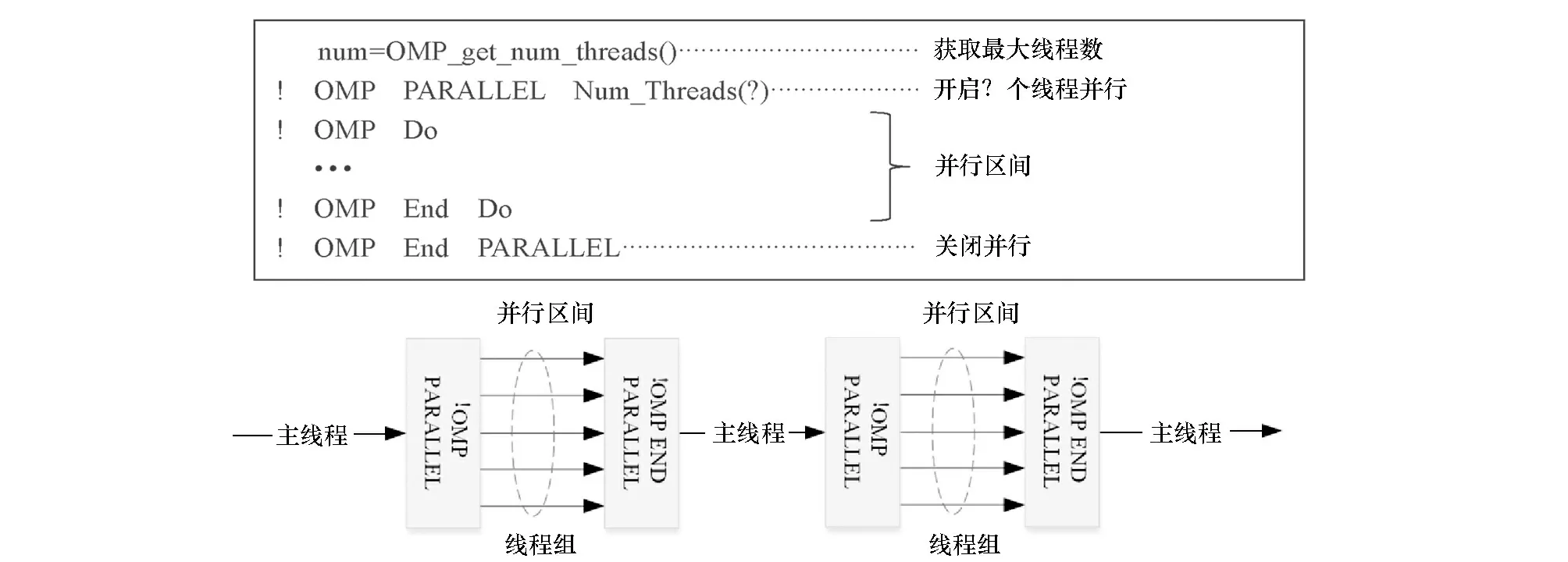
图3 OpenMP并行模式示意Fig.3 OpenMP parallel mode schematic

2.3 并行程序设计及实现

由于航空电磁系统在每个观测点处的灵敏区域相对于总计算区域来说远远不及，因此仅仅在观测点的一定位置范围内对网格进行加密即可满足计算的精度要求，针对每个观测点分别单独设计独立的网格来提高计算效率。

时间域航空电磁三维正演各个测点计算相互独立，不存在数据依赖关系，具有非常好的并行性，在三维正演的基础上实现了基于MPI的多测点并行计算，在独立网格内实现了基于OpenMP的单元矩阵并行计算。程序采用主从模式，整个程序的基本结构及运行流程由主进程把控，主要负责读取模型参数、数据传输以及对并行任务的分配，子进程负责接收来自主进程传递的消息、对分配的任务进行计算以及输出本进程的计算结果。为了充分利用计算资源提高计算效率，主进程在完成任务分配和数据传输的工作后也参与到测点的并行计算当中。

具体实现的流程如图5所示，主进程读取模型的整套网格参数，随后将其传递给其他子进程，之后各进程根据分配的网格参数计算模型的响应结果，为了防止数据传输时发生通信冲突，采用各进程分别输出各自的计算结果。

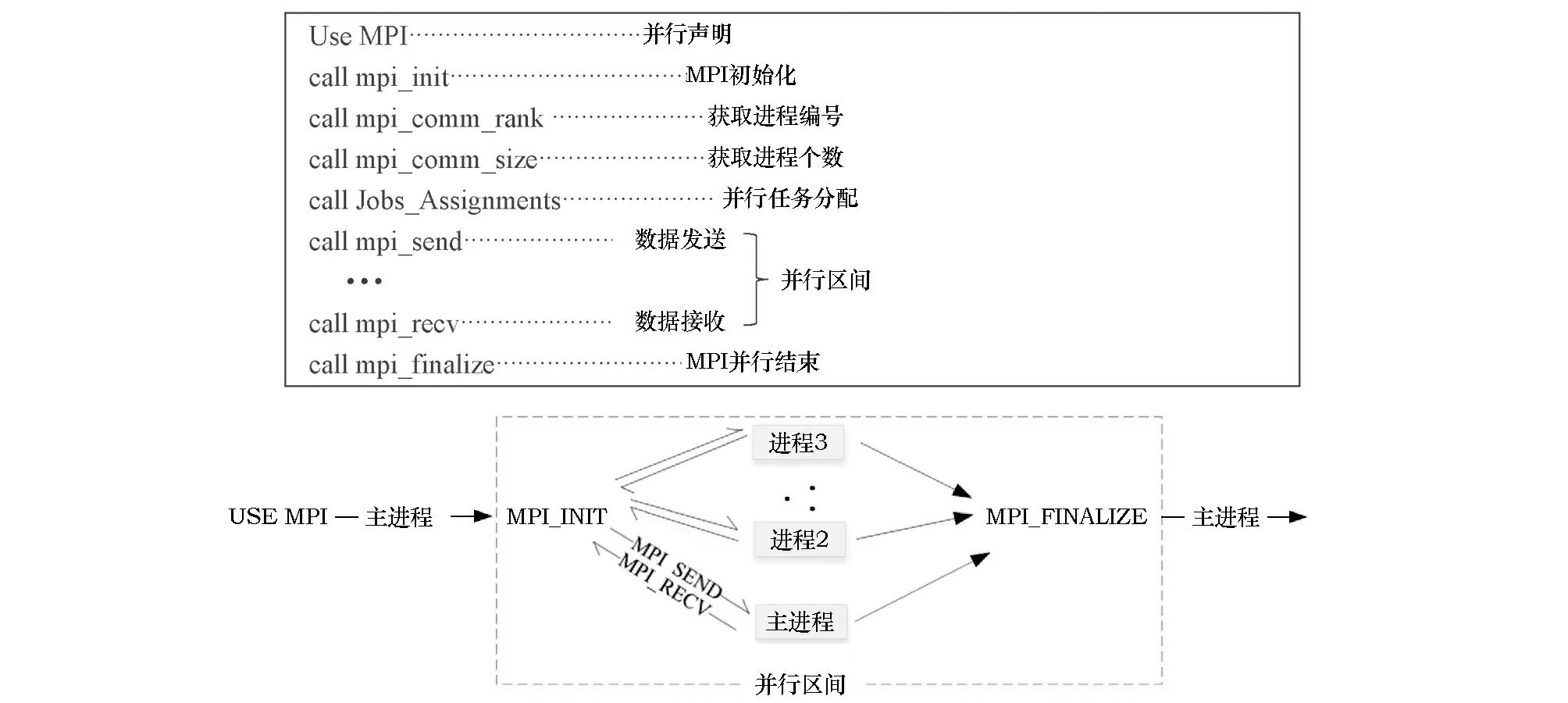
图4 MPI并行模式示意Fig.4 MPI parallel mode schematic

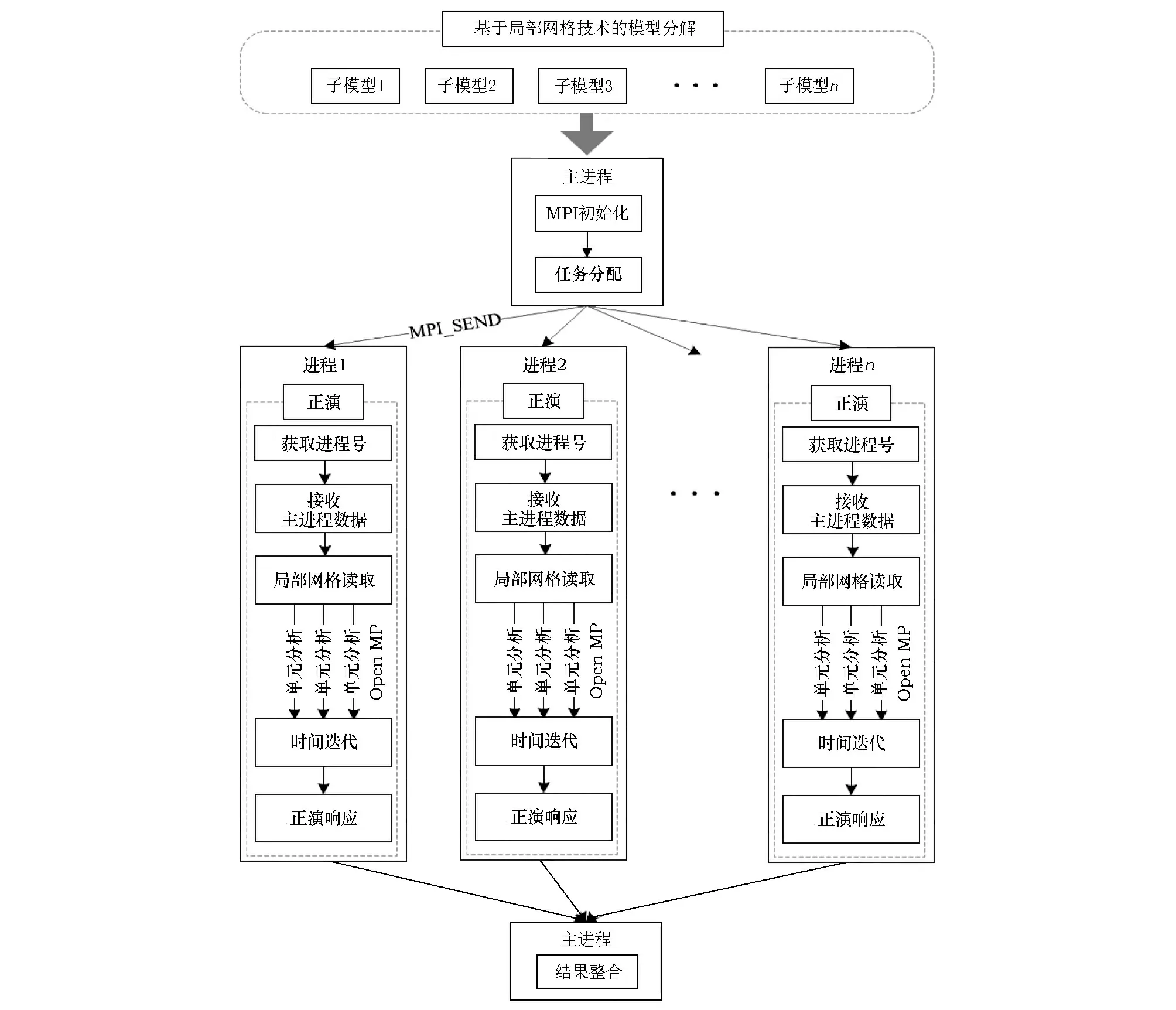
图5 航空瞬变电磁三维正演并行计算流程Fig.5 Airborne transient electromagnetic three-dimensional Forward modeling parallel computing flow chart

3 模型算例

3.1 精度验证

为检验本文所开发的时间域航空电磁多粒度并行正演方法的正确性，设计了如图6所示的水平板状体模型，发射波形为阶跃波，发射电流强度为435 A，通过全局网格和局部网格两种剖分方式，对异常体上方y=0 m剖面上-400～400 m范围内的32个测点，分别进行正演模拟，且将正演结果与有限体积方法的正演结果进行比对，进行数值精度验证。

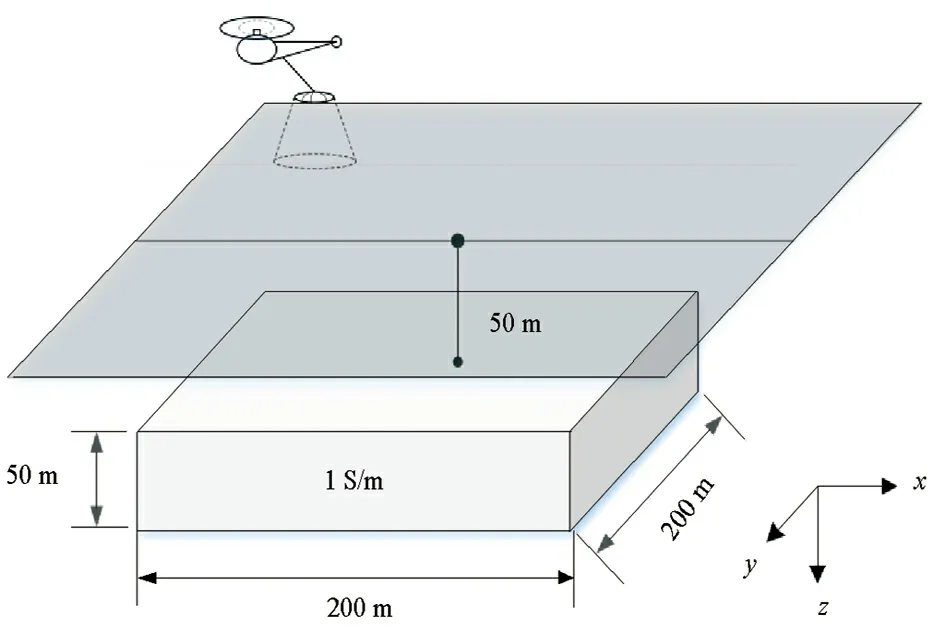
图6 水平板状体模型示意Fig.6 Schematic diagram of the horizontal plate model

使用的集群服务器有16个型号为Intel(R) Xeon(R) CPU E5-2609 v4 @ 1.70 GHz的逻辑CPU，每个CPU拥有2G内存和4个线程。采用时间域有限元全局网格法、基于多粒度并行加速策略的时间域有限元局部网格法以及有限体积方法分别计算的电磁响应结果如图7所示，可以清楚地看出，上述3种不同方法所计算的结果吻合得非常好，且均对模型中的地下板状体有明显反映。这一结果有效验证了本文并行算法的精度。

3.2 并行性能分析

为了分析基于MPI+OpenMP并行加速策略的时间域航空电磁三维正演程序的并行加速效果，采用上述水平块状体模型进行测算，根据控制变量法，控制计算测点数为32和线程数为4保持不变，依次对不同数量的进程进行比较，通过加速比和并行效率两个参数来评估本文设计的三维正演并行程序。

令原有的串行程序在集群服务器单进程上的运行时间为Ts，经过多粒度并行优化后，运行所需时间为Tp，其中P表示开启的进程数，则加速比Sp可表示为：

Sp=Ts/Tp，

(20)

并行效率可定义为：

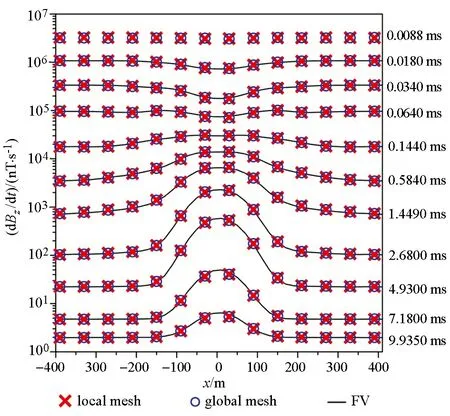
图7 全局网格串行计算和局部网格并行计算电磁响应结果对比Fig.7 Comparison of electromagnetic response results between global grid serial computing and local grid parallel computing

ep=Sp/P。

(21)

测试结果见表1。在计算测点数一定时，随着进程数的增加，计算时间呈非线性下降趋势，加速比逐渐增大，相反并行效率逐渐降低；当开启16个进程时，采用多粒度并行加速后执行耗费的时间仅仅是串行程序耗时的1/10，同时并行效率达到最低。

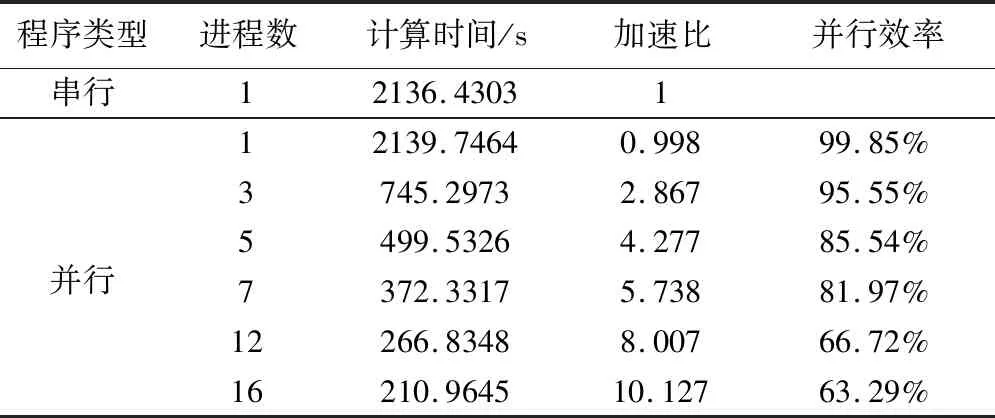
表1 基于MPI+OpenMP并行加速策略的行正演计算统计Table 1 Line forward calculation statistics based on MPI+OpenMP parallel acceleration strategy

由图8可以发现以下特点：并行化后的正演程序加速比与开启的进程数并不是整数倍关系，而是呈非线性增长，且并行效率整体呈降低趋势。这是因为在集群服务器上开启并行环境后，会占用一定内存，且进程间进行数据传递需要占用时间，而且任务量与开启的进程数不匹配时，计算任务少的进程会率先完成计算量，但该进程并不会结束，而是要等待未完成任务的进程，从而导致时间的损耗。所以开启P个进程，加速比Sp并不能达到P，且随着进程数的增加Sp与P的差值越来越大。

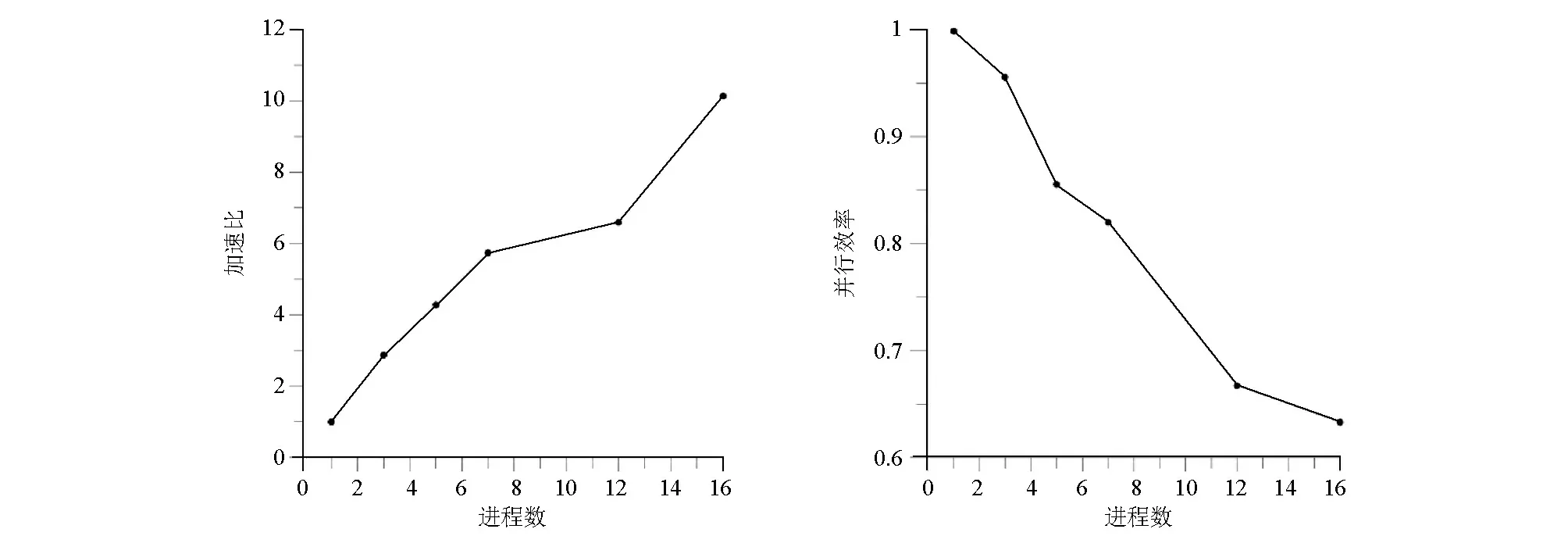
图8 不同进程数的加速比(a)和并行效率(b)Fig.8 Acceleration ratio (a) and parallel efficiency (b) for different node numbers

3.3 复杂模型计算

考虑到地形起伏不平对航空电磁正演结果的影响较为严重，采取四面体网格进行加密剖分后的计算量较大，从而导致计算时间较长，因此利用多粒度并行加速技术进行加速计算。导入地形文件数据模拟起伏地表，并设计地下埋藏有块状及倾斜板状良导体(图9)。设高阻围岩的电导率为0.01 S/m，块状体和板状体的电导率为1 S/m；倾斜版状体顶部埋深60 m，垂直深度250 m，块状体顶部埋深50 m，边长200 m。采用中心回线装置，飞行高度30 m，发射线框半径15 m，线圈匝数为1，采用阶跃波激发。全区设置11条测线，每条测线布设171个测点，共计1 881个测点，每个网格单元数约90 000个，正演过程共需进行9 350次矩阵分解，327 250次回代。若采用传统串行计算时，总耗时约1 968.623 min(32.8 h)，采用并行加速开启16个进程后总计算时间约194.336 min(3.24 h)，消耗内存约5.2 G，效率提高了10.13倍,如表2所示。

表2 计算情况统计Table 2 Calculation statistics table

图10是主剖面(x=0测线)的多测道图，可以看出在早期表现出地形的响应，到了晚期，地形影响逐渐变小，表现出异常体的响应。图11呈现出整个测区在四个时间点时的航空电磁响应结果，从图中可以明显看出在时间早期，仅存在地形的响应，由于地形凸起，电磁响应呈现出相对低异常，在x=0，y=-500附近，相对低异常达到极大值，由于块状异常体处于凸起地形下方，相对于倾斜板埋藏较深，故随着时间延长，倾斜板的异常响应率先显示出来，随后出现块状体异常响应，且由于地下埋藏有异常体，导致地形的影响减弱，到晚期时，电磁波穿过异常体，仅剩地形的电磁响应。

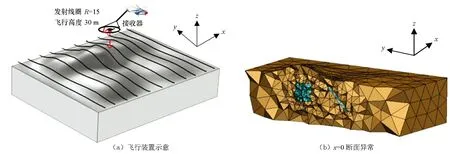
图9 复杂模型计算Fig.9 Calculation of complex models

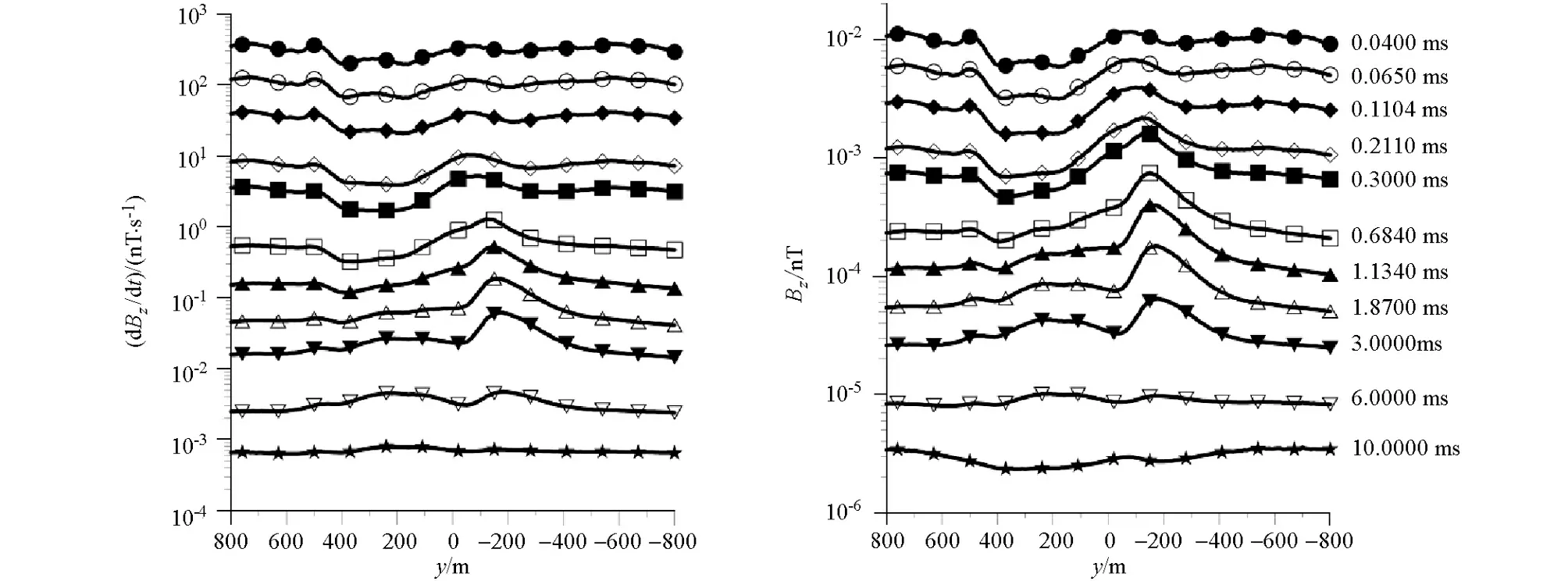
图10 复杂模型主剖面(x=0测线)多测道曲线Fig.10 Multiple trajectory map of complex model main section (x=0 line)

4 结论

利用MPI实现了三维正演模拟中的多测点并行计算和实现了独立网格内单元矩阵计算的OpenMP并行加速，最终实现了基于MPI+OpenMP并行加速策略对时间域航空电磁三维正演方法的并行化，并得出并行化后的正演程序，其加速比随着开启的进程 数增加呈非线性增长。

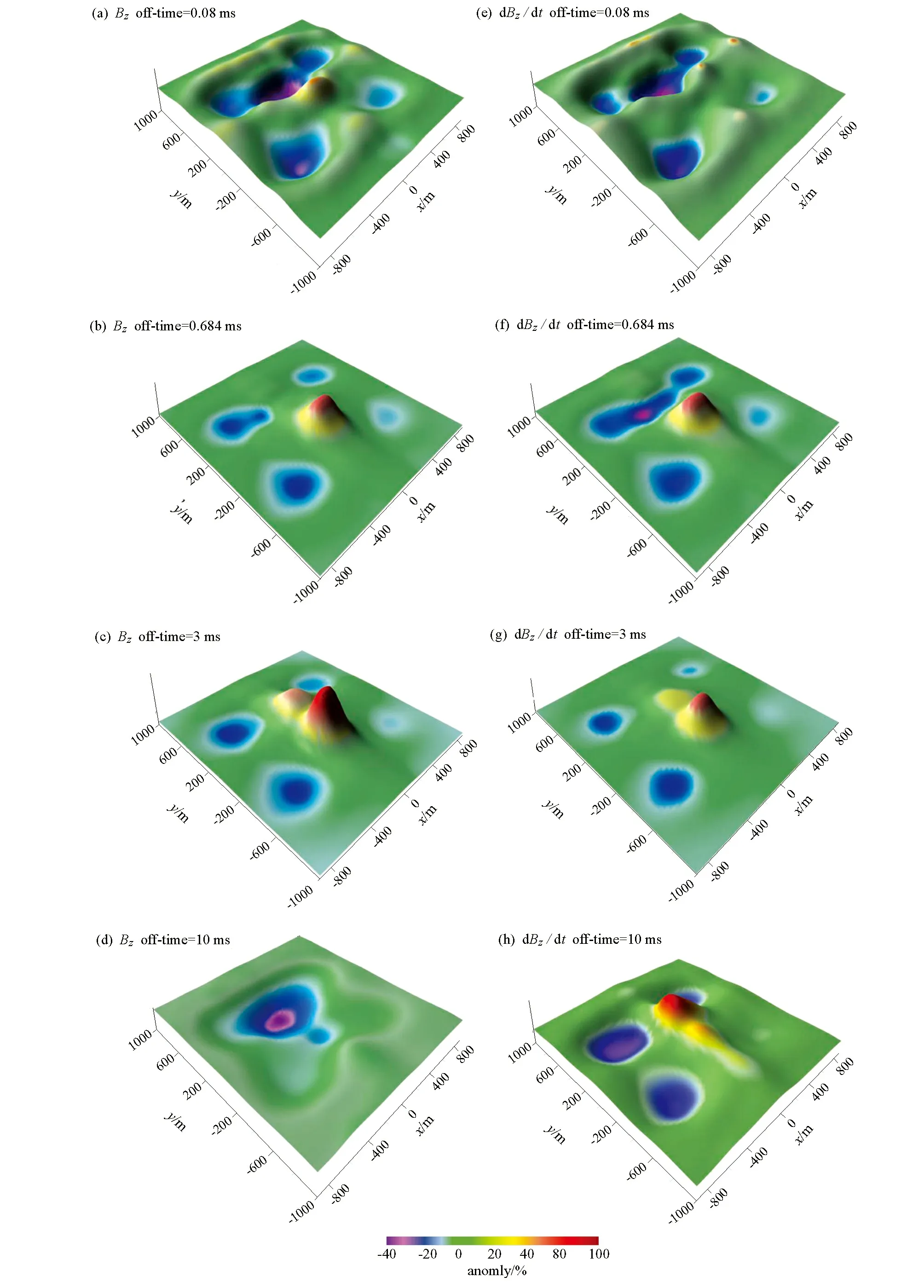
图11 复杂地形响应曲面Fig.11 Complex terrain anomaly response surface map

由于“并行开销”的存在，开启的进程数越多，并行效率整体呈现出下降趋势，即使只开启一个进程，效率也比串行效率低。地形起伏模型的数值模拟体现了本文并行优化后的正演方法的高效性，正确高效的三维正演为三维反演提供了可能。