强吸收弱散射介质下的鬼成像实验研究

马云强，张子进，吴承启

（上海理工大学 理学院，上海 200093）

引 言

随着科学技术的不断提高，人们对成像质量的要求也越来越高，特别是在一些复杂的医学环境中。传统成像因其衍射极限的限制，复杂环境下的成像效果非常差，很多方法可以突破衍射极限成像[1]，其中鬼成像引起了广泛的关注[2-6]。与传统成像不同的是，鬼成像（GI）中一般有两条光束：一束通过包含物体的物臂，仅由单像素桶探测器探测到，另一束通过不包含物体的参考臂，记录有关光源的信息。本文采用最基本的鬼成像架构，设定实验所需参数并将物体置于强吸收弱散射介质中，最终将单像素探测器收集到的光强信息和CCD收集到的光源信息进行关联计算，从而得到物体的像。通过对鬼成像和传统成像直接进行对比可以发现，鬼成像在一定程度上削弱了散射的影响。当介质散射性质不变而吸收性逐渐增强时，传统成像的对比度逐渐降低而鬼成像基本保持不变。对成像结果的峰值信噪比进行分析可知，鬼成像在强吸收弱散射介质中成像优于传统成像。

1 实验架构设计及原理

激光照在旋转的毛玻璃上产生所需的赝热光源S，实验原理图如图1所示，用分光棱将赝热光分成两束：一束通过包含物体的物臂上，此束光通过含有物体的介质，又被另一个分光棱镜（BS）分成两束，一束通过透镜f1由单像素桶探测器Dt收集，另一束通过透镜f2由CCD1收集；另一束通过不包含物体的参考臂，经过透镜f3由CCD2收集。其中，Z1表示毛玻璃到容器左表面的距离，L1和L2表示双缝物体距离容器左表面和右表面的距离，Z2表示容器右表面到透镜f1的距离，Z3表示透镜f1到单像素桶探测器Dt的距离；Z4表示容器右表面到透镜f2的距离，Z5表示透镜f2到CCD1的距离；Z6表示毛玻璃到物体共轭面的距离，Z7表示物体共轭面到透镜f3的距离，Z8表示透镜f3到CCD2的距离。参看图片内容单像素桶探测器Dt收集到的带有物体的光强总值信息与CCD2收集到的光源信息进行关联运算（correlation），最后得到鬼成像中的物体信息。CCD1收集到的物体信息直接叠加即为传统成像的物体信息。

在透镜f1和f2的前面放置一个光阑，通过调整光阑的内径使关联成像与鬼成像的分辨率保持一致，同时需要满足以下关系[7-8]

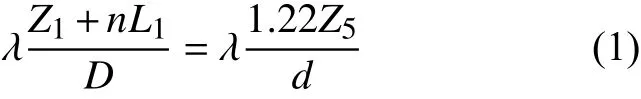
式中：λ为激光的波长；n表示介质的折射率；D为激光照在毛玻璃上的光斑直径；d为光阑的内径。物平面和测试探测器平面服从高斯薄透镜方程

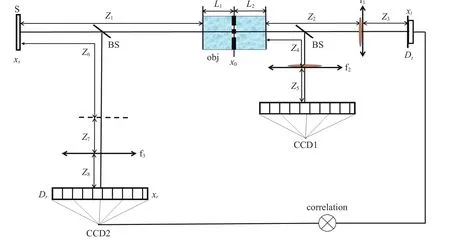
图1 实验原理图Fig. 1 Experimental schematic

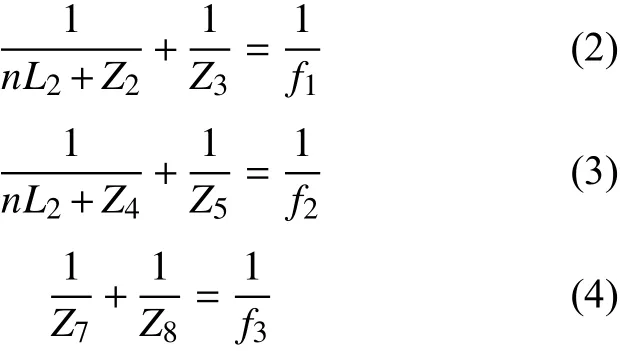
式中：f1、f2、f3分别为透镜f1、f2、f3的焦距。

图1中，对于参考臂，在菲涅耳近似的前提下，点扩散函数可以表示为

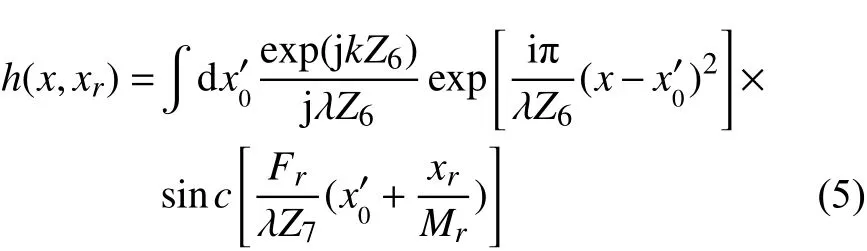
式中：Lr表示透镜f3的直径；Mr=Z8/Z7为参考臂的放大率； s inc(ξ)=sin(πξ)/(πξ) 为与参考臂透镜相关的一维点扩散函数，同时我们考虑了透镜的有限孔径。

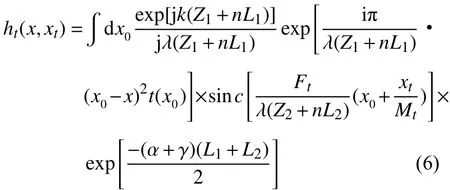
式中：Lt=d表示光阑的内径；Mr=Z3/(nL2+Z2)为物臂的放大率； s inc(ξ)=sin(πξ)/(πξ) 物臂对应的一维点扩散函数；α和γ分别表示吸收系数和散射系数。根据鬼成像理论，物体的信息可以表示为

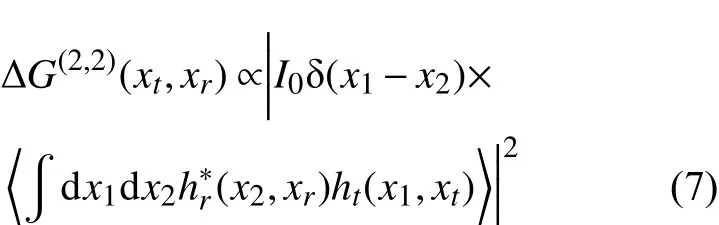
式中：＜·＞表示求平均；δ为狄拉克函数。

由于介质的散射和吸收性质，物臂上的点扩散函数很难写出具体表达式，我们运用统计光学理论来进行鬼成像计算，可以通过使用以下统计学的公式来获取介质溶液中物体的信息G[10]

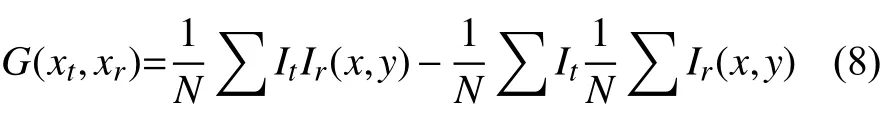
式中：It表示物臂收集到的光强值；表示参考臂在点处收集到的光强值；N表示样本数量。

2 实验结果和分析

实验中的介质是将0.2 g的CaCO3粉末加入到80 mL甘油中混合均匀制成。CaCO3粉末的颗粒直径 a≈10 μm，即 2 πa/λ =118.1 ，满足米氏散射。如图2所示，在介质中加入不同体积的牛奶来改变介质的吸收强度，其中，图2（a）~（f）分别表示加入0.1 mL、0.2 mL、0.3 mL、0.4 mL和0.5 mL的牛奶溶液，由于加入的牛奶体积相较于整个溶液很少，可近似认为体积没有发生变化，用β表示牛奶在整个介质溶液中占的百分比。

图2 不同体积牛奶的散射介质图Fig. 2 Photograph of the scattering medium with different volume of milk

实验中所使用的物体是一个双缝，缝宽a=0.1 mm，双缝中心间距b=0.3 mm，缝高h=1.0 mm，其中Z1+nL1=150 mm, Z5=150 mm, D=5 mm, d=2.5 mm必须满足式（1）。其它参数设置f1=75 mm, Z2+nL2=150 mm, Z3=150 mm, f2=75 mm, Z6=366 mm, Z7=Z8=100 mm, f3=50 mm和L1=L2=25 mm。桶探测器和CCD摄像机的曝光时间窗口设置为30 ms，采样频率为2 Hz。这样可以确保在采集更多的样本的同时没有失帧。CCD 的像素尺寸为 3.45 μm×3.45 μm，CCD 相机记录的散斑图案尺寸为600像素×400像素。传统成像和鬼成像的样本数都是9 000张。

传统成像中，介质置于物体所在光路前面，对成像是没有任何影响的，这是传统成像机制决定的，只有介质置于物体所在光路后面，成像才会受到影响。鬼成像中，实验已经证明，介质置于物体后对成像结果没有影响，那么，置于前面是否有影响，我们可以通过下面实验来探究并比较。实验中，要得到传统成像的图像，需要将物体放置在介质的左侧，即L1=0 mm, L2=50 mm。相应的参数也应该调整为Z1=366 mm, Z4+nL2=Z5=150 mm，f2=75 mm。同时，要得到鬼成像的图像，需要将物体放置在介质的右侧，即L1=50 mm, L2=0 mm。相应的参数也应该调整为Z1+nL1=366 mm, Z2=Z3=150 mm， f1=75 mm，Z6=366 mm，Z7=Z8=100 mm和f3=50 mm。

实验结果表明，在传统成像中，CaCO3粉末表现出了介质的散射特性如图3（a）所示，双缝的周围有明显的散射光。随着牛奶浓度的增加，介质的吸收性变大，双缝的成像效果越来越差，可见度越来越低。在鬼成像中，散射几乎对成像没有影响，如图3（b）所示。此外，随着介质吸收性的增加，成像的性能没有显示出下降。因此，我们可以很容易地得出结论，鬼成像可以大大降低吸收对成像的影响。

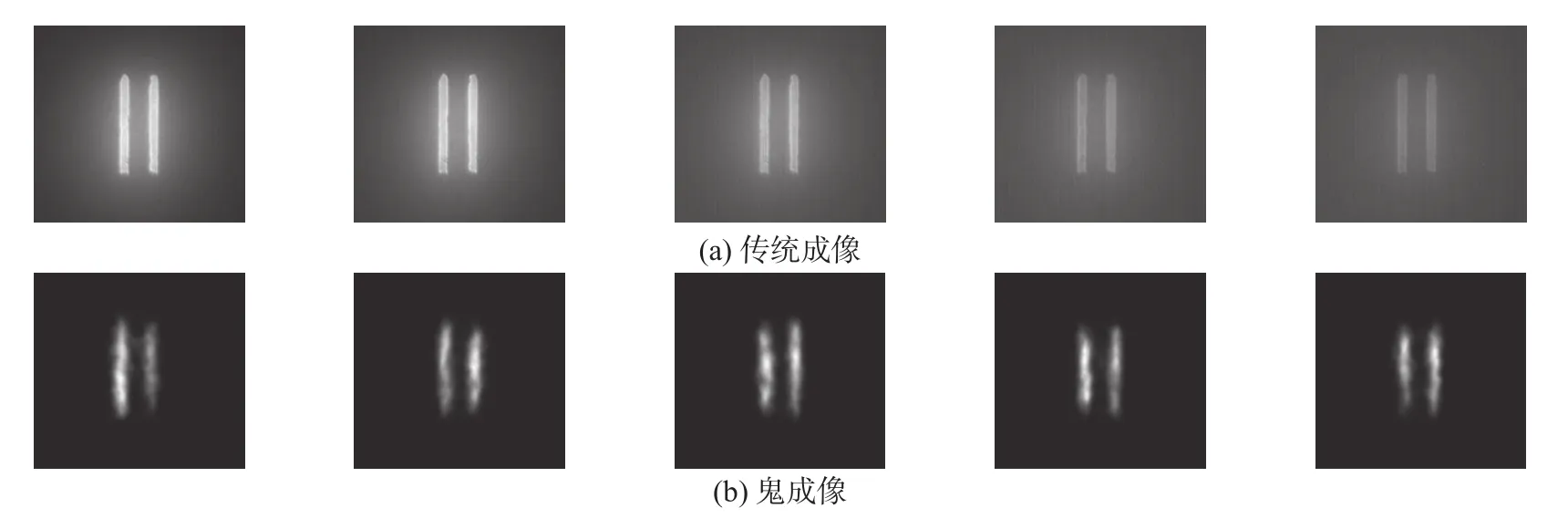
图3 随着吸收强度的增加，成像的比较Fig. 3 Images of the object obtained as the strength of absorption is increasing

为了准确地进行比较，我们引入峰值信噪比（PSNR）用于定量描述图像质量[11]

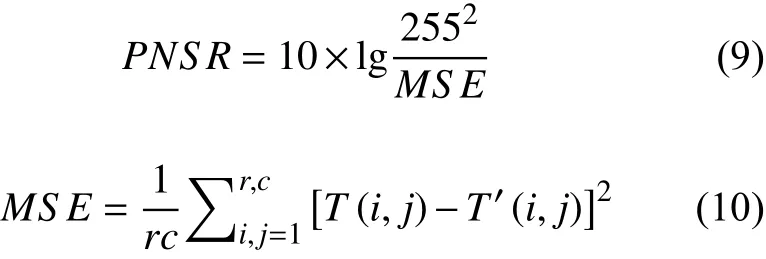
式中：T表示原物的信息；T'表示成像信息；r和c表示像素的行和列。通过相应的峰值信噪比对比，如图4所示。我们可以很清楚的得出，鬼成像的PNSR值要远高于传统成像，尤其是在强吸收的条件下。例如，当牛奶的比例是0.125%时，ΔPNSR=2；当牛奶的比例是0.625%时，ΔPNSR=4。

3 结 论

本文以鬼成像的基本理论为依据，通过对传统成像与鬼成像的实验结论对比与分析，可以得出，散射对鬼成像没有影响，随着介质的吸收性增加，传统成像中的PSNR值减小；在鬼成像系统中，PSNR值基本保持不变，这意味着鬼成像可以在很大程度上削弱环境的影响。该实验的结果将为浊度和生物系统成像的研究提供参考。

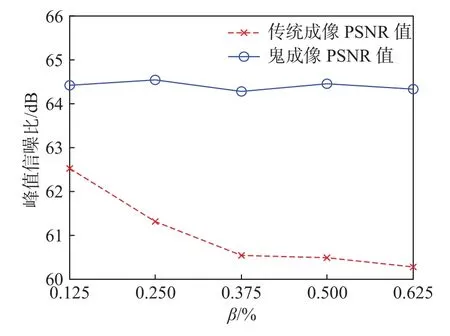
图4 PSNR值随散射介质中的吸收强度而变化。Fig. 4 The value of the PSNR varies with the concentration of absorption in scattering medium.