基于SPH-FEM耦合法切缝药包爆破机理数值模拟

程 兵，汪海波，宗 琦

（安徽理工大学土木建筑学院，安徽 淮南 232001）

1 引言

自1978年W.L.Fourney等［1］提出在炮孔中采用切缝药包实现定向断裂控制爆破以来，切缝药包在提高爆破成型质量、减少围岩损伤等方面一直发挥着重要作用。近年来，针对切缝药包定向断裂的破岩机理及其进一步推广应用，国内外学者开展了大量研究工作并取得显著成果。杨国梁等［2］将切缝药包应用于掏槽爆破，数值模拟和现场试验结果都表明：采用切缝药包进行掏槽爆破能够显著提高巷道开挖效率。杨仁树等［3-4］应用电镜扫描技术获取了切缝药包爆破裂纹断面形态特征，从微观角度探究了定向破岩机理，并使用切缝药包进行硬岩巷道光面爆破，现场试验结果表明：切缝药包能够提高炮孔利用率和降低围岩损伤。谢华刚等［5］提出了一种新型切缝药包，并通过数值模拟和理论分析阐明该新型切缝药包定向爆破效果优于传统切缝药包。魏晨慧等［6］采用数值模拟探究了围压对切缝药包爆破裂纹演化的影响规律，结果表明裂纹扩展受制于围岩压力。Wang［7］、张士春等［8］通过试验和数值模拟，研究了采用不同介质进行径向不耦合装药时切缝药包爆破效果。李清等［9］基于有机玻璃板进行切缝药包爆破试验，研究了不同药量切缝药包双孔爆破裂纹扩展规律。张胜利等［10］比较了切槽炮孔和切缝药包的爆破效果，认为切缝药包在定向断裂方面具有独特优势，并对比不同工况爆破效果得到最佳切缝宽度。岳中文等［11-13］利用数字激光动焦散线光测试验技术，研究了起爆时差对切缝药包双炮孔间裂纹扩展和贯通的影响，并结合数值模拟探究了切缝管内不耦合装药与耦合装药时切缝药包爆破效果，以及不同炮孔间距下切缝药包爆破裂隙扩展与贯通规律。

数值模拟在爆炸冲击问题的研究中具有不可替代的作用，以往采用有限单元（FEM）网格作为求解基础，计算过程中不可避免地出现网格缠绕或物质界面追踪复杂等问题。光滑粒子流体动力学（SPH）方法是一种无网格数值计算方法，求解过程中不会出现Lagrange网格畸变缠绕及Euler材料界面追踪复杂等问题，适用于爆炸和侵彻等大变形问题的求解。强洪夫等［14］利用SPH方法模拟了聚能装药侵彻混凝土靶板的过程，探究了SPH方法在大变形问题中的适用性。陈杰等［15］基于SPH方法得到了聚能粒子流的演化历程，并将模拟结果与试验进行对比，结果显示SPH方法模拟得到的结果与和试验现象基本吻合。但由于算法差异，SPH方法计算效率较低，且在解决边界条件时存在困难，处理小变形问题时精度也难以保证。基于此，一些学者提出了光滑粒子流体动力学与有限单元（SPHFEM）耦合法，即大变形区域采用SPH粒子，小变形区域采用FEM网格，SPH粒子和FEM网格之间通过耦合算法传递力学信息，模型外侧采用FEM边界约束方法。蔡峰等［16］利用SPH粒子模拟了爆轰产物的流动过程，并将SPH方法与FEM方法耦合得到了爆破裂纹演化历程。胡英国等［17］运用SPH-FEM耦合法求解深孔梯段爆破的动力响应过程，并与现场实测数据进行对比，得出该方法能够准确描述爆破近区的岩体飞散和损伤分布特征。章猛华等［18］基于FEM方法和SPHFEM耦合法模拟了炸药受撞击的响应特性，认为SPHFEM耦合法是模拟炸药撞击响应的最有效方法。Zhao等［19］采用SPH方法、FEM方法及SPH-FEM耦合法模拟了钢筋混凝土板在空气接触爆炸作用下的损伤特性，并与试验结果进行对比，得出：SPH-FEM耦合法用于再现混凝土损伤具有显著优势。王志亮等［20］采用SPH-FEM耦合法模拟了混凝土爆破成坑历程，结合试验数据进行分析，结果表明：SPH-FEM耦合法求解结果与实测数据基本吻合。

现有文献中较少涉及切缝药包爆轰产物的膨胀过程，且有关切缝爆破的数值模拟大多基于传统FEM方法。鉴于此，本研究拟在AUTODYN显式动力分析平台内运用SPH-FEM耦合法建立装药不耦合系数为2.0的切缝药包爆破模型，分析装药爆炸初期爆轰产物的膨胀过程、产物粒子运动速度以及炮孔周围岩体损伤演化历程，以期为切缝药包的进一步推广应用提供理论依据。

2 数值模拟

2.1 数值模型的建立

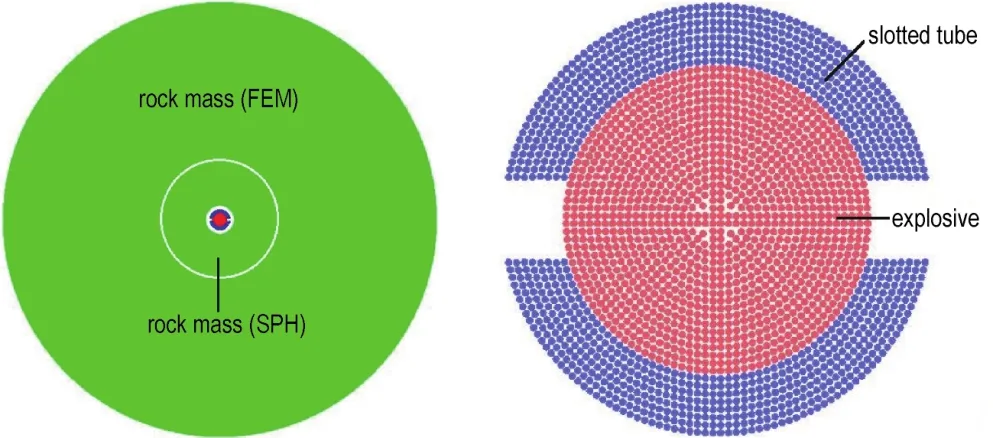
图1 切缝药包爆破数值模型Fig.1 Numerical model of slotted cartridge blasting

由于实际爆破作业中采用柱状装药，装药直径远小于其长度，故在不考虑装药两端特殊爆破效应的情况下，可以将模型简化为平面有限元问题［21］。如图1所示，运用AUTODYN建立切缝药包爆破模型，其中绿色、红色和蓝色分别代表岩体、炸药和切缝管。岩体直径为600 mm，根据文献［22］，炮孔直径为40 mm，药卷直径为20 mm，不耦合系数2.0，切缝管厚度为4 mm，切缝宽度为5 mm，起爆点位于药卷中心。模型各部分均采用Lagrange算法，其中炸药、切缝管及炮孔近区岩体（3倍孔径）采用SPH粒子建模，距炮孔较远的岩体采用FEM网格建模，SPH岩体与FEM岩体之间通过Join功能按钮设置固结耦合。本研究所选装药不耦合系数为2.0，此时空气对爆轰产物膨胀的影响很小，且空气采用欧拉算法无法与SPH进行耦合［23］，因此将空气域视为真空。岩体模型的周围设置无反射边界，以减小应力波反射对模拟结果的干扰。

2.2 炸药与切缝管材料模型

炸药选择梯恩梯（TNT）材料模型，同时使用JWL状态方程［24］精准描述爆轰产物的体积、压力以及能量特性，JWL状态方程决定的爆轰压力为：

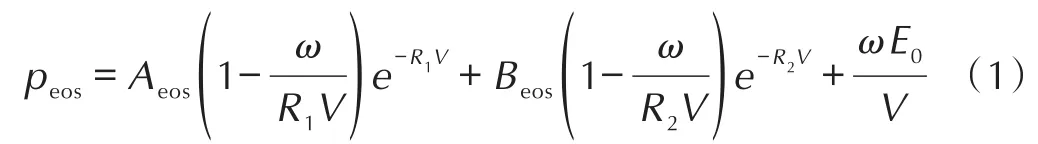
式中，peos为 JWL 状态方程决定的爆轰压力，Pa；Aeos、Beos为炸药材料常数，Pa；R1、R2、ω为炸药材料常数，无量纲；E0为爆轰产物初始内能，J·m-3；V为初始相对体积，无量纲。炸药材料及JWL状态方程参数取自AUTODYN材料库［25］，详见表 1。

切缝管选用不锈钢管［26］，采用 Johnson-Cook材料模型［27］，并同时使用 Shock 冲击状态方程［28］进行描述。Johnson-Cook模型常用于描述材料的大变形、高应变率和高温过程，其屈服应力表达式为：

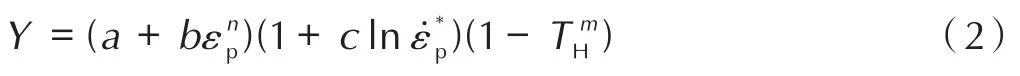
式中，εp为等效塑性应变，无量纲为归一化塑性应变率，无量纲；a为准静态屈服应力，Pa；b为应变硬化系数，Pa；c、n、m为材料常数，无量纲；TH为相对融化温度，K。切缝管材料及状态方程参数取自AUTODYN材料库［25］，详见表 2。

表1 炸药材料及JWL状态方程参数［25］Table 1 Parameters of explosive material and JWL equation of state［25］

表2 切缝管材料及状态方程参数［25］Table 2 Parameters of slotted tube material and equation of state［25］

2.3 岩体材料模型

岩体采用RHT模型，该模型是在HJC模型基础上发展而来的［29］，沿袭了HJC模型具有的压力依赖性、应变率敏感性和压缩损伤软化等特性，并引入拉、压损伤来模拟爆炸载荷作用下岩石等脆性材料的动态响应历程。该模型还引入了失效面、弹性极限面和残余强度面三个控制破坏面，能够较好地描述材料的失效应力、初始屈服应力及残余应力的演化规律［30］。其中失效应力与静水压力p、罗德角θ和应变率有关联，表达式为：

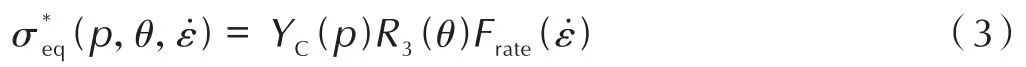
式中，R3（θ）为偏平面上的角偶函数为应变率强化因子；YC（p）为压缩子午线上的等效应力，其表达式为：

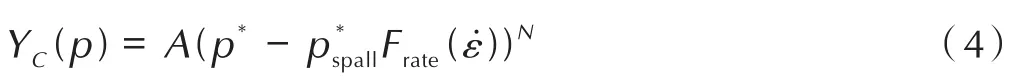
式中，A和N为失效面参数，无量纲；p*为归一化静水压力，无量纲为归一化层裂强度，无量纲；fc为单轴抗拉强度，Pa；pspall为层裂强度，Pa。

此外，引入损伤变量D用于描述残余失效面，损伤变量D定义为非线性偏应变的累积［31］：

式中，εp为塑性应变增量，无量纲；εfmin为材料破坏时的最小塑性应变，无量纲；D1、D2为损伤常数，无量纲。岩体 RHT模型参数取自 AUTODYN 材料库［25］，详见表3。

3 模拟结果与分析

3.1 爆轰产物膨胀过程

基于上述数值模型与材料本构，使用AUTODYN进行求解计算，获得了装药爆炸初期的爆轰产物膨胀过程，并提取出6个不同时刻的爆轰产物飞散形态以及压力云图，如图2所示。为了对爆轰产物粒子膨胀过程进行较为直观的研究，利用后处理中的Axes功能按钮，以炸药中心为原点（0，0）建立x=（-20，20）mm、y=（-15，15）mm的二维坐标系，以便于观测爆轰产物粒子与切缝管在不同时刻的移动位置。此外，还分别在切缝方向和垂直切缝方向由炸药中心向炸药边缘等间距设置3个高斯点，切缝方向高斯点标号为1、2、3，垂直切缝方向高斯点标号为4、5、6，每个高斯点锁定一个SPH光滑粒子，用于追踪爆轰产物粒子的运动速度。

表3 岩体RHT模型参数［25］Table 3 Parameters of RHT model for rock mass［25］

从图2可以看出，炸药首先在起爆点发生爆炸反应并产生爆轰波，爆轰波由起爆点向四周传播，1.5 μs到达药卷边缘完成爆轰过程，此时炸药已经完全发生反应。然后爆轰产物开始由切缝管内部向外膨胀，对于切缝方向，由于没有切缝管的约束作用，爆轰产物粒子能够以较高的速度沿着切缝方向向前运动，3.5 μs时刻最前端的爆轰产物粒子到达炮孔壁，图2f中最前端粒子呈现红色表明爆轰产物作用于孔壁而承受较高的压力；对于非切缝方向，切缝管会产生的较强约束作用使得爆轰产物粒子向外膨胀受阻，且在爆轰产物与切缝管接触界面发生应力波的反射与透射。

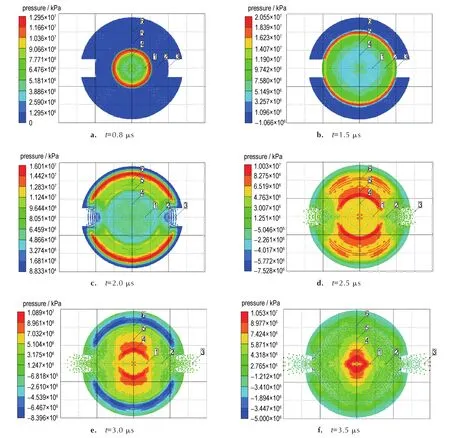
图2 爆轰产物膨胀过程Fig.2 Expansion process of detonation product

在爆轰产物的推动下，切缝管也缓慢向炮孔壁运动，取垂直切缝方向的切缝管外壁坐标进行对比。0～1.5 μs始终维持在（0.00，±14.00），3.5 μs坐标为（0.00，±14.52），可见该阶段切缝管移动距离不到1 mm。

3.2 爆轰产物粒子运动速度

图3是切缝方向和垂直切缝方向各测点的速度-时间曲线。由图3可以看出，当爆轰波在炸药中传播时，爆轰波所到之处会对粒子产生扰动，1号粒子和4号粒子在2.5 μs内具有相同的速度变化规律，2号粒子和5号粒子在2.0 μs内也呈现相同的速度变化趋势，可见切缝管的存在对炸药的爆轰成长过程没有产生影响。

图3 切缝方向和垂直切缝方向各测点的速度-时间曲线Fig.3 Velocity-time curve of measuring points in slit direction and vertical slit direction

根据图3a可以看出，当爆轰产物开始由管内向外膨胀，由于切缝方向没有切缝管的约束作用，3号粒子的速度迅速上升到4000 m·s-1，2.0 μs时刻速度发生下降波动，但又迅速回升且继续上升到4750 m·s-1，并保持该速度向前运动，当3号粒子到达炮孔壁时，粒子速度急剧下降，此后其速度在低值区域不断波动。随着切缝方向边缘处粒子的不断向外飞散，内部粒子开始作为产物粒子流的后续补充，具体则表现为2号和1号粒子速度先后逐渐开始上升，且粒子速度渐趋稳定，基本维持在1000 m·s-1左右。

根据图3b可以看出，由于垂直切缝方向具有切缝管的强约束作用，6号粒子虽然会获得一个运动速度，但其初始速度峰值仅为700 m·s-1。同时爆轰产物与切缝管在边界处发生应力波的反射，向内部传播压缩波，使得6、5、4号粒子的速度按顺序发生进一步衰减，压缩波通过后，三个粒子的速度又都先后开始逐渐回升，4.5 μs以后三个粒子的运动速度基本维持在800 m·s-1左右。

由以上分析可知，切缝方向和非切缝方向爆轰产物膨胀过程、产物粒子运动速度存在明显的差异，这种差异将会对炮孔周围岩体的损伤分布特征产生显著的影响。

3.3 岩体损伤演化历程

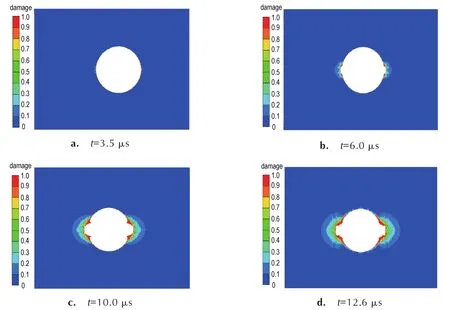
图4 炮孔周围岩体损伤演化Fig.4 Damage evolution of rock mass around borehole

图4所示为炮孔周围岩体损伤演化历程。由图4可以看出，对于切缝方向，由于没有切缝管的约束作用，产物粒子以极高的速度向外运动，形成一股很强的爆轰产物粒子射流，3.5 μs时刻最前端的爆轰产物粒子到达并作用于孔壁，切缝方向的炮孔壁承受较高的载荷开始产生损伤破坏。随着切缝管内爆轰产物的继续膨胀，内部粒子作为产物粒子流的后续补充继续沿切缝方向向前运动，切缝方向岩体进一步受到破坏。文献［7］中，基于FEM方法求解得到了装药爆炸初期切缝方向岩体损伤破坏过程，与本研究所得的现象基本类似，文献［7］中将其描述为“初始裂隙”的演化历程。

对于非切缝方向，由于切缝管的强约束作用，爆轰产物粒子向外运动受阻，在切缝管未能到达炮孔壁之前，爆轰产物无法直接作用于非切缝方向炮孔壁。在爆轰产物的推动下，切缝管也缓慢向炮孔壁运动，12.6 μs切缝管到达孔壁，此时非切缝方向岩体受到切缝管压缩及透射波的作用开始产生损伤，但损伤展布区域较小，且非切缝方向炮孔壁保持较好的完整性。

由于算法自身仍存在一定缺陷，SPH粒子无法与空气Euler网格进行耦合，因此本研究中未能同时考虑空气冲击波对周围岩体损伤演化的影响。但根据以上分析可以看出，采用SPH-FEM耦合法模拟爆轰产物膨胀与装药近区岩体大变形具有独特优势。

4 结论

在AUTODYN内基于SPH-FEM耦合法建立装药不耦合系数为2.0的切缝药包爆破模型，分析装药爆炸初期爆轰产物的膨胀过程、产物粒子运动速度以及炮孔周围岩体损伤演化历程，得出如下结论：

（1）由于没有切缝管的存在，切缝方向爆轰产物粒子能够以较高速度向前运动，最前端粒子在3.5μs到达孔壁；而在切缝管的约束作用下，非切缝方向爆轰产物粒子向外膨胀受阻。

（2）在爆轰产物向外膨胀过程中，切缝方向产物粒子最大运动速度可达到4750 m·s-1，垂直切缝方向产物粒子最大运动速度仅为800 m·s-1。

（3）切缝方向炮孔壁3.5 μs时刻开始产生损伤破坏，随着切缝管内爆轰产物的继续膨胀，切缝方向岩体进一步受到破坏；切缝管在爆轰产物的推动下缓慢向炮孔壁运动，12.6 μs切缝管到达炮孔壁，非切缝方向岩体开始产生损伤，但损伤展布区域较小，且非切缝方向炮孔壁保持较好完整性。