WSN杂交粒子群优化定位改进算法

唐 弢，赵月新，郭 岩，胡福芳

(1. 黑龙江工程学院 电气与信息工程学院，黑龙江 哈尔滨 150050； 2. 哈尔滨云珀科技有限公司，黑龙江 哈尔滨 150000)

定位是无线传感器网络(WSN)中不可缺少的组成部分。定位服务不但可以提供事件发生地的位置信息，而且对于WSN部署以后的其他技术(如路由等)也具有推动作用[1]。目前的定位技术通常分为两类：测距和非测距技术，相对来说测距技术以其定位精度的明显优势得到了更多的青睐，其中，基于RSSI的定位方法更能够满足WSN节点能力的限制要求，因而得到了广泛的应用[2]。

基于RSSI技术中，PSO定位算法及其改进算法以其高精度的特点成为近年来研究热点[3]，其中，最主要的有混合PSO[4]、协同PSO[5]、耗散PSO[6]及杂交PSO[7]等。大多数的改进算法都是在PSO的基础上重新选择或者加入某些参数，亦或是算法策略上的改进。混合PSO定位算法引入了淘汰机制，使其收敛速度(定位时间)大幅度提高，然而该算法基于局部最优的方式，一旦陷入则无法跳出。协同PSO选择了多个子种群同时进行搜索，该算法可以有效避免混合PSO的局部最优问题，然而多个群会导致计算量过大，无法满足WSN节能的要求[8]。杂交PSO利用杂交方式通过父代粒子产生子代粒子，两者数量相同，并且能够利用扰动因子，避免全局最优和早熟现象的发生，同时相比于其他改进算法具有良好的定位精度和收敛性[9]。因而，利用杂交PSO算法在WSN对未知节点进行定位相对广泛。然而，杂交PSO定位算法仍然存在计算量大、定位时间长等问题。

1 WSN杂交粒子群优化定位改进算法

杂交粒子群优化定位改进算法流程如图1所示。

1.1 选择机制

如图1所示，每个粒子计算适应值并更新个体极值pBesti和全局极值gBest[10]

pBesti(k+1)=

(1)

f[gBest(k+1)]=

min{f[pBesti(k+1)]},i=1,2,…，N.

(2)

更新后需要判定是否终止， 若不满足终止条件则需进行选择操作。如图1所示，选择机制的原理就是通过引入粒子集中度gath(k)和粒子平稳度smth(k)两个概念，判定是否进行交叉和变异。粒子集中度gath(k)和粒子平稳度smth(k)分别定义为

(3)

(4)

式中：M为种群数量；S为平稳阶数；C为任意常数。通过计算可知，粒子集中度gath(k)和粒子平稳度smth(k)的范围均为gath(k)∈[0,1]，smth(k)∈[0,1]。

当集中度gath(k)趋近于1时，表示在k时刻，粒子的分布相对集中，此时定义不需要进行交叉操作；反之gath(k)趋近于0时，则需要进行交叉操作。

当平稳度smth(k)趋于1时，表示k时刻粒子以相对较低(趋于0)的速度运动，在此情况下陷入局部最优解的可能性加大，因而需要进行变异操作跳出局部最优解；反之smth(k)趋近于0时，则不需要进行变异操作。

定义某数值α,β作为阈值来判定是否进行交叉和变异操作，其中,α，β∈ [0,1]，具体数值可以在试验中通过经验测定得到。

因而，选择机制可以描述为

1.2 交叉与变异

交叉与变异的方法与杂交PSO相同，算法原理如图2所示[11]。

假设p1(xid)/p2(xid)、p1(v)/p2(v)和ch1(xid)/ch2(xid)、ch1(v)/ch2(v)分别为父代和子代粒子的位置、速度。

交叉过程可以用公式表示为

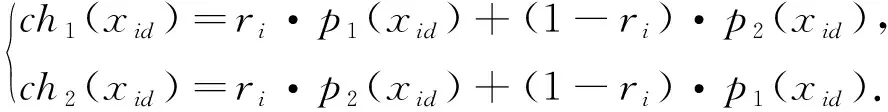
(5)

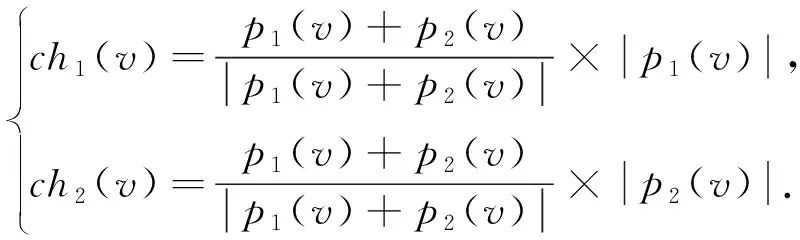
(6)

式中：ri为在[0,1]区间内均匀分布的随机数。

变异过程的实施目的是为了跳出局部最优解，即在传统PSO中加入扰动因子，从而避免PSO的停滞现象。

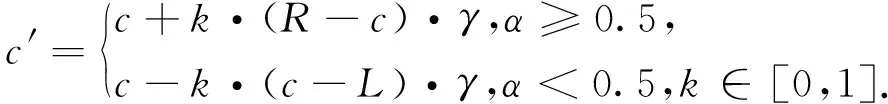
(7)

式中：[L,R]为参数变化范围；α，γ∈[0,1]且随机分布。

交叉变异的特点及优势主要体现在：子代粒子可以最大限度地保留父代粒子的优点，且数量与父代粒子数量相同，因而随着迭代次数的增加，粒子的相似度不断增大；加入扰动因子后可以有效地避免早熟现象及后期相似度增大所带来的局部最优问题。

将粒子集中度gath(k)和粒子平稳度smth(k)应用于交叉和变异过程中以后，可以通过计算和预判精准控制何时实施交叉，何时实施变异，这大大地提高算法收敛性和定位时间。通过多次试验可以看出，一般交叉操作发生在迭代初期，而变异操作发生在迭代后期。

1.3 排队机制

在传统PSO中，每一个粒子以各自的适应度函数判断目前位置是否为最优位置。适应度函数为

(8)

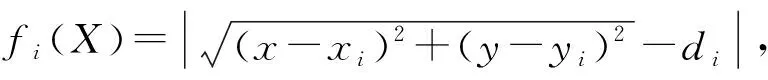
为了获得更优良的子代粒子(子代粒子可以保留父代粒子的遗传性)，在算法中引入排队机制。将父代粒子的适应值进行排队，选取最优的一部分作为父代，再以交叉概率pc进行杂交，从而保证杂交过程的目的性和方向性。具体实施时间节点如图1所示。

2 算法仿真

2.1 仿真环境

仿真环境为空旷的方形场地，其边长为50 m×50 m。在方形网络中，设置未知节点20个，锚节点(自身位置已知，且能主动定位)5个，节点通信半径为70 m，即节点可以覆盖整个方形区域。每个节点都具有RSSI装置，其测距误差为0～30% ，节点发射功率0.25 mw，发射频率2.4 GHz。锚节点及未知节点均随机分布，每一次仿真的结果是20个未知节点中可定位节点的平均值。

PSO算法的种群数量为50个，学习因子c1=c2=2，惯性常数ω采用线性递减法，且ω∈[0.4,1.0]，即选择由1.0到0.4的线性递减模型。迭代终止条件满足精度10-6或者达到最大迭代次数Tmax=100。

2.2 仿真结果和分析

2.2.1 定位效果

通过仿真，IHPSO定位效果如图3所示。

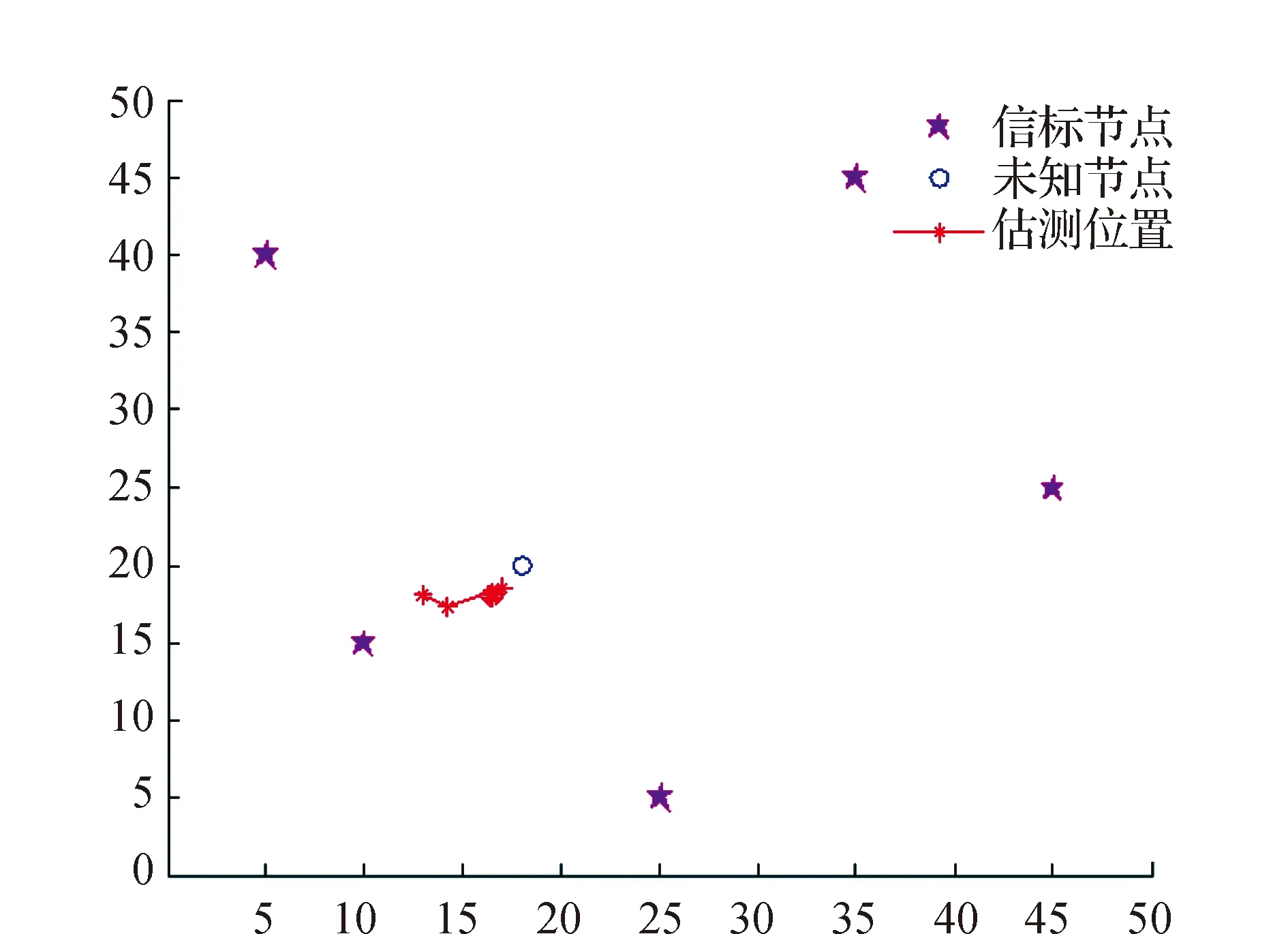
(a)迭代过程

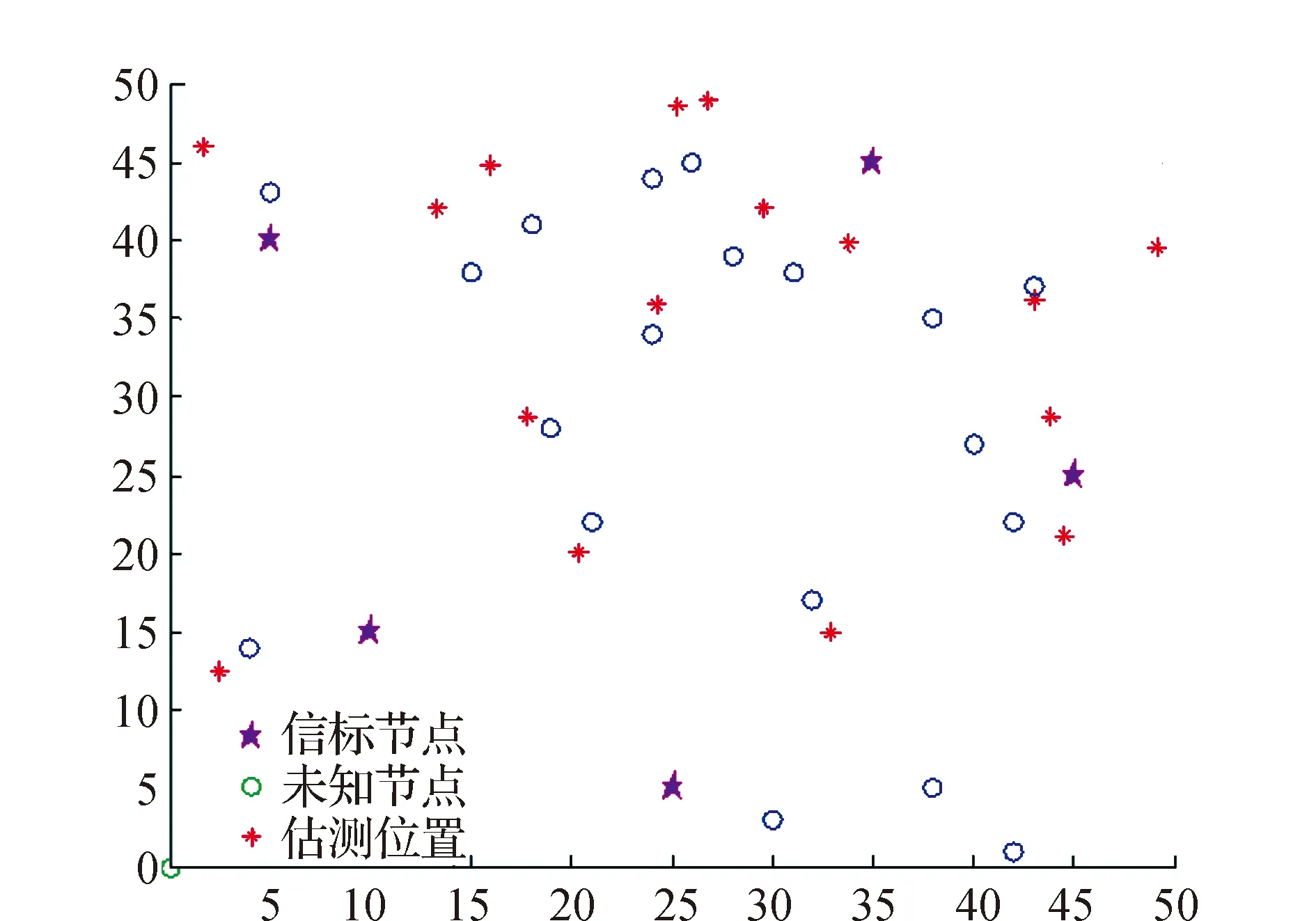
(b)最终效果(n=2.5，N=40，Tmax=100)图3 IHPSO定位效果

图3(a)为对区域中的某一节点定位过程的动态迭代效果，图3(b)为对区域中所有节点实施算法后的定位效果。从图3(a)可以看到，IHPSO在迭代过程中，估计节点位置始终朝着节点的实际位置逼近，随着迭代次数的不断增大，估计节点位置与实际节点位置之间的距离越来越小。图3(b)是连续仿真10次以后的平均定位结果。通过IHPSO算法实施，对区域内20个节点中的16个能够有效定位，且定位误差为6.47%，即平均误差距离为3.2 m。

2.2.2 定位误差

本文通过改进杂交PSO算法，达到降低定位误差的目的。将errorL定义为定位误差，errorL是估测节点坐标与真实坐标的距离，与测量范围边长的相对值，记作errorL。

在IHPSO算法中，通过调整路径损耗指数n、种群数量N和迭代次数T等指定参数，对IHPSO算法进行多次实验，并与传统PSO、杂交PSO算法进行对比，从而达到降低errorL的目的。仿真结果如图4所示。

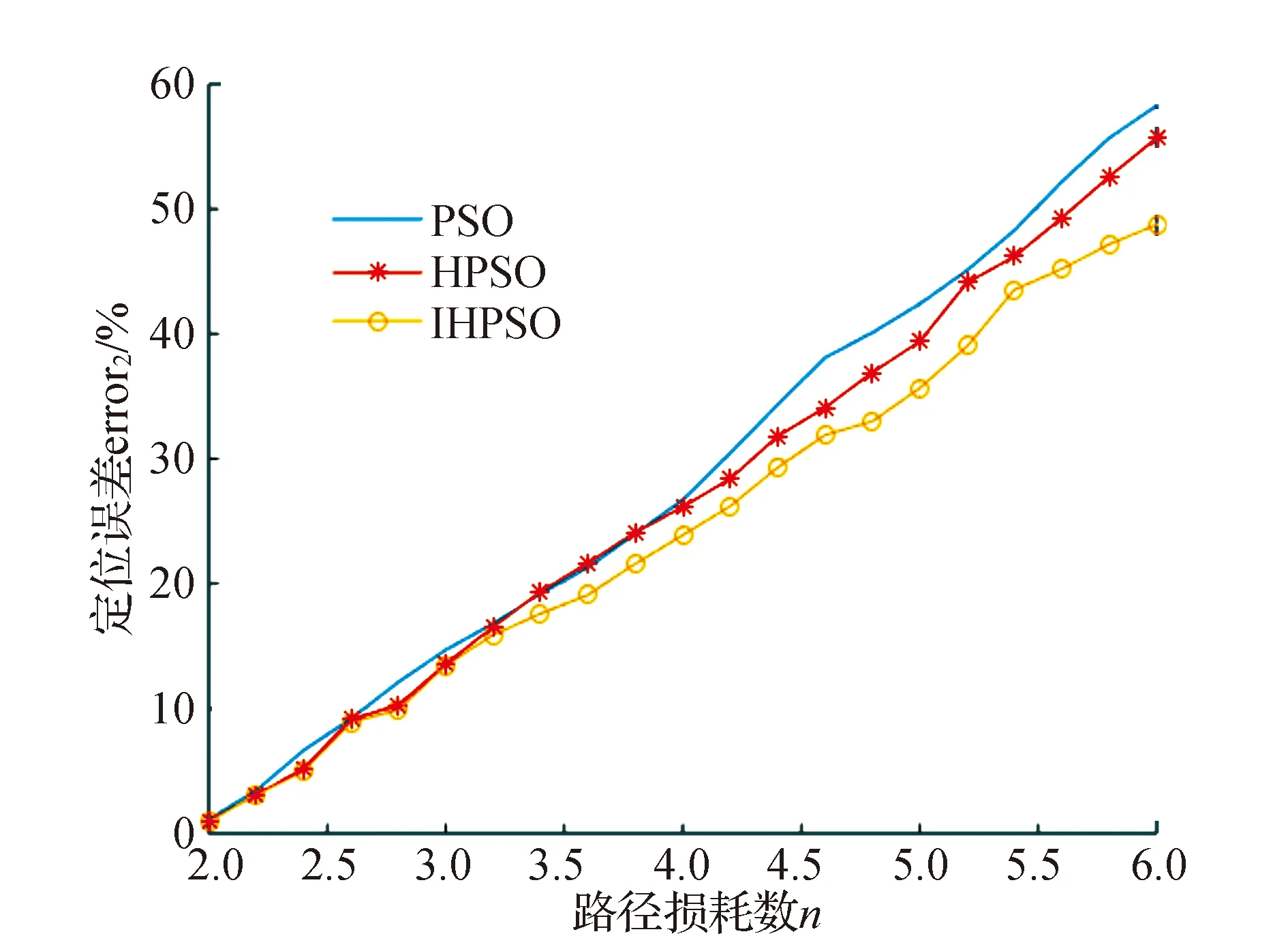
图4 路径损耗指数n对定位误差的影响

从仿真中可以看到：首先，在路径损耗增大的情况下，相应的定位误差errorL也随之增大，这符合定位的一般规律；另一方面本文提出的IHPSO算法无论是对比传统PSO还是杂交PSO，在n=2～6时，errorL均有所改善，特别是n值较大时，改善更为明显。

对算法进行多次仿真(连续10次仿真求平均值)，对比纵向结果可以看到：当路径损耗系数变化时，杂交PSO优于传统PSO的定位误差，平均降低5.44%；而在杂交PSO基础上改进的IHPSO算法相比于杂交PSO的定位误差errorL平均降低了6.9%；与传统PSO相比则优势更为明显，平均定位误差降低了12.9%。

另外，当路径损耗逐渐增大时， IHPSO对errorL稳定度的改善更为明显，在10次重复性实验中，当n=5时，PSO、杂交PSO及IHPSO的方差(定位误差偏离度)分别为180.9、169.5及74.36；当n=6时分别为386.5、428.2及190.4。

综上所述，IHPSO算法在定位误差及定位的稳定度上，相对于原有的PSO及杂交PSO都有所改善，且随着路径损耗的增大，改善更为明显。另外，除路径损耗指数外，种群数量、迭代次数等均会对仿真结果造成一定的影响，这里不再赘述。

2.2.3 定位时间

定位时间是评价算法的重要指标之一，一般来说定位时间越少，更适用于无线传感器网络，算法的应用范围也就越广。3种算法对定位时间的仿真如图5所示。

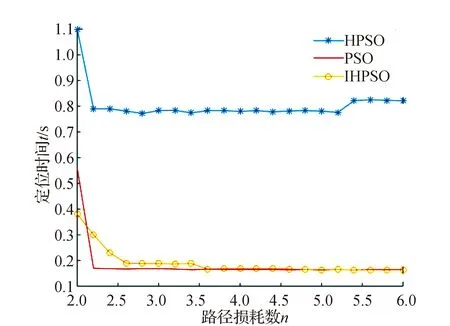
图5 3种算法n与t

图5反映了路径损耗与定位时间的关系。可以看出，杂交PSO的定位时间明显高于传统PSO，而由于加入了排队机制和选择机制，IHPSO的定位时间虽略高于传统PSO，但相比于杂交PSO有大幅度的降低。此外，定位时间还与最大迭代时间、种群数量有关，显然，当N，Tmax增加时，定位时间将大幅增大。将3种算法横向比较：当n=2，N=50，Tmax=100时，QJ-CMPS平均定位时间0.3 s，HPSO 0.9 s，IHPSO一次定位时间降低了66.7%。

3 结束语

本文将选择机制和排队机制引入杂交PSO中，提出一种WSN杂交粒子群优化定位改进算法(IHPSO)，该算法可以计算和控制发生变异和交叉的时间，有效利用子代与父代之间的遗传性快速收敛，并且能够通过加入扰动粒子避免早熟现象的发生。实验证明，该算法可以有效地提高传统PSO和杂交PSO算法的定位精度和定位时间。