基于Kriging代理模型的异形钢桁架桥有限元模型修正

丁曦，王佐才,2

（1.合肥工业大学土木与水利工程学院，安徽 合肥 230000 2.土木工程防灾减灾安徽省工程技术研究中心，安徽 合肥 230000）

0 前言

近些年，有限元分析得到广泛应用，但是由于受到有限元模型的网格划分、边界条件和材料物理参数等不确定性因素的影响，建立的有限元模型与真实结构始终存在一定的差异，因此需通过试验数据加以修正，使其尽可能接近实际结构。

关于有限元模型修正的方法可以分为三类，即直接类修正算法[1]、迭代类修正算法[2]和基于智能优化技术的修正算法[3]。直接类修正算法是从结构振动微分方程出发，通过直接修改结构刚度与质量矩阵中的元素达到模型修正的目的，但由于修正后的参数物理意义不明确，此类方法已不常用。迭代类修正算法目前主要运用在非线性结构问题中，在实际选择参数方面会更加的灵活，但是在实际运用过程中存在计算量巨大的问题无法解决。

在实际运用有限元模型计算的过程中，由于直接调用有限元软件进行模型修正存在着计算效率低、不方便二次开发等缺点，学者提出了采用代理模型并结合智能算法进行模型修正的方法，此类方法可以克服修正过程中大量调用有限元模型计算繁琐的不足。目前常用的代理模型包括响应面模型[4]、径向基函数模型与Kriging代理模型等。

其中，Kriging代理模型方法[5]也称空间局部估计法，由南非地质学者Krige于1951年提出，最初是用来确定矿产储量分布。Sacks[6]等第一次将Kriging方法应用于结构设计。Rom ero[7]等将其应用于求解结构可靠度问题中。Kriging代理模型是一种半参数化的插值模拟建立模型的方法，考虑设计变量在空间上的相关特性，利用某一点周围信息模拟某一未知点的响应等信息[8]。

本文以滨湖路钢桁架桥为研究对象，选择桥梁结构的参数作为修正对象，基于Kriging代理模型和桥梁荷载试验数据，以修正桥梁的有限元模型，使有限元模型更接近桥梁的实际情况。

1 Krig ing模型修正理论

1.1 Kriging模型

Kriging模型方法作为线性回归分析的改进技术，由线形回归模型与随机过程相加组合而成，其基本形式为：

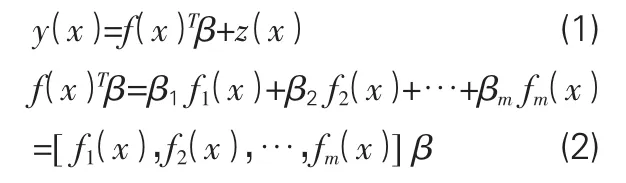
式中：x是维度为d的设计参数[x1，x2，…，xd]；y（x）为多项式模型；z（x）为正态分布函数，其不独立但同分布；f（x）为类似响应面模型，可以根据需要选择零阶、一阶及二阶多项式，m是多项式的数目。

f（x）负责模拟全局近似计算，z（x）负责模拟局部近似计算。z（x）是随机过程，其均值为零且协方差不为零。在Kriging代理模型中，由于z（x）这一随机过程的灵活运用，其建立的代理模型具有很强的灵活性，这样一来，模型可以更好的运用于求解复杂情况的非线性结构，解决了传统基于多项式函数所建立的代理模型在精度上的不足。

z（x）的协方差矩阵具有如下形式：

式中：

R[R（ xi，xj）]为ns个样本点中，任意两个点xi、xj间的空间相关函数，其对模型的精度有主导作用，其核函数具有多种形式可以选择，在实际运用过程中，高斯函数通常可以得到较好的计算结果，其形式如下：

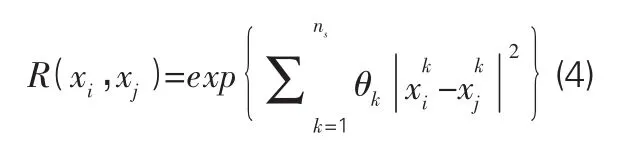
1.2 Kriging模型参数的确定

对于参数θk的估计，通常用已知结构响应的线性组合来估计，引入以下矩阵：

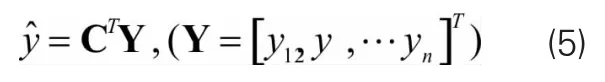
由上式可得出结构响应估计值的残值：

若上式所示残差的平均值为0，则得到的结构响应值则为无偏估计值，可得到下式所示关系：

可以求得结构响应估计值的方差为：

式中：r为相关矩阵R中的某一列。通过求解结构响应估计值方差的最小值，并使其满足无偏估计的约束，可建立优化目标函数：

式中：λ为拉格朗日乘子向量，通过优化求解可得以下结果：

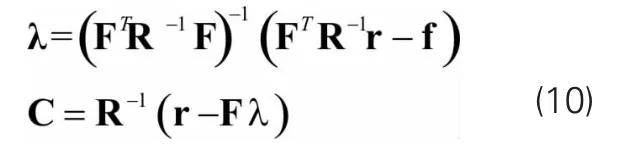
将上述结果引入结构响应估计值可得：

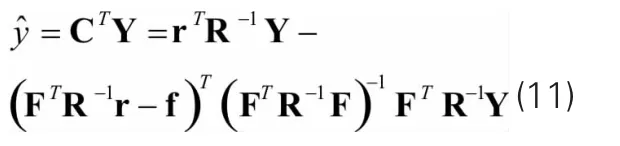
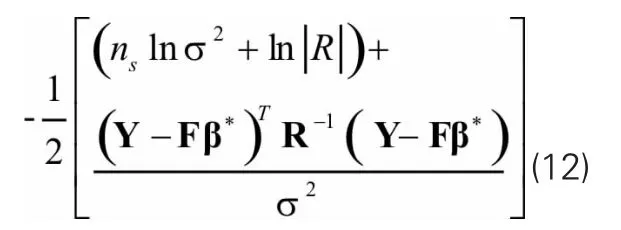
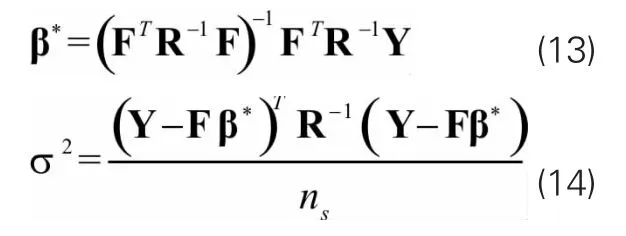
式中：空间相关矩阵R为：

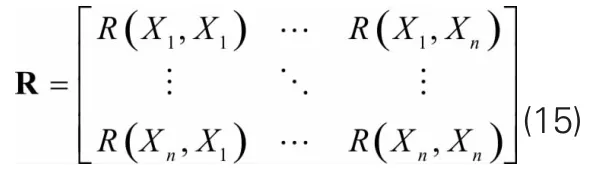
上述两式β*与σ2均是参数θk的函数，通过极大似然估计使拟函数取得极大值为：

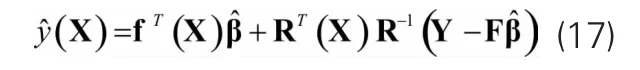
求解关于以上优化问题，可得到参数θk的估计值，即可建立Kriging模型。

基于Kriging模型的有限元模型修正方法也属于响应面方法的一种，通过不同函数建立的响应面模型其适用性也不尽相同，所以，就需要对所建立的响应面模型进行精度验算。验证响应面模型精度的方法有很多，如：残差的正态分布检验、残差的均值、EISE检验、R2检验[10]及相对均方根误差(Root Mean Squared Error)[9]检验方法。在较为复杂的模型中，R2检验和相对均方根误差(RMSE)检验可更好的检验模型精度。其数学表达式如下式所示：

相对均方根误差(RMSE)：

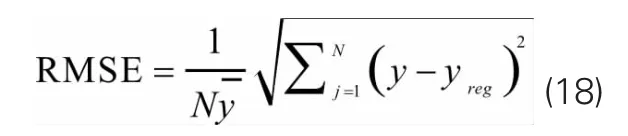
判定系数：

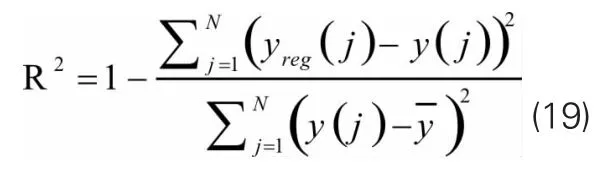
式中：

y和yreg分别是设计空间上各点的真值和响应面模型的值为设计空间上各点真值的均值；N为设计空间上检验点的数量。相对均方根误差(RMSE)的大小R2代表了响应面的精度，可根据实际情况确定，其值越接近0则表示响应面模型越精确。代表了响应面与真值之间的差值，其值在0～1之间，当其值为1时，表示二者完全一致。

2 初始有限元模型建立

2.1 桥梁概况

滨湖路桥位于宛溪河上，其主体结构为两跨钢桁架桥其跨径为50+50m，主桁架采用双片桁架，边支点桁高为4.5m，中支点桁高为 17.5m。上弦杆线形为二次抛物线形式，主桁架下弦杆采用焊接整体节点结构形式，主桥桥梁横断面共33m，全桥材料为Q345qD钢材。

桥型布置如图1所示。

图1 滨湖路桥桥型布置图

2.2初始有限元模型的建立及计算结果

按照设计图纸，使用有限元计算软件M idas建立全桥有限元模型，上部结构采用Q345qD钢材，设计强度200MPa，容重取，考虑到加劲肋、横隔板、横肋的重量，桥梁结构的自重系数取1.2。每侧护栏取，每侧灯柱取，桥面铺装取，人行道自重简化成荷载：，人群荷载集度取：，汽车荷载取公路-Ⅰ级。

桥面系模型采用4片主梁，主桁架采用双桁架模型进行分析，全桥模型均采用梁单元进行模拟。全桥共离散成1112个单元。其有限元计算模型见图2所示。

图2 全桥有限元计算模型

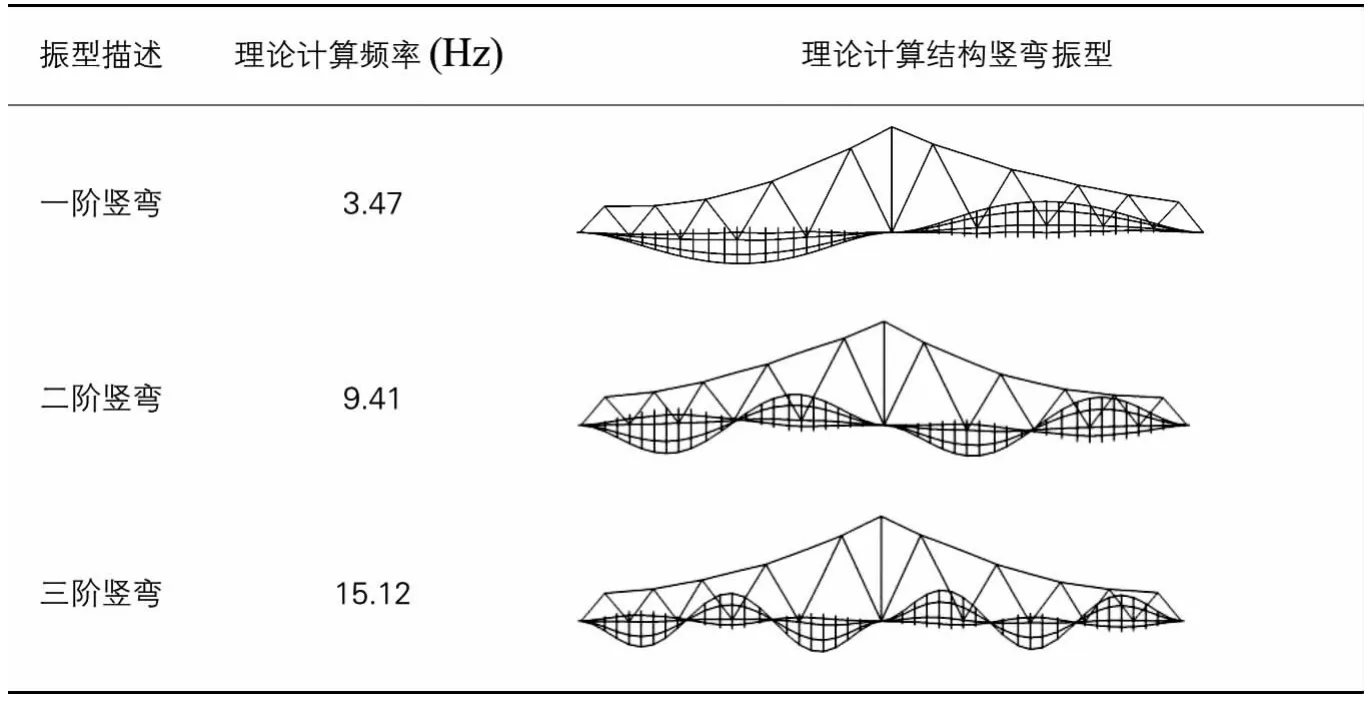
滨湖路桥理论计算自振频率与振型 表1

表1给出利用有限元模型计算得到的结构前三阶竖弯自振频率与振型。

3 现场脉动试验及结果

3.1 脉动试验内容

脉动试验主要测量主桥的自振频率、振型和阻尼比。试验选用压电式加速度传感器，记录桥梁结构在环境激励下，如风、水流、地脉动等引起的桥梁振动，然后对记录下来的桥梁振动时程信号进行处理,并进行时域和频域分析，求出桥梁结构自振特性。全桥共设置6个加速度传感器测点，试验中加速度传感器测点布置如图3所示。

对环境激励下桥梁的响应信号进行多次功率谱的平均分析，可得到桥梁的各阶自振频率，再利用各个测点的振幅和相位关系，可求得桥梁各阶模态相应的振型，利用幅频图上各峰值处的半功率带宽或时域上的自相关确定各阶模态阻尼比。利用脉动试验测出全桥结构前三阶竖弯振型以及频率。

图3 全桥脉动试验测点布置图

3.2 脉动试验结果分析

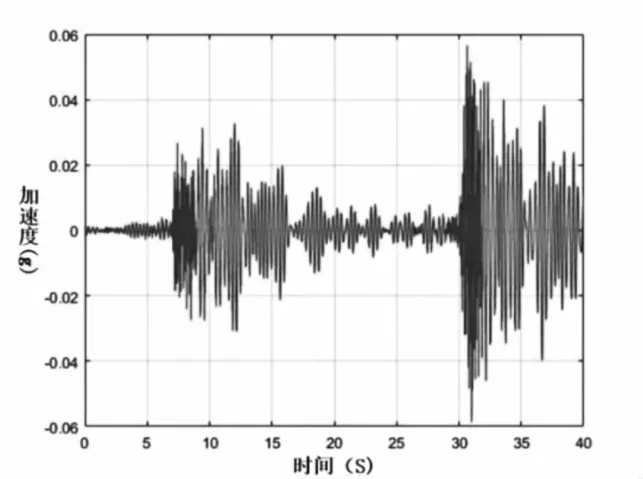
图4 1号测点加速度时程响应

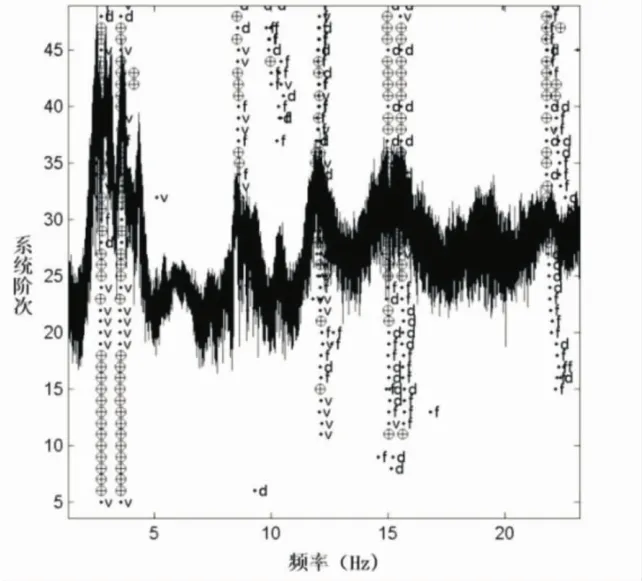
图5 基于SSI的竖向振动频率稳定图

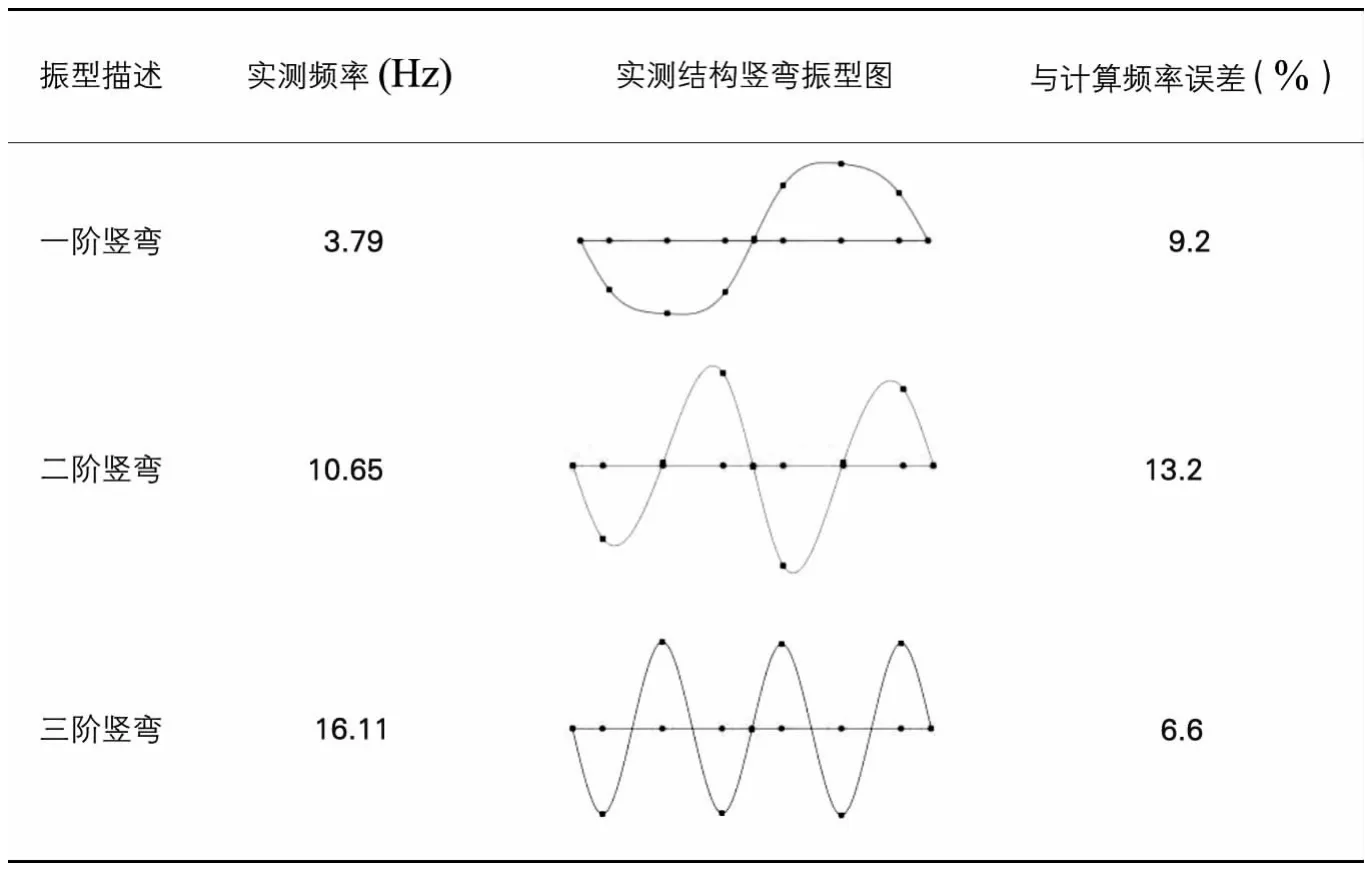
滨湖路桥自振频率与振型实测结果 表2

相关参数的初始值 表3

本文中，使用随机子空间方法(SSI)方法，处理所采集的响应信号，识别结构的模态参数。图4为1号测点的加速度时程响应。图5为基于SSI的竖向振动频率稳定图。表2列出了该桥实测自振频率以及振型图。

4 有限元模型修正

4.1 Kriging代理模型建立的试验设计

利用Kriging代理模型进行有限元模型修正，即通过隐式函数关系来表示随机输入变量与输出变量之间的关系，并采用相关试验来拟合假定的函数关系，利用其替代原复杂结构的有限元求解过程。基于Kriging代理模型来进行有限元模型修正通过四个步骤来实现：①试验设计，设计一定的试验方案，确定结构的输入与输出信息；②确定Kriging模型的回归模型与相关模型函数的具体形式；③建立代理模型，通过相应的数据拟合出响应面模型，并检验模型的拟合精度；④优化与预测，利用实测响应值与参数通过Kriging模型进行分析与预测，得到优化后的结构参数以及其对应的有限元模型。

基于上述理论，首先对桥梁脉动试验进行分析，选定滨湖路桥结构相关参数作为修正影响因素分析。本文，选取结构的弹性模量、泊松比、线膨胀系数与容重作为需要修正的影响因素。选取结构的各参数的初始值如下表所示，在此基础上，选择相关参数变化空间为初始参数的0.75～1.25倍。表3为相关参数的初始值。

本文基于均值设计，样本设定为U12（124），即4参数，12组样本。表4和表5为12水平均匀设计表与12水平均匀设计表的使用表，均匀设计法可以很好的将参数分布在整个设计参数空间内，并且可以大大地减少试验次数。

根据表6与表7均匀设计表及其使用表，设计如下12组Kriging代理模型试验。

根据12水平均匀设计表及其使用表格，设计各组试验，一共12组，通过改变设计的参数，利用建立的有限元计算模型，得到所需频率值，其结果如表7所示。

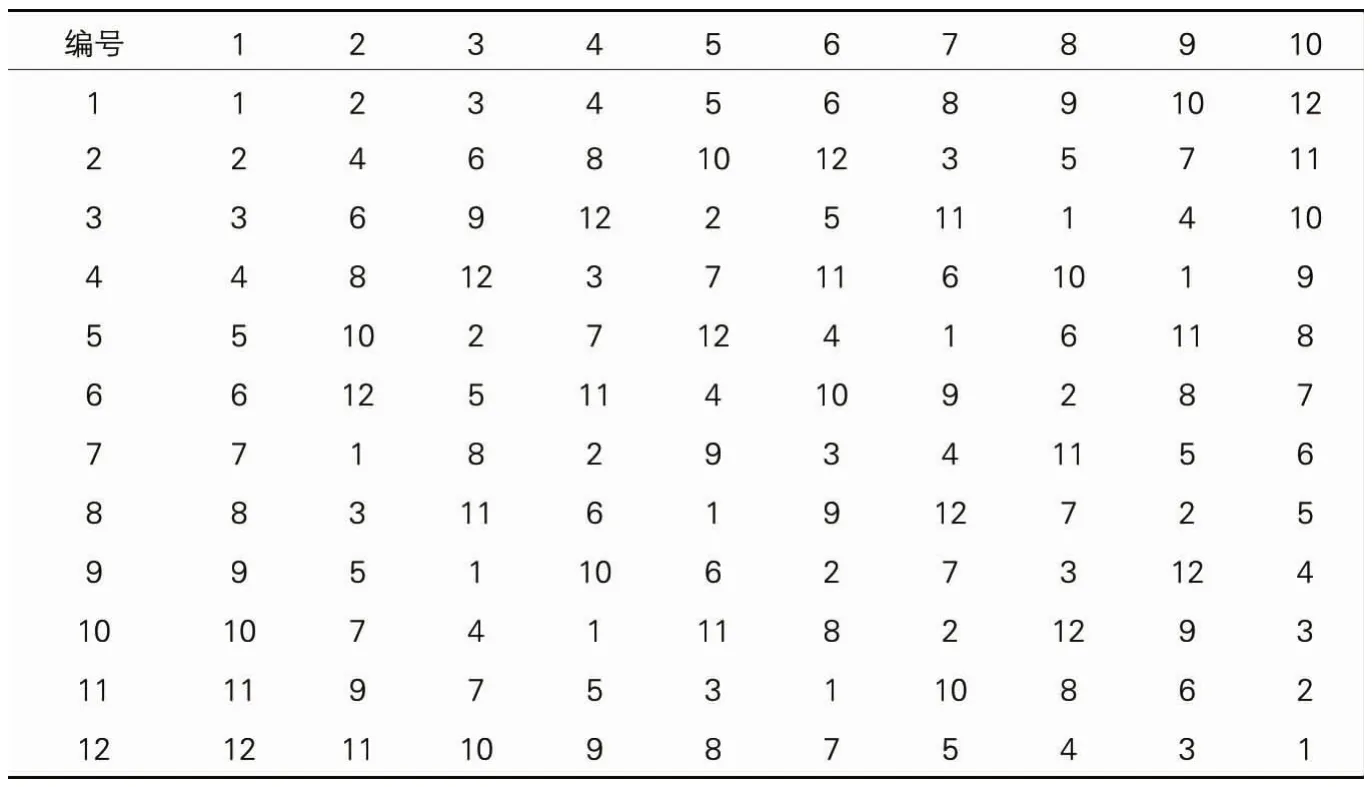
12水平均匀设计表 表4

12水平均匀设计表使用表 表5

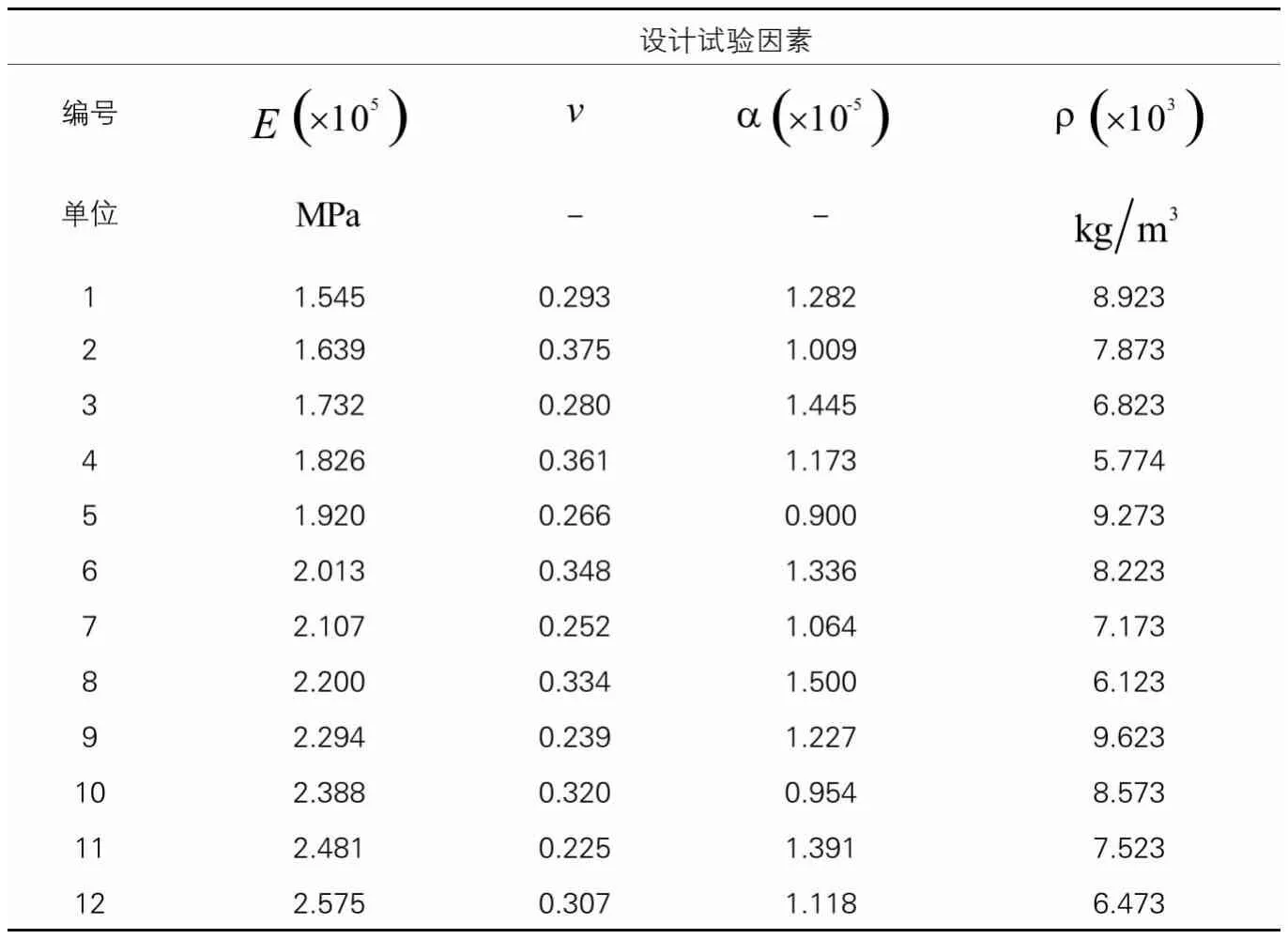
Kriging代理模型试验设计 表6

4.2 代理模型的建立

通过上述均匀设计的样本点作为已知信息输入矩阵；将有限元计算软件得到的相应频率值作为输出矩阵。由于实际工程问题中非线性问题程度较高，本文中回归模型选用线性函数；对于相关函数方程的选择，由于高斯函数相对于其他几种相关函数优化模型的优化效果最好，本文中相关函数选用高斯函数。

运用M atlab软件中的DACE工具箱构建Kriging代理模型，本文中，采用粒子群优化算法对参数进行优化，用确定的参数确定最优相关模型。

基于Kriging理论所建立的代理模型为一个隐式函数，在本文中不给出具体的函数表达式，仅以响应面图形表示所建立的Kriging代理模型。图6～图8分别表示各主要结构参数与前三阶固有频率值之间的Kriging模型。图(a)为弹性模量和泊松比分别与前三阶固有频率之间的Kriging模型，图(b)为线膨胀系数和容重与前三阶固有频率之间的Kriging模型。

将前三阶实测频率输入构建的Kriging代理模型中用于回归预测，便可得到预测值，将预测所得的设计参数代入原有限元模型中以达到修正此有限元模型的目的。通过求解修正后的有限元模型便可得到修正后的理论振动频率。预测参数值如下表8所示，表9给出了通过Kriging代理模型修正后的理论振动频率与实测振动频率以及修正前的原始有限元模型计算所得振动频率。

由表9可知，经Kriging代理模型修正后计算所得结构频率与真实值相差均在以内。

4.3 Kriging代理模型精度检验

验证Kriging代理模型所得预测值的精度，本文引入前文所述的检验及相对均方根误差(RMSE)对修正后的模型进行评估。表10表示了所建立的Kriging代理模型的精度计算值。

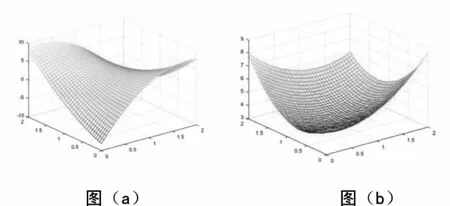
图6 各主要参数与第一阶固有频率Kriging模型

图7 各主要参数与第二阶固有频率Kriging模型

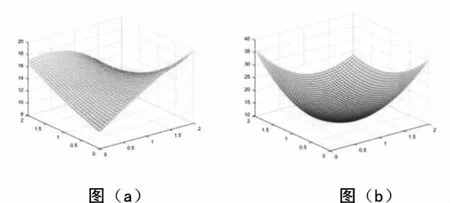
图8 各主要参数与第三阶竖弯频率Kriging模型

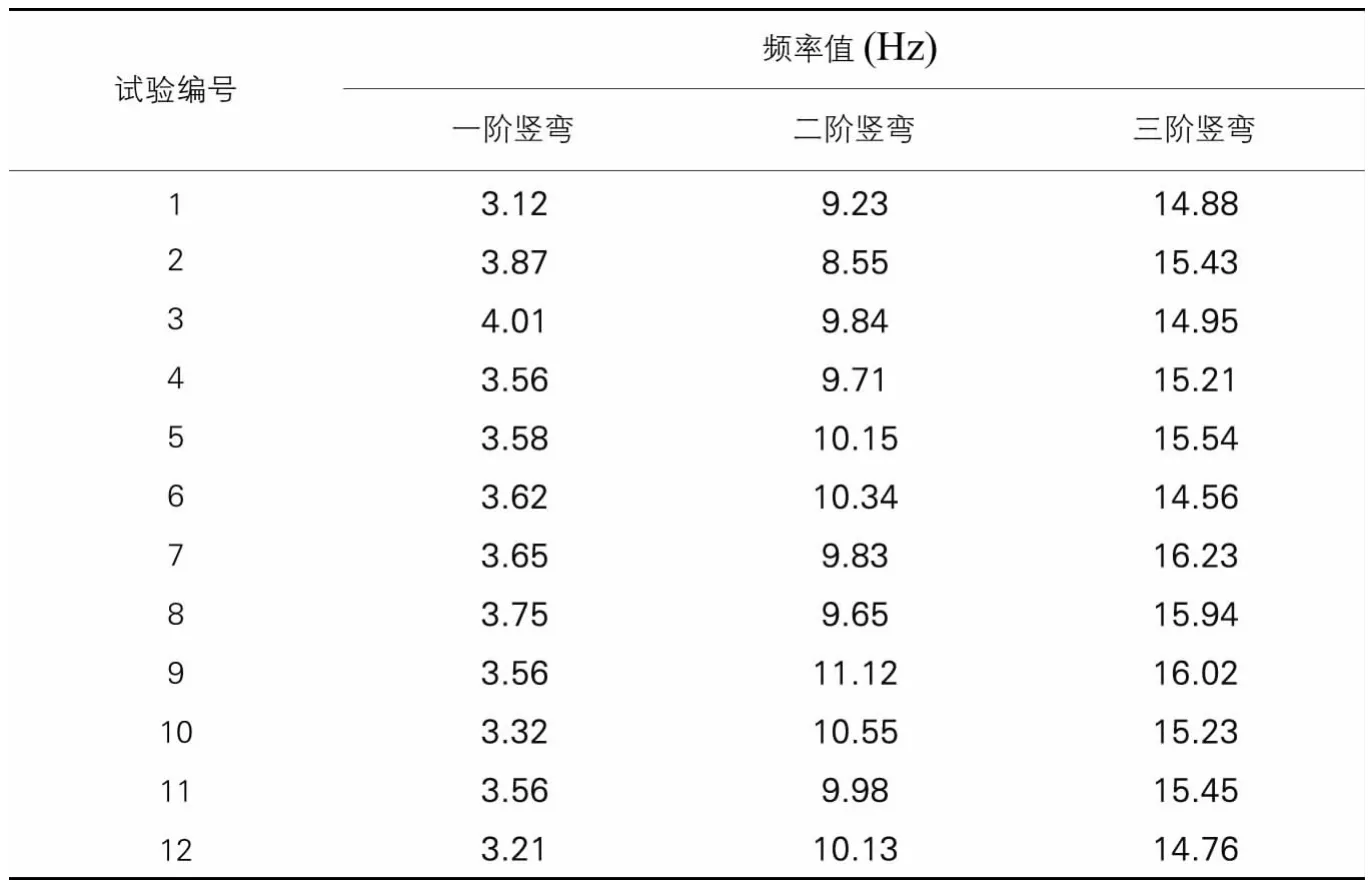
设计试验所得频率值 表7

经Kriging代理模型修正后的参数值 表8

实测频率与修正前后频率结果对比表 表9

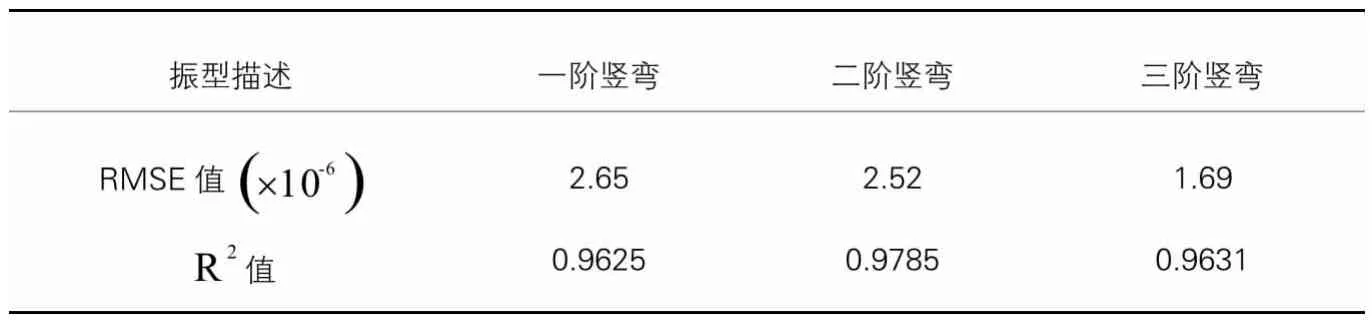
各阶次Kriging代理模型精度分析 表10

从上表可知，相对均方根误差(RMSE)值均很接近0，这表明所建立的Kriging代理模型与有限元模型计算值之间的差异很小；在值计算中，各阶次的Kriging代理模型精度的计算结果均在0.95以上，这表明建立的Kriging代理模型可以准确地描述系统输入与输出之间的关系。此时建立的Kriging代理模型已经可以很好的进行有限元参数优化。

5 结论

本文介绍了Kriging代理模型在有限元模型修正中的应用，并通过滨湖路桥实例说明Kriging代理模型结合有限元软件在桥梁工程中的实际应用。

①举例说明Kriging代理模型在桥梁工程中的具体应用，利用实际测量的桥梁结构动力特性去修正桥梁实际的结构设计参数，并验证了修正后参数的具体物理意义；

②验证了利用桥梁荷载试验，建立Kriging代理模型优化原有限元模型方法的可行性，这种方法可以减小桥梁试验对原桥梁结构的影响；

③通过对既有桥梁进行预测并与实测结果对比，结果表明，修正后的有限元模型可以更好的反映桥梁结构的真实情况。