蒸发波导条件下风速风向对电磁波传播的影响

姚忠山，焦 林

（海军大连舰艇学院 军事海洋与测绘系，辽宁 大连116018）

为提高近海沿岸的预警监视能力，需要准确评估和预报雷达系统的探测性能，而雷达探测能力的预报取决于雷达各项技术参数和传播介质，目前已有多种方法能够模拟雷达电磁波在大气中的传播。当然电磁波模拟还依赖于传播区域的特征参数：海面有无大气波导、海表特征参数等。

蒸发波导是发生在海面上的一种异常折射现象，主要是由于海水蒸发引起湿度锐减造成的。其中风向、风速是影响蒸发波导形成及其强度的重要因素，对电磁波传播有着显著影响。国外O Benhmammouch 等[1]研究了蒸发波导条件下粗糙海面对电磁波传播的影响，提出了一种风向对海面生成的方法。K H Craig 等[2]利用抛物线方程模型模拟了雷达电磁波的传播。刘勇等[3]分析了粗糙海面对电波传播的影响，潘越等[4]研究了粗糙海面对微波蒸发波导超视距传播的影响，得到粗糙海面的反射是计算微波沿粗糙海面蒸发波导传播路径损耗不可忽视的重要因素。本文在前人研究的基础上，利用抛物线方程模型，结合海面粗糙度参数和蒸发波导条件下大气修正折射指数廓线模型来求解电磁波波动方程，基于电磁波传播的数值模拟结果，重点研究蒸发波导条件下风速和风向对电磁波传播的影响，主要工作体现在两个方面：一是利用抛物线方程的裂步傅里叶算法来数值模拟电磁波的传播，重点考虑传播区域中传播介质[5]（蒸发波导环境等）和海面粗糙度对电磁波传播的影响；二是研究蒸发波导条件下风速和风向对电磁波传播的影响[6]。

1 蒸发波导条件下电磁波的传播

1.1 电磁波传播模型

引入抛物型方程来计算电磁波在大气中的传播，这个方程被定义在圆柱坐标系中:

式中：x为电磁波传播方向；z为高度；k为波数；m为大气修正折射指数；u(x,z)为由参考文献[7-8]给出的衰减函数，可表示为：

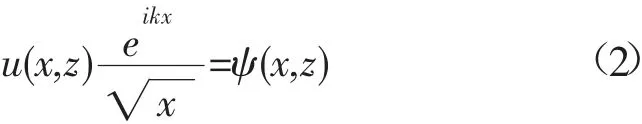
式中：Ψ 是电场或磁场。

为了求解式（1），可以结合准确的边界条件和初始值，利用步进类型的数值方法求解，目前普遍的做法都是使用裂步傅里叶（SSFA）算法[7，9]来求解电磁波传播方程。

已知x0的解u(x0，z)，对其进行傅里叶变换，得到：

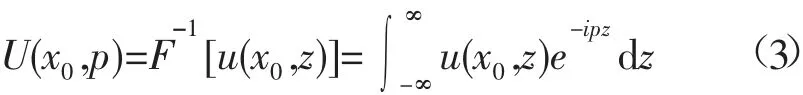
式中：F代表傅里叶变换；F-1代表傅里叶反变换；p=ksin(θ)，其中θ 表示波速指向角。

对于距离增加δx量的解为：

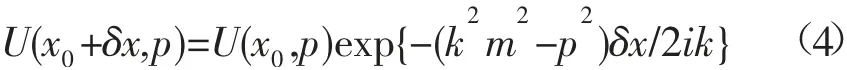
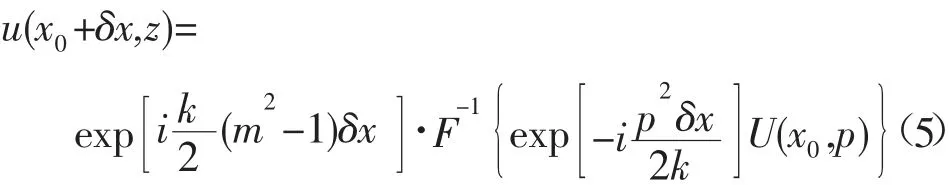
对式（4）进行傅里叶反变换，得到：同理，可以得到u(x0+2δx,z)，u(x0+3δx,z)，…的解，当m为常数时，式（5）是式程（1）的确切解。

1.2 蒸发波导环境的影响

在对流层大气中，电磁波的传播会受到很多参数的影响，其中大气折射指数n是最重要的一个。利用Smith 和Weintraub 模型[10]所确定的大气折射指数计算式如下：

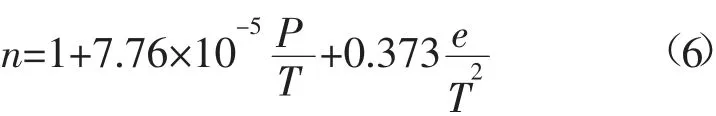
式中：P为大气压强，hPa；T为大气温度，K；e为水汽压，hPa。

为消除地球曲率的影响，引入大气修正折射指数m[10-11]：

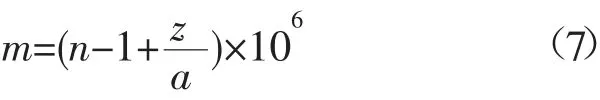
式中：a为地球半径，m。

在海洋大气最底层——海气边界层中，由于海水的蒸发会出现一个大气修正折射指数梯度锐减的层结，这一层结称之为蒸发波导。由于大气修正折射指数的骤然变化，式（5）中的m不再是一个常数，电磁波传播会受到严重影响。特别是在蒸发波导层内，电磁波会被陷获到这一层，贴海表面传播。蒸发波导可以用蒸发波导高度hd和大气修正折射指数m(z)来描述，如图1 所示。

大气修正折射指数廓线可以由Battaglia 模型[5]来计算：

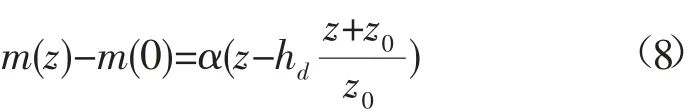
式中：z0为动力粗糙长度，通常z0=1.4×10-5，m；α是一个依赖于海面条件的参数，标准条件下α=0.120。为准确模拟蒸发波导环境下的电磁波传播，通常把式（8）代入式（1）来求解。

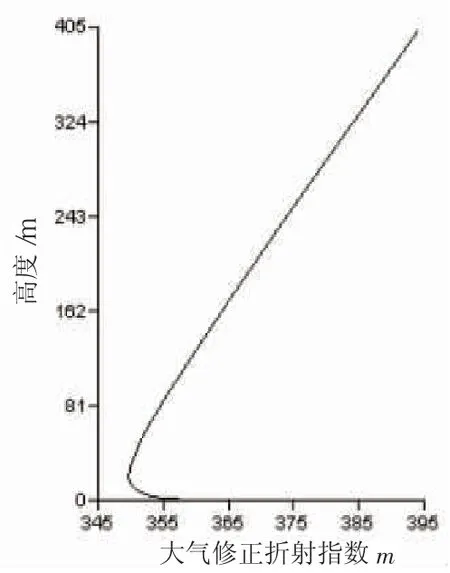
图1 20 m 高度蒸发波导的大气修正折射指数廓线

1.3 海面粗糙度的影响

在模拟电磁波的传播过程中[2，8]，通常采用完全平滑的海表面。然而在现实中，海表面并不是平坦的，为精确模拟粗糙海面对雷达探测性能的影响，电磁波在实际的海表面传播必须要考虑海面粗糙度。

以往的方法是用菲涅耳反射系数乘以一个粗糙度参数，该参数可由Ament[12]通过高度的高斯分布计算出来，并由米勒、布朗[13]用修正的正态分布来订正。

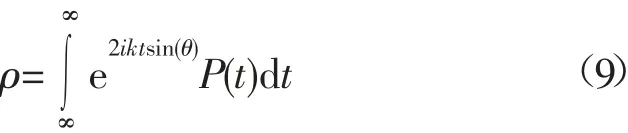
式中：P(t)是表面高度的概率密度函数。

粗糙度参数由米勒和布朗[13]计算给出：

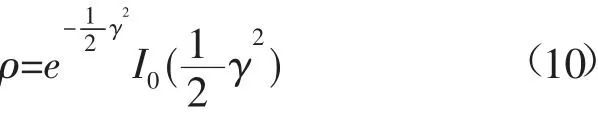
式中：I0是修正贝赛耳函数；γ=2khssin(θ)，其中hs=5.1×10-3V2w，Vw是风速和hs是波高的标准偏差。

上述方法没有考虑海面几何形状对电磁波传播的影响，基于这一原因，在Elfouhaily 海表面谱模型[6]和修正粗糙度参数基础上，采用了一种考虑风向对海面生成的方法[1]，来进一步研究海表面粗糙度的影响。

为了解风向对海表面几何形状生成的影响，将Elfouhaily 谱乘以角传播函数[6，14]，该角传播函数是电磁波传播方向和风向之间角度分量的量化[6，14]（图2）：

式中：φ 是电磁波传播方向与风向夹角；Δ(K)是由Elfouhaily 给出的一个函数[6]（图3）：

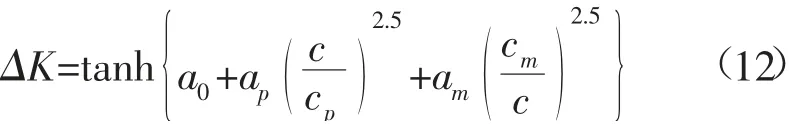
式中：a0=0.173，ap=4，cm=0.23 (m/s)；cp是在光谱峰值处的波相速度；am=0.13(u*/cm)；u*是摩擦速度。

利用角传播函数，可以将海表面谱作为k和φ的函数：

式中：SE(K)是Elfouhaily 海谱。图4 中描述了10 m/s 风速下不同φ 值的海谱。

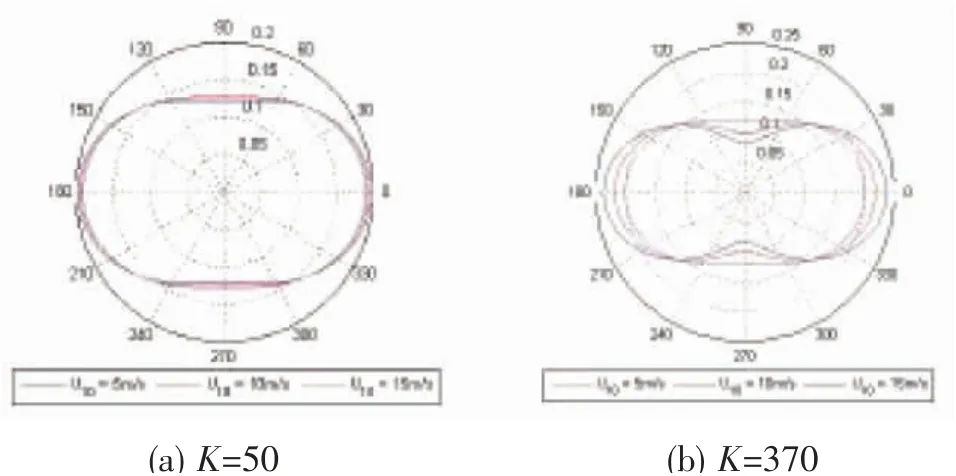
图2 角传播函数

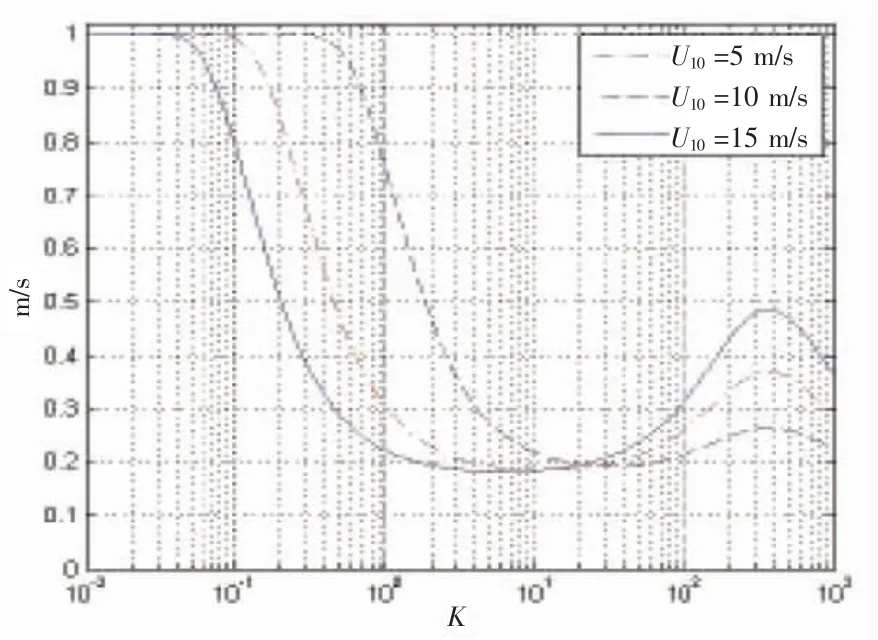
图3 不同风速下ΔK 函数的描述

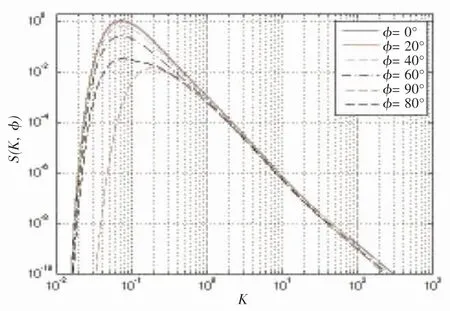
图4 10 m/s 风速下不同φ 值的Elfouhaily 海谱

2 蒸发波导环境下风速风向对电磁波传播的影响

2.1 风速对蒸发波导下的电磁波传播影响

在讨论风速对大气波导中电磁波传播影响时，根据粗糙海面的电磁散射理论[15]，风速越大，海面的粗糙度越大，而在粗糙度较大时也会产生数值结果不稳定现象。图5 给出风速分别在2 m/s，5 m/s，8 m/s，10 m/s，15 m/s，20 m/s 时，粗糙度条件下的电磁波传播损耗分布图。

根据海面粗糙度计算公式：

式中：U10为海面10 m 高度风速值，从而可以计算得出不同风速时的海面粗糙度，如表1 所示。

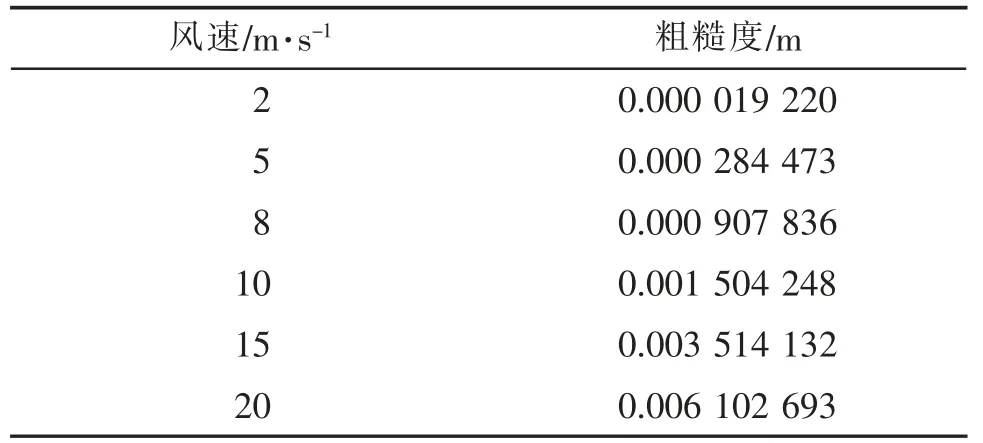
表1 不同风速时的海面粗糙度

图5 不同风速下电磁波传播损耗

从图5 可以看出，传播损耗随着传播距离的增大而不断增大，在同一传播距离处，由于海面粗糙度的影响，粗糙海面的传播损耗要比光滑海面大一些，因而风速越大，海面电磁波传播损耗越大。

2.2 风向对蒸发波导下的电磁波传播影响

为研究风向对电磁波传播的影响，利用电磁波传播模型，结合风速风向对海面几何形状的生成方法，数值模拟了架设10 m 高度，X 波段（9 GHz）发射源，在蒸发波导高度40 m，风速10 m/s，不同风向条件下的路径传播损耗。如图6 所示。

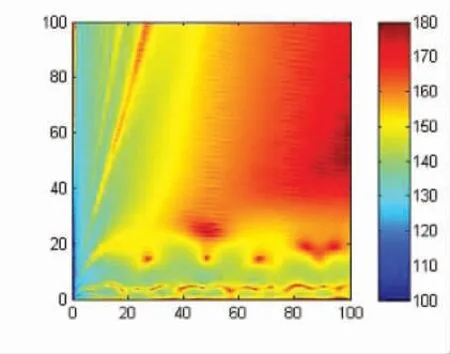
图6 电磁波传播路径损耗

图6 表示的是把海面作为光滑表面下的电磁波传播路径损耗，与图7 有明显差别。图7 是考虑了海面粗糙度对电磁波传播的影响，并数值模拟了电磁波传播方向与风向夹角分别为0°、45°和90°条件下的电磁波传播路径损耗。从图中可以看出，图7（c）在蒸发波导下方的电磁波传播路径损耗明显小于图7（a），这种差异是由于风向造成的，当电磁波传播方向与风向夹为0°时，其传播路径损耗远远大于在45°或90°条件下。

图7 不同电磁波传播方向与风向夹角φ 下的电磁波传播路径损耗

3 结论

为准确评估雷达系统的探测性能，需精细化模拟雷达电磁波在海洋大气中的传播。本文将蒸发波导条件下的大气修正折射指数廓线模型引入电磁波传播的抛物线方程中，进行裂步傅里叶（SSFA）算法求解；基于Elfouhaily 海表面谱模型和修正粗糙度参数，采用考虑风向对海面生成的方法，深入刻画海表面粗糙度对电磁波传播的影响。通过数值模拟蒸发波导环境不同风速风向下的雷达电磁波传播路径损耗，得到如下结论：

（1）风速会影响到海面粗糙度的大小，进而影响雷达电磁波的传播，在同一传播距离处，风速越大，海面粗糙度越大，海面电磁波传播损耗就越大。

（2）基于风向对海面几何形状生成的影响，分别模拟了电磁波传播方向与风向夹角为0°、45°和90°条件下的路径传播损耗，得到当电磁波传播方向与风向夹角为0°时，其传播路径损耗远远大于在45°或90°条件下，即顺风条件下电磁波传播损耗大于侧风。