微型桩加固土质边坡的加速度响应及其频谱特性研究
武志信,吴红刚,赖天文,牌立芳,王 飞
(1. 兰州交通大学 土木工程学院, 甘肃 兰州 730070;2. 中铁西北科学研究院有限公司, 甘肃 兰州 730030;3. 中国中铁滑坡工程实验室, 甘肃 兰州 730030;4. 西部环境岩土及场地修复技术工程实验室, 甘肃 兰州 730030)
微型桩是指桩径在 70~300 mm、长径比较大(一般大于30)的钻孔灌注桩[1],由于具有施工方便、快捷、见效快等优点,被广泛地应用于铁路等行业的边坡加固中。当滑面较浅、滑坡推力较小时,一般多采用微型桩加固支挡。微型桩是一种柔性构造物,在滑坡推力的作用下多呈现出弯曲变形,具有较好的延性,在地震作用下为了有效的减少脆性破坏发生的可能性,微型桩常被优先采用。在微型桩加固边坡研究中,主要讨论的是竖向承载作用下的微型桩结构[2-3],而对水平向作用下的微型桩结构研究较少,且学者多采用数值模拟的方法,而开展试验研究的较少。目前,国内外在微型桩的静力学研究方面已取得丰硕成果,冯君等[4]、周德培等[5]按照桩-土相互作用原理,讨论了具有顶梁固定微型桩组合结构的加固机制,并采用了弹性地基梁理论进行计算;王树丰等[6]、闫金凯等[7],通过现场大型模型试验,研究了黄土滑坡中微型桩桩群的滑坡推力及桩后土体抗力分布规律,滑坡推力在微型桩上呈三角形分布,滑面处推力达到最大值,桩后土体抗力与滑坡推力变化规律相一致;孙书伟等[8]、Holloway等[9]以及Brown等[10]指出,由于岩土体与桩的相互作用,微型桩群在水平受荷下会产生群桩效应;Sun等[11]、朱本珍等[12]基于梁柱理论和弹塑性p-y曲线法,建立了微型桩组合结构加固土质边坡的设计方法;孙厚超[13]对微型组合桩结构抗滑机理及其设计理论进行了研究;辛建平等[14]、胡毅夫等[15]进行了大型模型试验,分别研究了土质边坡中微型抗滑桩的破坏机制及微型抗滑桩组合结构前后桩的弯矩分布规律。在动力学研究方面,杨静[16]、李楠等[17]分别采用FLAC和土质边坡大型振动台试验对微型桩及其加固边坡的动力学响应特征进行分析,讨论了有桩和无桩情况下边坡的动力学特征;郑静等[18]通过大型振动台试验对微型桩平行体系和“人”字形体系的抗变形能力和承载能力进行了分析。
通过上述研究发现,目前国内外专家对于微型桩静力学方面进行了比较深入的研究,但对其动力学方面虽开展了岩质或土质边坡相关的动力响应与地震波频谱特性方面的研究[19-20],但这些研究成果并没有涉及到加固结构。鉴于此,为更加细致的研究加固结构和边坡的地震响应及其频谱特征,本文引入小波包变换这一数学工具[21],利用其可以对高频信息的信号能够进行更好的时频局部化分析的优点[22],分别对微型桩及桩间土体在不同频带下的加速度响应情况进行了分析,旨在为微型桩加固铁路边坡的动力合理性设计提供科学依据。
1 振动台试验设计
1.1 试验相似比及材料的选取、配置
本次振动台模型试验,以几何尺寸为基本参量(CL=10),根据相似原理,可推得其他相似参数为
( 1 )
由于密度ρp=ρM,加速度ap=aM,因此Fp/FM=103。
( 2 )
( 3 )
式中:ρ为密度;σ为应力;E为弹性模量;下标p、M分别为原量和模型量。
又考虑到动力相似的问题,由于试验过程土体产生较大的残余变形,弹性力几乎不存在,所以只考虑重力相似,由此可得
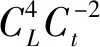
( 4 )
由式( 4 )可推出
( 5 )
模型其余参数可以根据量纲推得,见表1。
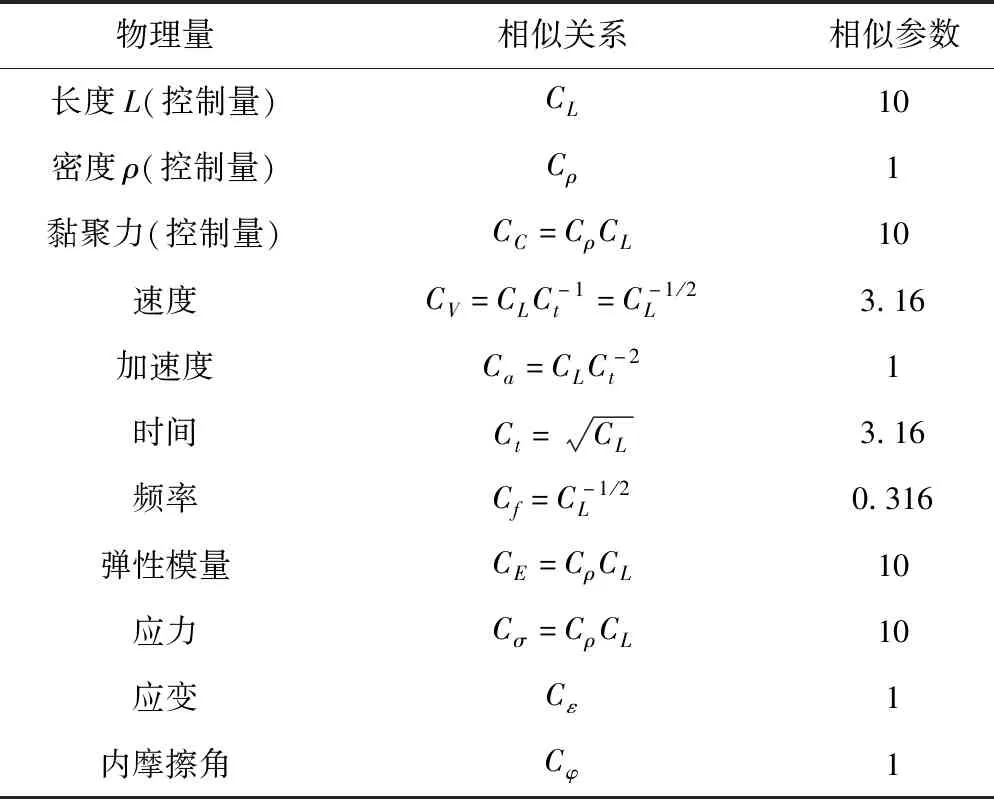
表1 模型设计相似参数
经计算,土体黏聚力、弹性模量和应力相似比产生的“奇异”较大,在模型试验中要使得模型材料完全满足相似比尺的计算要求很困难。但是考虑到本次试验主要研究目的是地震作用下微型桩支挡结构的加速度响应,并不是边坡本身,故这些相似材料的次要参数可以忽略。
1.2 试验模型设计与制作
本试验在甘肃省地震局兰州地震研究所的大型地震模拟振动台上进行。该振动台可输入规则波和不规则波,有效频率范围为0.10~50 Hz,最大承载力为25 t,最大加速度1.7g,振动台台面尺寸为4 m×6 m。
模型箱的内槽尺寸为3.0 m×1.5 m×1.14 m,采用了刚性密封模型槽,模型长边采用2 cm厚透明玻璃钢,可便于观察模型变化,且在玻璃钢表层衬了一层聚乙烯塑料以减少模型与箱体之间的接触摩擦。模型箱用2 cm厚钢板外加等边角钢焊接作为其主体框架,用2 mm厚型钢板在模型箱水平振动方向上进行围护,振动边界上的减震层采用4~5 cm厚的聚苯乙烯泡沫。滑带采用一层特氟纶塑料布进行模拟,试验中以重塑黄土为主要材料,通过控制重塑土的密度、含水量控制材料黏聚力、内摩擦角等参数,以满足材料物理性能相似的条件,通过试验确定的滑体和滑床的物理力学参数见表2。试验中微型桩采用内径1.5 cm的薄壁钢管,壁厚0.2 cm,内充填砂质黏土,长70 cm。连系梁采用4 cm×4 cm的松木条模拟,微型桩和连系梁之间采用钻孔连接,并用AB胶固定,制作完成的试验模型见图1。

表2 试验材料物理力学参数

1.3 测试断面及元件布置
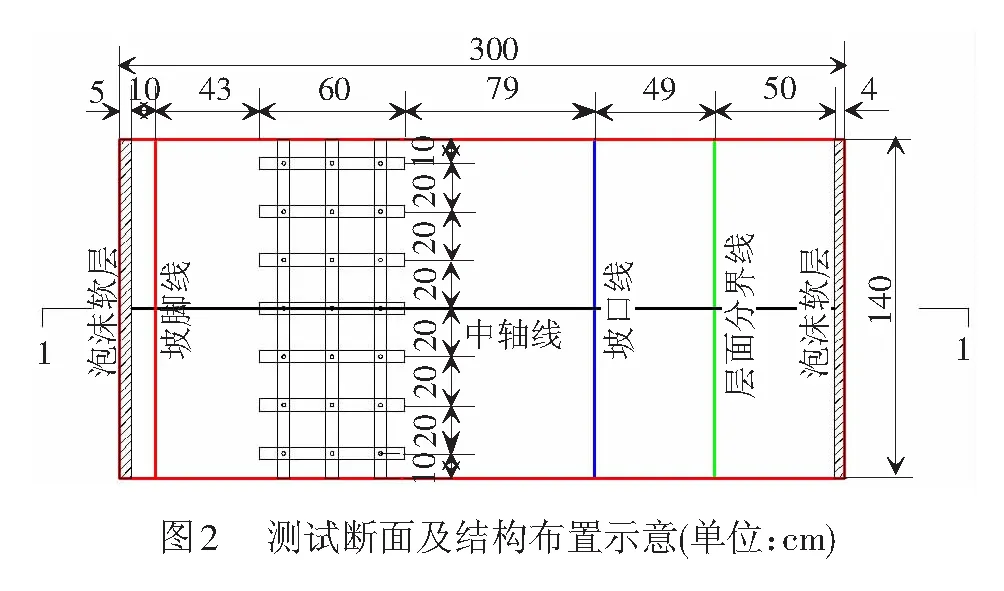
考虑到模型箱边界效应的影响,将本次试验所用到的加速度传感器布置在主断面1-1的前后排微型桩及滑体中,其结构布置见图2,加速度传感器布置见图3,其中悬臂段35 cm,锚固段35 cm。

1.4 加载制度设计
在该振动台试验中采用正弦波及El-centro波进行不同方向、不同程度的加载,由于水平地震是诱发滑坡、导致支挡结构破坏的主要原因[17],因此本文主要研究El-centro波在水平向加载方式下的加速度响应,试验加载工况见表3。

表3 试验加载工况
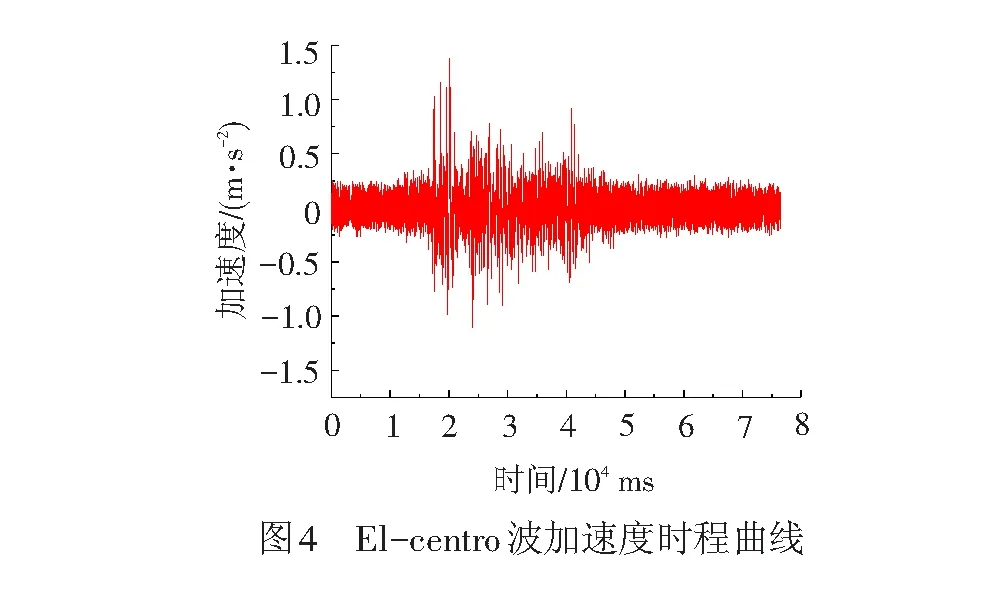
若地震波的时间压缩比不小于1∶3.16时,会造成地震波频谱成分过于复杂而产生失真的情况,从而导致对试验数据的采集及处理产生不良影响。因此,本试验中的地震波并未按照相似比例进行压缩,在试验过程中输入了El-centro波的原形波[23]。El-centro波加速度时程曲线见图4,试验前输入白噪声测试模型初始动力特性。
2 地震波的小波包变换
小波变换是一种时间-尺度分析方法,在时间、尺度(频率)两域都具有表征信号局部特征的能力,具有多分辨率分析的特点。小波包变换是基于小波变换的进一步发展,能够提供比小波变换更高的分辨率,解决了分析信号低频部分时间分辨率差而高频部分频率分辨率差的问题[24]。
2.1 小波包分解层数的确定
由小波包分解原理可知,对地震波采取小波包分解时可以进行无限层次的的分解,但是在实际的分解过程中,分解层数过低或者过高都不利于地震波的分析。当分解层数过低时,地震波信息的提取效果达不到理想的程度;而当分解层数过高时,可能会出现假频现象,不能保证较高的分辨率,而且随着分解层数的增大其运算量也增大,会产生处理速度慢的后果。因此,通常采用下以式确定小波包的分解层数[25]
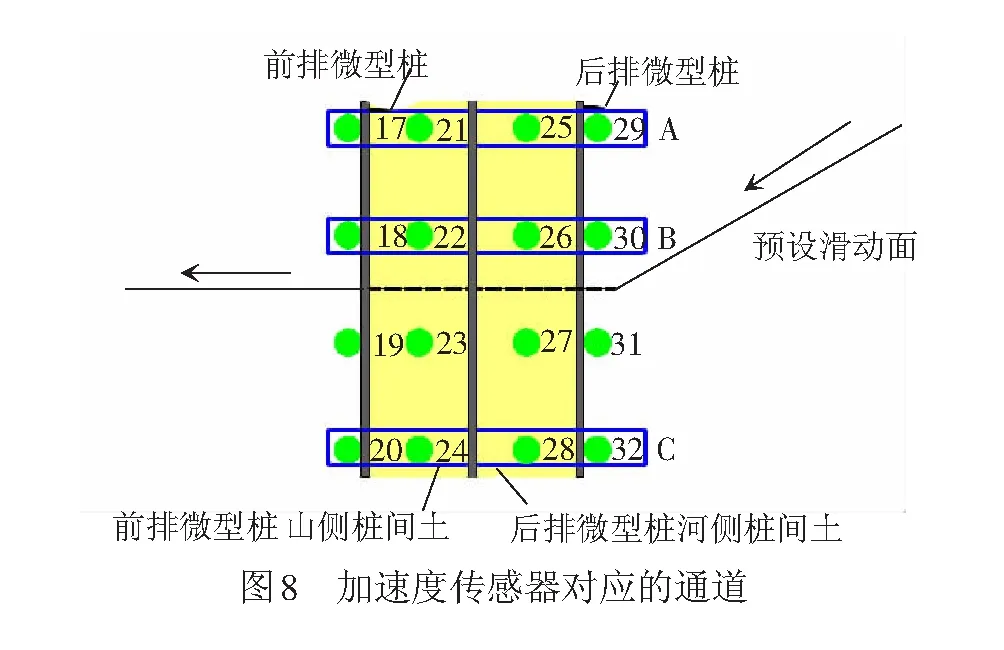
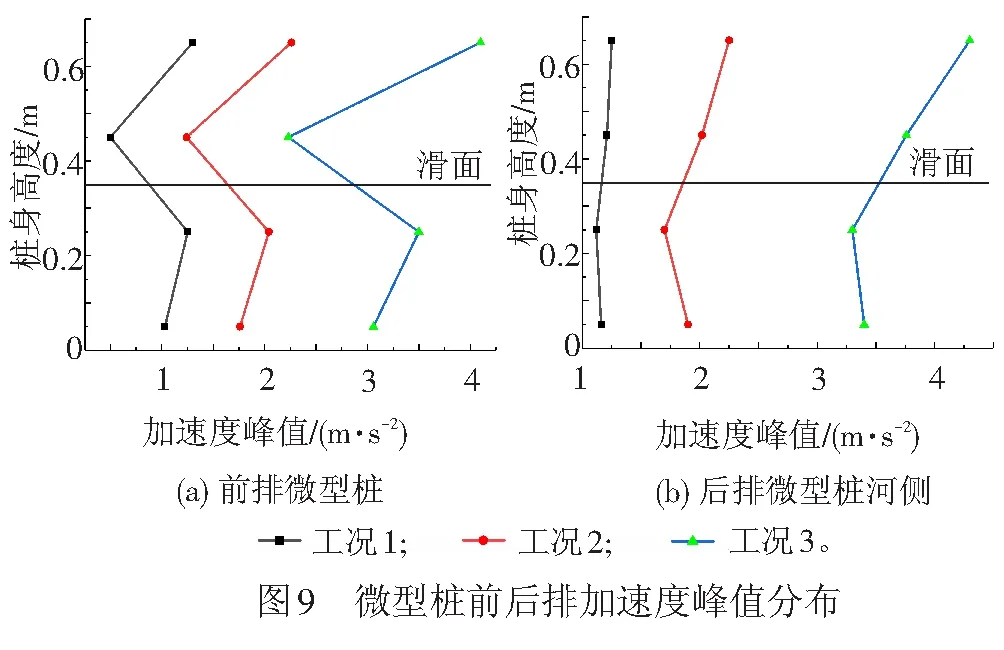
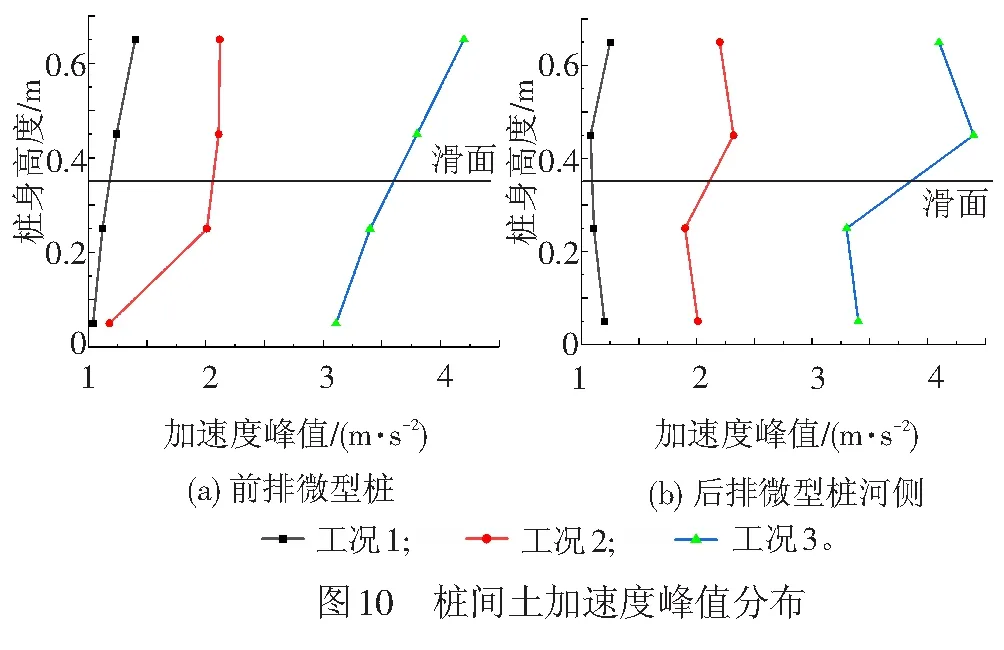
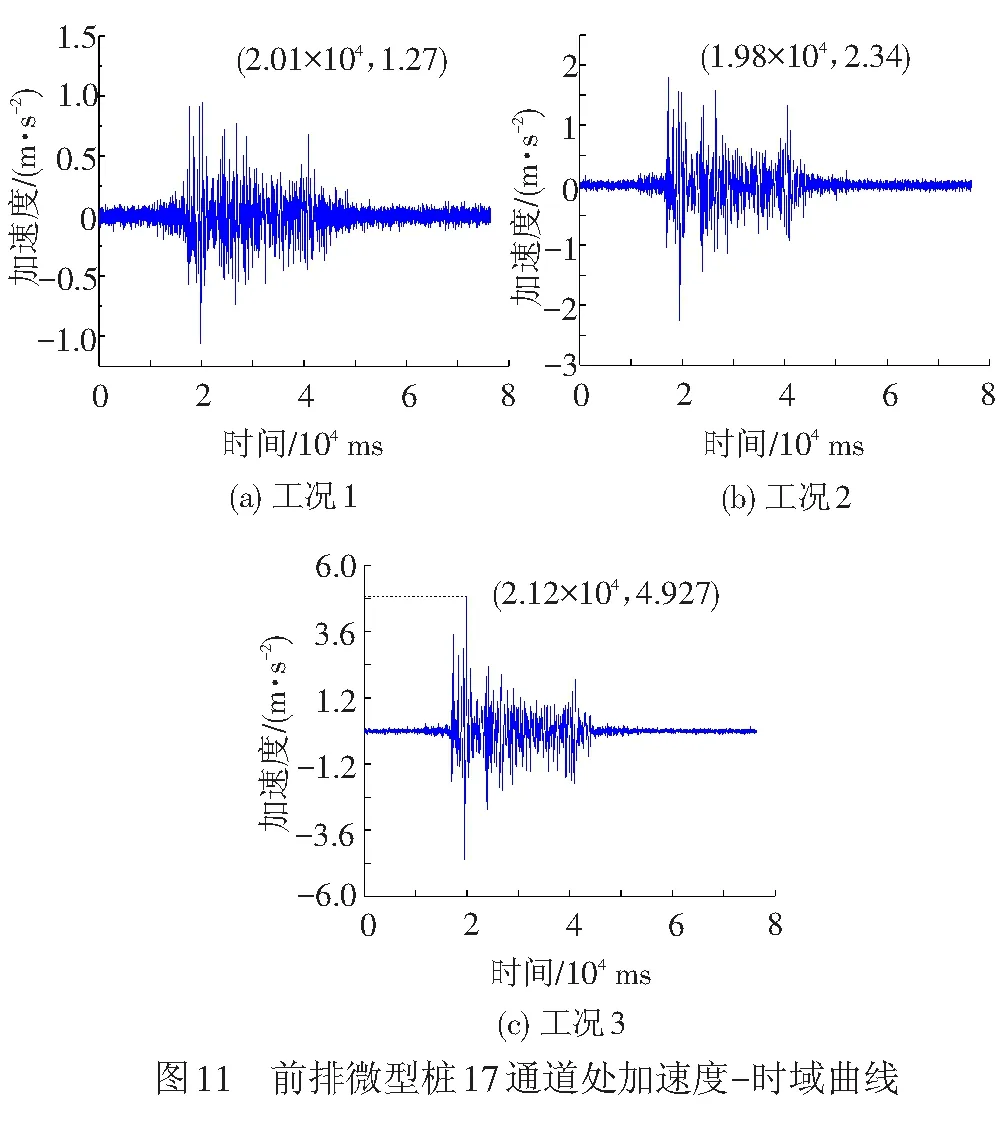
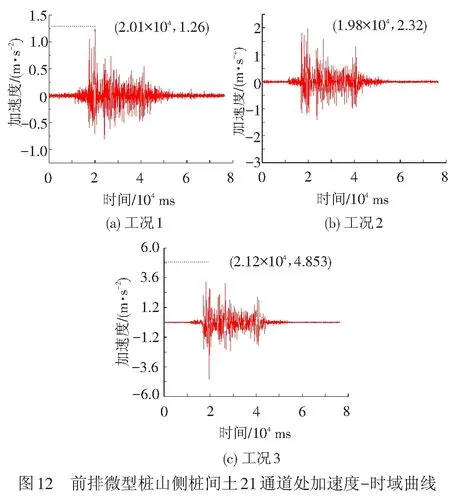
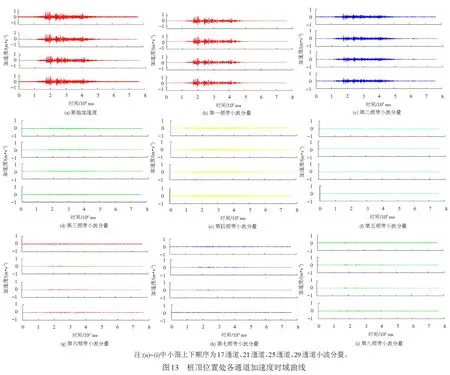
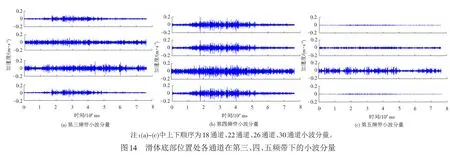
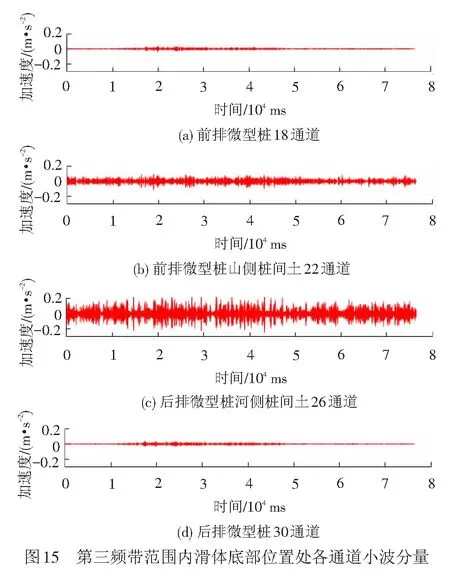
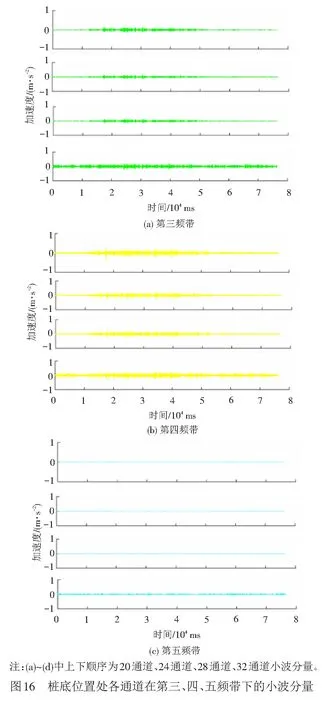
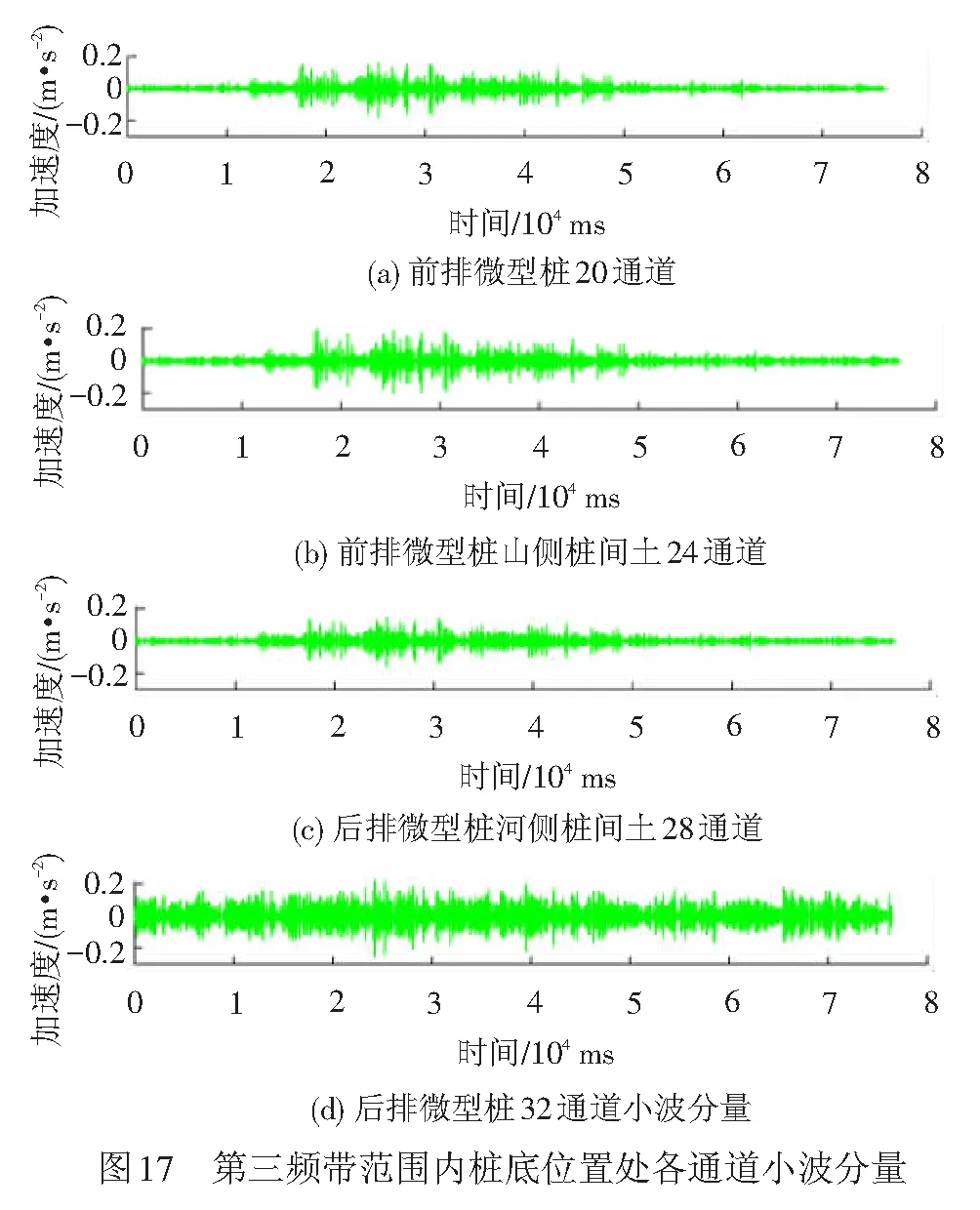
0 ( 6 ) 式中:k为地震波分解的层数;Ls为地震波信号的长度。 在该试验中,地震波信号的采样时间间隔为0.01 s,则其采样频率为100 Hz,地震动信号的持续时间一般为10~20 s,故该信号长度Ls约为29~210。将Ls代入式( 6 )可得,小波包的分解层数介于0~9层之间,综合考虑分辨率及频带宽度,本文认为当分解层数为3时,可以满足分析要求。 由1.2节可知,本次振动台试验输入地震波的有效频率范围为0.10~50 Hz,依据Shannon采样定理[26]可得,其Nyquist频率为50 Hz,进行3层分解后,共有23=8个小波包,则每个频带的宽度为50/8=6.25 Hz,对应的最低频带为0.10~6.26 Hz,各频带对应的频率范围见表4。 表4 各频带对应的频率范围 小波分析中应用的小波函数是多种多样的,选取各不相同的小波函数对信号处理的效果也会有所不同[27]。小波函数中的Daubechies(简称db小波)函数具有良好的近似对称性、光滑性及紧支撑性,在地震等非稳态信号的分析中具有明显的优势[28],该小波函数按系数N的不同又可以划分为db1—db10小波基。在目前的应用中,使用最多的是db3、db5、db8,本文中选取db8作为本次振动台试验的小波基函数。 工况1作用下,坡顶位置处出现了两条长度约为15 cm的竖向裂缝,分析其原因是由于水平向地震作用对坡体的张拉破坏而形成的,见图5(a);在模型坡肩位置出现了两条斜向裂缝,裂缝呈弧形,表面有贯通趋势,这两条斜向裂缝出现的原因是由于在水平地震波的作用下,坡体沿着水平方向来回振动,坡肩位置处的土体出现了震陷现象,且裂缝两侧的土体产生不均匀沉降而引起的,见图5(b)。 工况2作用下,坡顶后缘出现了两条长度为140 cm的纵向贯通裂缝,见图6(a),分析其原因是由于在坡顶后缘滑动面位置处张拉作用而产生的。同时,在坡体后缘滑面埋设位置处坡体也发生了张拉变形,并伴随有斜向裂缝的出现,见图6(b)。 在本次试验中,一直加载地震波直至坡体出现整体失稳后研究微型桩的变形情况,由GB 50011—2010《建筑抗震设计规范》[29]可得,工况3所对应的设防烈度为9度,在该地震波作用下,坡顶位置出现了深浅不等的多条裂缝,裂缝多呈圆弧型,部分裂缝已延伸至滑床,长度约为15~72 cm,分析其原因是由于水平向地震波的张拉作用而形成的,见图7(a)。同时,在工况3作用下,坡面整体发生了坡面流,见图7(b),且滑体较原来位置滑动了22 cm左右,见图7(c)。由此说明坡体已发生了塑性破坏。 通过上述分析发现,当试验加载的工况较小时,如在加载工况1和工况2地震波作用下坡体虽然出现了一些裂缝,但对于整个坡体,这些裂缝较细,且坡体未见明显位移或土体坍塌现象,表明微型桩在这两个工况的地震波作用下对坡体的变形起到了很好地抑制作用。当加载到工况3后,坡体已整体失稳,但在这个过程中微型桩群桩身并未发生断裂破坏,只是出现了一定程度的倾斜,见图7(d)。可以表明:微型桩桩间距布置合理,且其在地震作用下加固土质边坡起到了很好的作用。 本次试验对3种工况下微型桩及桩间土的加速度峰值的分布规律进行了研究,并通过小波包工具主要对工况1下微型桩及桩间土的加速度频谱特性进行了深入分析,研究了两者的加速度值在不同频段内的变化规律。其中,加速度传感器在前后排微型桩桩身及桩间土中所对应的通道见图8,约定微型桩面向坡脚一侧为河侧,面向坡体一侧为山侧。图8中,A、B、C分别表示桩顶位置、滑体底部位置及桩底锚固端位置处所对应的传感器通道。 计算工况1—工况3下的微型桩前后排加速度峰值及桩间土加速度峰值,加速度分布图见图9、图10。 由图9(a)可见,在振动作用下,前排微型桩在桩顶及滑面以下处,加速度放大效应明显,但加速度峰值在桩底位置存在缩小现象;由图9(b)可见,后排微型桩的加速度峰值近似呈斜线分布,在桩顶位置处加速度峰值达到最大。 从图10(a)可见,前排微型桩山侧的桩间土加速度峰值近似呈直线分布,沿桩身高度加速度峰值不断增大,在桩顶位置处加速度峰值达到最大值,在滑面以下存在缩减现象;由图10(b)可见,后顶位置处加速度放大效应明显。 通过比较图9、图10可知,除后排微型桩河侧的桩间土外,微型桩及桩间土的加速度峰值往往在桩顶处达到最大值,造成该现象的原因是由于加速度沿边坡高程的放大效应所造成的,这与杨长卫等[30]的研究结果相吻合。为了更好地反映地震波作用下水平向加载时加速度的动力响应情况,此处选择前排微型桩及该桩山侧桩间土在桩顶位置处(即17和21通道)的加速度-时域曲线进行分析,见图11、图12。 由图11可知,工况1、工况2、工况3在El-centro 波作用下,加速度峰值分别为1.27、2.34、4.927 m/s2,其加速度峰值增幅分别为前者的1.84倍、2.11倍,随着输入的El-centro波动峰值加速度的增大,测点加速度响应效应越显著。 由图12可知,工况1、工况2、工况3在 El-centro 波作用下,加速度峰值分别为1.26、2.32、4.853 m/s2,其加速度峰值增幅分别为前者的1.84倍、2.09倍,随着输入的El-centro波动峰值加速度的增大,测点加速度响应效应也越显著。 上述研究方法只是针对加速度峰值进行了分析,对于不同频段地震波的激励下,边坡中微型桩及桩间土加速度的响应情况并不能表达出来,而通过小波包工具可以对这方面的问题进行深入研究,下面通过小波包分解对不同工况下两者的加速度频谱特性进行研究。 以工况1的El-centro 波进行小波包分解为例,由于其他位置的小波包分解图形跟桩顶位置的小波包分解图相类似,为节省篇幅,不再一一列出,在此选取前排微型桩、前排微型桩山侧桩间土、后排微型桩河侧桩间土以及后排微型桩在桩顶位置处分别对应的17、21、25、29(见图8中A)通道为例进行分析,桩顶位置处各通道加速度时域曲线见图13。 本文将12.51 Hz以下的地震波均视为低频波,由图13可见,对微型桩和桩间土加速度影响的主要频段为低频段,即第一频带(0.10~6.26 Hz)和第二频带(6.26~12.51 Hz),故在实际工程设计与施工中,应采取减振、隔振措施以避免微型桩的自振周期与低频地震波的振动周期相重合,产生共振现象[31]。从整体分析,微型桩桩身及桩间土体的加速度值在第一频带内均为-1~1 m/s2、在第二频带内均为-0.4~0.4 m/s2,在其他相同频带内两者的加速度值范围也大致相同。结合图13,对比微型桩及桩间土在滑面附近及桩底锚固端的各个通道处的小波包分量图(篇幅原因,本文未列出图形)可得,影响微型桩及桩间土加速度的地震波主要为低频波,表明边坡对低频地震波有放大效应,对高频部分有滤波作用[32]。但是在滑面附近与桩底锚固段位置处,高频地震波对桩间土与桩身加速度的响应也比较强烈,其具体分析见4.3节。 为了研究高频地震波作用下,滑面附近位置处微型桩与桩间土加速度值的异同,在此选取滑体底部位置处分别对应的18、22、26及30通道(见图8中B)在三、四、五频带下的小波分量图为例来进行分析,滑体底部位置小波分量见图14。 由图14可知,在三、四、五高频带地震波作用下,滑体底部位置处桩间土的加速度响应比微型桩的更加强烈。为了对该处微型桩及桩间土的加速度值进行更深层次的研究,在此选取上述4个通道在第三频带下的加速度-时域图为例,滑体底部位置处各通道小波分量见图15。 由图15可知,滑体底部位置处桩间土在22、26通道处的加速度分别为-0.08~0.08 m/s2、-0.2~0.2 m/s2,而前后两排微型桩上的18、30通道的加速度值相差不大,均在-0.04~0.04 m/s2范围内波动,说明第三频带内该处桩间土的加速度值要明显大于微型桩的加速度值,分析其原因是由于微型桩作为一种柔性结构,能够有效地将能量传递给土体,从而使其自身所受到的地震作用较小。同时发现,后排微型桩河侧的加速度值明显要比前排微型桩山侧的加速度值大,分析其原因是由于后排微型桩河侧的桩间土更靠近坡体,在振动过程中,坡体后部首先开始变形,出现沿滑面下滑的迹象,从而造成该处加速度响应更加强烈的现象。由于其他各高频带在该位置处均存在类似的情况,此处不再详细论述。 为了研究高频地震波作用下,桩底锚固端位置处微型桩与桩间土加速度值的异同,在此分别选取20、24、28、32(见图8中C)通道在第三、四、五频带下的小波分量为例,桩底位置处各通道小波分量见图16。 由图16可以看出,在第三、四、五高频带地震波作用下,桩底位置处后排微型桩(32通道)的加速度响应明显要比该位置处其他通道的更加强烈。为了对该处微型桩及桩间土的加速度值进行更深层次的研究,在此选取上述4个通道在第三频带下的加速度-时域为例进行分析,见图17,其他各高频带内的情况与第三频带相似,故此处不再细列。 由图17可知,桩底位置处前排微型桩(20通道)的加速度值为-0.18~0.18 m/s2;桩间土24、28通道处加速度值分别为-0.2~0.2 m/s2、-0.15~0.15 m/s2;而后排微型桩(32通道)的加速度为-0.24~0.24 m/s2,明显要比其他3个通道处的加速度值大。再对比桩间土的加速度可得,24通道处的加速度值要比28通道处的加速度值大33%左右。 综上可得,在高频地震波的作用下,桩底位置处后排微型桩的加速度响应最为强烈,分析其原因是由于坡体沿滑面下滑,后排微型桩受力较大且其变形受到桩底良好的锚固性能限制所造成的。 通过本次振动台试验,对微型桩及桩间土的加速度峰值分布规律进行了分析,并利用小波包工具对水平向加载的El-centro波进行了分解,且对各频段地震波作用下加速度的频谱特性进行了研究,结论如下: (1) 由于加速度沿高程放大效应的影响,微型桩及桩间土的加速度峰值往往在桩顶处达到最大值。 (2) 影响微型桩和桩间土加速度的主要频段为低频地震波,即第一频带(0.10~6.26 Hz)及第二频带(6.26~12.51 Hz)。 (3) 高频地震波作用下,滑体底部位置处桩间土的响应情况较微型桩更加强烈,而在桩底位置处后排微型桩的加速度响应更加强烈。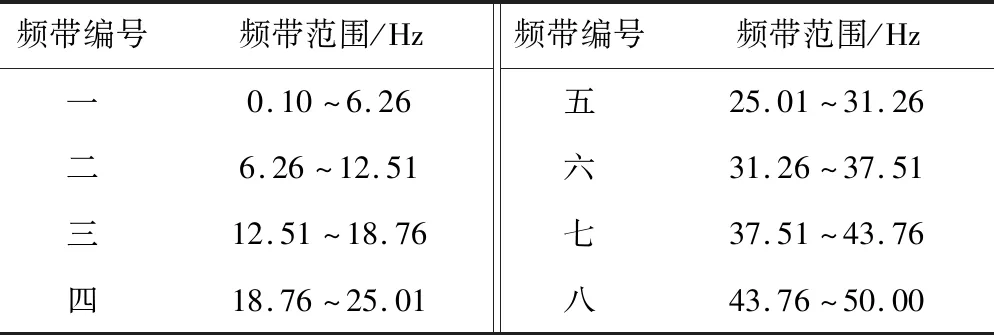
2.2 小波包基函数的选择
3 试验现象分析



4 试验结果分析
4.1 加速度峰值及其时域响应分析
4.2 桩身与桩间土加速度的频谱对比分析
4.3 滑面附近位置桩身与桩间土加速度的频谱对比分析
4.4 锚固端处桩身与桩间土加速度影响的频谱对比分析
5 结论

