以问题驱动学习方式变革 促核心素养提升
江苏省扬中市永胜中心小学 陈 敏
随着社会的发展,全球教学改革进入素养时代,基于适应社会发展的核心素养教育已成为教育者的共识。近年中国首创并提出了数学学科核心素养,其导向旨在通过学校教学时空的重新分配,重新组织教育要素,引导学生穿越数学学科壁垒,关联知识与生活,彰显学习的实践性与创造性,过与以往不同的学校生活。在实践中我们发现基于问题驱动的学习是打通知识到素养的高效通道。
问题驱动是一种建立在建构主义理论基础上的学习方式,学生在设问、释问和反思的过程中萌生自主学习的动机和欲望,理解知识的本质内涵,构建知识网络。就像布鲁纳所说:“教学过程是一种提出问题和解决问题的持续不断的活动,思维永远是从问题开始的。”在课堂上我们应该引领学生经历这样的过程:围绕某一主题,设计问题情境,学生在问题驱动下开展任务活动,进而解决问题,获得学习成果。在这一过程中获得的具体知识即为数学学科观念,情感内化即为必备品格,其解决问题的思路和方法即为关键能力,从而最终提升学生的数学核心素养。(如图1)
在具体操作层面,基于问题驱动的教学过程可如图2 所示。在整个过程中教师需要创设情境、搭建支架、支持合作和组织引导,学生则需要经历发现问题—分析问题—设计方案—实施方案—得出结论并交流评价。
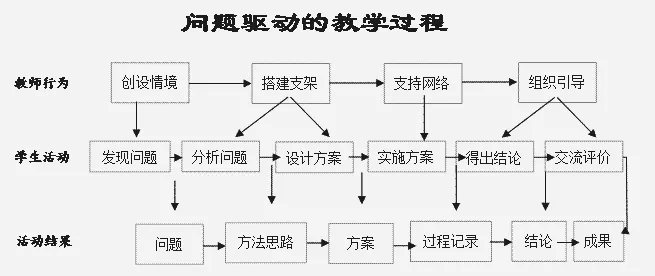
图1
一、用“现实性问题”创设情境
设计具有学科意义的真实的问题情境是学生问题解决的基础,学生研究的问题需是“可触的”也是“可感的”。所谓“可触的”是指问题的高度应在学生的最近发展区内,精准把握问题跨度,个人或者是团队跳一跳能够得到;所谓“可感的”则是指贴近学生的生活实际或者学科知识经验实际,在解决问题的过程中,学生能够利用已有的经验作为起点来研究新问题。

图2
以《百分数的认识》一课为例,苏教版教材是从比较三场比赛的投篮情况(如图2)入手,引导学生计算出每场比赛投中次数是投篮次数的几分之几,继而通分比较。在这一环节的处理上,我们常常会看到两种不同的提出问题的方式:方案A:1.出示表格中投中次数一栏(将投篮次数遮起来),问:仅仅比较投中次数行吗?生:不行,因为不知道一共投了多少次。2.出示表格中投篮次数一栏(将投中次数遮起来),问:仅仅比较投篮次数行吗?答:不行,因为投中的次数不知道。3.出示完整的表格,问:那么应该比什么?生:比较投中次数是投篮次数的几分之几。方案B:直接出示例题表格,问:怎样比较这三场比赛的投篮情况更合适呢?小组内讨论交流。我亲身试验过两种方案,结果发现方案B 更能激起学生交流的欲望,更能听到学生真实的声音。方案A 具有强烈的暗示性,学生一般都“聪明地”知道单独比较一组数据肯定是不可取的,六年级的问题不会那么简单。有了这样的心理暗示,做深入思考的学生也就少了。而在方案B 的交流中,学生没有前期的铺垫和挟制,思维也更原始地展示在大家面前,学生在交流和碰撞中反而将问题解释得更加清楚。
二、用“连续性问题”搭建支架
“连续性”问题也就是“问题连续体”,它能引导学生产生连续性学习,搭建支架,将数学学习引向深入,这是一节课解决问题的关键所在。这种学习方式也有人称为“问题化学习”,需要从系统的高度透视问题与问题之间的关系,把握每一个问题的诸要素及相互关系,关注这个问题在全局中的位置,也包括从更广阔的视野全面多视角地透视某个问题系统,把握问题之间的联系,并在问题系统的相互联系中理解问题、分析问题、解决问题并反思问题。

图3
根据问题间的关系不同,可以设计不同类型的“问题连续体”。
(一)线性问题连续体
这一类型采用顺向加工的方式,从简单问题入手,由浅入深、逐步递进。数学学科知识具有较强的连贯性(见图3),学生在掌握一个知识点以后才能进入下一个知识点的学习。在这种类型中教师的问题设置是关键,突出层层驱动,目的是让学生体验“数学知识的发生发展过程”,实现小步骤达到教学目标。整个教学过程由“问题链”驱动学生思维逐步深入。
还以《百分数的认识》例题的教学为例,学生通分比较出三场比赛的投篮情况后,教师出示第四场比赛,第一问:如果此时比较四场比赛的投篮情况该怎么办呢?第二问:这个分数也可以转化成分母是100 的分数来比较吗?第三问:分母统一为100 后有什么好处?这里连续三问即引导学生经历了百分数产生和发展的过程。第一问学生可能会转化成小数,或者用更大的数作为公分母来通分比较,但是这样比较麻烦。第二问引导学生体会到分数可以转化为分母是100 的分数。第三问通过比较,学生感受到统一公分母为100 的好处在于统计和比较的方便。这三问有层次地渐近地向目标问题趋近,有效地解决了授课中的重点。
(二)树形问题连续体
采用目标→手段的分析方式,往往根据教学目标先审视要解决的问题,在达成目标的过程中分解为若干个子问题,驱动学生思维,以量变引起质变,引导学生掌握知识、获得方法。
百分数意义的提炼和概括一直是本课教学的难点,教师在引导学生理解了例题中百分数的意义都表示投中次数是投篮次数的百分之几以后,将对于百分数意义的理解放置到不同的情境中进行。学生广泛交流搜集到的百分数的意义,发现百分数在不同的情境中表示的意义不同,但是都有一个相同点,都表示一个量是另一个量的百分之几。这样并列展开,因势利导,逐个解决,让几个子问题的解决同时驱动后续问题的解决。
不管是线性问题连续体还是树形问题连续体,各问题间并不是孤立存在的,它们是一个有机的整体,相互关联,相互作用。这些连续体能为学生提供思维的支架,帮助有效解决课堂重点难点问题。
三、用“结构性问题”支持网络
如果说“连续性问题”可以让学生理清知识产生的脉络,弄清问题的前因后果,那么“结构性问题”的优势则是理清各数学知识间的内在联系,找到连接点、嫁接点、整合点,从而建构知识网络。在问题网络中,不仅各个问题系统或局域之间建立起复杂的系统联系,而且各个系统内的具体问题与其他系统内的问题也将建立起错综复杂的联系。
理解百分数的意义需要学生理清分数和百分数之间的关系,明晰它们的相同点和不同点。在联系实例理解百分数的意义后,教师引导学生练习,并追问:分母是100 的分数都可以改写成百分数吗?现在你认为分数和百分数之间有什么关系?通过具体的实例,学生明晰了:虽然百分数可以看作分母是一百的分数,但只能表示两个量之间的倍数关系。掌握了分数和百分数的连接点,将百分数的认识纳入了他原有的知识框架中去,这才算是完成了对于百分数意义的进一步理解。
四、用“反思性问题”组织引导
知识点是数学的外显形式,而数学思想方法则是数学的内在形式,是学生获取知识,发展数学能力的动力工具。对于数学思想方法的提炼主要依靠学生对于学习过程的反思和总结。 在反思中学生把已经解决的问题作为反思的对象,进行适当的总结拓展,扩展思维的深度和广度。
在《百分数的认识》一课中,在学生对百分数的意义深入理解后教师及时引入十分数和千分数,并引导学生思考:不管是百分数、十分数还是千分数,它们有什么共同的地方?学生思考这些引申问题后体会到这些分数都统一了分数单位,使统计和比较更为方便。这也就深刻理解了百分数存在意义及其价值,也是内在数学思想方法的体现(见图4)。
反思型问题可以帮助学生自我计划、自我监控、自我调节。数学思维的发展主要是指由较低层次上升到更高的层次,但是只要学生没能对自己的活动进行反思,他就达不到高一级的层次。
数学教学的本质是问题教学,核心是问题构建。因此在数学教学中,利用“问题”这一抓手,让学生在“再创造”中获得一种自由生长的力量,让探究成为学生的一种自主学习行为,从而提升数学素养,经历不一样的精彩课堂生活。
- 青年心理的其它文章
- 建构主义视觉下的初中英语单元主题阅读教学设计

