基于物理知识约束的数据驱动式湍流模型修正及槽道湍流计算验证

张亦知，程诚，范钇彤，李高华，李伟鹏

上海交通大学 航空航天学院，上海 200240

湍流边界层广泛存在于航空、航天、建筑、生物等领域，其主要的计算方法包括直接数值模拟(DNS)、大涡模拟(LES)和雷诺平均Navier-Stokes(RANS)模拟。直接数值模拟求解非定常流动中的湍流扰动，大涡模拟湍流小尺度结构而分辨湍流大尺度结构，具有较好的预测精度，但DNS和LES所需的计算网格规模与雷诺数的指数幂成正比，在高雷诺数下的计算成本巨大，使得利用DNS或LES开展高雷诺数流动仿真存在困难[1]。RANS通过引入湍流模型方程模化所有的时空多尺度湍流脉动，通过显式表达式[2]或偏微分方程[3]求得雷诺应力，其计算量与雷诺数呈弱相关关系，计算效率高，在工程中得到广泛应用。

然而，RANS的预测精度与DNS或LES存在差异，且在实际应用中湍流模型的选择依赖于设计者的经验,通过调整或优化湍流模型中的个别系数难以提高其预测精度，且不具有普适性。RANS计算最大的不确定性来源于湍流模型方程的固有形式[4-5]，近年来，利用数据挖掘和机器学习方法修正RANS湍流模型显示出巨大的潜力和前景[6-7]。

Duraisamy等[8-9]利用流场反演获得湍流模型修正项，进而使用神经网络建立流场特征与修正项之间的映射关系，获得嵌入式的湍流模型，经重构后湍流模型计算结果更接近实验数据。Ling和Templeton[10]利用DNS和LES的计算结果，发展了机器学习修正的RANS湍流模型，比较了不同机器学习方法，如支持向量机、决策树以及随机森林对流场不确定性的预测效果，结果表明这些方法在与训练样本相异的流场中均能准确地捕捉流动特征。Xiao等[11]使用贝叶斯方法量化RANS计算中模型形式的不确定性，并加入经验知识约束，结果表明该方法利用稀疏的先验数据能较好地捕获基准模型的误差，获得更准确的后验平均速度分布。Wang等[12]的研究结果表明，雷诺应力的预测能力是影响RANS计算精度的重要因素，由此建立了基于雷诺应力张量的随机森林机器学习重构方法，并针对湍流方管及典型分离流动进行了模型重构。Wu等[13]采用相似的方法构造了随机森林模型，给出了RANS计算置信度的先验估计。Zhang等[14]在翼型的近壁区、尾迹区等不同区域分别构造了径向基神经网络，模化了高雷诺数湍流边界层中的涡黏项，并将其实时地引入流场求解过程，提高了计算准确度，且在翼型或流动条件变化时具有一定通用性。在湍流计算领域，基于大数据的机器学习方法具有广阔的应用前景，文献[15]对数据驱动式湍流建模理论和方法进行了综述分析。

数据驱动式建模方法依赖于样本数据的个数和质量，小样本或样本冗余误差会导致模型的失真或失效。为克服数据驱动式建模对数据样本个数和质量的依赖关系，需要引入基于物理知识约束的先验条件，在建模过程中约束模型的边界和搜索空间，有利于避免非物理现象的产生，提高模型的预测精度。近年来，基于物理知识的数据驱动式建模成为研究热点，Raissi等[16]以自由振动的圆柱为研究对象，将有限的速度散点数据作为训练样本，利用神经网络重构的过程中，引入流体控制方程作为先验的物理知识约束，对流动参数进行了预测，获得准确的升/阻力预测结果。Raissi等[17]构造了基于物理信息的神经网络，用于求解非线性偏微分方程，利用少量的训练数据，成功捕捉了系统的非线性特征。针对湍流模拟的RANS方程，尚未发现基于物理知识约束的数据驱动式建模方法。

准确预测湍流摩擦阻力具有重要的工程价值，本文作者在利用DNS数据研究湍流摩擦阻力的分解中，发现湍流摩擦阻力的分解项在湍流边界层的内层具有统一的比拟关系[18]，与雷诺数大小无关，与可压缩性无关[19]，并在槽道和平板湍流边界层中得到了验证[18-20]，结果表明该比拟关系是一种物理的、普适的规律，是一种先验的物理知识。本文基于该物理知识开展了针对S-A湍流模型的数据驱动式建模及修正，在建模过程中引入物理知识约束，对比了有/无物理知识约束的修正对槽道湍流摩擦阻力预测精度的影响。

1 基于物理知识约束的数据驱动式建模方法

1.1 经典S-A湍流模型

为封闭雷诺平均的Navier-Stokes方程，Spalart和Allmaras[21]构造了一方程湍流模型方程，通过求解标量运输方程来计算湍流涡黏系数并获得雷诺应力，具体形式为

(1)

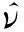
(2)

(3)

(4)

1.2 源于湍流摩擦阻力分解的物理知识

固壁与流体相对运动而产生摩擦，摩擦阻力可以表征为固壁对流体做功的一种形式，对于槽道湍流而言，摩擦阻力做功，一部分能量通过黏性直接耗散转换成热能，一部分能量则通过湍动能生成项维持湍流态。基于这一思想，Renard和Deck[23]推导了湍流摩擦阻力系数Cf的分解公式：

(5)

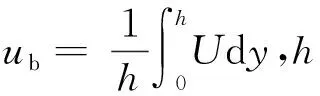
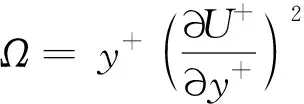
(6)

式中：a1=2.644；b1=1.895；c1=-0.805；a2=1.777；b2=1.118；c2=1.642。式(6)中仅有一个自变量y+，图1表明拟合结果与DNS数据的符合良好。本文将式(6)作为一种先验物理知识约束引入到数据驱动建模中。

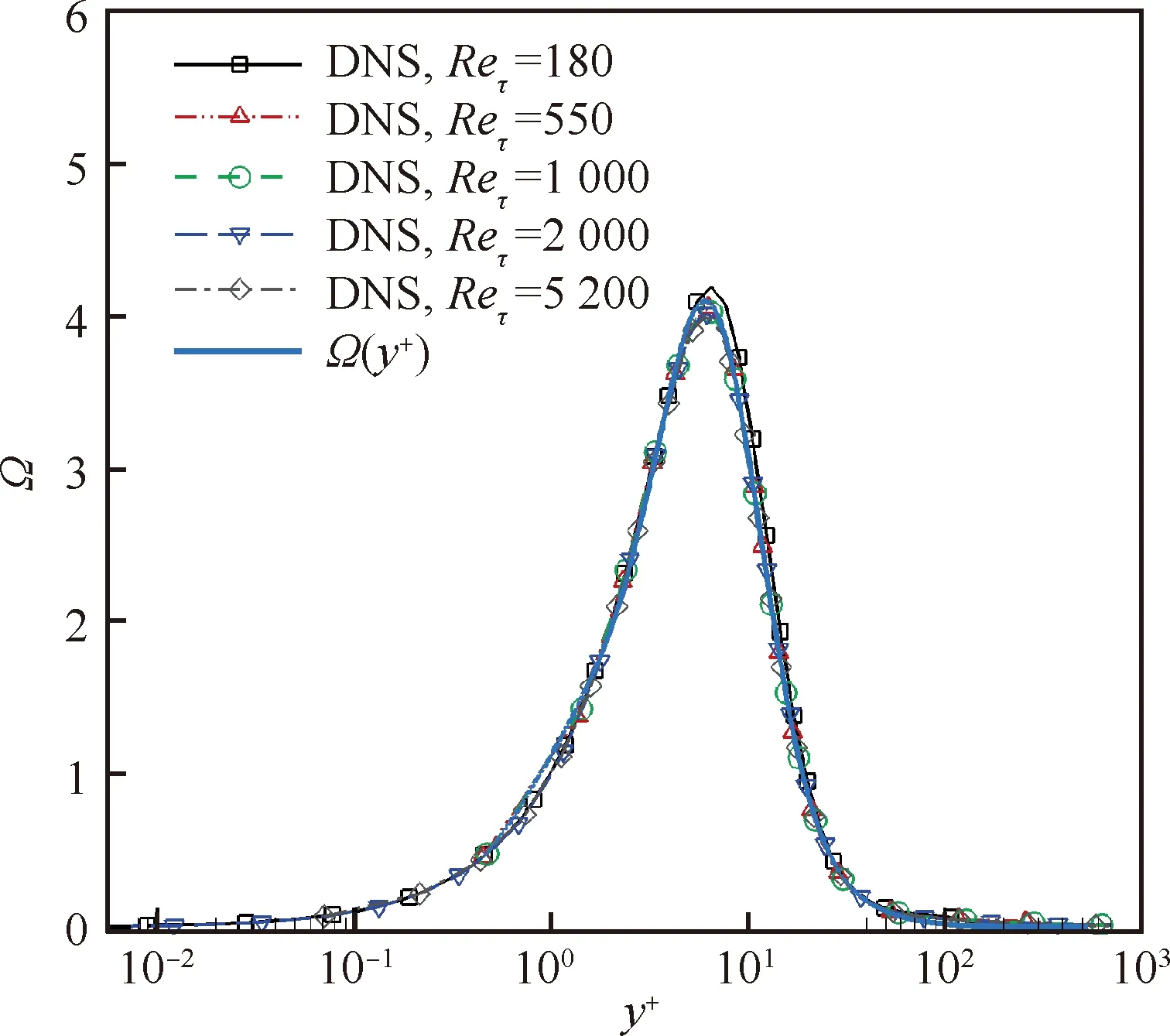
图1 不同雷诺数下直接黏性耗散项的法向分布Fig.1 Direct viscous dissipation curves along wall-normal direction under different Reynolds numbers

1.3 基于物理知识约束的湍流模型修正方法

保留S-A湍流模型方程的基本形式，对生成项P添加修正因子β，修正后的湍流模型方程为

(7)

修正因子β对流场的影响是全局性的，其取值随着法向高度的变化而变化。本文通过添加修正因子β来校正S-A湍流模型，其本质是在S-A湍流模型中添加了源项的校正量δ，即δ=(β-1)P，其大小与生成项相关。初始时β=1，校正量δ均为0，式(7)即退化为原始的S-A方程。通过引入修正因子β，拟使得S-A湍流模型预测更准确，即校正后的S-A湍流模型计算结果更接近于真实解，真实解可取高精度的DNS、LES结果，也可利用试验测量的数据进行标定，本文中的真实解为DNS计算结果[24]。

为获得准确可靠的修正因子，需要设定合理的目标函数，结合高效的优化方法，快速获得修正因子分布。传统方法对模型中系数进行调整优化，例如对冯卡门常数(κ)或湍流普朗特数(σ)的校正[24-25]，但其难以克服重要流场物理特性(如雷诺数)的影响。由此，考虑到湍流摩擦阻力的预测与平均流向速度剖面紧密相关，且引入式(6)作为物理知识约束，设定目标函数为

(8)

式中：(Uj-Uj,DNS)2表征对平均流向速度剖面的逼近程度；(Ωj-Ω(y+))2表征对近壁黏性耗散项分布的逼近程度；Nc为网格单元数。值得指出的是，修正因子β与直接黏性耗散和平均流向速度之间不存在直接的量化关系，仅存在隐式关联与映射。

为对比分析有/无物理知识约束对湍流摩擦阻力的预测误差，本文也采用了基于平均流向速度的目标函数：

(9)

由于设计变量个数与网格数量相当，使用有限差分法求解梯度计算量巨大。伴随方法(Adjoint Method)是一种高效的梯度求解方法，其计算规模与设计变量的数目基本无关，可大幅减小梯度的求解时间。伴随方法以偏微分方程系统控制理论为基础，Jameson[26]首次将伴随方法应用于气动设计中，把气动设计转换为一个满足特定约束的最优控制问题，梯度求解的计算量约为2倍的流场计算量。伴随方法包括连续伴随和离散伴随，本文采用离散伴随方法[27]，伴随方程和梯度的表达式为

(10)

(11)

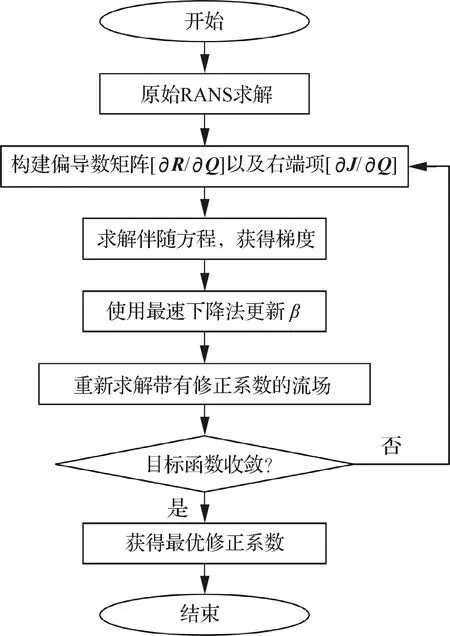
图2 湍流模型修正优化流程Fig.2 Optimization process of turbulence model correction

以二维方程[29]来验证伴随方法所求得的梯度与有限差分法的一致性，图3对比了有限差分法与伴随方法所得的梯度分布，其偏差小于0.57%，属于合理范围内。

图3 伴随方法中的梯度验证Fig.3 Gradient verification in adjoint method

2 计算结果与分析

图4 直接黏性耗散项的法向分布Fig.4 Distribution of direct viscous dissipation in wall-normal direction

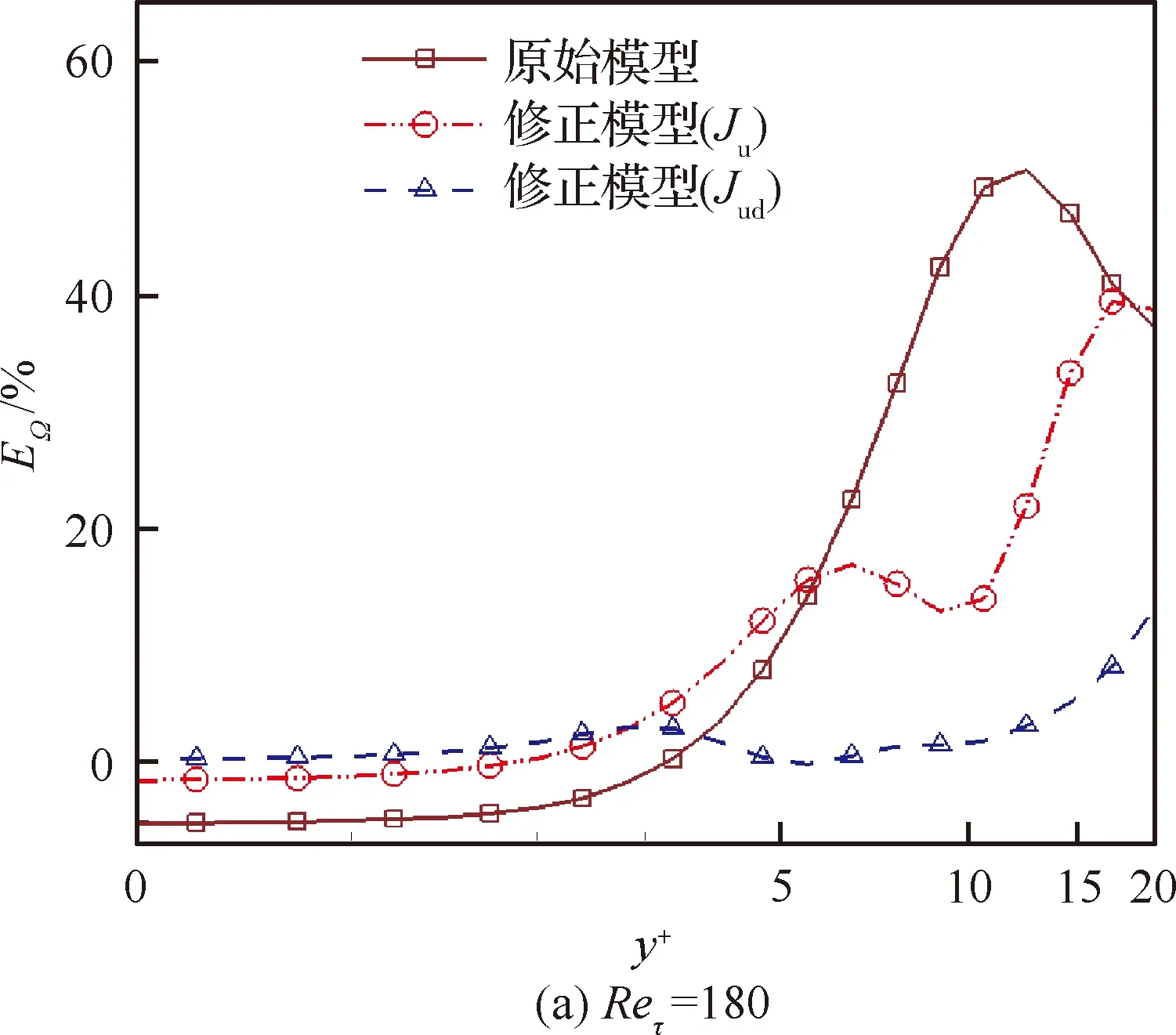
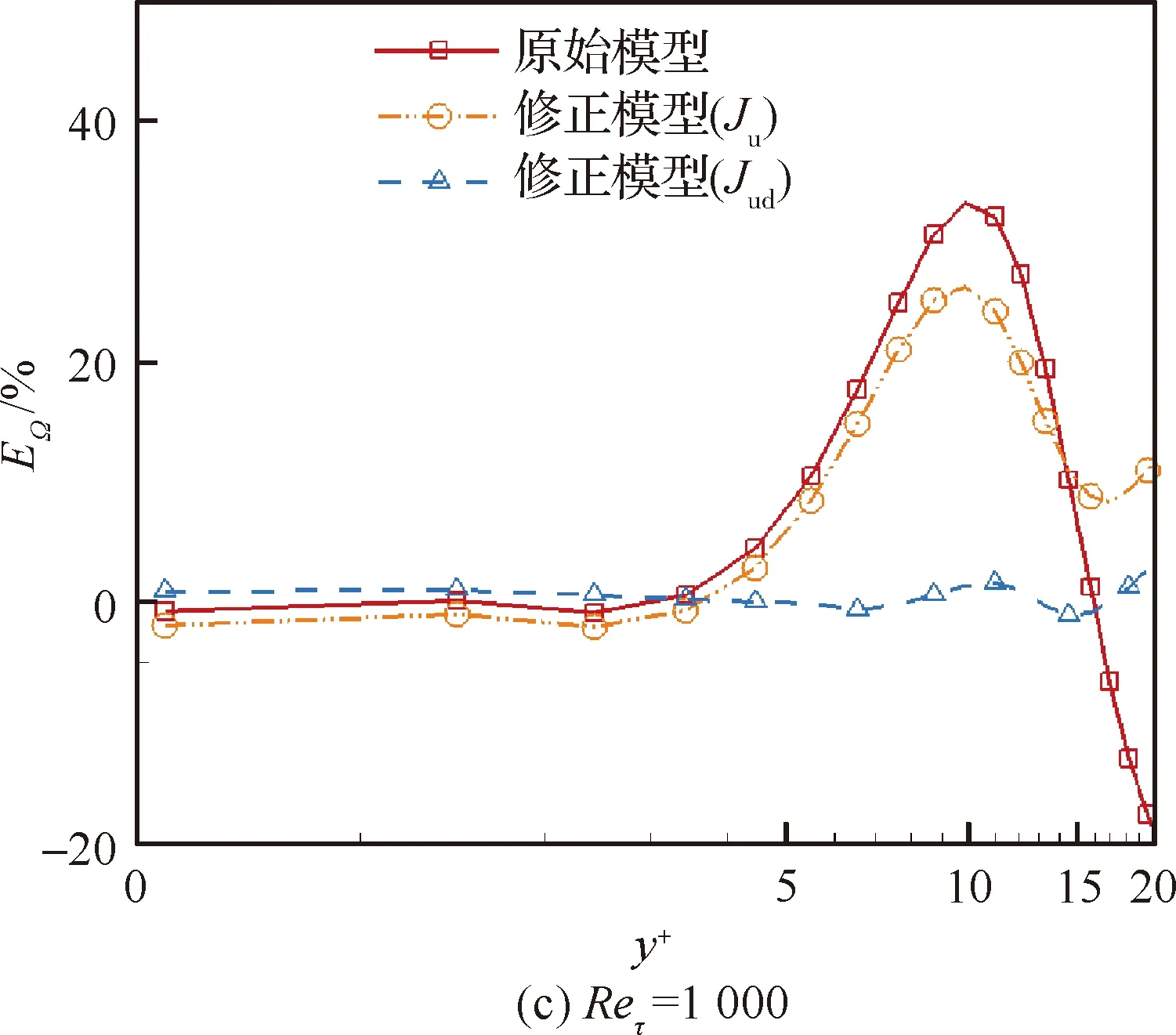
图5 直接黏性耗散项相对误差的法向分布Fig.5 Distribution of relative error of direct viscous dissipation in wall-normal direction

图4和图5中的比较结果表明，原始S-A湍流模型对近壁区直接黏性耗散项的预测存在明显偏差；如果通过数据驱动模型仅修正流向速度剖面，对直接黏性耗散项的预测有所改善，但误差仍然较大；在数据驱动建模的目标函数中，进一步引入关于直接黏性耗散的先验物理知识作为约束条件，预测精度显著改善，计算结果与真实结果的相对误差小于3%。

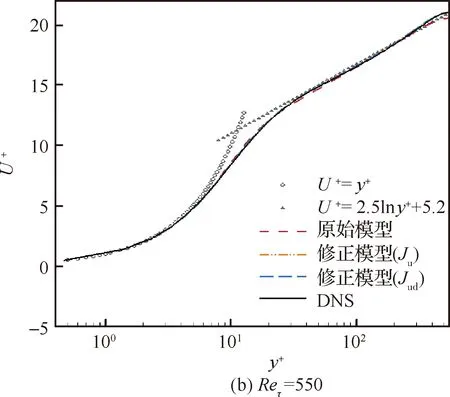
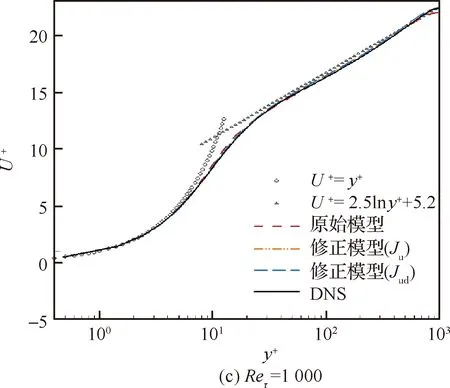
图6 平均流向速度的法向分布Fig.6 Distribution of averaged streamwise velocity in wall-normal direction

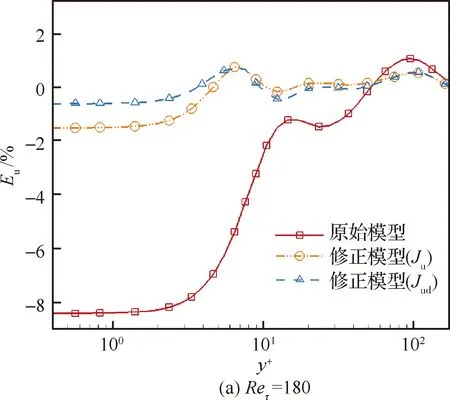
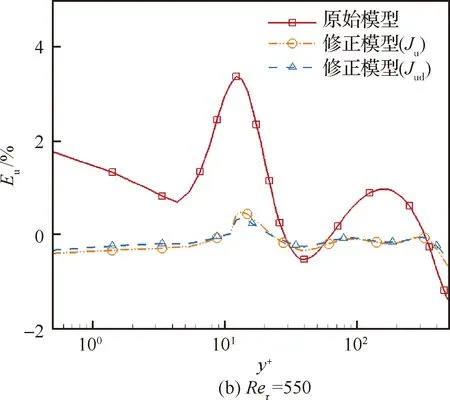
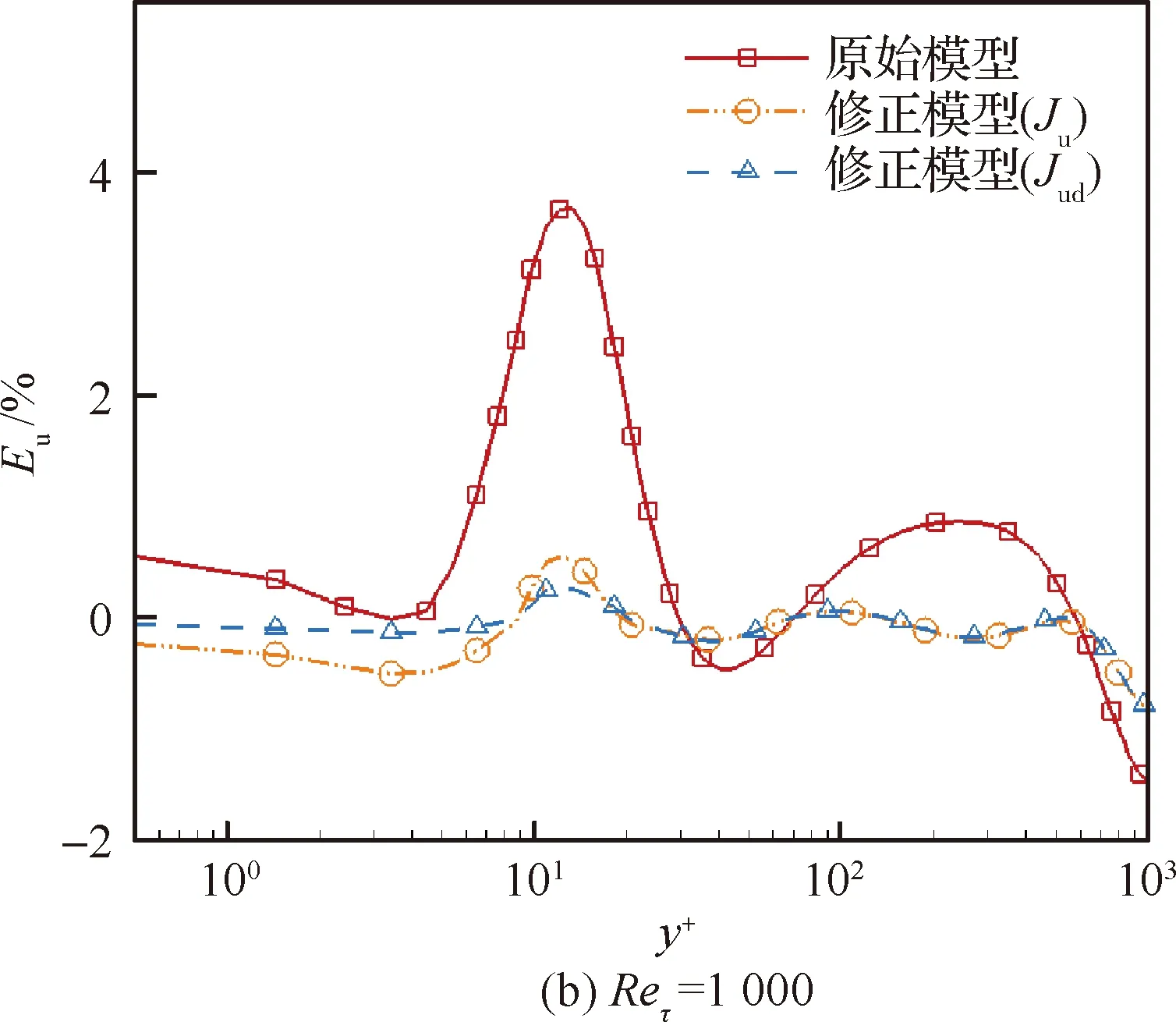
图7 平均流向速度相对误差的法向分布Fig.7 Distribution of relative error of averaged streamwise velocity in wall-normal direction

图8比较了不同雷诺数下修正因子β的变化情况，注意原始S-A湍流模型中修正因子恒为1。当采用Ju为目标函数时，仅根据流向平均速度进行模型修正，修正因子β的法向变化趋势基本与图7中流向平均速度误差的分布一致，说明修正因子β具有较好的活性，可根据当地的平均速度误差对S-A模型中的湍流黏性生成项进行相应调整。当采用Jud为目标函数时，引入了直接黏性耗散项作为流向平均速度修正的补充，以Reτ=180的槽道为例，对于复合目标函数修正因子β做出相应的调整，在y+=4.65处达到峰值，说明目标函数Jud起到了复合校正效果。同时，图8中β系数随流场位置及当地流场变量的变化而发生演变，也说明了本文建立的伴随优化方法计算可以有效地建立对方程预测精度的调整和修正。需要注意的是，修正因子β的取值范围在-10～20之间，说明原始S-A湍流模型中的生成项存在低估或者逆传递现象。修正因子的本质作用是在S-A湍流模型中引入δ=(β-1)P作为源项的修正项，该修正项的取值范围根据预测结果与真实结果的偏差而定。

图8 修正因子β的法向分布Fig.8 Distribution of correction factor β in wall-normal direction

湍流摩擦阻力是一个较小的壁面变量，目前针对大型客机的总阻力预测，利用RANS计算要确保阻力误差在1 count以内仍是巨大的挑战，其中最为困难的是湍流摩擦阻力的准确预测，其约占总阻力的50%以上。本文针对槽道湍流这一简单基础构型进行了数据驱动的湍流模型修正，在低雷诺数下其预测精度显著提高，而在较高雷诺数条件下，表1中的数据显示无修正的湍流模型对摩擦阻力的预测误差已经小于0.48%，通过模型修正，这个误差得到了进一步的减小。该结果表明，基于数据驱动式的湍流模型修正具有较好的应用前景。

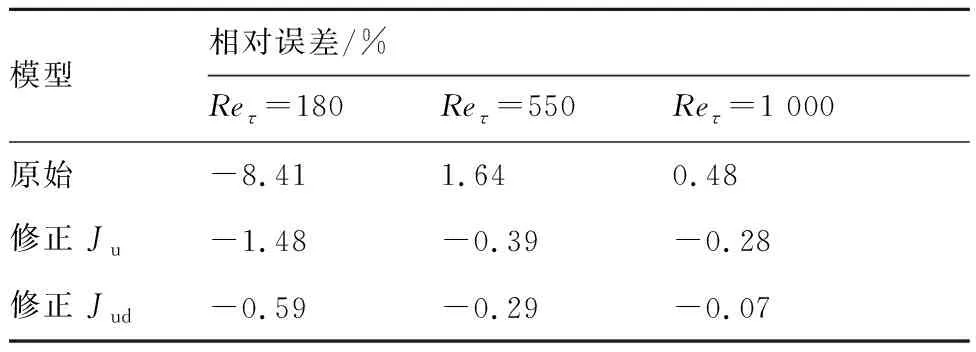
表1 壁面摩擦阻力系数的相对误差Table 1 Relative errors of skin friction coefficients

3 结论与展望

数据驱动式建模的本质是数据回归和优化问题引入物理知识的先验约束，一定程度上可降低对数据样本个数和质量的依赖，提高模型的预测精度。本文提出了一种基于物理知识的数据驱动式湍流模型修正方法，并以槽道湍流为研究对象验证了该方法的优越性，获得的结论包括：

1) 基于湍流摩擦阻力分解的先验物理知识，建立了一种基于物理知识约束的湍流模型修正方法，将物理知识显性地引入目标函数的设定中，结合伴随优化方法，高效率地获得修正因子的分布，以达到提高预测精度的目的。

2) 以槽道湍流为例，对比了有/无物理知识约束下的湍流模型预测精度，结果表明引入物理知识约束后，可提高对湍流摩擦阻力的预测精度。

本文研究存在如下不足，希望在后期研究中克服：

1) 引入的基于湍流摩擦阻力分解的先验物理知识，适用于无逆压梯度的湍流边界层，而对于有逆压梯度导致的流动分离问题，该物理知识的有效性需要进一步的验证，或引入更为普适的物理知识。

2) 仅开展了基于DNS数据的先验验证，而没有利用机器学习方法，如神经网络、决策树等，建立物理变量与目标函数之间的映射关系，以开展无数据条件下的后验验证。

3) 建立目标函数时，用到了DNS平均速度剖面数据，没有完全避免对DNS数据的依赖，在后期工作中有待进一步完善。