基于Hopfield神经网络的雷达多目标跟踪
王 伟, 史国友, 郑海涛, 王毓玮
(1.大连海事大学 航海学院, 辽宁 大连 116026;2.辽宁省航海安全保障重点实验室, 辽宁 大连 116026)
目标跟踪是运用各种观测和计算手段,实现主体对所关注运动客体的状态进行建模、估计、跟踪的过程。随着人工智能的不断发展,在今后的无人船应用当中,由雷达等传感器测得目标,然后根据其过去直到当前的观测值,预测和估计其运动轨迹,对目标进行跟踪检测,进而针对目标做下一步操作,保障无人船的安全。目标跟踪技术[1]主要包括:数据关联、状态估计融合和航迹管理,而数据关联属于目标跟踪技术中需要解决的首要问题。
在目标跟踪技术当中,数据关联的作用是基础,不正确的数据关联将直接导致跟踪精度降低甚至丢失目标,数据关联的难度体现在传感器存在漏检、虚警以及在测量值比较密集的情况下的关联。国内外学者信息融合技术的研究,比较常用的数据关联算法包括最近邻方法、概率数据关联、联合概率数据关联、多假设方法等以上方法的改进算法。[2]联合概率数据关联(Joint Probabilistic Data Association,JPDA)是公认的目标跟踪中最有效的数据关联算法,利用落在跟踪门限内的当前扫描周期中的点迹,计算点迹和相应航迹的关联概率。JPDA计算包含关联事件构造和关联概率计算两部分。但该算法计算量过大,导致其实时性较差,同时随着目标的增多,JPDA可行事件的数量将呈指数级增长,发生组合“爆炸”。因此,需要比以上数据关联更精确的技术来解决数据关联问题。神经网络具有强大的模式识别和数据拟合能力,以及具有良好的鲁棒性与容错性,局部的损害会使得人工神经网络的运行适度减弱,但不会造成灾难性的错误。因此,将神经网络用于目标跟踪研究中可克服跟踪精度和快速响应的矛盾及数据关联方法的组合“爆炸”等问题。[3-4]
1 联合概率数据关联算法
联合概率数据关联算法是利用落在跟踪门限内的当前扫描周期中的点迹,计算点迹和相应航迹的关联概率,利用关联概率对当前点迹求权值来修正航迹,权值就是跟踪中的点迹,来自于目标的概率。[5]联合概率数据关联算法包含关联事件的构造和关联概率的计算两部分,其实质就是由关联事件构造的确认矩阵拆分得到关联矩阵,计算量测j与目标的关联概率βjt(k)。[6]
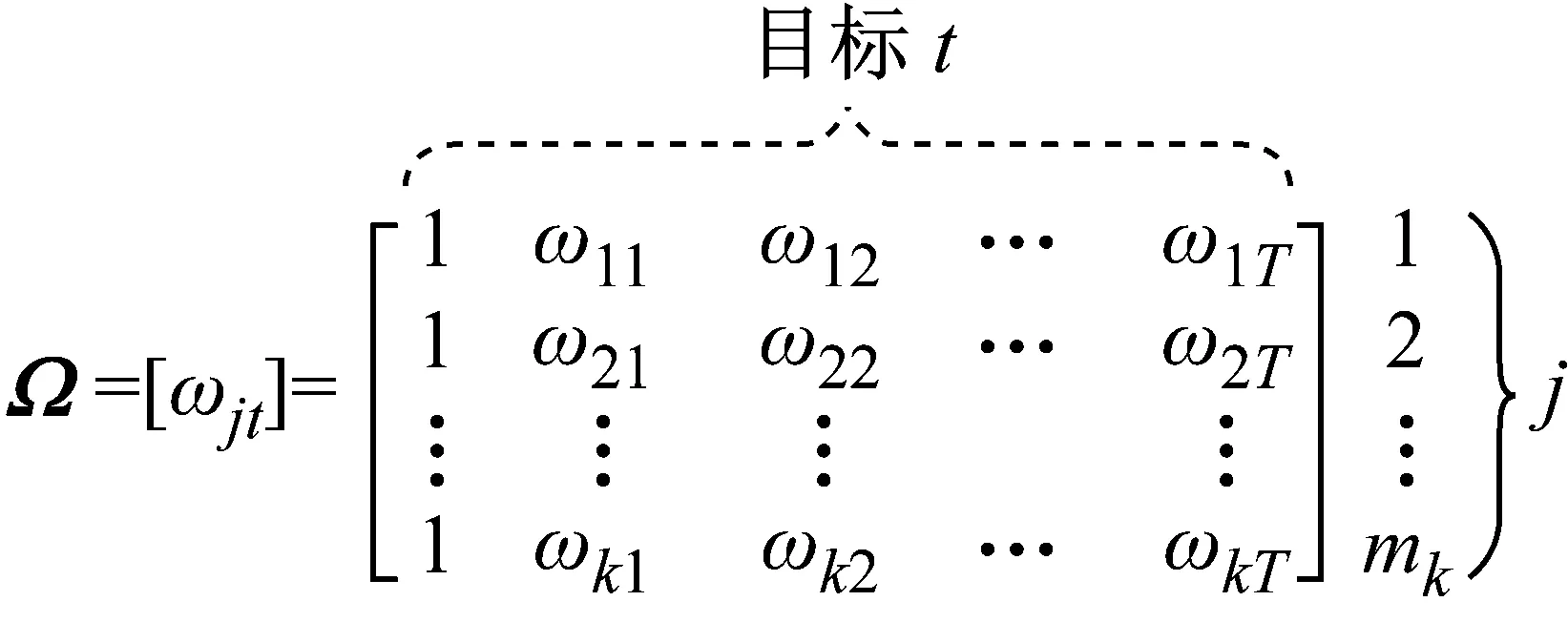
构造关联事件θi(k),为表示有效回波和各个跟踪门的复杂关系,引入确认矩阵Ω的概念,确认矩阵定义为
Ω=[ωjt],j=1,2,…,mk;t=0,1,…,T
(1)
式(1)中:ωjt为二进制变量,ωjt=1为量测j落入目标t的确认门内,ωjt=0为量测j没有落入目标t的确认门内,t=0表示没有目标。矩阵Ω的第一列元素ωj0全都是1,这是因为任一量测都可能源于杂波或者虚警。[7]
(2)
综上所述互联态势的确认矩阵为
j=1,2,…,mk;t=0,1,…,T
(3)
对于多目标跟踪问题,一旦给定反映有效回波与目标或杂波矩阵,则可通过拆分确认矩阵来得到所有的关联矩阵,对确认矩阵的拆分要遵循以下原则:在确认矩阵的每一行,仅选出一个作为互联矩阵在该行唯一非零元素,即满足可能事件的第一个假设是每个量测j有唯一的源。在互联矩阵中,除第一列以外,每列最多只能有一个非零元素。即满足可能事件的第二个假设是每个目标最多有一个量测j以其为源。[8]解释见图1。
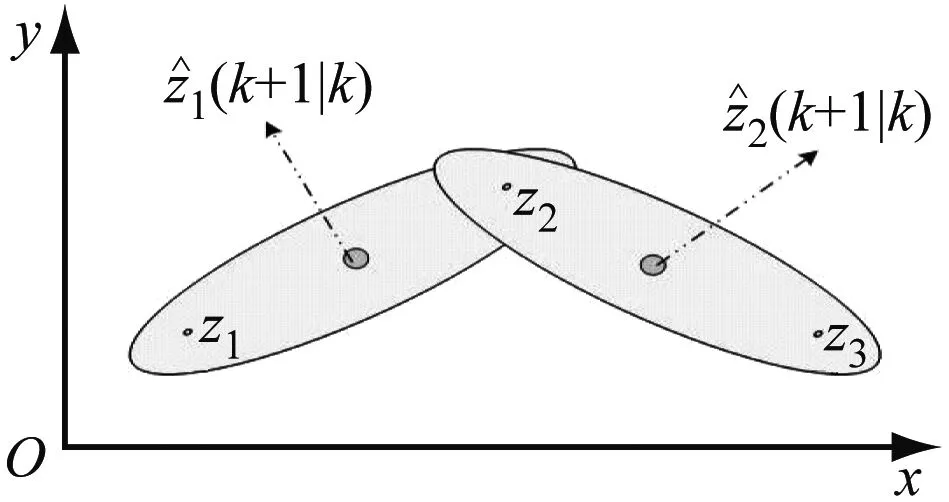
图1 两目标预测值及椭圆跟踪门观测值
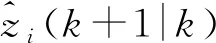

(4)
然后依据确认矩阵的两个拆分原则对上述确认矩阵进行拆分,得到互联矩阵
(5)
通过上述例子可知:在计算量测与目标的关联概率βjt(k)时,两目标的确认矩阵拆分所得的互联矩阵为8个,随着跟踪目标的增多,通过确认矩阵得到的互联矩阵将以指数形式增长,计算量大幅增加。
2 Hopfield神经网络
Hopfield神经网络是由美国加州理工学院的Hopfield教授于1982年提出的,是一种单层反馈神经网络,具有离散性和连续性的两种网络模型。[9]在解决优化问题时,采用的均为连续性Hopfield网络。引入系统能量函数,通过对能量函数进行微分处理来使得能量函数及优化问题被最小化。用模拟电路实现的连续性Hopfield网络见图2。
每个神经元由一个运算放大器和相关的元件组成,其输入一方面由输出的反馈组成,另一方面也有
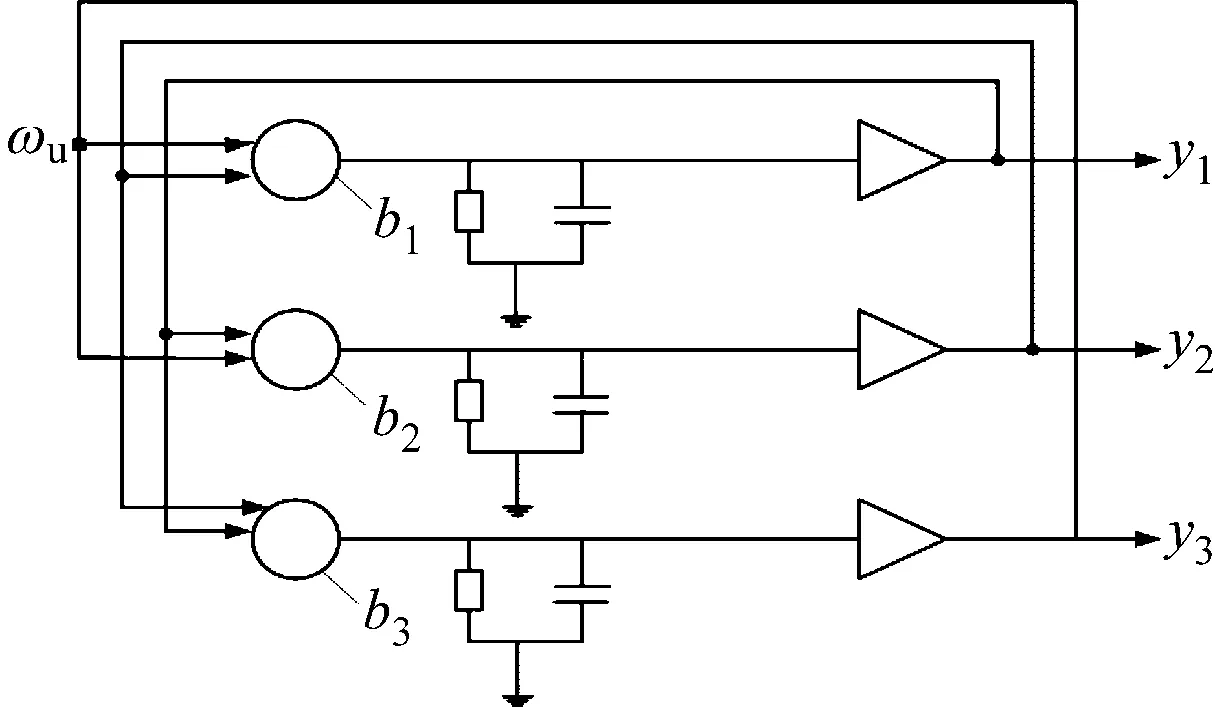
图2 模拟电路实现的连续性Hopfield网络
以电流形式从外界连接进来的输入,以b1、b2、b3如图2所示。根据基尔霍夫电流定律,
(6)
式(6)中:Ci为运算放大器的电容;Ri0为对应电阻的阻值;ui为运算放大器的输入电压;yj为输出电压。令
(7)
式(7)在连续性Hopfield网络中引入能量函数为
(8)
由于式(8)中第二项计算繁琐且影响不是很大,通常通过控制电路参数将第二项忽略:
(9)
对该能量函数进行微分处理为
(10)
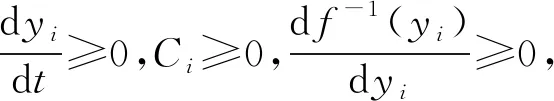
3 Hopfield神经概率数据关联算法
JPDA由于在拆分矩阵时,在跟踪目标以及回波数量增多的情况下,可行事件将以指数形式增长,计算量也随之增加,实时性较差。对此,针对无人船雷达目标跟踪提出一种性能更加优化的神经网络H-JPDA来进行海面雷达的目标跟踪,在目标附近存在密集杂波或者多个目标航迹交叉时,仍能较好地实现最佳的跟踪效果。
联合概率数据关联的求解实质上得到量测j与目标T互联的概率βjt(k)[10],类似于Hopfield神经网络解决旅行商问题(Travelling Salesman Problem,TSP)的组合优化,两者对比见表1。针对其计算量的复杂程度,Hopfield神经概率数据关联将对其简化处理。

表1 JPDA与TSP对比
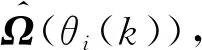
(11)
(12)
式(12)中:ρjt为Pjt(k)的归一化值,即
(13)
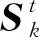
因此,求解神经网络数据关联的概率为
(14)
为方便进行仿真,将式(9)写为
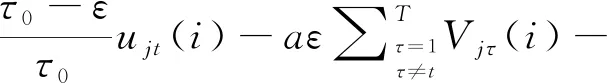
dε[d+e(T-1)]Vjt(i)-
(15)
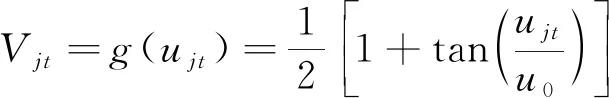
(16)
Vjt初始条件为
(17)
ujt初始条件为
(18)
式(18)中:δujt常采用随机扰动的方法,为区间[-0.1u0,0.1u0]的随机变量。[12]
综上,H-JPDA算法步骤:
1) 利用初始条件,根据式(12)和式(13)得ρjt(k)和Pjt(k),j=0,1,2,…,mk;t=1,2,…,T。
2) 由式(18)ujt的初始值,再利用式(13)求得ujt(i+1)。
3) 由式(17)Vjt的初始值,再利用式(16)求得Vjt(i+1)。
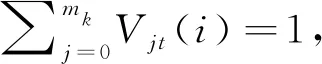
5) 由互联概率βjt(k),利用卡尔曼滤波进行跟踪滤波,对下一时刻状态向量预测和量测向量预测。
4 仿真结果
4.1 仿真参数设计
为验证Hopfield神经网络联合概率数据关联算法的有效性,对两目标进行仿真分析[13],运动过程中发生航迹交叉,目标A初始位置和目标B初始位置和初始运动状态见表2。

表2 目标A、目标B初始位置和运动状态
Hopfield神经网络联合概率数据关联参数,采样次数n=50,采样间隔t0=1 s,蒙特卡洛仿真次数Mc=20,杂波密度λ=2×10-6km-2,门限g=10,检测概率PD=0.98,量测落入跟踪门的概率Pg=0.99,时间步长ε=0.000 01 s,目标数T=2,采样间隔t0=1 s。系统过程噪声协方差为
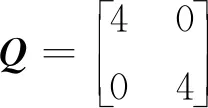
(19)
观测矩阵

(20)
状态转移矩阵
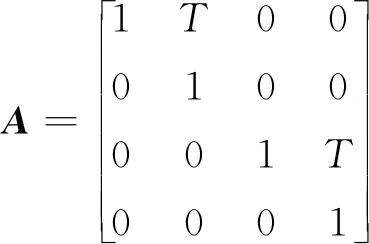
(21)
系统过程噪声矩阵
(22)
Hopfield神经网络能量函数参数对网络的变化相当敏感,原则上不能随意改变,取a=b=d=500,c=200,e=10,u0=0.2。这种选择是考虑参数值较小时,容易获得合法路径;参数值较大时,可增加路径长度的权重,从而使合法路径趋于最优;u0是放大器的增益,参数值太小时,阈值函数接近于符号函数,不能获得较好的解;参数值太大时,S型阈值函数过于平坦,神经元状态不易于收敛到0和1,从而获得合法路径的概率。[14]
4.2 仿真分析
仿真环境为处理器Inter(R)Core(TM)i7-7500U CPU@2.70GHz 2.90 GHz,8.00 GB内存。仿真平台为MATLAB 2017b。[15]目标的实际运动轨迹以及联合概率数据关联下的目标的观测和估计运动轨迹分别见图3和图4。测量值与估计值之间的均方差见图5。滤波值与估计值的均方差同测量值与估计值的均方差之间的比值见图6。MATLAB平台仿真得到JPDA与H-JPDA运行时间比较见表3。由表3可知:基于Hopfield神经网络联合概率数据关联运行时间明显优于联合概率数据关联,提高目标跟踪的速率以及目标跟踪的实时性。
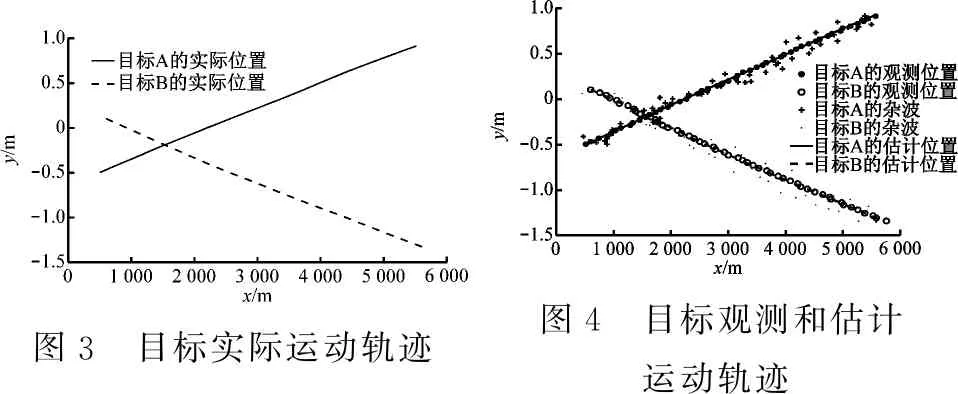
图3 目标实际运动轨迹 图4 目标观测和估计运动轨迹
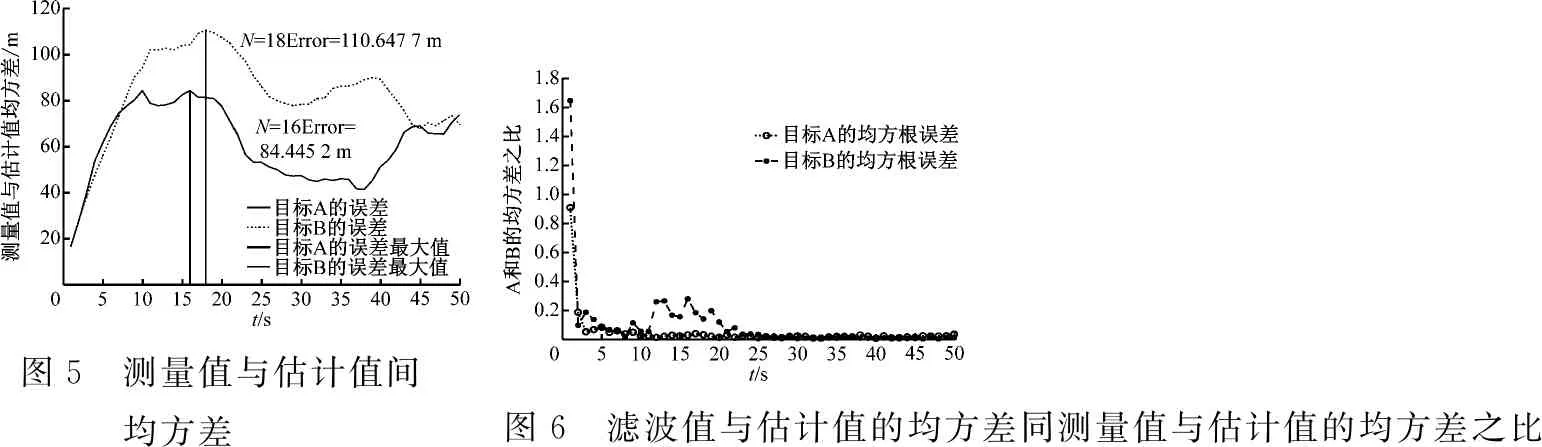
图5 测量值与估计值间均方差图6 滤波值与估计值的均方差同测量值与估计值的均方差之比

表3 JPDA与H-JPDA运行时间比较
5 结束语
本文针对海上船舶雷达多目标跟踪轨迹数据关联问题,提出基于Hopfield神经网络的联合概率数据关联算法,该算法充分考虑到联合数据关联随着目标增多对跟踪精度和实时性的影响。依据Hopfield神经网络自适应性和数据拟合能力等优势,研究表明:该算法可较好地解决在密集杂波情况下的多目标跟踪领域问题,在保证目标跟踪实时性及跟踪精度的情况下,同时可大幅度减少计算量。在目标增多的情况下,该算法的优势会更加明显。基于改进联合概率数据关联算法为多目标跟踪算法提出一种新思路。将该方法应用于雷达使用中,可提高雷达的跟踪精度,增加航行安全。

