温度变化对深基坑钢管支撑温度效应影响分析

陆善佳

(上海市城市建设设计研究总院(集团)有限公司，上海 200120)

0 引言

钢管支撑在地下结构中作为支撑体系而越来越被广泛应用，它的优点在于安装和拆卸方便，安装后可立即进行基坑开挖工序，与钢筋混凝土支撑相比，它不需要进行支模、浇筑及养护等工序，可加快施工进度，故而经常用于基坑抢险工程中，并且钢支撑可循环利用，从而大大的降低了工程造价。

任何物体材料在受冷或者受热后，必然会发生热胀冷缩现象，使得物体材料内部发生应力重分布。通常情况下，深基坑工程内支撑会因为支撑材料、长度和支撑约束形式等因素的不同，支撑受到温度效应的影响程度也有所差异。一日当中因为支撑温度变化而使得钢管支撑的轴力变化达到数吨之多，工程设计人员在项目分析过程中往往可能忽视支撑的温度作用，从而可能做出错误的判断，影响到基坑工程的施工甚至可能造成安全事故[1]。因此，钢管支撑温度效应应当引起工程界的足够重视。在涉及基坑规范[2-3]中的条文规定，当温度改变引起的支撑结构内力不可忽略不计时，应考虑温度应力，然而规范中均未提供具体计算公式，但规范[3]对长度超过40 m的支撑提出了宜考虑10%～20%的支撑内力变化影响。但是对于面积大且深的基坑，按照现行规范进行设计还存在较大的风险。

Chapman等[4]基于弹性半空间基本原理，结合现场实测数据提出了多层水平支撑温度应力解析公式，但解析公式无法将各层支撑轴力差别区分开，所以不适用于存在温度梯度深基坑工程。Attard和Setunge[5]提出在地墙的深基坑围护中采用锚杆注浆，其轴力与变形和温度存在一定的关系。胡蒙达[6]利用弹性力学的热应力理论讨论了钢支撑在变温Tr条件下的热应力σ和相应的轴力变化ΔN计算公式，并通过案例计算温度升高1 ℃下支撑轴力增加值。王 宝等[7]通过现场监测数据，建立基坑围护结构变形与温度之间的关系式，同时也分析了附加变形对基坑稳定性带来的不利影响。陈 峰、艾英钵[8]考虑到变温沿管壁的分布情况，结合化工原理中关于温度传导分布的理论，最终给出了温度应力引起轴力变化的计算公式。本文主要研究钢支撑在考虑轴向变形的情况下，受温度应力作用对基坑支撑结构内力的影响，并给出理论值、数值解和实测数据的差别，以期望对实际基坑工程设计提供参考依据。

1 理论计算模型

当钢管支撑受到太阳直射时，其表面吸收热量使得温度升高，外表面温度向内表面传递，同样使得钢管支撑内部温度升高。但由于在能量传递的过程中存在能量损耗，使得内外表面形成温差，并且温差只发生在钢管支撑的径向，长度方向假设温度相等。如图1所示，钢支撑的横截面空心圆筒，内外径分别为R2和R1。

图1 钢支撑截面示意图

图2 钢支撑示意图

一个弹性体受到温度作用，假设两端自由，则在弹性体内部将产生线应变αΔt。其中：α是弹性体的温度线膨胀系数，Δt为温度变化值，即t1时刻瞬时温度与t0时刻瞬时温度的差值。

圆柱坐标系中以极径r、极角θ和轴向距离z确定空间某一点M(r,θ,z)。当不考虑外力的情况下，体力的径向分量R和轴向分量Z都为0，空间轴对称物体的平衡方程[9]为：

(1)

由线性热应力基本理论可知，钢支撑应变是由应力和温度变化Δt共同引起的，假设Δt只是r的函数，与轴向坐标z无关，因此剪切应力τrz=0，则平衡方程可以简化为：

(2)

由上述公式可得：

(3)

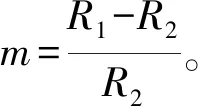
(4)

2 深基坑工程案例分析

2．1 工程概况

天津市河北区新开河调蓄池位于河北区新开河河道内，基坑平面尺寸约为126 m×47．4 m，基坑深度约为15．0～19．8 m，采用明挖法施工。围护结构采用1000 mm厚地下连续墙，钢支撑采用φ800×20钢管撑。河北区属于暖温带半湿润大陆性季风型气候，受季风影响区内四季分明，冬夏与春秋季温差较大，冬夏较长，春秋较短，年平均气温11～12 ℃，年降水量550 mm。基坑土体开挖至浇筑底板时间跨度为2018年8月至2019年1月，期间气温变化情况如图3所示。

图3 基坑开挖期间气温变化情况

基坑呈矩形状，墙顶以下2．55 m处设置一道钢筋混凝土支撑，其余设置三道钢管支撑，钢支撑总长度为l=45．4 m，支撑水平间距S=4 m，支撑R1=400 mm，R2=380 mm，钢材弹性模量Es=206×103N·mm-2，混凝土弹性模量Ec=3．0×104N·mm-2，温度线膨胀系数α=11×10-6·℃-1，泊松比μ=0.31，基坑开挖期间，天津市河北区的月平均最高、最低气温变化趋势如图3所示。

2．2 解析解

对式(4)迭代计算结果如表1所示。

表1 计算结果

注：Δl负值为地墙向坑外变形，正值为地墙向坑内变形。

2．3 有限元分析

为更真实地模拟实际支撑受力状况，在单根支撑两端施加轴向位移约束，具体位移约束取值为基坑开挖期间，地下竖向水平位移日平均变化值。图4为基坑土体开挖期间(当年8月至次年1月)的侧向变形监测数据。

图4 基坑开挖期间地墙测斜累计变形值

由图4可得，埋深在7．5 m及12 m位置地墙侧向位移日变化最大值Δδ分别为+0．140 mm和+0．131 mm(+表示向坑内变形)。

为更深入探究温度对钢支撑支护系统的影响，利用通用有限元软件建立二维模型，采用整体水平框架简化计算模型，如图5所示。将2．1节中施工期间的温度荷载施加在钢支撑上，并与现场监测数据、理论解析解分别进行对比。地连墙和钢支撑采用弹性模型，均采用线单元。钢支撑的收缩系数取α=11×10-6·℃-1，为简化计算，在支撑上逐级施加温度荷载。

图5 有限元模型

由有限元模型计算可得表2计算结果。

表2 数值分析计算结果

2．4 实测结果与分析

将现场围护墙侧向位移监测数据代入公式(3)得出不同时间段的解析解并与现场实测钢支撑轴力值进行对比，如表3所示。

通过对表3对比分析，温度每升高1 ℃，数值解的支撑轴力分别增加6．55 t、6．76 t、7．06 t、6．88 t、6．37 t、6．75 t；实测支撑轴力分别增加5．90 t、6．30 t、6．20 t、6．40 t、5．90 t、6．30 t；本文在文献[8]中公式基础上改进后的公式(4)所得解析解，温度每升高1 ℃，支撑轴力增加8．2 t。由解析公式计算的结果偏于保守，在今后基坑围护设计过程中可作为安全储备。

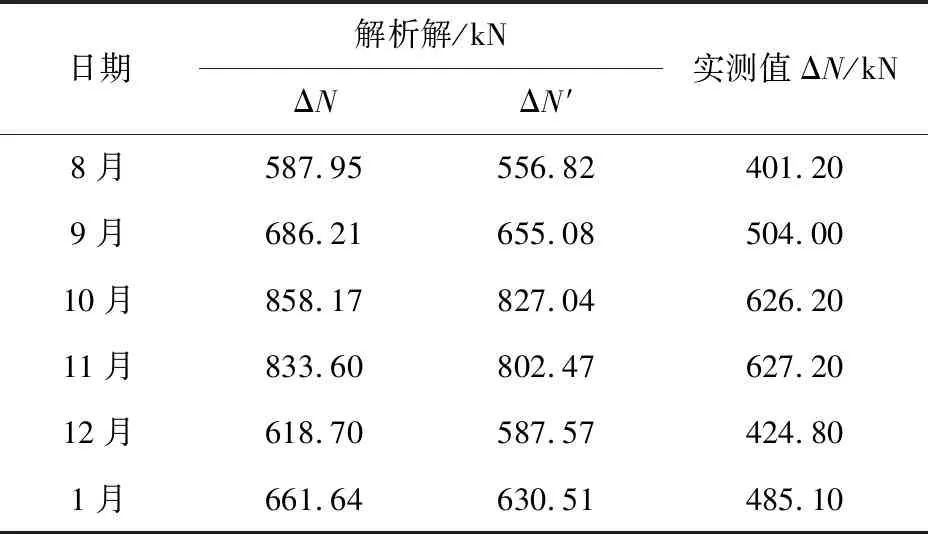
表3 实测值与解析解对比表

3 结论

以某深基坑工程为背景，基于弹性热力学基本理论，研究温度变化对深基坑钢管支撑轴力的影响，可以得出以下结论：

(1)钢管支撑轴力变化的幅度与温度变化相吻合；现场轴力监测数据可知，温度每升高1 ℃使得钢管支撑轴力的增加高达6．17 t，由此可见，温度变化对钢管支撑轴力的影响是很大的，应当引起工程师的注意。

(2)在设计过程中，对于昼夜气温变化较大的地域或者跨季节施工的深基坑工程，应当在计算中考虑温度荷载作用，对钢支撑适当选取具有足够安全储备的钢支撑，以此来抵抗升温引起的轴力增加。同时，在基坑开挖过程中，对于钢支撑，夏季可以采取有效的遮挡、水淋等降温措施，冬季可以采取“穿棉衣”等保温措施，尽可能地减少因为温差引起的安全隐患。

(3)本文对工程实际案例进行分析，进而证明解析公式的正确性，做到理论结合实际，便于帮助工程师们考虑温度效应。