基于人工蜂群径向基神经网络预测参考作物需水量

孟 玮 ，孙西欢,2，郭向红，马娟娟，马文云，赵文渊，张威贤

(1.太原理工大学水利科学与工程学院，太原 030024；2.晋中学院，山西 晋中 030600)

0 引 言

针对山西省水资源紧缺和水土流失严重的现状，孙西欢提出了一种适合于我国北方果园的灌溉方法，即蓄水坑灌法[1]。目前，关于蓄水坑灌法已做了大量的研究，其研究成果主要集中在蓄水坑灌田间技术参数的研究[2]，土壤水分运动的试验及模拟[3]，水氮运移及模拟研究[4]，果树需水量试验及模拟等方面的研究[5]。日参考作物需水量ET0由气象因子所决定，是反映不同地区、不同时期大气的蒸散能力的重要指标，是计算作物蒸散量的重要参数之一。有效且准确地预测蓄水坑灌条件下的日参考作物蒸散量，对于研究蓄水坑灌果树需水量具有重要意义，同时对于制定蓄水坑灌果树合理高效灌溉制度提供了理论依据。

由于ET0在制定作物灌溉制度过程中的重要作用，国内外学者采用利用人工智能网络[6]，最小二乘向量机[7]，及基于优化算法的神经网络[8,9]等不同模型对ET0进行了模拟预测，并对其适用性进行了评价与比较。目前，利用基于仿生智能优化算法的人工智能网络模型对蓄水坑灌果园日参考作物需水量的预测模拟研究较少，该方法是否适合于蓄水坑灌果园日参考作物需水量的预测仍有待进一步研究。因此，本文构建了基于人工蜂群优化算法的径向基神经网络预测模型，以FAO56-PM公式的计算结果为标准分析该预测模型的适用性，以期为山西省农业科学院果树所蓄水坑灌苹果园的农田水分优化管理提供指导。

1 理论与方法

1.1 研究区概况

本文研究区是中国山西省农业科学院果树所蓄水坑灌果园试验基地。该试验基地位于山西省晋中市，地处北纬37°23′，东经112°32′，平均海拔为781.9 m，年平均气温9.8 ℃，年平均降雨量459.6 mm，无霜期175 d，属典型的黄土高原地区暖温带大陆性季风气候，冬春季受极地干冷气团影响，寒冷干燥多风沙；夏秋季受西太平洋副热带高压和印度洋低压影响，炎热多暴雨。土壤类型主要为粉沙壤土，平均密呀为1.47 g/cm3，该试验基地的光热资源比较适宜果树种植。本文所用数据为2016-2017年的逐日气象数据：其中包括日平均气温Tmean、参考高度处风速v、大气相对湿度RH、净辐射Rn。

1.2 ET0计算公式

FAO56-PM公式表达式如下[10]：

(1)

式中：ET0为参考作物蒸散量，mm/d；Δ为饱和水汽压梯度，kPa/℃；Rn为净辐射，MJ/(m2·d)；G为土壤热通量，MJ/(m2·d)；γ为空气干湿表常数，kPa/℃；T为日平均气温，℃；u2为2 m高处的风速，m/s；es、ea分别为饱和水汽压和实际水汽压，kPa。

1.3 径向基神经网络模型

径向基函数(Radial Basis Function)神经网络是一种单隐层的三层前馈网络，分别由输入层，隐含层及输出层组成。输入层到隐含层之间的连接权值为1。隐含层到输出层之间有连接权值，从隐含层到输出层的映射是线性的，即整个网络的输出是隐含层输出结果的线性加权之和。RBF神经网络具有局部逼近和最佳逼近性能。

输入层：输入节点的个数为输入样本的维度。该层主要是将输入样本传递给隐含层。在此之前，为了提高预测结果的精度，需要对输入的样本数据做标准化处理，以避免因不同量纲的问题对预测结果造成影响。设有N个样本：

X=(X1,X2,…,XN)T

(2)

隐含层：隐含层是非线性的，将输入向量空间转换到隐含层空间，使得原来线性不可分的问题变得线性可分。RBF神经网络与其他前馈神经网络不同的地方主要是隐含层。隐含层空间的“基”采用径向基函数，该函数是对中心点径向对称且衰减的非负线性的局部响应函数，一旦各隐含层节点的径向基函数的中心确定，不需要通过权值连接就可以将输入向量空间映射到隐含层空间。假设隐含层的节点数为J，隐含层则是通过映射将I维的输入矢量映射到J维空间内。隐含层第j个神经元的输出为：

(3)

式中：cj是第j个神经元的中心，cj的维度与输入节点的个数是相同的，也是一个I维向量；σj是第j个神经元的宽度，反映了径向基函数的衰减速度，σ越大，隐含层神经元宽度越宽，径向基函数就衰减得越慢，反之亦然；‖·‖是欧几里得距离；φ(·)是径向基函数，本文选择的是高斯函数。

输出层：从隐含层到输出层的映射函数是一个线性函数，通过连接权值对隐含层各层输出结果的线性组合，其输出结果表达式如下：

(4)

式中：ωjk是第j个隐含节点到第k个输出节点的连接权值；hj(X)为隐含层神经元的输出结果。

1.4 评价指标

本文中数据分析与计算采用MATLAB R2014b软件，图表制作采用excel软件。采用线性回归斜率、相关系数R2、均方根误差RMSE、平均相对误差MAPE来衡量预测值与标准值之间的一致性，以量化模型性能。其计算公式表达如下：

(5)

(6)

式中：Pi、Oi分别表示标准值和模型预测值；N为观测总数。

2 ET0预测模型构建

2.1 数据集

模型中数据集分成两个子集：训练集及测试集。训练集为2016年的逐日数据，共366个样本，训练集的输入样本为2016年的逐日气象数据，主要包括净辐射Rn、大气相对湿度RH、风速v、日平均温度Tmean；训练集的输出样本为2016年日作物参考需水量ET0。测试集为2017年的逐日数据，共365个样本，其中2017年10月2日-11月1日的数据(共31个样本)因仪器出现问题而造成部分数据有缺失，因此剔除，剩余334个样本，测试集的输入样本为2017年内334个样本的逐日气象数据，主要包括净辐射Rn、大气相对湿度RH、风速v、日平均温度Tmean；测试集的输出样本为2017年内334个样本的日作物参考需水量ET0。

2.2 人工蜂群算法原理

人工蜂群算法(ABC, Artificial Bee Colony Algorithm)是由Karaboga[11]提出的，之后被应用于神经网络训练领域，利用人工蜂群算法进行反馈神经网络训练，寻找最优权重集合[12]，对数据集进行分类[13]，该方法不仅提高了准确率而且减少了人工神经网络点数量[14]。径向基神经网络不仅具有局部逼近性能和最佳逼近性能，而且具有一定的收敛能力、泛化性能、鲁棒性能等。ABC算法具有较强的全局收敛能力。将两者结合起来，不仅能提高径向基神经网络网络的泛化性能和鲁棒性能，还能提高神经网络的学习能力及收敛速度。

蜜蜂的群智能行为中包括3个基本的组成要素：蜜源、雇佣蜂和非雇佣蜂。蜜源：相当于优化问题的可行解。雇佣蜂，即引领蜂，其数量与蜜源数量相等，具有记忆功能，将搜索到的蜜源相关信息存储并分享给其他的蜜蜂。非雇佣蜂包括侦察蜂和跟随蜂，侦察蜂在蜂巢周围搜索附近新的蜜源，跟随蜂则观察引领蜂的舞蹈进行选择并跟随，蜂群中的跟随蜂和引领蜂的数量相等。主要步骤如下所示：

在搜索空间内随机产生蜜源i的初始位置：

xid=Ld+rand(0,1)(Ud-Ld)

(7)

引领蜂在蜜源i的周围按下式搜索一个新蜜源：

vid=xid+φ(xid-xjd)

(8)

当新蜜源xid的适应度优于vid时，采用贪婪选择方法用新蜜源代替原来的蜜源，否则保留xid，跟随蜂根据引领蜂分享的蜜源信息，按下式计算概率并进行跟随。

(9)

在搜索过程中，如果蜜源Xi经过t次迭代搜索到达阈值limit而没有找到更好的蜜源，该蜜源Xi就会被放弃，与之对应的采蜜蜂的角色变为侦察蜂。侦察蜂将在搜索空间随机产生一个新的蜜源代替Xi。

2.3 基于人工蜂群算法的径向基神经网络

本文提出的基于人工蜂群算法优化径向基神经网络(ABC-RBF)的具体训练步骤如下：①建立一个RBF神经网络模型并初始化。②初始化人工蜂群算法中的相关参数。设定蜂数量为N，限制迭代次数L，最大迭代次数M。③按式(7)随机生成N个蜜源，引领蜂则按式(8)在对应蜜源附近搜索新蜜源，并依照式(9)计算收益度，从而根据贪婪算法判断是否替换原有蜜源。④判断蜜源Xi的局部搜索次数是否超过限制迭代次数L，若超过，则第i个引领蜂转化为侦查蜂，按式(8)全局随机搜索新蜜源。 ⑤记录当前全局最优蜜源，即全局最优解。⑥如果人工蜂群算法迭代次数超过设定的最大循环次数M，那么RBF神经网络将结束学习训练，否则返回到第③步。⑦将得到的最优蜜源解码变为RBF神经网络中的最优参数，继续用得到的数据训练REF神经网络，从而达到预测蓄水坑灌下参考作物需水量的目的。

3 结果与分析

3.1 模型预测结果及分析

本文中径向基神经网络模型对蓄水坑灌果园日参考作物需水量的模拟结果见图1、图2。图1为RBF模型预测值与FAO56-PM标准值的线性关系，图2为 RBF模型预测的绝对误差。RBF网络结构中的隐含层神经元个数为MN=26，径向基的扩展速度(中心宽度)为spread=2.0，均方误差goal=0。径向基神经网络模型对ET0的模拟结果为：相关系数R2=0.92，均方根误差RMSE=0.56，平均相对误差MAPE=12.63%。本文中基于人工蜂群算法优化径向基神经网络模型对蓄水坑灌果园日参考作物需水量的模拟结果见图3、图4。图3为ABC-RBF模型预测值与FAO56-PM标准值的线性关系，图4为 ABC-RBF模型预测的绝对误差。基于人工蜂群算法优化径向基神经网络模型对ET0的模拟结果为：相关系数R2=0.94，均方根误差RMSE=0.46，平均相对误差MAPE=11.28%。由图2和图4可看出：两个模型在预测日序数为270～274 d的蓄水坑灌果园日参考作物需水量时均存在较大的绝对误差，2017年10月2日-11月1日(日序数为275～305)的数据因仪器出现问题而造成数据有缺失，因此可能在第270～274 d时仪器就已经出现了基础气象数据记录不准确的现象，所以造成了两个模型在第270～274 d中预测的绝对误差均超过了3%的现象。

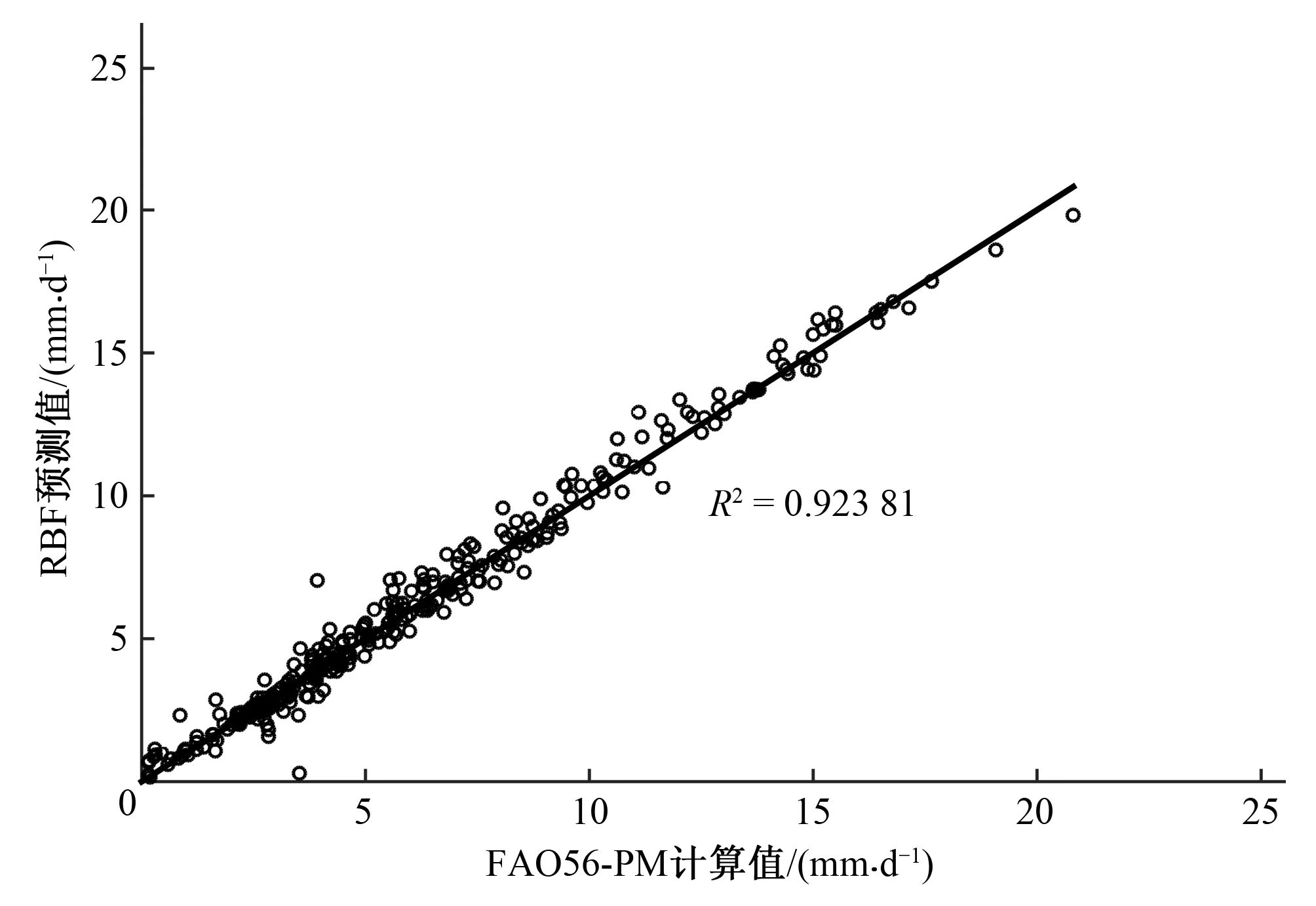
图1 RBF模型预测值与FAO56-PM标准值的线性关系Fig.1 Linear relationship between RBF predicted values and FAO56-PM standard values

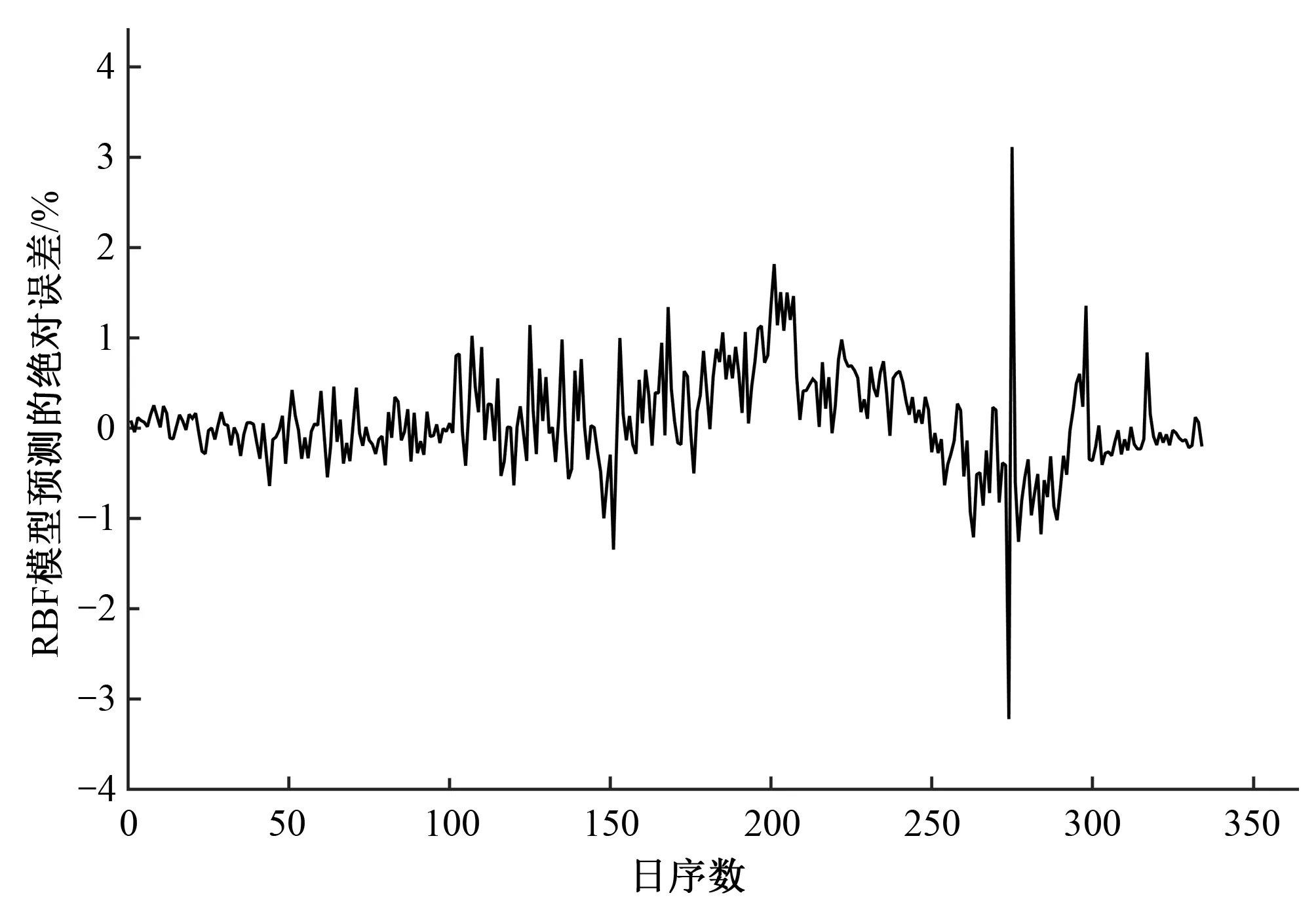
图2 RBF模型预测的绝对误差Fig.2 Absolute error predicted by RBF model

图3 ABC-RBF模型预测值与FAO56-PM标准值线性关系Fig.3 Linear relationship between ABC-RBF predicted values and FAO56-PM standard values

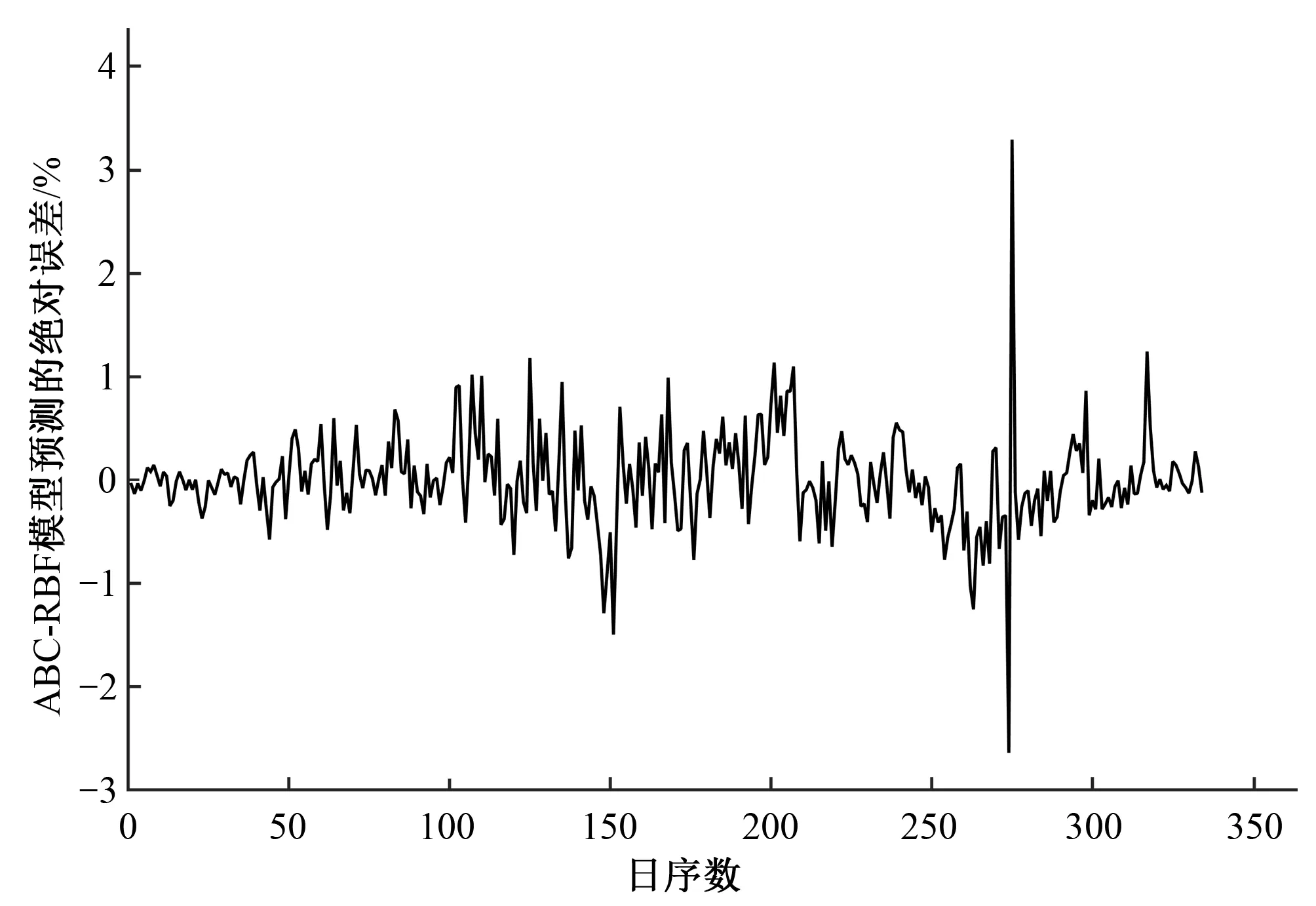
图4 ABC-RBF模型预测的绝对误差Fig.4 Absolute error predicted by ABC-RBF model

两种不同模型预测值与FAO56-PM标准计算值的t配对检验结果见表1。由表1可知，RBF和ABC-RBF两个模型对蓄水坑灌果园日参考作物需水量的预测值与FAO56-PM标准值之间均无显著性差异，由于ABC-RBF模型中的RMSE和MAPE比RBF模型中的RMSE和MAPE值小，说明ABC-RBF模型的预测值更接近FAO56-PM标准计算值，其预测效果也相对较好。因此在今后蓄水坑灌果园日参考作物需水量的预测中，建议采用本文提出的ABC-RBF模型。

表1 两个模型预测值与FAO56-PM标准值的t配对检验结果Tab.1 Paired test results of standard and calculated values for two different methods

3.2 蓄水坑灌果园日参考作物需水量趋势分析

本文应用FAO56-PM公式对山西省农业科学研究院果树所蓄水坑灌果园试验基地2017年的日参考作物需水量ET0进行计算，其计算结果见图5。由图5可知，逐日ET0的变化趋势呈现单峰变化趋势，先增大后减小，这与当地的气象特征有关。图6为RBF模型对蓄水坑灌果园日参考作物需水量ET0预测的变化趋势图，图7为 ABC-RBF模型对蓄水坑灌果园日参考作物需水量ET0预测的变化趋势。综合图5～图7可知：蓄水坑灌果园的日参考作物需水量的变化特征如下：即在4-6月呈上升趋势，在7月达到峰值，8-9月呈下降趋势。

图5 FAO56-PM对蓄水坑灌果园日参考作物需水量ET0计算的变化趋势Fig.5 The change trend of the reference crop water requirement of the water storage pit irrigation orchard by FAO56-PM method

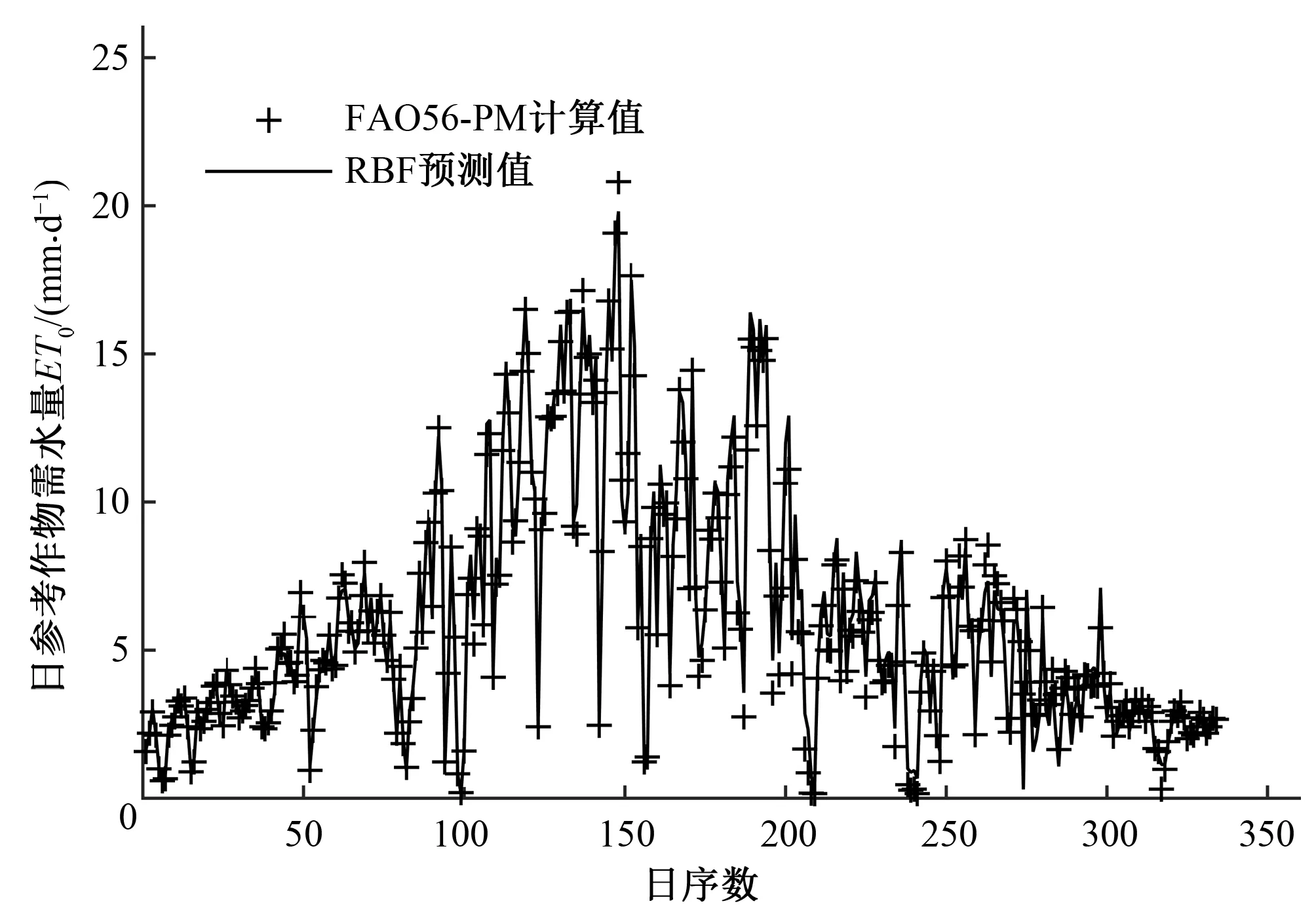
图6 RBF模型对蓄水坑灌果园日参考作物需水量ET0预测的变化趋势Fig.6 The change trend of the reference crop water requirement of the water storage pit irrigation orchard by the RBF model

图7 ABC-RBF模型对蓄水坑灌果园日参考作物需水量ET0预测的变化趋势Fig.7 The change trend of the reference crop water requirement of the water storage pit irrigation orchard by the ABC-RBF model

4 结 论

本文以山西省农业科学院果树所蓄水坑灌试验基地日气象资料为基础建立了基于人工蜂群算法优化径向基神经网络的ET0预测模型。研究结果表明：RBF和ABC-RBF模型在模拟蓄水坑灌果园日参考作物需水量时的均方根误差分别为0.56和0.46 mm/d，相关系数分别为：0.92和0.94。因此，在估算山西省农业科学院果树所蓄水坑灌苹果园日参考作物蒸散量时推荐选用ABC-RBF模型。在后续研究中应以蓄水坑灌果园的蒸散实测值为预测目标，建立基于ABC-RBF的蓄水坑灌果园的蒸散预测模型，以期为蓄水坑灌果园水分管理以及蓄水坑灌下作物需水量预测提供较为准确的依据。