考虑局部遮挡的太阳能无人机能源控制
刘刚,王正平,刘莉,张晓辉,曹潇
北京理工大学 宇航学院,北京 100081
太阳能无人机是将太阳光转换为电能作为其能量来源[1],为了满足无人机飞行性能需求,太阳能无人机一般采用太阳能电池与蓄电池混合能源的方式[2],能源管理与控制是其关键技术之一。
能源管理的目标是充分利用各能源优势,提高混合能源系统效能。能源管理策略可分为基于规则的策略和基于优化的策略[3-5]。基于规则的能源管理策略已广泛应用于混合动力汽车工业[4]。基于优化的能源管理策略思路是根据目标函数和约束条件,使用优化算法在可行域内进行搜索,使目标函数能够取到最优值或次优值。主要包括全局优化策略(如动态规划[6]等)和非全局优化策略(如等效燃料消耗最小策略[7]等)。太阳能无人机的混合能源管理策略也得到了一定的研究[2,8-10]。
在飞行过程中,飞鸟、云彩等外界因素会对太阳能电池造成遮挡;在日出、日落以及转弯机动过程中,螺旋桨、垂尾、安定面等也会对太阳能电池造成遮挡;这些都会在太阳能无人机的太阳能电池上产生局部阴影现象。在均匀辐照情况下,太阳能电池的功率-电压(P-V)曲线只有一个最大功率点,而局部阴影情况下,由于旁路二极管的存在,太阳能电池的P-V曲线上会存在多个峰值。为了处理局部阴影情况下的多极值问题,研究者提出了多种基于现代优化方法的最大功率点追踪(MPPT)技术[11],进化算法有着较好的表现[12]。萤火虫算法[13]是一种基于群体的寻优算法,具有计算效率高、设置参数少、易于实现等优点[14],目前已广泛应用于图像处理[15]、函数优化[16]、数据挖掘[17]、路径规划[18]等研究领域。2014年,Sundareswaran等[19]采用萤火虫算法,实现了太阳能电池在局部阴影条件下的最大功率点追踪。2015年,Safarudin等[20]提出了简化萤火虫算法,通过不断更新β系数,忽略α和γ系数来简化算法。2017年,Teshome等[21]使用所有萤火虫的平均坐标作为代表点改进萤火虫算法,单个萤火虫仅朝向平均坐标移动,通过减少萤火虫的移动次数来提高跟踪速度。
本文针对太阳能无人机飞行过程中太阳能电池可能出现局部遮挡的问题,开展局部遮挡情况下太阳能电池/蓄电池混合控制研究。首先,对萤火虫算法进行改进,提高太阳能电池阵列功率曲线多极值情况下全局最大功率点的追踪效率;然后,设计考虑局部阴影情况下太阳能无人机的太阳能电池/蓄电池混合能源状态机控制规则;最后,以“蒲公英I”无人机[22]为例,开展仿真分析,验证本文方法的效果。
1 基于改进萤火虫算法的最大功率点追踪
1.1 萤火虫算法的改进
萤火虫算法(Firefly Algorithm, FA)是一种启发式算法,把空间各点看成萤火虫,利用发光强的萤火虫会吸引发光弱的萤火虫的特点,在发光弱的萤火虫向发光强的萤火虫移动的过程中,完成位置的迭代,从而找出最优位置,完成寻优过程。在FA算法中,第i和第j个萤火虫的相互吸引度表示为
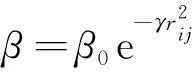
(1)
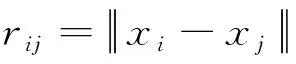
萤火虫i被另一个更有吸引力的萤火虫j所吸引的位置更新公式为
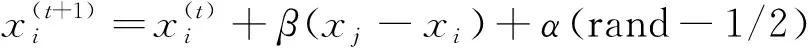
(2)
萤火虫算法中相对吸引度β与2个萤火虫间的距离r和最大吸引度β0相关。较大的β0能使算法快速收敛,但收敛精度较低;较小的β0会使收敛速度变慢,但收敛精度更高。
2个萤火虫间的相对吸引度还与萤火虫的亮度有关[6]。本文提出将发光亮度引入相对吸引度β的计算过程,综合解决收敛速度和收敛精度的问题。改进的萤火虫算法(Modified Firefly Algorithm,MFA)具体为:引进相对亮度差阈值BTH;当2个萤火虫的相对亮度值小于BTH时,相对吸引度β与亮度差无关,采用式(1)计算;当2个萤火虫的相对亮度差大于BTH时,相对吸引度β与亮度差相关,认为当萤火虫i和j之间的距离一定时,其亮度差越大,相对吸引度越大,此时的相对引度计算表达式为
(3)
式中:Bi和Bj分别为萤火虫i和j所对应的亮度;θ为亮度缩放因子。
通过引入BTH,可在搜索过程中针对不同亮度的萤火虫实现参数β的自动调整。在搜索的初期阶段,萤火虫距离较远,亮度差值普遍大于BTH,其β也相对较大,能够提高收敛速度。在搜索的后期,萤火虫距离较近,亮度差值普遍小于BTH,能够对搜索结果进行微小调整,提高收敛精度和输出稳定性。
为使MFA的执行效果最佳,需要对BTH和θ的取值进行精细调整。BTH取值应小于最大亮度的10%,以保证搜索初期大部分萤火虫的亮度差普遍大于BTH;BTH和θ的取值应满足θBTH≥β0。较大的θ使得搜索初期萤火虫能够较快聚集,加快收敛速度,但是过大的θ会导致错过全局最大功率点的可能性增加,因此,θ取值应该从小到大逐渐调整。
1.2 基于MFA的最大功率点追踪方法
在利用MFA进行最大功率点追踪时,萤火虫的位置对应太阳能电池阵列的输出电压Vpv.i,萤火虫的亮度对应该电压下的太阳能电池阵列输出功率Ppv,i,萤火虫的相对亮度差阈值对应功率差阈值PTH。在最大功率点追踪过程中,MFA通过不断调节太阳能电池阵列的输出电压来搜索全局最大功率点。
算法中,初值的选取既要有利于算法较快收敛,又要避免丢失极值点。本文设定初始电压个数与萤火虫数目相同,且均匀分布在整个搜索区间内。初始电压值计算表达式为
(4)
式中:VUB和VLB分别为搜索区域的电压上界和下界;N为萤火虫的数目。
在全局最大功率点的搜索过程中,由于MFA不断更新输出电压,进而导致太阳能电池阵列输出功率的持续波动。在搜索前期,各点的功率相差较大;在搜索后期,各点集中在最大功率点附近。为减小不必要的功率波动,使输出功率能够稳定,采用如下终止策略:当各点的功率差值均小于最大功率误差值ε1时,终止算法,即
|PGbest-Ppv,i|<ε1i=1,2,…,N
(5)
式中:PGbest为已搜索到的全局最大功率;Ppv,i为各个萤火虫的实际功率。
当算法终止后,若光照强度发生变化或者出现局部阴影现象时,太阳能电池阵列的最大功率点会发生移动,这时重新启动算法,进行新一轮的全局最大功率点搜索。引入功率变化量阈值ΔPTH和功率变化量ΔP,当ΔP大于该阈值时重新启动算法。
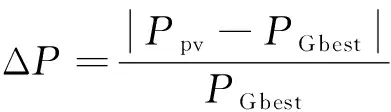
(6)
式中:Ppv为当前太阳能电池阵列的实时功率。
基于MFA的最大功率点追踪控制流程如图1所示,图中Ipv,i为各个萤火虫实际电流。
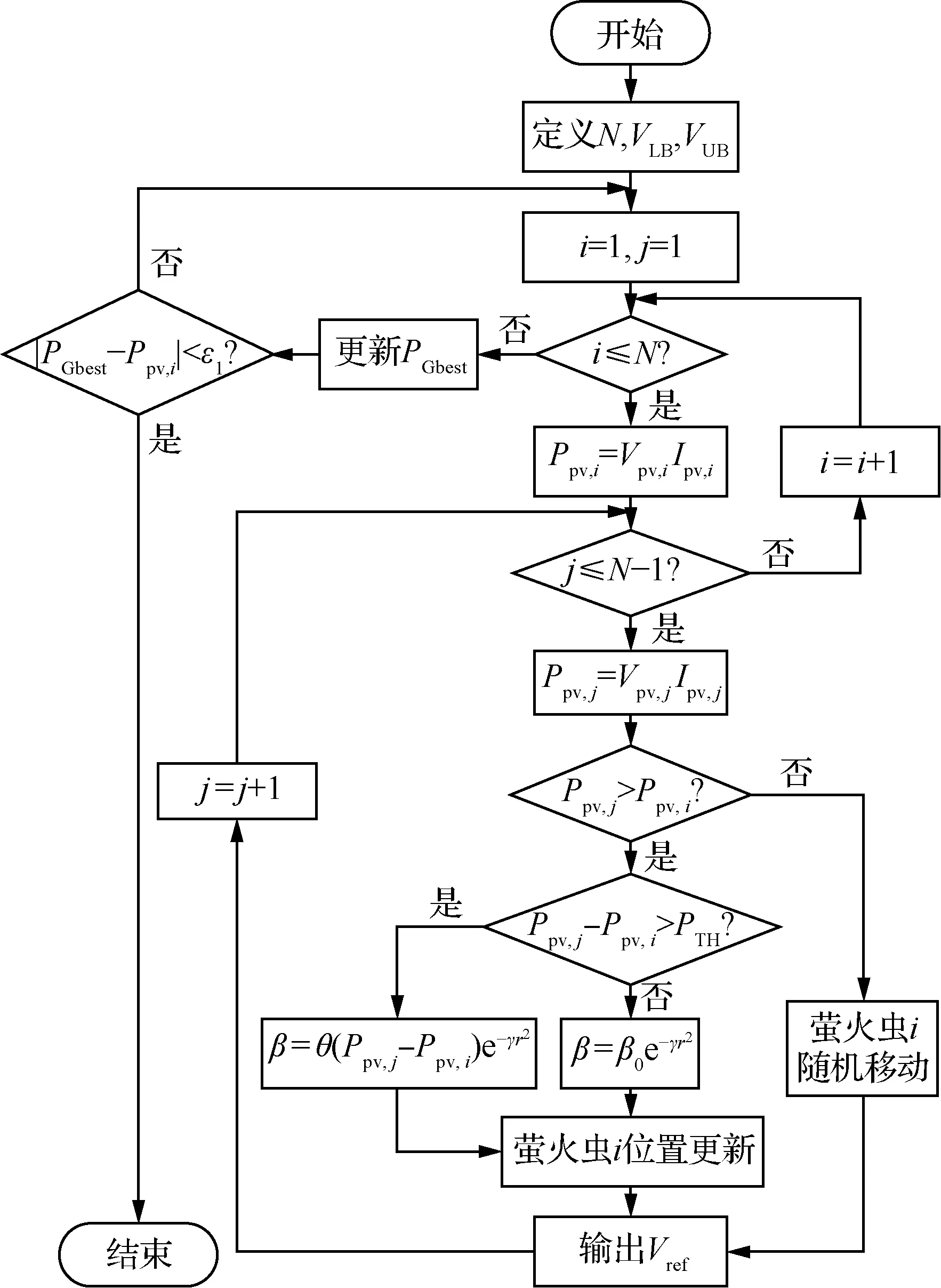
图1 基于MFA的MPPT控制流程Fig.1 Flowchart of MPPT control based on proposed MFA
2 基于状态机的太阳能电池/蓄电池混合能源控制
对于采用太阳能电池/蓄电池混合能源的太阳能无人机,不仅要考虑太阳能电池的最大功率点追踪,还要综合考虑2种能源的管理与功率分配问题。本文采取“独立控制与综合管理”的思路,提出混合能源的管理策略:采用MPPT控制器对太阳能电池最大功率点进行独立控制;同时,实时监测载荷需求和能源系统状态,采用状态机策略从功率层面对太阳能电池输出功率和蓄电池充放电功率进行管理。
混合能源控制基本原则是:太阳能无人机动力系统需求功率由太阳能电池和蓄电池满足,若太阳能电池功率有剩余则为蓄电池充电,保证功率分配满足功率平衡原则。太阳能电池和蓄电池状态主要依据蓄电池剩余电量(SOC)、需求功率(PD)、上一时刻太阳能电池最大功率(Ppvmax)3个状态参数划分。表1为所制定的混合能源状态机策略控制规则表,其中:太阳能电池输出功率Ppv为控制量;PD为需求功率;Ppvmax为太阳能电池最大功率;Pchrg为蓄电池最大充电功率。
为了避免蓄电池出现局部状态陷阱、保证状态间的平滑过渡,在蓄电池电量状态临界点加入状态回滞环[23](见图2),在SOC临界值附近增加状态回滞区域,在该区域内保持上一电量状态,进而解决局部状态反复跳变问题。

表1 状态机能源管理策略规则
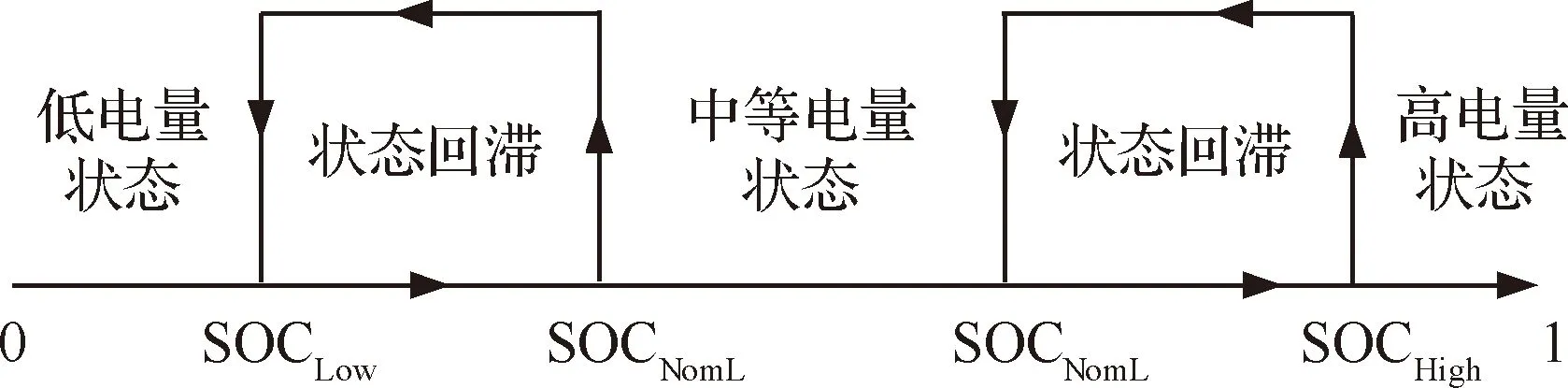
图2 蓄电池电量状态回滞环设计Fig.2 Battery power state hysteresis loop design
基于上述规则,设计状态机能源管理策略控制流程如图3所示。
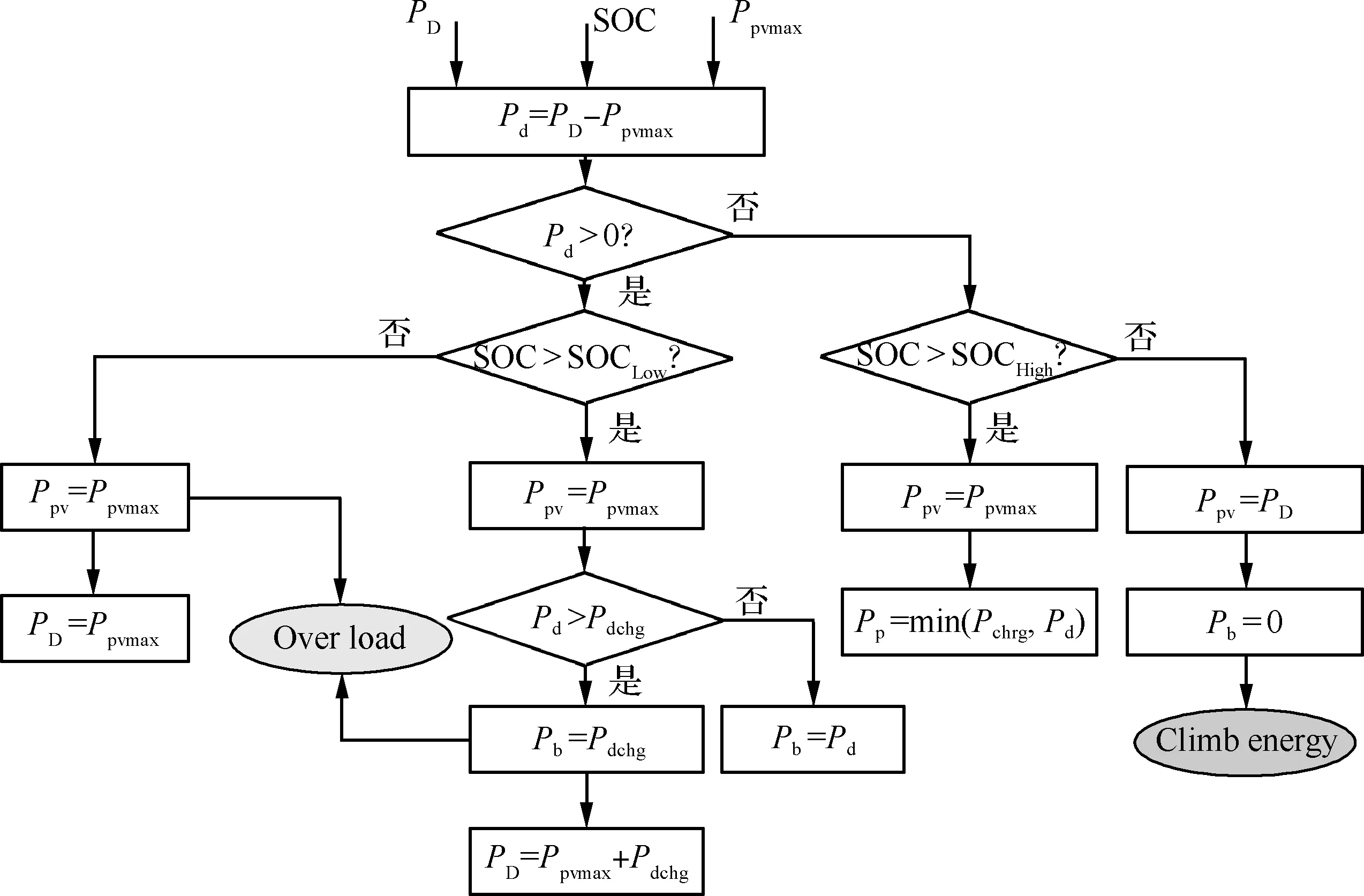
图3 混合能源控制流程Fig.3 Hybrid energy control process
3 仿真与分析
本文以“蒲公英I”无人机[22]为例,采用本文提出的算法和规则,开展太阳能电池局部遮挡情况下最大功率点追踪和混合能源控制的仿真分析。
3.1 仿真条件
3.1.1 太阳能阵列模型
“蒲公英I”无人机采用上单翼、双尾撑、双垂尾的常规布局,翼展6.15 m,分为左、中、右三段,均铺设太阳能电池,有效铺片面积1.875 m2。机翼中段的右半段与机翼右段串联为右太阳能电池阵列(图4),为右侧电机供电;左端同理。
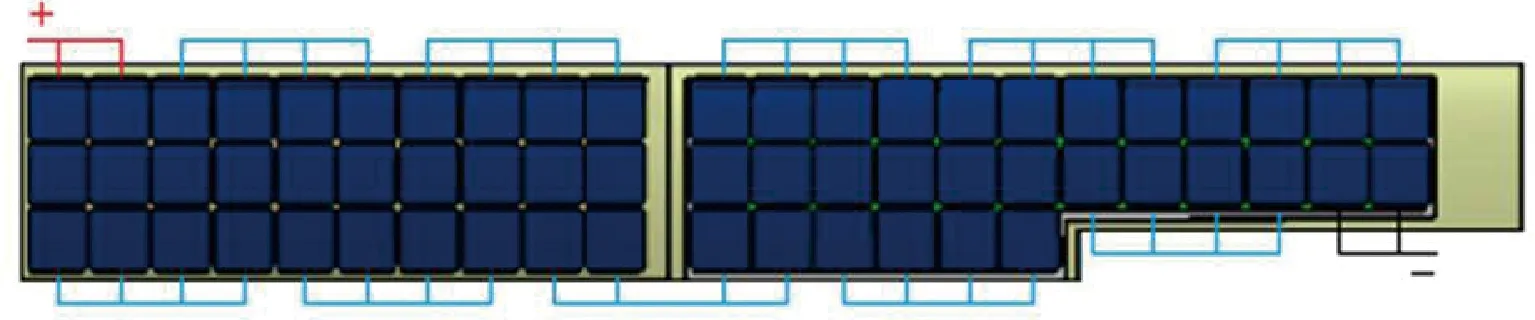
图4 太阳能电池阵列连接示意图Fig.4 Schematic of solar cell array connection
本文以右太阳能电池阵列为例,建立太阳能电池阵列模型。其中:太阳能电池沿机翼弦向串联;相邻两串并联,同时并联一个旁路二极管,构成一个太阳能电池阵列单元;靠近翼根的单元记为PV1,由内向外进行编号,共计11个单元串联在一起形成太阳能电池阵列。每个电池单元视为均匀光照,可通过改变不同单元的光照强度来模拟局部阴影情况。图5为电池阵列仿真模型。
3.1.2 局部阴影模型
为了对比分析局部遮挡问题,设计了3个局部阴影模型,表2给出了对应模型的电池阵列光照情况。
3种光照情况下太阳能电池阵列的P-V特性曲线如图6所示,其中:无阴影情况有一个全局最大功率点,最大功率为230.9 W;局部阴影情况1有2个功率极值点,功率极值分别为208.8 W和175.6 W;局部阴影情况2有3个功率极值点,功率极值分别为184.6 W、159.4 W和126.7 W;2种有阴影情况的全局最大功率点都在最左侧。
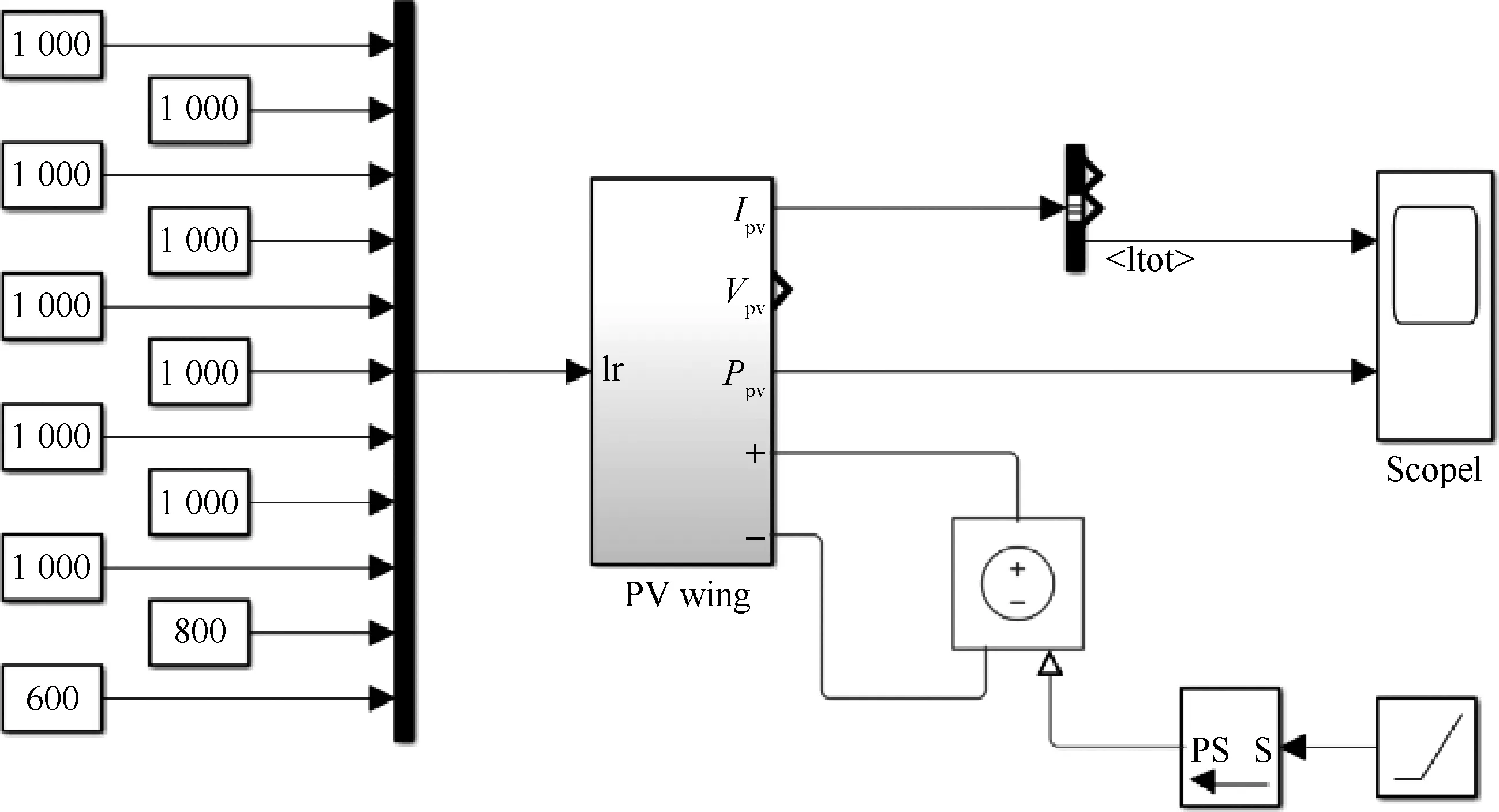
图5 太阳能电池阵列仿真模型Fig.5 Solar cell array simulation model
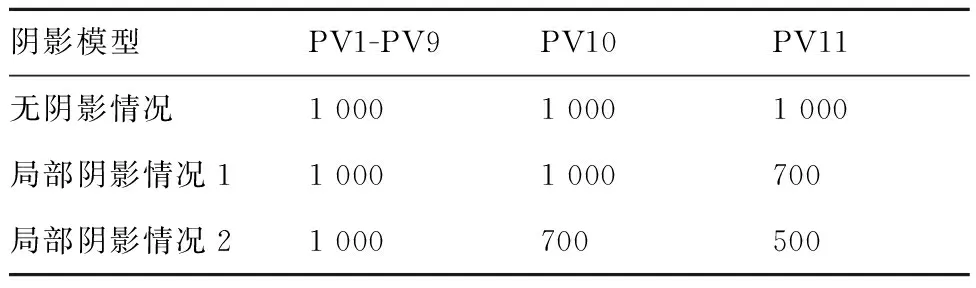
表2 太阳能阵列局部阴影模型光照强度
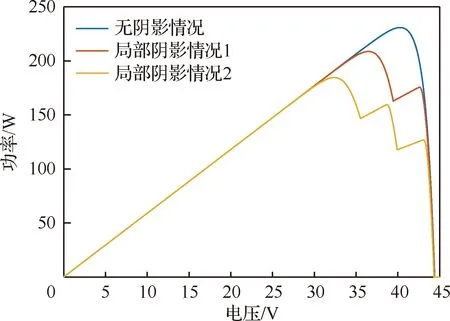
图6 局部阴影模型下太阳能电池阵列P-V特性曲线Fig.6 P-V characteristic curves of solar cell array under partial shadow model
3.1.3 飞行任务剖面
取“蒲公英I”飞行实际数据作为飞行任务剖面。飞行航迹为具有4个航点的闭环矩形航线(图7),长边为790 m,短边长度为300 m,飞行方向为逆时针按航点0-1-2-3顺序飞行。飞行高度100 m,飞行空速14 m/s。图8为飞行功率和高度变化曲线,总耗时1 070 s,包括地面滑跑(0~58 s)、等待起飞(58~282 s)、起飞爬升(282~403 s)、航点巡航(403~878 s)、下降降落(878~1 005 s)、地面滑跑(1 005~1 070 s)共6个阶段。
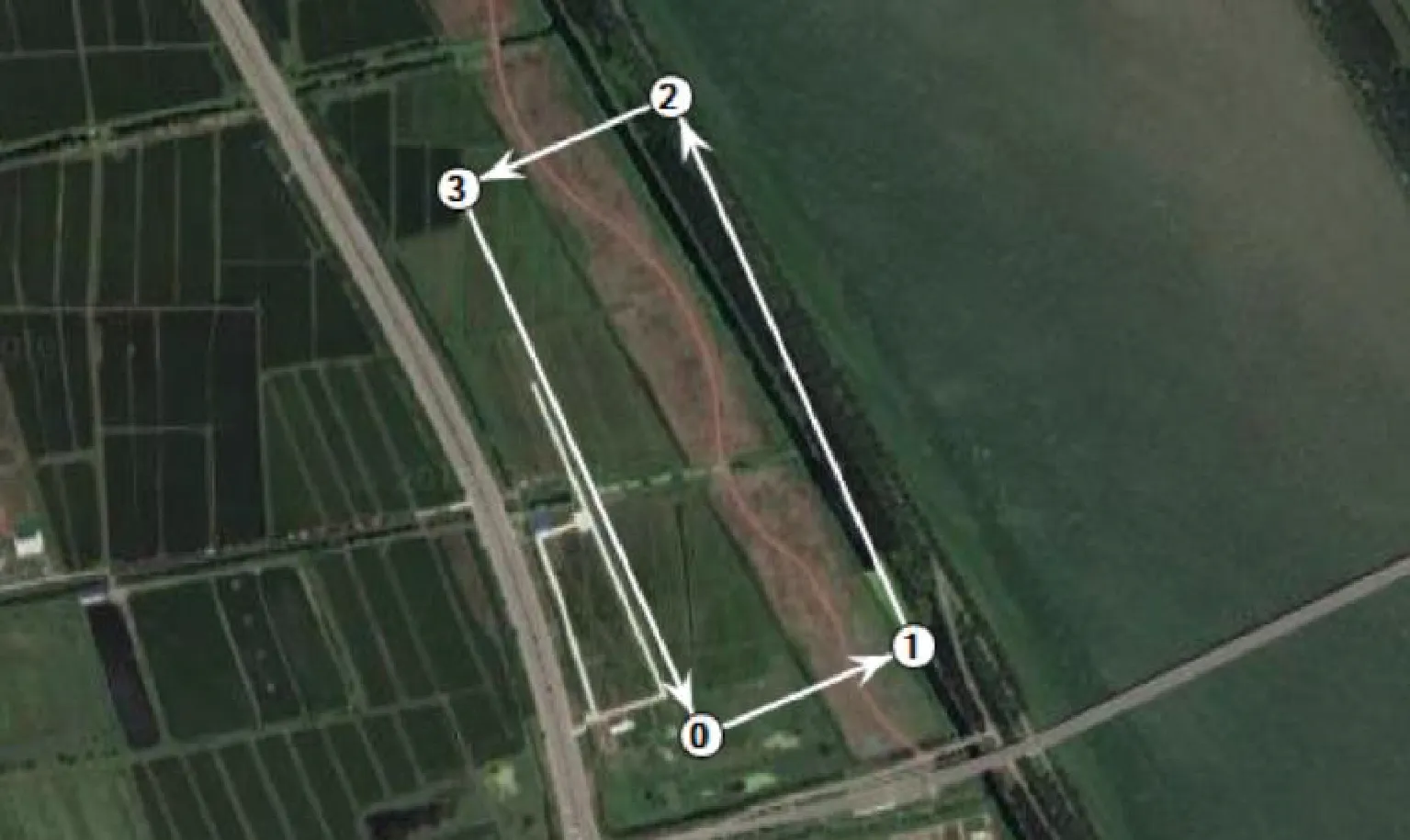
图7 “蒲公英I”飞行航线Fig.7 "Dandelion I" flight route
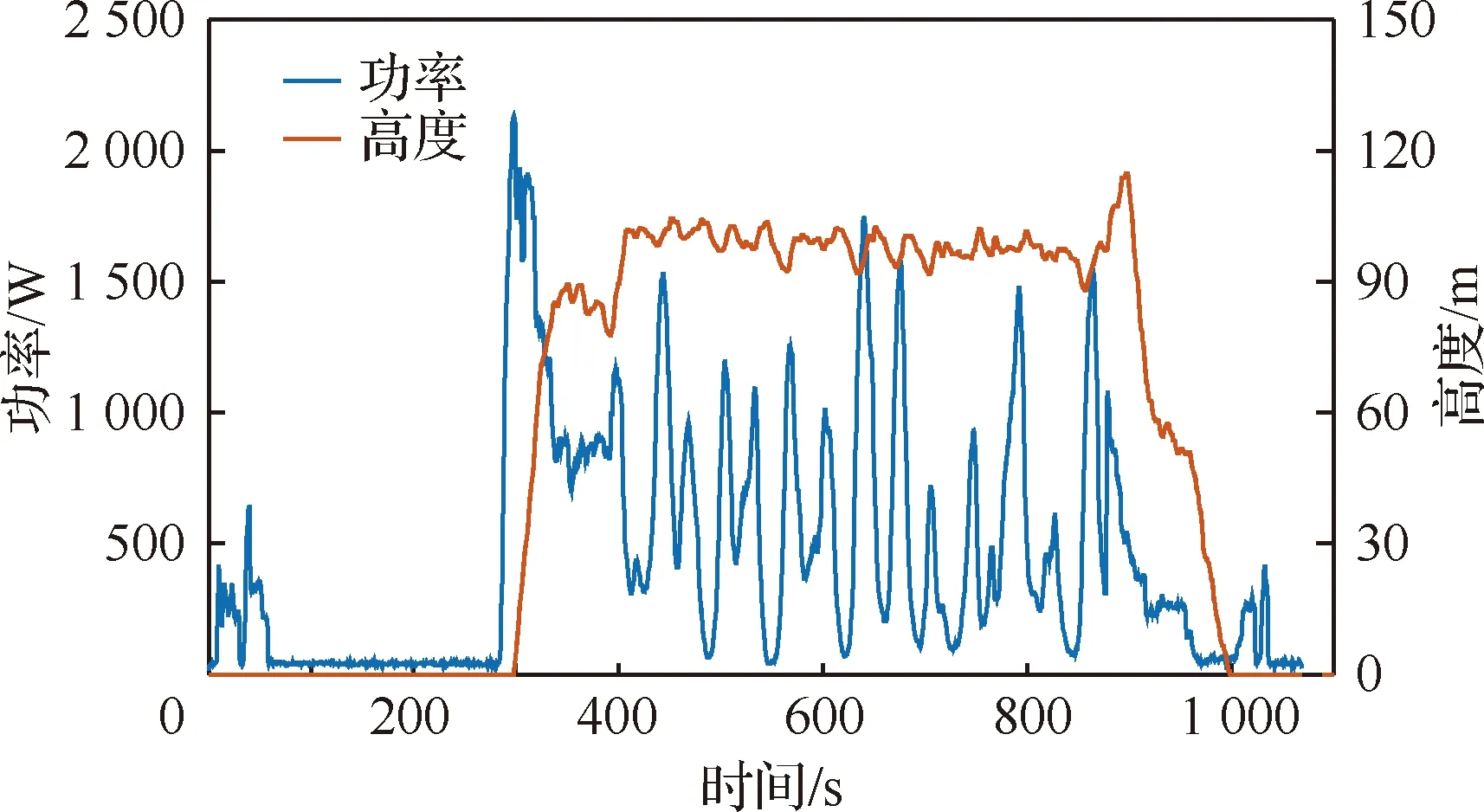
图8 飞行功率、高度-时间曲线Fig.8 Flight power, altitude-time curves
本文以图8所示功率需求曲线作为基本飞行任务剖面,在其中加入飞行过程中局部阴影情况:在转弯过程中存在表2中局部阴影情况1所示的局部阴影情况,每次转弯过程中持续15 s,存在局部阴影情况的转弯共7个。假设当天光照强度为1 000 W/m2。
3.2 最大功率点追踪仿真试验
为了对比,分别采用增量电导法(Incremental Conductance, IC)、FA和MFA进行最大功率点追踪的数学仿真和半实物仿真试验。
3.2.1 数学仿真与分析
1) 仿真模型
图9是MPPT控制系统仿真模型,主要包括:太阳能电池阵列、Buck-Boost变换电路、MPPT算法模块、DC/DC控制模块以及驱动模块。其中:DC/DC变换器输入电容为56 μF,输出电容为100 μF,负载为2 Ω纯阻性负载。DC/DC变换器控制模块中采用经典PI控制方法,搭建电压控制回路,Kp=0.014,KI=40。FA中:种群数量N=6,初始吸引度β0=1,步长因子α=0.02,光吸收系数γ=0.03;MFA中:PTH=13,θ=0.077,其余参数与FA保持一致。IC中:扰动步长为0.1 V。MPPT算法仿真步长为50 ms。
2) 稳态仿真
据调查和文献资料记载,沙沟先后于1963年、1981年和2016年暴发过泥石流,除给金山镇金狮村居民集中点和沟内居民多次造成严重的危害外,还对生态环境造成了严重的破坏。按泥石流灾害危害性等级划分表,该泥石流灾害危害性等级为大型地质灾害。
图10为太阳能电池阵列在表2中3种光照情况下的仿真功率曲线。表3为采用不同算法的最大功率点追踪仿真结果比较。可以看出:① 3种情况下,MFA和FA均能对太阳能电池阵列的最大功率点进行准确跟踪,MFA的收敛时间均小于FA,且搜索过程中的功率波动较小;② 有局部阴影情况下,IC会被困于局部最大功率点,造成功率浪费。
3) 动态仿真
将3.1.2节的动态局部阴影模型加入MPPT控制仿真系统。其中,每种光照情况持续2 s,仿真时间共10 s。图11为仿真功率曲线。可以看出:① MFA和FA都可以动态追踪全局最大功率点,与FA相比,MFA的功率波动更小、收敛时间更短;② IC在出现局部阴影情况时,被困于局部最大功率点。
3.2.2 半实物仿真结果与分析
1) 试验平台
图12为最大功率点追踪半实物仿真平台。其中,太阳能电池阵列由太阳能电池模拟器实现,作为MPPT控制系统能源;采用可编程电子负载作为MPPT控制系统负载;将MFA、FA和IC分别嵌入MPPT控制系统硬件平台,分别进行最大功率点追踪试验,对比3种算法在跟踪速度和精度方面的差别。MPPT算法执行步长仍为50 ms。
2) 稳态试验
图13为太阳能电池阵列在表2中3种光照情况下的仿真功率曲线。表4为最大功率点追踪方法的半实物仿真结果比较。可以看出:① 3种情况下,MFA和FA均能对太阳能电池阵列的最大功率点进行准确跟踪,MFA的收敛时间均小于FA,且搜索过程中的功率波动较小;② 有局部阴影情况下,IC会被困于局部最大功率点,造成功率浪费;③ 半实物仿真结果与数学仿真一致,验证了数学仿真模型的有效性。
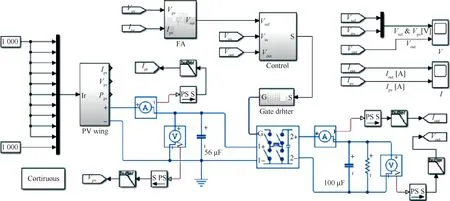
图9 MPPT控制系统仿真模型Fig.9 Simulation model for MPPT control system
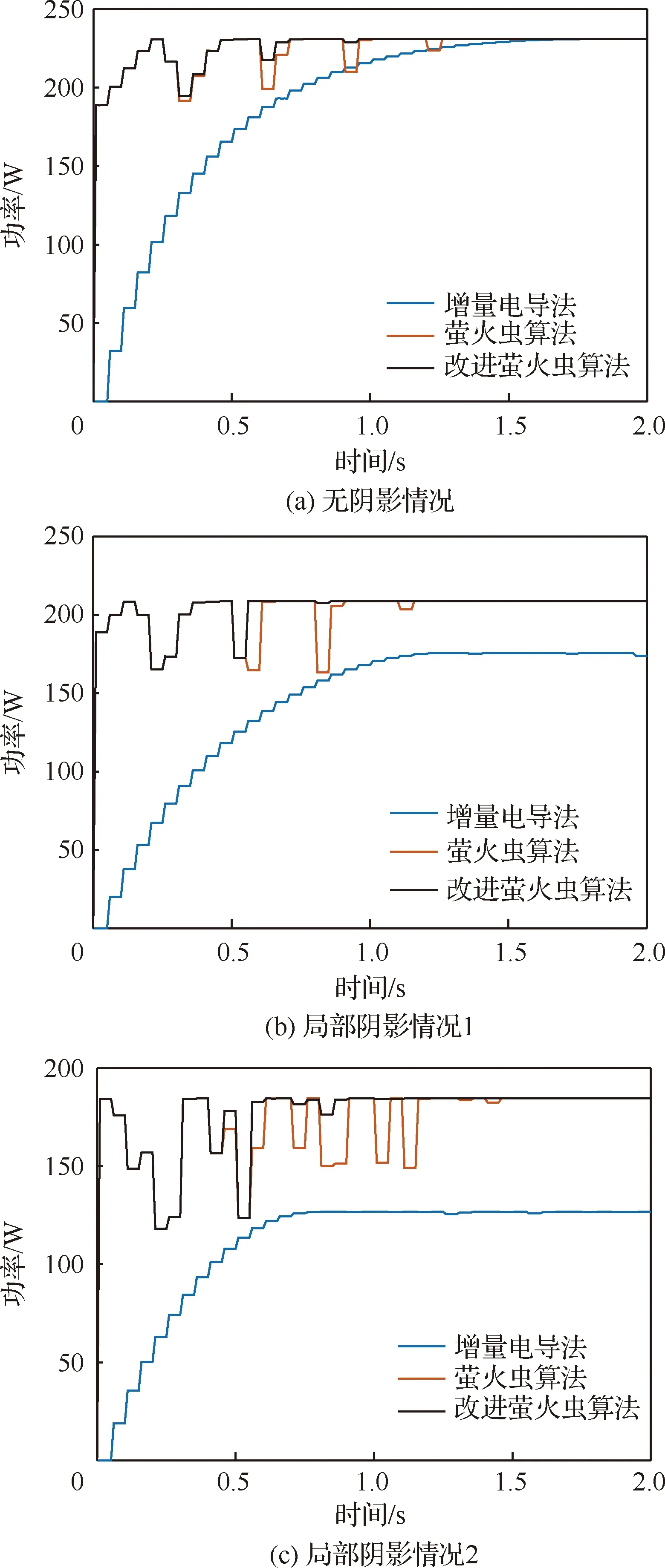
图10 最大功率点追踪稳态数学仿真功率曲线Fig.10 Maximum power point tracking static mathematical simulation power curves
表3 最大功率点追踪稳态数学仿真结果对比
Table 3 Comparison of maximum power point tracking static mathematical simulation results
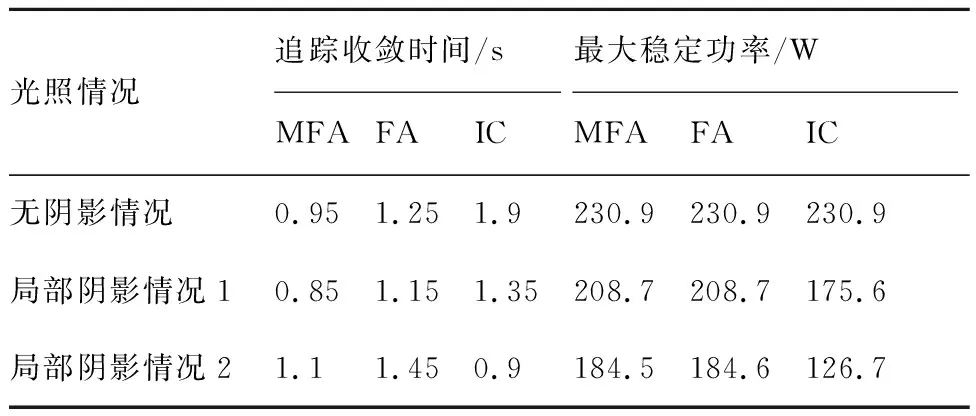
光照情况追踪收敛时间/s最大稳定功率/WMFAFAICMFAFAIC无阴影情况0.951.251.9230.9230.9230.9局部阴影情况10.851.151.35208.7208.7175.6局部阴影情况21.11.450.9184.5184.6126.7

图11 最大功率点追踪动态数学仿真功率曲线Fig.11 Maximum power point tracking dynamic mathematical simulation power curves
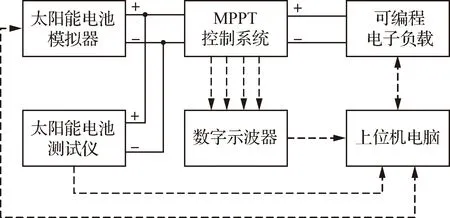
图12 最大功率点追踪试验平台Fig.12 Maximum power point tracking test platform
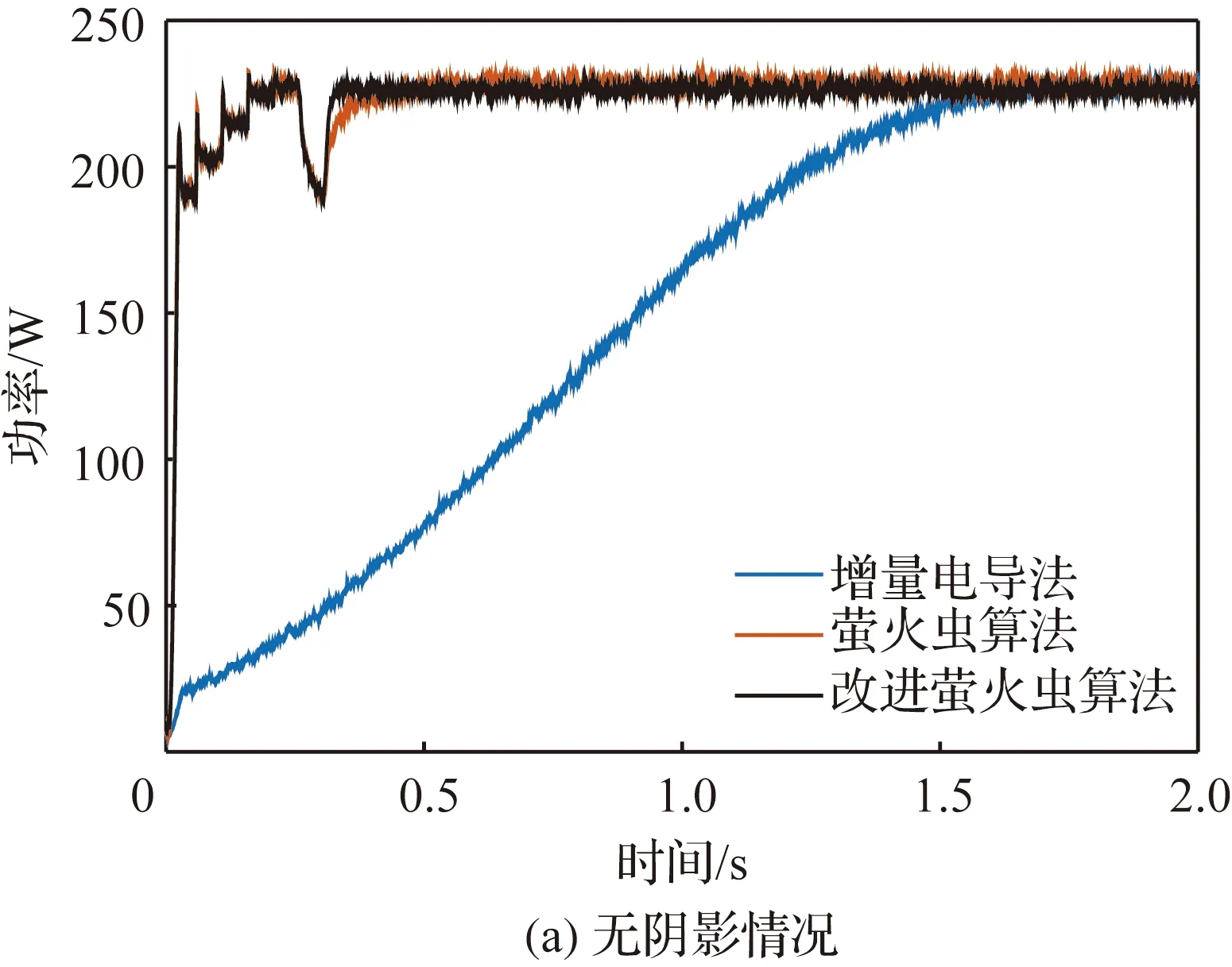
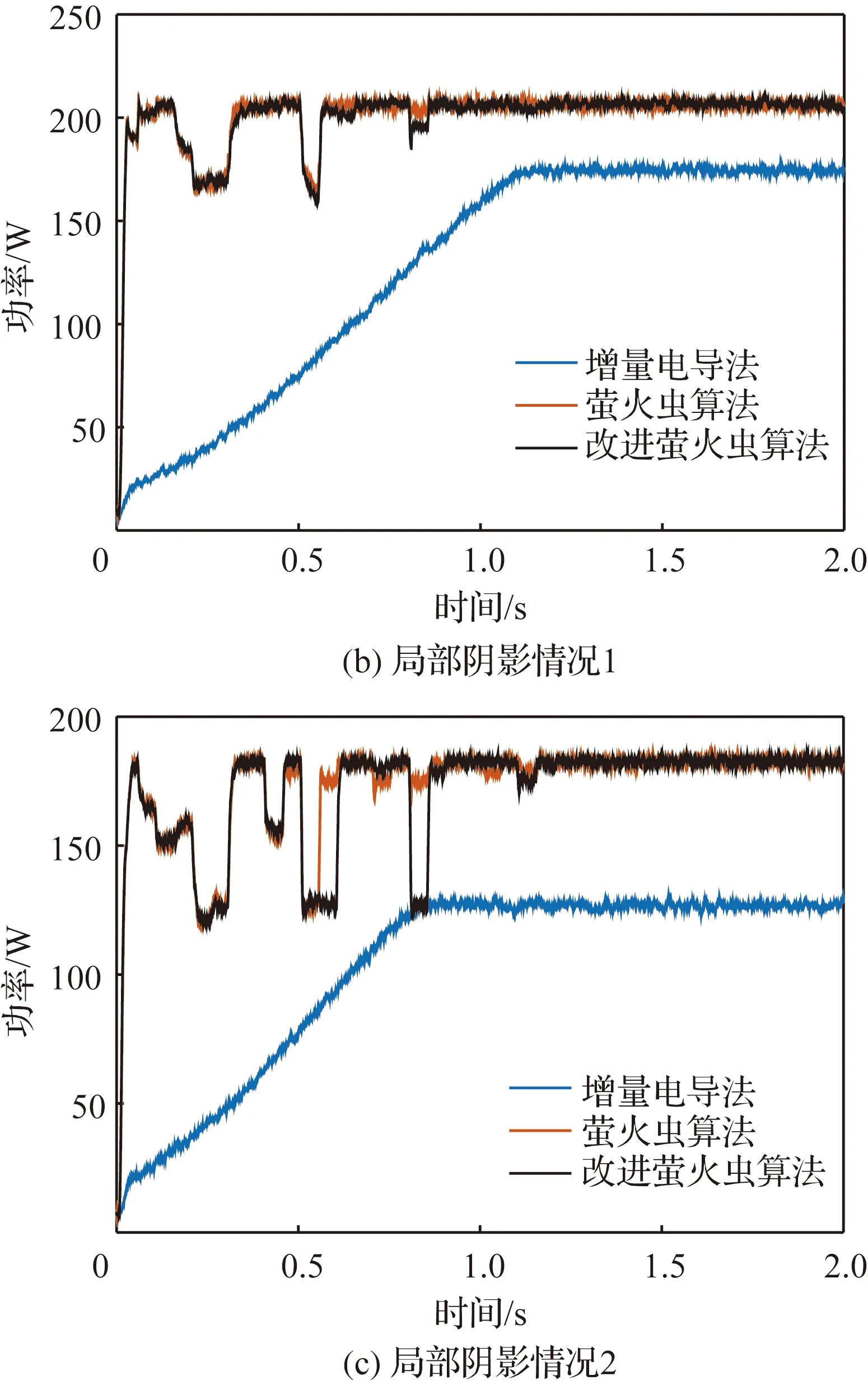
图13 最大功率点追踪稳态半实物仿真功率曲线Fig.13 Maximum power point tracking static semi- physical simulation power curves
表4 最大功率点追踪稳态半实物仿真结果对比
Table 4 Comparison of maximum power point tracking static semi-physical simulation results
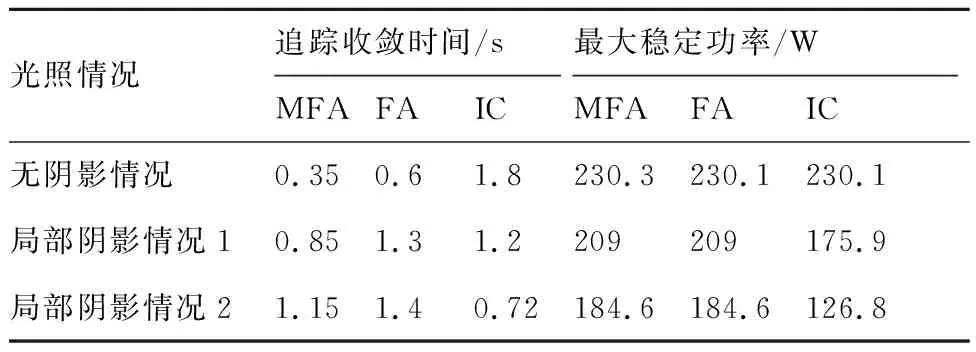
光照情况追踪收敛时间/s最大稳定功率/WMFAFAICMFAFAIC无阴影情况0.350.61.8230.3230.1230.1局部阴影情况10.851.31.2209209175.9局部阴影情况21.151.40.72184.6184.6126.8
3) 动态试验
将3.1.2节动态局部阴影模型加入半实物仿真平台,每种光照情况持续2 s,仿真时间共10 s。图14为半实物仿真功率曲线。可以看出:① MFA和FA都可以动态追踪全局最大功率点,与FA相比,MFA的功率波动更小、收敛时间更短;② IC在出现局部阴影情况时,被困于局部最大功率点;③ 与数学仿真结果一致。
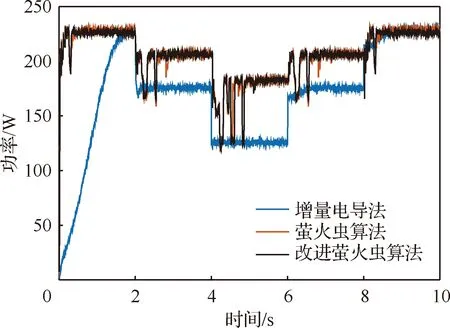
图14 最大功率点追踪动态半实物仿真功率曲线Fig.14 Maximum power point tracking dynamic semi-physical simulation power curves
3.3 混合能源控制仿真试验与分析
“蒲公英I”无人机采用左右对称的双能源动力系统架构,本文以其右侧混合能源动力系统为原型,基于3.2.1节MPPT仿真模型,加入飞行任务剖面需求功率,建立混合能源管理系统仿真模型,如图15所示。本文采用容量为2.6 Ah的6S锂聚合物电池,参数取值如表5所示。
在典型飞行任务剖面下,采用第1节给出的MFA和第2节给出的能源管理策略,对能源管理策略功率分配和能源状态进行仿真。仿真中设置蓄电池初始电量为80%,结果如图16所示。可以看出:① 当需求功率高于太阳能电池最大功率时,太阳能电池以最大功率输出,其余功率由蓄电池补充;② 均匀辐照情况下MFA能够迅速搜索到最大功率点并维持输出。当出现局部阴影情况时,MFA检测到功率波动,重新开始搜索最大功率点,经短暂的功率波动后稳定在全局最大功率点输出;③ 当系统剩余功率高于蓄电池最大充电功率时,限制充电功率为最大充电功率以保护蓄电池;④ 蓄电池电压跟随负载变化在24.15~24.83 V范围内波动,蓄电池电流波动范围为-4.65~34.5 A,电压电流均处于正常区间内,未发生过充过放现象,蓄电池始终处于正常状态健康运行。
为分析本文所提能源管理策略的适应性,保持典型任务剖面不变,在不同蓄电池初始电量(95%、80%、40%)情况下进行仿真研究,结果如图17所示。
可以看出:① 在较高的初始电量状态(95%)下,蓄电池仅放电不充电;② 当蓄电池初始电量处于中低状态(80%和60%)时,在无人机待机过程中SOC曲线存在明显的上升即充电过程;③ 在无人机飞行过程中,不同初始电量的SOC曲线随需求功率波动,具有较好的一致性。表明本文设计的状态机能源管理策略在不同初始电量状态下能够有效管理混合能源系统的功率流,在充分利用太阳能功率的同时保持蓄电池处于健康运行状态,具有较强的适应性。
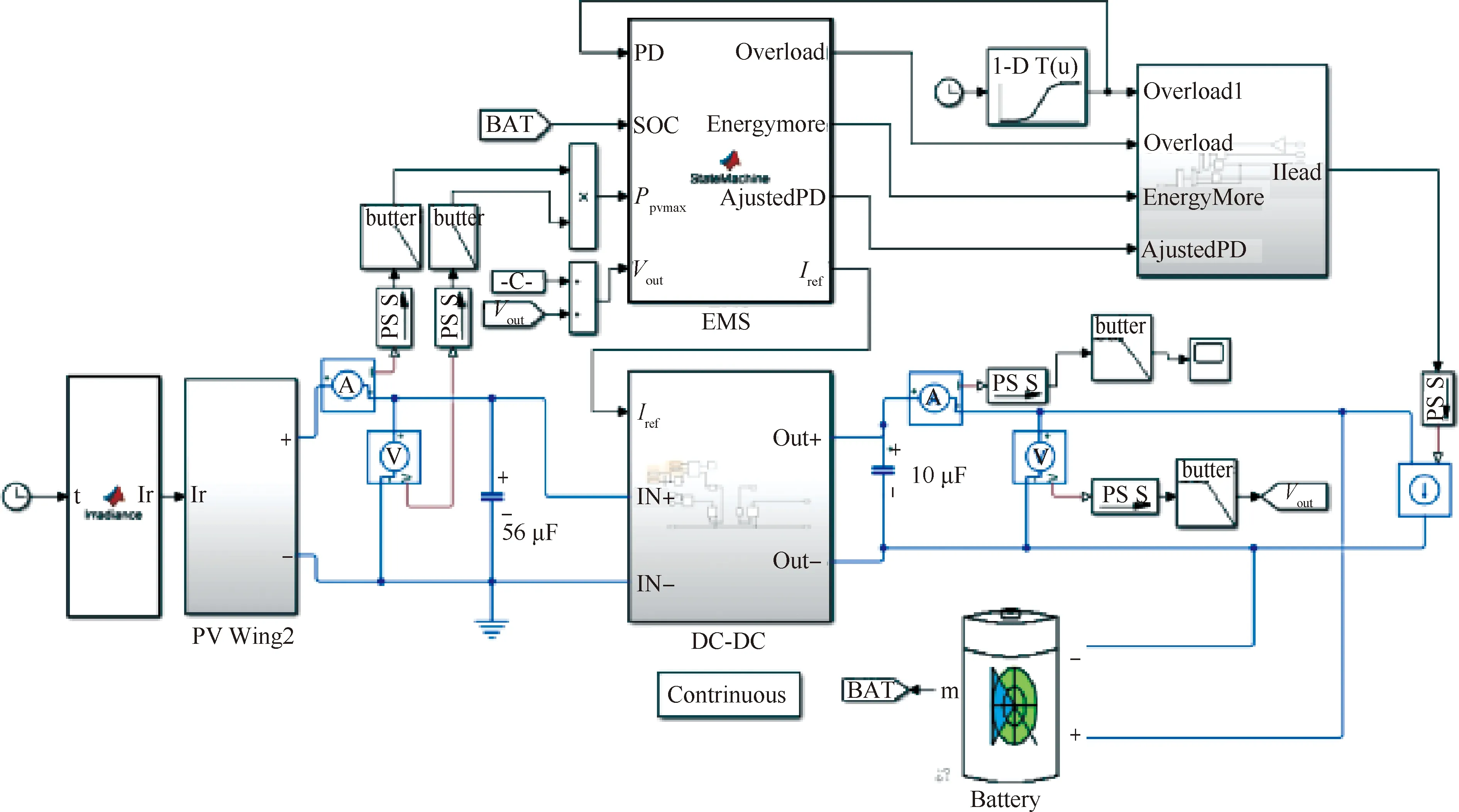
图15 混合能源管理策略仿真模型Fig.15 Hybrid energy management strategy simulation model
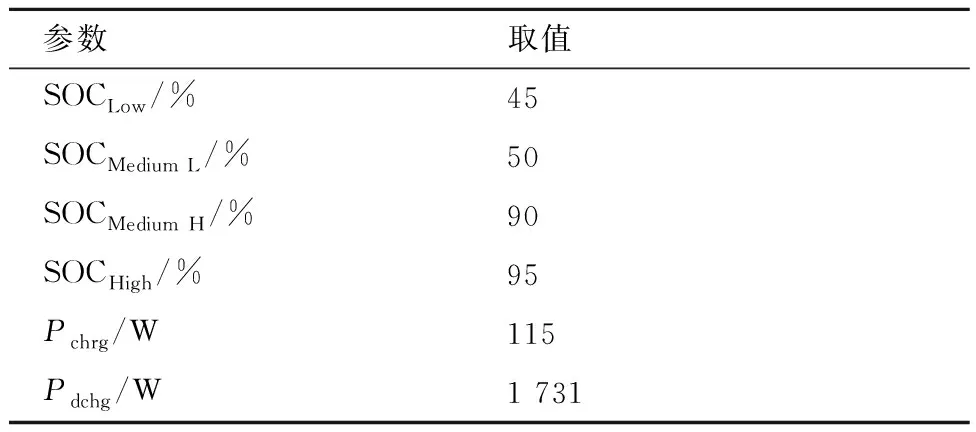
表5 蓄电池参数取值Table 5 Lithium battery parameter values
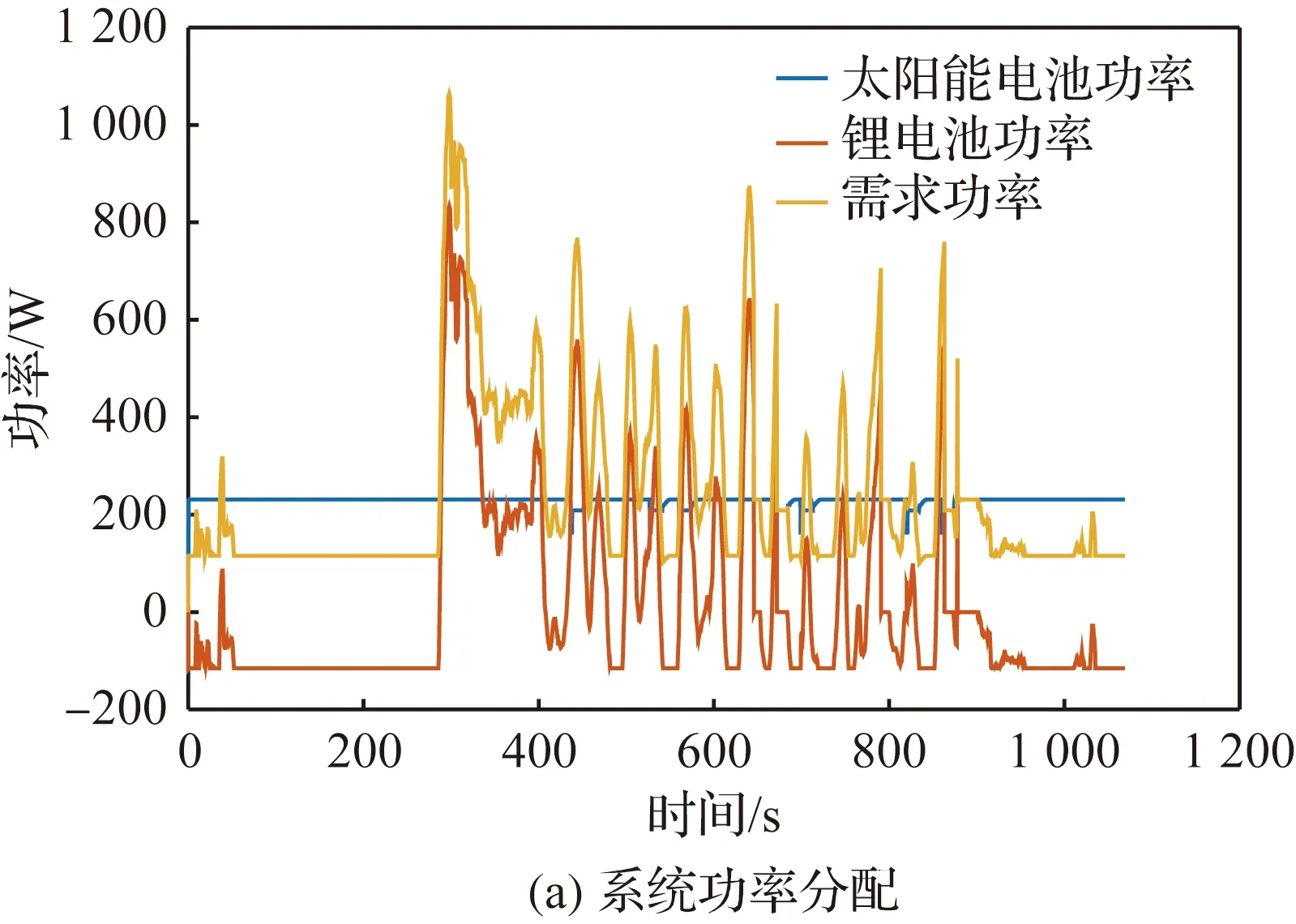
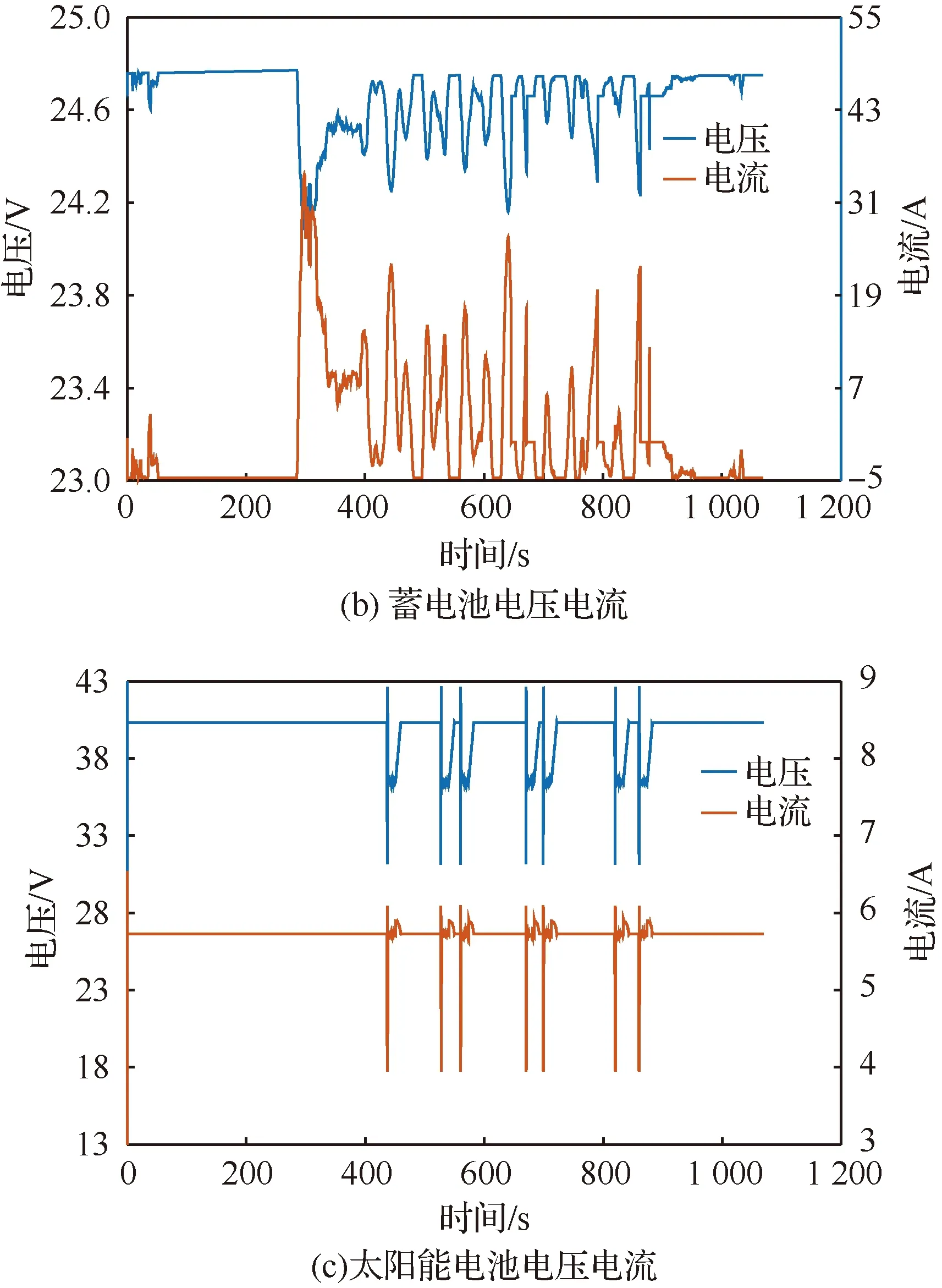
图16 功率分配和能源状态Fig.16 Power distribution and energy status
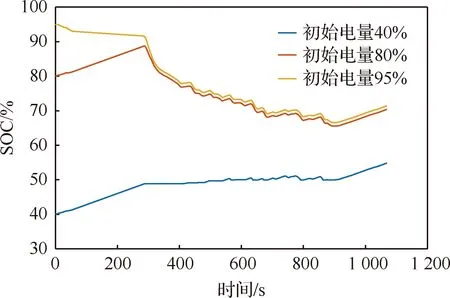
图17 不同初始电量情况SOC变化曲线Fig.17 SOC curves of different initial power conditions
4 结 论
本文针对太阳能无人机太阳能电池局部阴影问题,对太阳能电池全局最大功率点追踪算法和混合能源管理展开了深入的研究,所得结论如下:
1) 所提改进萤火虫算法与萤火虫算法相比,收敛时间明显提高。
2) 基于改进萤火虫的算法MPPT方法在不同光照情况下均能实现全局最大功率点的准确跟踪,且功率波动小。
3) 对于含有局部阴影的飞行剖面,提出的改进萤火虫算法和所设计的混合能源控制规则,可以有效实现太阳能电池和蓄电池的功率分配,且蓄电池电量变化处于合理范围。

