一种基于LSTM模型的日销售额预测方法

吴娟娟，任 帅，张卫钢，伍 菁，李香云

(长安大学 信息工程学院，陕西 西安 710064)

0 引 言

零售商店日销售额预测是从已有的日销售额资料中总结出商品的日销售额规律，并且用此规律动态预测未来一段时间内的日销售额，从而指导未来的销售方法或手段，提高销量，获取更大利润。日销售额的分析是一个复杂且不规则的非线性系统。重点分析并且找到影响商品销售额的一些主要因素。但由于新产品的开发、季节性变换、促销活动、节假日、天气及政策的变化等各种原因，传统分析方法的准确性在一定程度上受到很大质疑。因此，希望建立一个非线性系统，其参数可以随预测环境的变化而变化，从而克服该缺点。

为了得到更精准的预测结果，许多学者根据市场的调研和研究，运用多种方法针对已有的数据进行分析和对比[1]。比如：Xgboost单模型[2]、指数平滑法、ARIMA模型和GARCH模型等[3-4]。但是Xgboost单模型采用预排序，在迭代之前，对节点的特征做预排序，遍历选择最优分割点，数据量大时，贪心法耗时，数据分割的复杂度高；指数平滑法精确率不高；ARIMA模型对于趋势性较强的数据集预测效果比较好，但如果遇到趋势不那么强的数据集，则效果不太理想；对于非对称现象，GARCH模型无法解释该现象，为了保证其非负性，假设模型表达式中的全部系数都大于零，这些约束中所隐含的任何一个滞后项的增大将会增加因而排除了的随机波动行为，导致在估计该模型时有可能会出现震荡现象；LSTM模型[5]避免了长期依赖问题，采用特殊隐式单元，在继承了大部分RNN模型特性的同时解决了梯度反传过程中[6]由于逐步缩减而产生的Vanishing Gradient问题[7]，适用于非线性回归变量，可以解决多个输入变量的问题，模型准确度高，训练速度快，并行处理能力强。LSTM更适合用于处理与短期时间序列高度相关的问题，在n个示例批次中不断迭代，能够快速和准确地对大量短期时间序列数据进行处理，是解决时间序列预测问题最常用的工具。

针对大数量级的序列预测，文中建立了一种Tensorflow框架下基于记忆机理的LSTM模型。以预测值和实际值的误差为优化目标，从网络结构的搭建，学习率、窗口设置上改进网络模型预测的准确性，采用RMSProps算法修正模型自适应率。最后，应用销售额数据进行验证，并与传统时间序列预测模型进行对比，实验结果表明建立的LSTM模型在销售额预测上具有良好的优越性。

1 LSTM神经网络

LSTM是一种改进的RNN，比一般的RNN能够记住更长周期上的信息模式，在解决很多问题上都取得了成功，例如自然语言处理、中文文本分类研究、机器翻译等。

目前为止，实际应用中最有效的序列模型为门控RNN(gate RNN)，包括基于长短期记忆网络(long short-term memory)和基于门控循环单元(gate recurrent unit)的网络。LSTM网络比一般的RNN结构更适于长期依赖，在序列处理问题上获得很好的表现[8]。LSTM结构如图1所示。

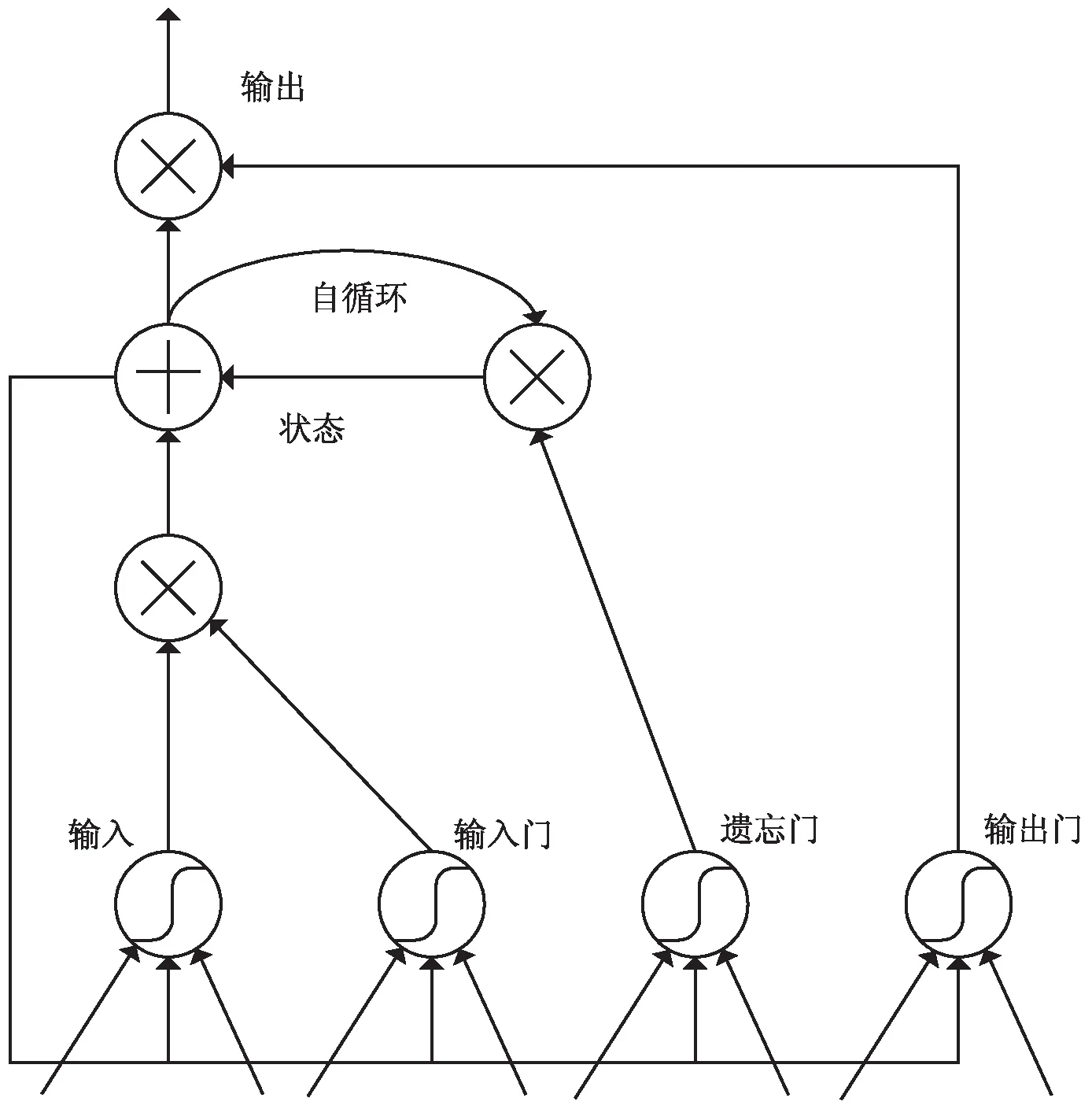
图1 LSTM结构

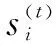
Input gates：

(1)

Forget gates:

(2)

Cells：

(3)

(4)

Output gates：

Cell outputs：

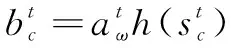
(6)

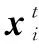
(7)

Cell outputs：

(8)

Output gates：

(9)

States：

(10)

Cells：

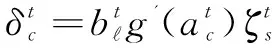
(11)

Forget gates：

(12)

Input gates：

(13)

式(8)中g和前向传播中的h含义相同，即泛指，由于它不一定只能输出到下一个时间的自身，或许还会输出到下一个时间其他的隐层。

2 LSTM优化算法

大多数深度学习算法通常以最小化代价函数、损失函数(loss)或误差函数J(θ)作为优化目标。J(θ)用来描述预测值和真实值的偏离程度，文中指的是均方根值。优化可以分成两个阶段，第一阶段是使用前向传播算法计算得到预测值，再将预测值与真实值比较得到它们之间的差距；第二阶段使用反向传播算法，计算出损失函数对所有参数的梯度，然后按照梯度和学习率(learning rate)利用梯度下降法(gradient decent)更新每一个参数。假设θ表示神经网络参数，优化过程可看作迭代更新并寻找一个参数θ，使得J(θ)最小。

梯度下降的计算过程指沿着梯度下降的方向求解极小值，迭代公式为：

x*=argminf(x)

(14)

梯度下降的计算过程指沿着梯度下降的方向求解极小值，迭代公式为：

xt+1=xt+ηg

(15)

其中，g表示梯度负方向，η表示梯度方向上的搜索步长，在LSTM中表示为学习率。学习率太大容易导致发散，太小收敛速度太慢，对模型精度起着至关重要的作用。

梯度下降法要在全部训练数据上最小化损失，当样本容量非常大或是迭代次数加大时会非常消耗计算资源。随机梯度下降(stochastic gradient descent，SGD)优化损失函数，按照数据生成分布抽取m个小批量(独立同分布的)样本，每一次迭代只计算一个样本的loss，然后再遍历所有的小批量样本，进行一轮完整的计算。再计算其梯度的均值，最后获得梯度的无偏估计，更新如下所示：

随机梯度下降算法在第k个训练迭代的更新方法

输入参数：学习率η

输入参数：初始参数θ

While 满足do，则停止

从训练数据集中采集m个小批量样本{x(1),x(2),…,x(m)}，xt对应输出目标yt

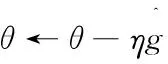
End while

SGD算法中关键的参数是学习率，在LSTM应用中会随着时间的推移逐渐改变学习率。

2.1 自适应学习率算法

学习率对模型的性能有显著的影响，决定了参数移动到最优值的速度。若幅度过大，会导致参数可能越过最优值；幅度过小，容易引起运算冗余，导致长时间运算无法收敛。目前常用的学习率算法有AdaGrad[9]、RMSProp[10]、Adam[11]等。Schaul[12]展示了许多算法在大量学习任务上极具价值的比较。有结果表明，RMSProp和AdaDelta算法表现都相当良好。文中使用如下方法改变学习率：

RMSProp算法

输入参数:全局学习率η，衰减速率ρ

输入参数:初始化参数θ，初始化累积变量γ=0

While满足do，则停止

从训练数据集中采集m个小批量样本{x(1),x(2),…,x(m)}，xt对应输出目标yt

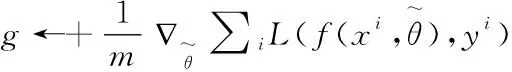
累积梯度：γ=ργ+(1-ρ)g⊙g

应用更新：θ←θ+Δθ

End while

RMSprop是一种自适应学习率方法，通过自动调整学习率，从而改变更新方式。

2.2 超参数选择

深度学习算法中使用超参数来控制计算，选择超参数有两种方法：手动选择和自动选择。手动选择超参数的主要目标是调整模型的有效容量以匹配任务的复杂性。但手动选择需要了解超参数、泛化误差、训练误差和计算环境等问题，高度依赖平台。自动选择超参数算法不需要制定学习算法的超参数，常见的有网格搜索、随机搜索。

LSTM预测模型中包含很多参数，其中以学习率、分割窗口、状态向量大小最为关键。将这些超参数笛卡尔乘积得到一组超级参数。Bernoulli and Bengio[13]对比了网格搜索和随机搜索，发现随机搜索能更快地减小验证误差。

3 实 验

3.1 实验流程

文中采用基于TensorFlow[14-15]的LSTM模型的零售商店日销售额预测方法，建立的预测模型可以预测某大型连锁零售商店未来7天的日销售额，预测的基本步骤如图2所示。

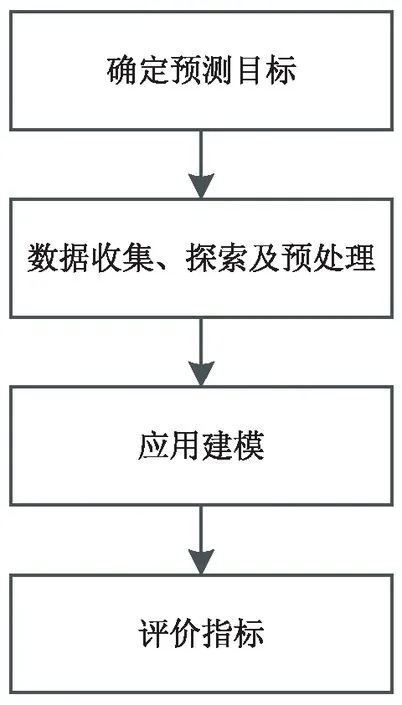
图2 基本步骤

(1)确定预测目标。

根据相关业务背景分析原始数据源，预测未来7天的日销售额情况。

(2)数据收集、探索及预处理。

实验使用的数据是某大型连锁零售商店在2018年1月1日至2018年6月30日的销售数据(数据有缺失)，共267家店，每家店181条数据。分析各个因素与销售额的关系，找出影响因变量的自变量，包括内部数据、外部数据以及额外数据。由于原始数据源并非完整的数据源，其中会出现缺省值或者异常值这些噪声数据，所以需要对缺省值和异常值进行处理，补全有效数据源，然后对数据进行离散化、归一化处理。以1000011店为例，处理得到的部分数据如表1所示。

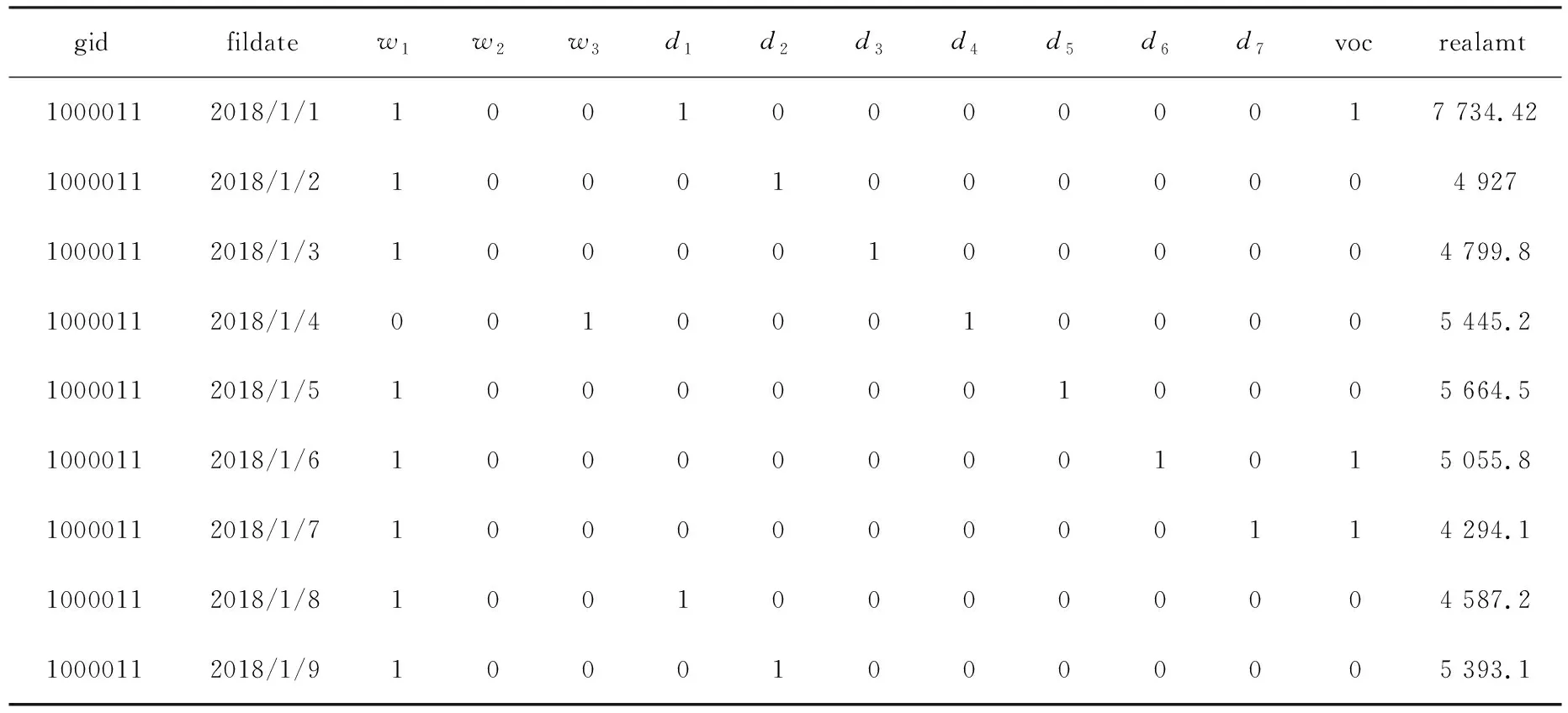
表1 销售额数据

其中，gid表示商店ID，共267家(181条数据)；fildate表示销售时间；d(dayofweek)表示当天处于周几；voc表示国家法定节假日；w(weather)表示天气(100-晴，010-雨，001-雪)。

文中利用天气、处在周几以及是否为节假日等特征因素来分析对销售额的影响，根据特征建立模型实现对销售额的预测。

(3)应用建模。

首先，将数据集划分为训练集和测试集；其次，对于训练集做特征筛选，提取有信息量的特征变量，并且去掉无信息量等的干扰特征变量；最后，应用算法建立LSTM模型后，结合测试集对算法模型的输出参数进行优化，提高泛化能力，从而提高预测精度，得到最终的训练模型。

(4)评价指标。

预测回归类模型精度常用的评价方法[16]有RMSE(root mean squared error，均方根误差)、MAPE(mean absolute percentage error，平均绝对百分比误差)、MAE(mean absolute error，MAE)和MPE(mean percentage error，平均百分比误差)。文中将选取MAPE和MAE作为衡量标准，MAPE的大小用来衡量一个模型预测结果的好坏，MAPE的值越小，则模型的预测结果越好，MAE的值更好地反映了预测值误差的实际情况，MAE的值越小，模型预测的误差越小。

3.2 实验结果分析

分别采用LSTM和Xgboost对1001281店2018年6月24日—2018年6月30日的每日销售额进行预测，LSTM和Xgboost的预测结果如图3所示。文中采用绝对百分误差[17]和平均绝对误差[18]作为最终算法质量的衡量标准，MAPE和MAE越低则表明算法误差越小，公式如下：

(16)

(17)

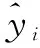
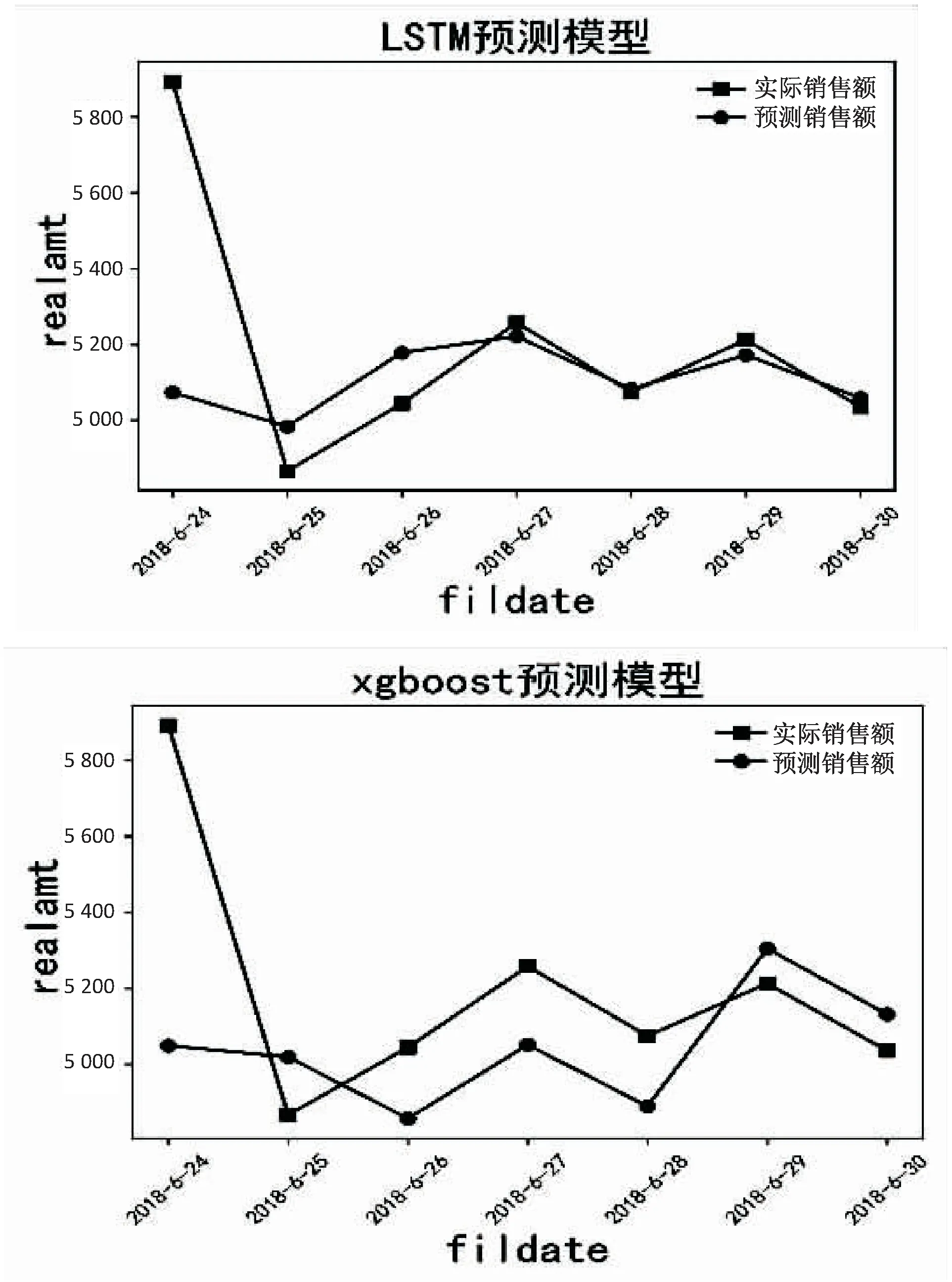
图3 LSTM、Xgboost一周日销售额预测结果

LSTM和Xgboost零售商店日销售额预测模型的预测性能指标如表2所示。

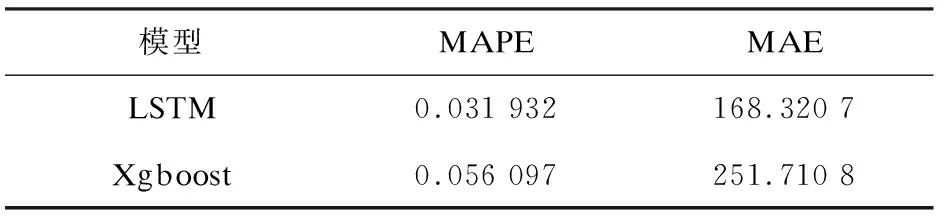
表2 两种方法的预测性能指标

可见，无论是MAPE还是MAE，LSTM模型的预测效果都稍优于Xgboost。

4 结束语

文中基于TensorFlow框架建立了LSTM模型并预测了商品销售额，然后与Xgboost模型的预测结果进行了比较。在保证参数调优的情况下，根据MAPE和MAE评价标准，对比二者的预测结果，发现LSTM模型的MAPE为0.031 932，MAE为168.320 7，而Xgboost模型的MAPE为0.056 097，MAE为251.710 8。结果表明，LSTM模型的准确性更好，用其预测商品的销售额是可行的。该方法具有较高的实用价值。但实际商品销售往往受到政治、经济、文化等多种因素的影响，用该方法预测仍存在不足，如何对各种因素进行取舍，将是今后努力的方向。