基于小样本SVR的迁移学习及其应用
易 未,郑沫利,赵艳轲,毛 力,孙 俊
(1.江南大学 物联网工程学院,江苏 无锡 214122;2.国贸工程设计院,北京 100037)
0 引 言
数据挖掘与机器学习技术在许多知识工程(例如分类、回归和聚类)等领域取得了有意义的成就[1]。但是,很多机器学习算法只有在训练集与测试集数据来源于单一场景、具有相同的特征空间和数据分布以及样本数量充足时,才能取得让人满意的实验结果。特别地,当样本数量不足时,容易出现过拟合现象,会显著地降低学习算法的效果[2]。然而在现实生活中,得到目标场景中的大量样本数据是很困难的,例如待观测的目标本身数量较少且不支持多次观测;或者是观测一次成本过高,只能使用现有的少量数据。
加权ε支持向量回归(ε-WSVR)算法具有扎实的理论基础和较好的泛化能力,应用在众多领域[3-5]。该算法为不同的样本设置不同的权值,给予样本不同的精度要求和偏离精度要求的惩罚参数,减轻标准支持向量机对孤立点或噪声数据的敏感性,抑制过拟合现象的产生。
Bagging算法通过对目标数据集进行数次有放回地抽样,形成多个不同的子数据集。然后在各个子数据集上使用基学习器,再将这些基学习器进行结合。对于分类任务采用简单投票法,对回归任务采用简单平均法,产生一个具有较强泛化能力的模型[6]。
迁移学习技术把目标任务称为目标域(target),与目标任务相关联的其他任务称为源域(domain),通过使用源域的数据或者知识来辅助建立目标域模型,提高模型的泛化能力[7]。针对分类任务,目前已经提出了很多基于迁移学习的研究成果,例如Dai等人借用AdaBoosting算法的思想提出了TrAdaBoosting算法,将源域中适合目标域模型训练的样本权重增加、其他样本权重减少[8];Liu等人借用Bagging算法的思想提出了BETL算法,在自助采样后的子数据集上训练的初始分类器对未标示数据进行标示,然后用扩充了的标示数据训练未标示数据[9];Lin等人提出Double-bootstrapping算法,在训练集上使用自助采样之后又再测试集上使用自助采样,两次自助采样提升模型分类精度[10]。针对回归任务,史荧中等人使用支持向量回归机(SVR)在历史数据和目标数据上构建两个尽可能相似的回归超平面,但该方法一旦运用到源域数据不为目标域的历史数据场景时,会给生成模型带来一定干扰[11];Yu等人提出了改进的RMTL算法,使用SVR在源域与目标域数据上建立两个回归超平面模型,组合使用这两个模型提升泛化能力[12]。
但以上研究并没有对小样本(样本数小于30)情况下的迁移回归进行研究。文中针对小样本数据情况下的回归系统建模问题,提出了一种小样本数据的迁移学习支持向量回归机方法,以加权ε支持向量回归机为Bagging算法的基学习器,使用与目标任务相关联的源域数据来弥补当前场景数据不足的问题。实验证明,该方法减少了回归误差,提高了目标模型的泛化能力。
1 相关知识
1.1 加权ε支持向量回归(ε-WSVR)算法
对于ε支持向量回归(ε-SVR)算法来说,设给定的训练样本集合为D={(x1,y1),…,(xi,yj),…,(xm,ym)},xi∈RN,yi∈R,ε-SVR算法的基本思想是得到一个形如式(1)的回归模型:
f(x)=ωT·Φ(x)+b
(1)
其中,ω与b是模型的参数,Φ是一个非线性映射,将有限维x映射到一个高维特征空间使训练样本线性可分,Φ(x)为将x映射后的特征向量。可以使用适当的核函数κ(xi,xj),使xi与xj在高维特征空间的内积等于其在原始样本空间上内积的结果。
传统回归模型通常当且仅当模型的输出f(x)与真实值y相等时,损失才为零,但是ε-SVR仅当|f(x)-y|<ε时,损失才为零。于是ε-SVR可形式化为式(2):
(2)
约束条件为:
f(xi)-yi≤ε+ξi
(3)
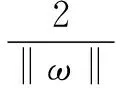
加权ε支持向量回归(ε-WSVR)算法[13]在式(2)的基础上添加权值μ,得到式(4):
(4)
式(4)可以使用SMO(sequential minimal optimization)算法求解,算法的时间复杂度为Ο(n2.3)[14]。
1.1 ε-WSVR算法权值的确定
源域中的样本数据与目标域中的样本数据越相似,则辅助建立的目标域模型泛化能力越好[8]。文中使用样本间的标准化欧氏距离来定义样本数据的相似情况,则ε-WSVR算法权值μ按照式(5)来计算:
(5)
其中,l为源域中样本xi到目标域中样本标准化欧氏距离的列向量,min(l)为该列向量中的距离最小值。所以权值μ的取值范围是(0,1]。
1.3 改进的RMTL算法
设源域样本集合为s,目标域样本集合为t,改进的RMTL问题可形式化为:
(6)
约束条件为:
fs(xs,i)-ys,i≤εs+ξs,i
ft(xt,i)-yt,i≤εt+ξt,i
(7)
其中λ>0为常数,当λ较大时,将会导致源域与目标域的回归向量ω相似;当λ较小时,将会导致源域与目标域的回归向量ω不同。
求解式(6)与式(7)的对偶问题,可得该算法模型为:
(8)
2 小样本数据的迁移学习支持向量回归算法
2.1 算法的基本思想
小样本数据的迁移学习支持向量回归算法的主要思想是将ε-WSVR算法作为Bagging算法的基学习器,使用自助采样(bootstrap)方法从源域和目标域数据集中进行采样,得到一系列子数据集。然后计算子数据集各个样本到目标域数据集中的标准化欧氏距离,得到子数据集到目标域数据集的最小距离,并把这个距离加一的倒数作为ε-WSVR算法的权值。最后使用这一系列子学习器对测试数据进行计算,把子学习器结果的简单平均值作为小样本数据的迁移学习支持向量回归算法的结果。
2.2 算法流程
输入:源域数据集source,目标域数据集target,Bagging算法的基学习器个数T,ε-WSVR算法ζ。
过程:
1:fort=1,2,…,Tdo
2:C=standardizedEuclideanDist(Dbs,target)
Dbs是source与target上自助采样产生的样本集合
3:C'=min(C)
C'是Dbs到target数据集距离的最小值
4:ht=ζ(Dbs,target,C')
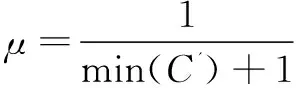
5:end forhi
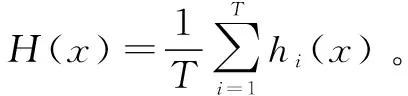
2.3 算法的时间复杂度分析
假设source数据集大小为n,target数据集大小为m。Bagging算法的基学习器ε-WSVR算法的复杂度为O((m+n)2.3),自助采样过程的复杂度为O(m+n),计算到target数据集距离复杂度为O(mn),计算权值复杂度为O(m+n)。小样本数据的迁移学习支持向量回归算法的复杂度为T*(2*O(m+n)+O(mn)+O((m+n)2.3)),考虑到T通常是一个不太大的常数,因此,小样本数据的迁移学习支持向量回归算法的时间复杂度为O((m+n)2.3),与直接使用ε-WSVR算法的复杂度同阶。
3 实 验
文中实验将使用辽宁、陕西、山西、安徽、江苏、湖北、湖南、四川和广东一共九个省份的大米与玉米储藏环节损失情况调查数据,以及三个UCI Machine Learning Repository数据集(分别是Wine Quality、Student Performance、PM2.5 Data of Five Chinese Cities)对提出的小样本数据的迁移学习支持向量回归算法进行实验,其中将四个目标域数据集按照2∶1的比例划分为训练集与测试集。将分别构建以下回归模型进行对比:(1)只使用目标域数据和标准ε-SVR算法建立的回归模型(SVR-t);(2)利用源域数据和目标域数据与标准ε-SVR算法建立的回归模型(SVR-s,t);(3)使用改进的RMTL算法基于源域数据和目标域数据建立的回归模型(RMTL-s,t);(4)使用文中方法基于源域数据和目标域数据建立的回归模型(bagg-WSVR)。以上四种回归模型采用式(9)均方误差[15]进行比较:
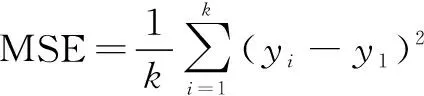
(9)

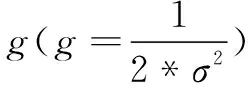
实验环境:实验硬件为Intel Core i5-2430M CPU,主频2.40 GHz,内存8 GB,编程环境为Matlab R2016b与MyEclipse2015。
3.1 四个数据集描述
Wine Quality数据集使用白葡萄酒当作源域数据集,从红葡萄酒数据集中随机选择30条样本数据作为目标域数据集,quality属性作为输出变量;Student Performance数据集使用GP学校的Math当作源域数据集,从MS学校的Math数据集中随机选择30条样本数据作为目标域数据集,G1、G2与G3属性的数值之和作为输出变量;PM2.5 Data of Five Chinese Cities数据集使用北京2014年8月删除时间属性当作源域数据集,从沈阳2014年8月删除时间属性数据集中随机选择30条样本数据作为目标域数据集,PM_USPost属性作为输出变量;粮食储藏数据集使用大米数据当作源域数据集,玉米数据作为目标域数据集,储藏环节损失率作为输出变量。四个数据集描述如表1所示。

表1 四个数据集描述
3.2 四个数据集上各个模型的回归结果与分析
wine数据集上各个模型的性能比较如表2所示。
student数据集上各个模型的性能比较如表3所示,
pm2.5数据集上各个模型的性能比较如表4所示。
粮食储藏数据集上各个模型的性能比较如表5所示。
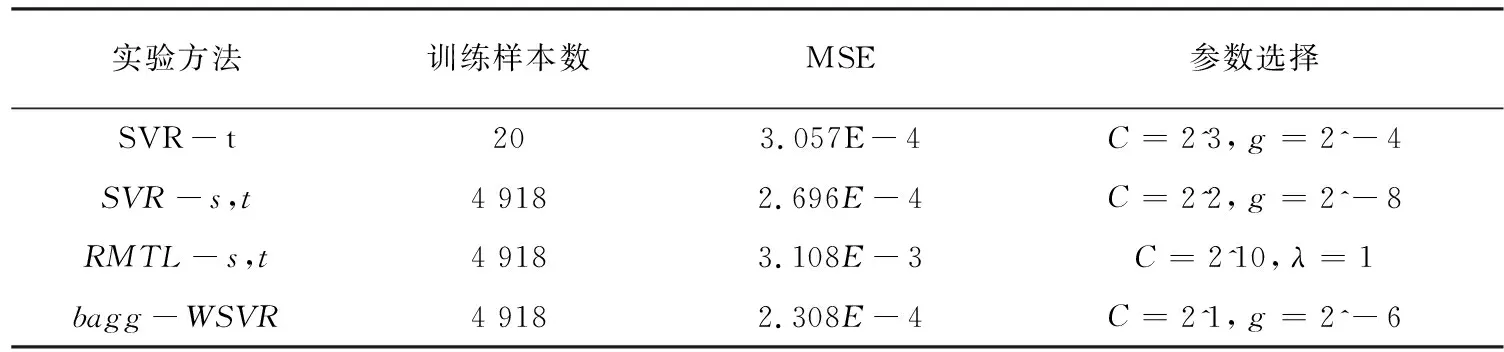
表2 wine数据集上各个模型的性能比较
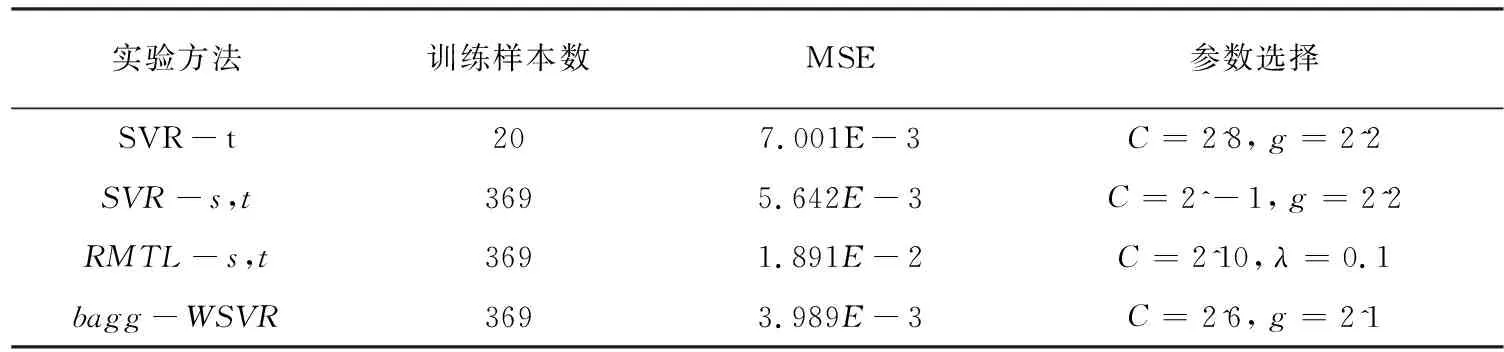
表3 student数据集上各个模型的性能比较
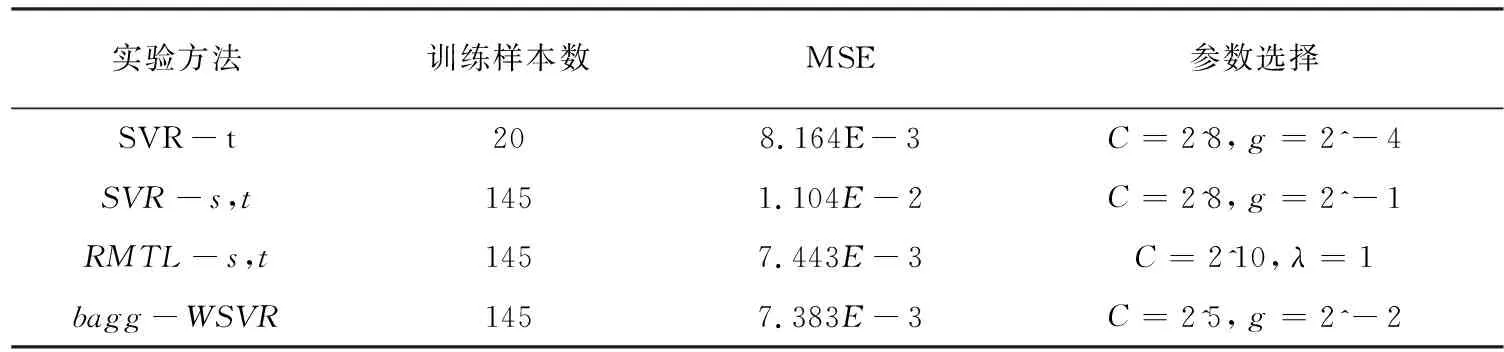
表5 粮食储藏数据集上各个模型的性能比较
由表2到表5可以看出:(1)当源域与目标域数据关联程度很大时,利用源域数据和目标域数据与标准ε-SVR算法建立的回归模型较只使用目标域数据和标准ε-SVR算法泛化性能好;当源域与目标域数据有关联,但是关联程度不太大时,利用源域数据和目标域数据与标准ε-SVR算法建立的回归模型较只使用目标域数据和标准ε-SVR算法泛化性能差,出现了“负迁移”现象。(2)改进的RMTL算法在小样本数据情况下的算法性能很不稳定,原因是目标域样本较少,导致标准ε-SVR算法建立的回归模型过拟合。(3)文中提出的算法在四个数据集上有着更好的泛化性能,因为文中算法根据源域中与目标域样本的相似程度,给相似样本赋予更大的权重数值;同时训练样本数目较大,防止生成模型过拟合现象产生,从而提高了泛化性能。
4 结束语
针对小样本数据情况下的回归系统建模问题,提出了一种小样本数据的迁移学习支持向量回归机建模方法。以加权ε支持向量回归机为Bagging算法的基学习器,使用与目标任务相关联的源域数据,通过自助采样生成多个子回归模型,采用简单平均法合成一个总回归模型。通过UCI数据集与现实数据集——玉米棒与花生粒储藏环节损失数据集的验证,结果表明该算法较标准ε-SVR算法与改进的RMTL算法在小数据样本上有更好的表现。但该算法也有一些不足之处:由于采用Bagging算法思想,有放回的抽样产生子数据集造成算法回归结果不稳定。下一阶段将改进子数据集产生的抽取方法,使源域中与目标域相似的样本更容易被选取,降低结果的不稳定性。

