计及电动汽车入网的冷热电微网系统优化配置研究

刘星月，唐 琳，雷 霖，廖先莉

(成都大学 电子信息与电气与工程学院，四川 成都 610106)

0 引 言

微网和冷热电联产(Combined cooling heating and power,CCHP)技术相结合，可提高能源利用灵活性和效率，冷热电微网系统是促进能源可持续利用和发展低碳经济的重要手段[1].

冷热电微网系统优化配置研究的重要意义之一，是为了减小机组配置成本和提高能源效率。文献[2]以多场景下微网系统年化总投资成本、维护成本与运行成本综合最低为目标，建立了多微网系统规划与运行相结合的双层多场景协同优化配置模型，验证了所提配置方法在经济性上的优越性.文献[3]利用蒙特卡洛法模拟风光负荷的不确定性，采用万有引力搜索算法得到风光储最优配置方案；此外，随着电动汽车(Electric vehicle，EV)的普及，对EV加以有序充电控制势在必行。文献[4]通过建立EV有序充电模型，考虑了主动配电网的多类管理手段，制定计及电动汽车和需求响应的配电网经济调度模型并验证了所提计及EV有序充电的经济调度模型的有效性.

目前的研究多见于优化电动汽车充电对电网调度的影响[5]，而涉及大规模EV充电对冷热电微网系统优化配置的影响较少.本研究通过构建EV 2种电价响应模式的有序充电模型，即移峰模式和削峰模式，来改善系统的负荷曲线，并建立了冷热电微网系统的结构及2种运行方式，构建了计及EV入网的冷热电微网系统优化配置模型，采用粒子群算法对模型进行计算，分析了系统运行方式、EV无序、有序充电模型对系统优化配置的影响.通过算例验证了本研究所建模型的有效性和正确性.

1 EV充电数学模型

归一化处理中国EV用户的调查统计数据，可将用户最后一次返程时刻t0近似为服从正态分布，EV日行驶里程S近似为服从对数正态分布[6].

1.1 无序充电

在此模式下，用户均在自己方便的时间充电，假设EV最后一次返程时间t0为入网充电时间ts，即

ts=t0

(1)

据日行程里程S可得需要充电的时长TC为,

TC=(SW)/(PCηEV)

(2)

式中，W为每千米耗电量，KWh/km;ηEV为EV的充电效率;PC为EV恒充电功率,/kW.

由ts、PC、TC可得第i辆EV各个充电时段的充电功率PEVi[t]，即，

(3)

采用蒙特卡洛模拟法分别模拟每辆EV每时段充电负荷，累计得到N-EVshuliang辆EV每时段充电负荷，

(4)

式中，PEV losd[t]为第t时刻的EV充电总功率，/kW；N-EVshuliang为入网EV的总数量.

1.2 有序充电

本研究所建立的有序充电模式是基于电价引导策略，假定k倍(参与有序充电调配率k,0≤k≤1)EV用户是理性的，将EV充电时刻延迟到电价低谷，以节省充电费用.则k倍EV用户选择充电时间ts为，

(5)

式中，tstart为低谷电价开始时刻，ΔT为低谷电价时段长，tend为低谷电价结束时间，rand(0,1)为0到1的随机数.

而1-k倍EV用户的ts仍满足式(1).根据各辆EV的ts、PC、TC可得单辆EV各个充电时段的充电功率，如式(3)，进而累计叠加得N-EVshuliang辆EV充电日负荷.

根据低谷电价时段(tstart,tend)的选择机制，可将有序充电模式分为移峰模式和削峰模式.

1.2.1 移峰模式

在移峰模式下，(tstart,tend)采用当地峰谷电价时段规定，即低谷时段(当日23：00～次日07：00).

1.2.2 削峰模式

在削峰模式下，(tstart,tend)的选择是以考虑了入网EV的系统总电负荷峰谷差最小为目标函数，采用粒子群算法寻优所得，寻优模型为，

(6)

式中，σload为考虑了EV削峰充电的系统总电负荷标准差，σload为(tstart,tend)的函数.其中低谷电价时长小于12 h.本研究采用粒子群算法对式(5)进行寻优.

2 系统能量流图及运行方式介绍

本研究的冷热电微网系统结构及能量流图如图1所示，虚线表示电能流，点虚线表示冷能流，实线表示热能流.PV表示光伏、PW表示风机、ES表示储能装置、GT表示燃气轮机、GRID表示电网提供电荷需求，GRID和ES可反向吸收多余电能，EV吸收系统的电能进行充电.GT发出电能的同时产生热能，一部分通过WHB余热锅炉向系统供热负荷需求，另一部分通过AR吸收式制冷机向系统提供冷负荷需求.GB表示燃气锅炉消耗天燃气产生的热能，一部分直接提供给系统的热负荷，另一部分通过AR向系统提供冷负荷，HS表示储热装置.

本定义系统的广义热负荷需求QH-M为，

QH-M=QH+QC/ηAR

(7)

式中，QH为热负荷需求；QC为冷负荷需求；ηAR为AR的工作效率.

据GT的工作形式及热电负荷满足的机制，可将系统的运行方式分为以热定电(Ordering power by heating,OPH)和以电定热(Ordering heating by power,OHP)方式.

2.1 OPH方式

系统的QH-M由GT提供，其中热负荷由GT通过WHB满足，冷负荷由GT通过AR满足，此时GB出力为0，GT、PV、PW同时产生的电能共同供给总电负荷，若有剩余由ES储能，若超过了ES的容量，向GRID售电获利；若产生的电能不够，由ES放电，若超过了ES的容量，由GRID补充.

2.2 OHP方式

系统总电负荷由GT、PV、PW、ES满足，GT同时产生的热能供给QH-M，若有剩余，由HS储存多余热能；如产生的热能不够，由GB补充，若超过了GB的容量，由HS补充.

3 优化配置模型

3.1 目标函数

本研究将机组折旧CDC、运行维护成本COM、污染气体处理成本CPO、外网交互成本CGRID统一折算为经济成本，作为目标函数.

minf=CDC+CPO+COM+CGRID

(8)

3.2 约束条件

1)系统电功率平衡

(9)

式中，Pj为机组所发功率，/kW；M为系统中机组的总数量；Pload为原始电负荷需求，/kW；PEVload为EV总充电负荷,/kW.

2)热功率平衡

QGT/ηWHB+QGB+QHS=QH-M

(10)

式中，QGT为GT提供的热功率，/kW；ηWHB为WHB的余热利用效率；QGB为GB提供的热功率,/kW；QHS为HS提供的热功率,/kW.

3)可控微源功率出力约束

(11)

式中下标min、max分别代表各机组最小最大出力.

4 仿真算例

选取成都市某居民小区为例进行研究，该小区的微网结构如图2所示，小区内目前有500辆EV，且小区内充电桩足够多，在EV有序充电模式下，假设k=0.8.该小区冷热电微网系统需要优化配置的机组容量包括PV、PW、GT、GB、AR、ES、HS，本研究仍采用粒子群算法求解上述构建的优化配置模型.

4.1 优化配置结果

为了分析EV充电模式及微网系统的运行方式对优化配置的影响，本研究设置了6种优化配置场景：场景1为OPH下EV采用无序充电模式，场景2为OPH下EV采用移峰充电模式，场景3为OPH下EV采用削峰充电模式，场景4为OHP下EV采用无序充电模式，场景5为OHP下EV采用移峰充电模式，场景6为OHP下EV采用削峰充电模式.求解以上6个场景下的优化配置结果如表1所示.其中机组配置容量单位为kW,配置成本单位为万元.

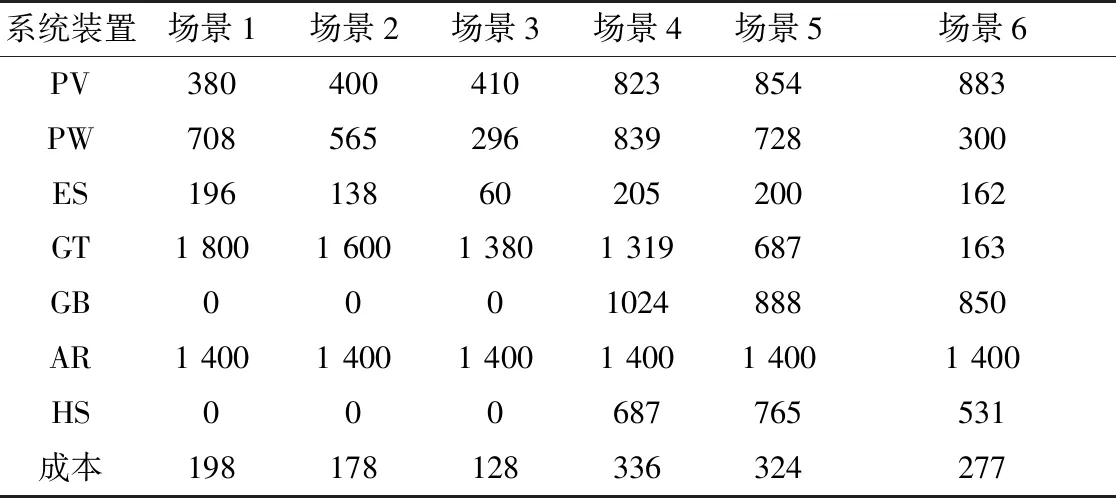
表1 优化配置结果

比较场景1、4时，场景2、5，场景3、6的结果，可知,当EV采用同一种充电模式时(无序、移峰、削峰)，OPH的运行方式在经济成本上优于OHP运行方式.

比较场景1、2、3，比较场景4、5、6，可知,当采用本研究设置的EV有序充电模式，可有效减小系统的机组配置成本，优化可控微源的容量，其中削峰模式的优化效果，优于移峰模式.

进一步研究3种充电方式对优化配置的影响，模拟案例中500辆EV分别采用无序、移峰、削峰(移峰和削峰模式下，k=0.8)3种充电模式时的EV充电日负荷，叠加在系统原始电负荷曲线上，得到3种充电模式下总负荷曲线.削峰模式下，根据图1的求解步骤可得最优低谷电价时段为02：30～10：15.

从图2可以看出，当EV采用无序充电模式时，其总负荷的峰谷差最大，其次为移峰模式，最小为削峰模式.结合表1可知，在无序充电模式下，夜晚的尖峰负荷最大，其PW配置容量最大，其次为移峰模式，最小为削峰模式.同理也可分析，无序充电模式下系统的峰谷差最大，为了迎合高峰时期的负荷需求，可控微源配置容量及配置成本最大，而移峰和削峰模式可改善系统负荷曲线，有效减少可控微源配置容量及配置成本，且削峰模式优于移峰模式.

4.2 EV有序充电模型有效性

为了验证本研究提出的电动汽车有序充电模型(移峰模式和削峰模式)的有效性，将本充电模型应用在文献[6]的算例系统中，并和文献[6]中3种EV充电模型(无序、正序、有序)做出对比假设此时系统中共有500辆电动汽车充电，具体如图3所示.

由图3可知，对比文献[6]的3种充电模式，本研究提出的移峰模式将充电负荷平移到了电价低谷时段(02:00～05：00)，有效地减小了传统负荷高峰(17：00-22：00)的用电压力，同时引起了新的一轮负荷高峰，而削峰模式可以弥补这个弱点，通过对低电价时段的寻优(所求最优时段05：00-13：00)，引导电动汽车用户将充电行为平滑过渡到最利于削峰填谷的时段，故其最利于平滑充电负荷.

进一步，当移峰和削峰充电模型与文献[6]所提3种充电模型应用在不同EV规模时，各种充电模式下系统总负荷的峰谷差率如表2所示.

表2 不同充电模式下总负荷峰谷差率

以上可知，当EV充电规模不同时，本研究提出的EV削峰充电模式在削峰填谷，平滑负荷方面，效果最优.

4.3 参与有序充电调控率及EV入网数目对优化配置成本的影响

进一步研究当 N-EVnumber和k变化时，对微网系统的优化配置的影响，如图4所示.

图4中x轴指k的变化值(0.2到1)，y轴(200到1 000)指N-EVnumber，z轴指配置成本(万元).当y值不变时，随着k的增加，配置成本减小，说明愿意参与有序充电调配的用户比例越大，对冷热电微网系统配置成本的优化越明显.而当x值不变时，优化配置成本随着y的增大而增大，因为随着EV数量的增加，系统的总电负荷需求增加，所需要的机组容量及成本都会增加，其增加的幅度随着EV的数量增加而减小，原因是EV用户中有一部分愿意参与削峰调配，故由于EV数量增加而导致的配置成本增加趋势得以减缓.

5 结 论

本研究建立了EV无序和有序充电的模型以及冷热电微网系统的结构，并设置了两种运行方式，最后建立了考虑EV入网的冷热电微网系统优化配置模型，采用粒子群算法进行求解，可知本研究所提有序充电模型可减小系统负荷峰谷差，因此可减少冷热电微网系统的配置成本，优化可控微源机组配置容量，其中削峰模式优于移峰模式。而在削峰模式下，EV用户参与有序充电意愿和EV入网数量也是影响系统优化配置的因素，在EV入网数量一定的前提下，用户参与意愿越强，对系统的配置成本优化效果越佳。本研究所建模型和结论可为结合了电动汽车和冷热电微网系统的研究提供参考。