基于架空轨道的全向移动机器人运动稳定性研究

徐 凯 林显新 易 丐 李国进

(1. 广西机电职业技术学院机械工程系，广西 南宁 530007；2. 广西大学电气工程学院，广西 南宁 530007)

随着机器人技术、互联网技术及人工智能技术的快速发展，出现了具有智能化运输系统的无人餐厅。当前的无人餐厅大多采用地面轮式服务机器人完成运输服务，其运动轨迹需要占用一部分就餐面积和过道面积，与用餐人员产生干涉，运动速度慢，场地利用率不高[1]。

试验拟构建空中轨道运输系统，采用麦克纳姆轮实现全向运动。机器人根据座位号将菜肴运送至指定位置，座位号定位采用程序轨迹控制，机器人在十字轨道内实现横向、纵向运动。采用STM32作为处理器，行走系统采用麦克纳姆轮在空中导轨内做横向、纵向运动，下部悬挂菜肴升降机构。机器人在做变向运动时受惯性力作用易失稳，通过建立数学模型，仿真研究其动态性能，优化参数配置，增强运动稳定性，为采用架空轨道移动的机器人构建空中物料搬运系统的稳定性提供参考。

1 系统数学模型的建立

在实现全向运动时，机身的稳定性是保障机器人能实现基本运动的要素之一。为了不影响就餐空间，机器人在架空导轨内运动，并在机器人重心正下方悬挂升降机构，实现上、下菜。影响机器人机身稳定性的因素有菜肴惯性力、轮子与导轨的摩擦力和转速，根据这3个干扰因素形成的非线性系统建立数学模型，并转化成线性系统模型分析该高阶系统。

1.1 建立系统数学模型

根据机器人控制的工作原理，忽略步进电机内部电磁机构的干扰，系统是由控制器、执行机构和干扰因素构成的简单的开环控制系统，其方框图如图1所示。

步进电机的工作原理：接收到控制器的脉冲，步进电机就转动一个角度。运用STM32F103FD单片机产生脉冲控制步进电机从而驱动4个ABAB麦克纳姆轮(见图2)，以控制4个轮子的转向来控制全向机器纵向移动。

图1 系统的数学模型

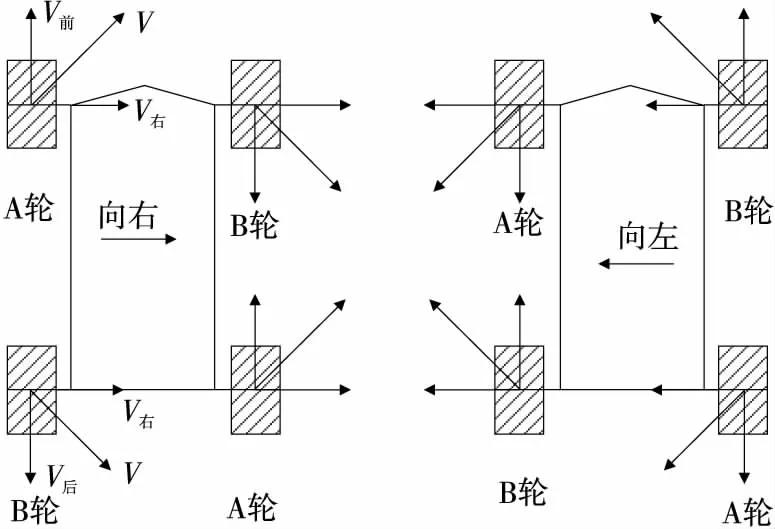
图2 驱动模式

由图2可知，两个A轮正转，两个B轮反转，实现机器人右移；两个A轮反转，两个B轮正转，实现机器人左移[2-3]。控制器发出的脉冲决定步进电机的运行状态，脉冲频率越大，步进电机速度越快，脉冲数量越多，电机旋转角度越大，脉冲发送速率直接决定电机转动速度。

而对于菜肴受惯性力作用导致机器人小车重心偏移的干扰，根据受力分析[4]，全向运动方式如图3所示。

1. 架空轨道 2. 麦克纳姆轮 3. 机器人机架 4. 步进电机5. 菜肴托盘 6. 挂绳

干扰因素则根据钟摆运动的牛顿方程描述：

m2a=fg+fd+fr，

(1)

式中：

fg——重心力，N；

fd——外强迫力，N；

fr——摩擦力，N；

m2——菜肴质量，kg；

a——菜肴的加速度，m/s2。

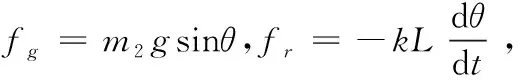
(2)

(3)

式中：

θ——惯性摆动角度，(°)；

k——摩擦因数；

L——挂绳长度，m。

1.2 构建系统方框图

控制器发出的脉冲频率决定步进电机的运行速度，控制器的传递函数为比例环节，Ka为环节的放大系数，即有G1(s)=Ka。若忽略步进电机内部线圈的电磁干扰，驱动机构中，麦克纳姆轮与地面之间的摩擦力f跟接触面粗糙程度和轮子接触面大小等有关，根据动力学方程，系统驱动机构的传递函数为：

(4)

式(4)为一个惯性环节与积分环节的合并。对菜肴进行牛顿方程受力分析时，考虑摆角不大的情况下有sinθ=θ，即有：

(5)

根据以上初步设计分析，确定系统传递函数方框图(其中系统的闭环回路指电机内部的位置环)见图4。

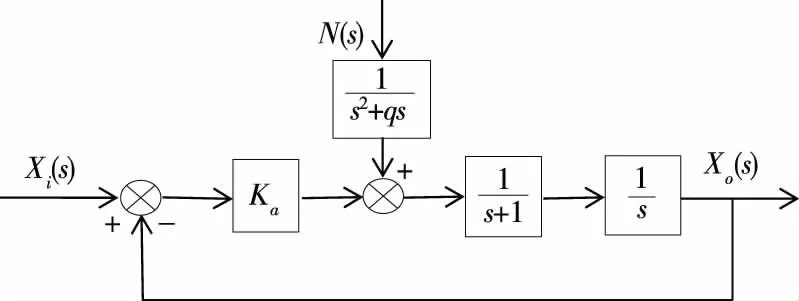
图4 系统传递函数方框图

2 分析系统的性能

系统性能的好坏直接影响到无人餐厅的运营，机器人振荡过大导致菜肴晃动，特别是汤品受影响最大，若系统稳定的调整时间过长会影响运输时间[5-7]。试验将分析影响系统性能的因素，保证其稳定性。

2.1 系统传递函数

当忽略干扰，即N(s)=0时，只考虑输入起作用的情况下：

(6)

当忽略输入，即Xi(s)=0时，只考虑干扰起作用的情况下：

(7)

2.2 系统性能分析

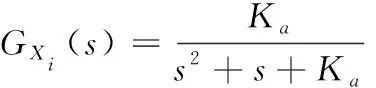
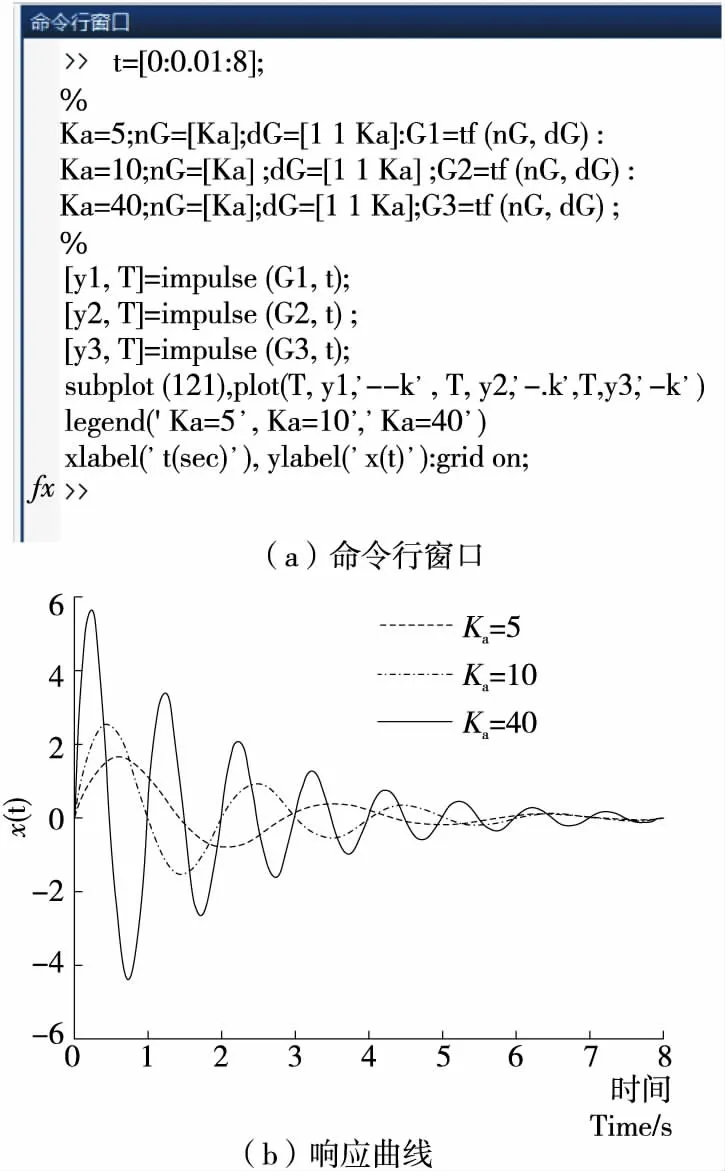
图5 系统无干扰的响应

由Matlab仿真曲线可知，系统经过多次振荡后趋于稳定，且Ka越大，振荡幅值越大，稳定调整时间越久。

由Matlab仿真结果可知，系统经幅振荡后趋于稳定，Ka越大，系统稳定调整时间越短，干扰影响越小。利用Matlab计算干扰和无干扰的阶跃响应时，Ka分别取5，10，40，分析系统的性能指标，如表1所示。

由表1可知， 无干扰响应时，最大超调量与调整时间随Ka的增大而增大；干扰响应时，最大超调量与调整时间随Ka的增大而减小，二者相互矛盾。最大超调量反映系统的相对稳定性，最大超调量越小，相对稳定性越好，而调整时间反应系统受冲击后恢复稳定的能力。因此，系统在有、无干扰情况下处在相对平衡时，存在中间值Ka，使系统保持在最优状态。

图6 系统有干扰的响应

3 分析增加反馈后系统的动态性能

由于步进电机的特性，该系统是开环控制系统，系统的输出端与输入端间不存在反馈，当因惯性扰动引起的被控制量偏离目标值后无修正能力[8-9]。开环控制系统具有结构简单、容易控制等优点，但由于没有反馈环节，系统的快速稳定性无法得到保证，而系统稳定性直接决定机器人的全向移动误差。因此，在程序控制中引入适当的速度反馈，降低系统最大超调量的同时缩短调整时间。

表1 不同Ka值下干扰和无干扰的瞬态性能指标

3.1 增加速度反馈控制

根据现场实际情况的需要，在初步系统设计(图4)基础上增加速度反馈控制，相当于步进电机内部位置反馈，如图7所示。

图7 系统速度反馈框图

编写驱动程序，在程序内部增加比较速度的反馈调节控制，即比较输出速度与给定速度，给定速度是由调试人员多次试验而得的一个最佳参考速度。再对该系统进行性能分析，当忽略干扰，即当N(s)=0、Ka=10时，只考虑输入起作用的情况下：

(8)

当忽略输入，即当Xi(s)=0，Ka=10时，只考虑干扰起作用的情况下：

(9)

3.2 分析校正后的系统性能

对系统进行稳定性分析，忽略干扰[N(s)=0]，单位脉冲输入作用下的响应曲线如图8所示。

加入反馈后的传递函数为一条相对平滑的曲线，没有振荡，即速度反馈系数Kc越大，系统性能越好。

通过速度反馈调节，改变反馈系数Kc，Kc越大对系统性能改善越明显。采用Matlab仿真无干扰和干扰的阶跃响应时，Kc分别取0.05，0.10，0.40，分析系统性能指标，如表2所示。

由表2可知，干扰和无干扰情况下，随着Kc的增大，调整时间逐渐减小，且超调量为零，由此可得出通过调整机器人运动速度可改善系统的稳定性能。

4 检验系统改善后的效果

调整4个麦克纳姆轮与地面同一水平，保证轮子与地面受力均匀[10-11]，现场调试全向移动机器人，为验证菜肴在运输过程中受冲击干扰影响最小时，获得机器人横向与斜向最佳运动速度，控制程序见图10。

图8 校正后系统无干扰的响应

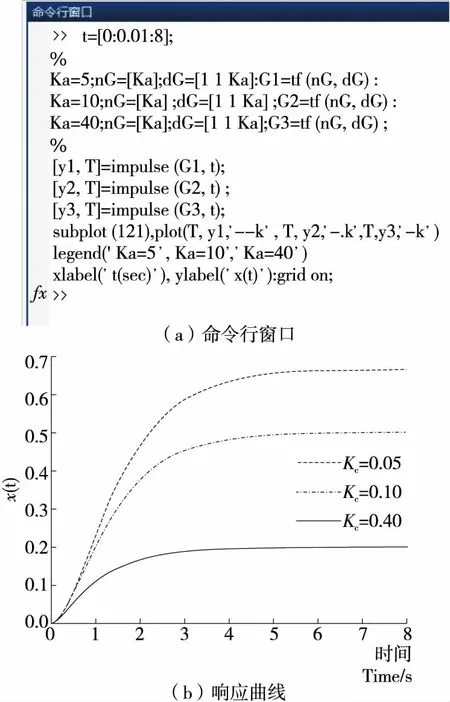
图9 校正后系统有干扰的响应

表2 不同Kc值下干扰和无干扰的瞬态性能指标

图10 程序调试

由图10可知，步进电机转速应<1 000 r/min，当转速为500 r/min时，步进电机扭矩下降得很厉害，因此控制程序中速度反馈对比的参考速度为100～200 r/min。由于步进电机运动速度与脉冲频率呈正比，通过编写驱动程序，设置定时器控制脉冲发送的频率，通过多次试验，最终确定当电机转度为135 r/min时，系统稳定调整时间最短，对系统稳定性影响最小。

5 结论

通过建立控制器、驱动机构和被执行对象的数学模型，分析被执行对象受惯性作用对系统性能的冲击干扰，提出采用控制程序中增加速度闭环反馈的方法进行修正。通过理论推导计算，根据Matlab仿真与现场调试，选择合适的反馈参数Ka和速度参数Kc，当步进电机转速为135 r/min时，系统调整时间最短，稳定性最好。结果表明，采用速度闭环控制方法能够达到预期效果。后续将从提高系统快速响应方面进行更深入探讨。