基于分数阶超混沌系统的无损彩色图像加密

◆王 勇 王 翔 王 瑛

（广东工业大学 广东 510006）

1 相关知识与创新

1.1 Qi 超混沌系统

针对传统Qi 混沌系统难以产生四翼，以及系统易被破解的不足，将传统的Qi 系统的非线性项改为更高次的三次项，通过实验结果证明生成的相空间更大，可以产生四翼超混沌吸引子，同时Lyapunov 指数具有两个正数，符合超混沌的特性，通过三次非线性的运算，可以有效地抵御选择明文攻击，将明文中每一个位置像素值之间的互相联系打破，使得明文图像像素值之间的影响扩散到了整个密文图像中，更加难以从密文中破解得到原图像。

传统Qi 混沌系统数学表达式为：

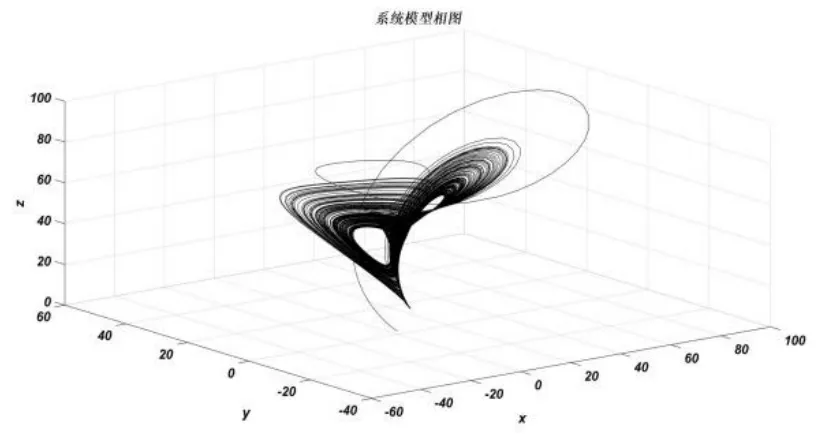
图1 Qi 混沌系统三维相图

由文献[3]知，当a=35，b=8/3，c=80，d=8 时，系统相图如图1 所示。

相比于传统的混沌系统，四翼超混沌系统具有更大相空间，可以提供更大的加密空间，本文在传统Qi 混沌系统上改进后的表达式为：

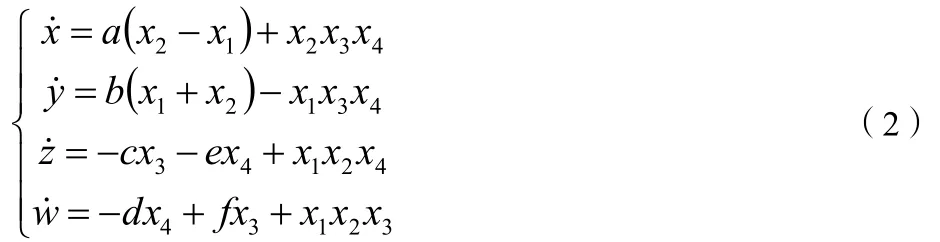
当参数a=50，b=10，c=13，d=5，f=30 时，系统的Lyapunov指数分别为：L1=3.82，L2=1.62，L3=-15.21，L4=-48.23，系统满足L1＞L2＞0 ＞L3＞L4，具有超混沌特征（见图2）。同时，该系统能够产生如图3 所示的一个真正的四翼混沌吸引子。

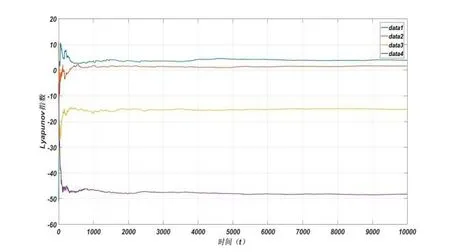
图2 超混沌系统随时间t 的Lyapunov 指数图

图3 四翼混沌吸引子

该系统的分数阶形式为：

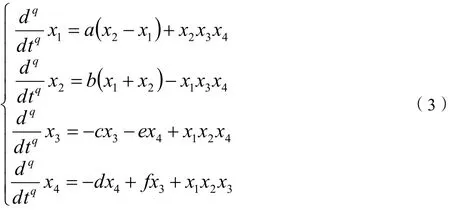
将系统（3）表示为矩阵形式，表述如下：

其中

1.2 二维离散小波变换

二维离散小波变换作为一种将信号进行分解和压缩的频域处理技术，因其具有多分辨率、局部时频、频率压缩的特性，使得其在图片编码、图像处理、图像压缩等领域得到广泛青睐。其核心工作原理是：首先对输入的信号源按行做小波分解，然后按列对获取到的中间数据再做小波分解。对输入的信号源一级离散小波变换后，信号源划分为四个子带：低频子带和高频子带如：对低频子带 LL1继续执行离散小波变换，可得到四个子带对低频子带连续执行n 次类似的操作，就可获得n 级变换的结果，将分解的子带进行IDWT 可以实现对图像的重构，得原始图像[4]。

离散小波变换含多类小波转换方法，包含Haar、Daubechies、Meyer 小波转换等。其中，本文采用的Haar 小波转换是最简单的一种转换，对图像不会造成信息损失，是一种无损的变换。

1.3 卷积神经网络

卷积神经网络（Convolutional Neural Network，CNN）作为一种前馈神经网络，其神经元可以响应部分覆盖范围内的周围单元，对于各类的图像处理有出色的表现。其主要的架构包括了卷积层（Convolutional Layer）和池化层（Pooling Layer）两部分。

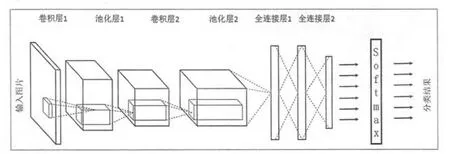
图4 卷积神经网络结构图

其中输入层是一个序列X=（x1,x2,x3...xn），输出层同样是一个序列Y=（y1,y2,y3...ym），各层之间的每一个连接上都有权值W=（w1,w2,w3...wn），本文中激励函数采用sigmoid 函数，其定义为：

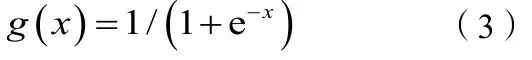
卷积神经网络的标准训练模式为：

式中，W0=W0，h＞0为学习步长，∇E（Wk）为E（Wk）在点Wk的梯度，本文根据生成的混沌序列的相关性，设计一个新的损失函数用来训练神经网络，由于当一组序列的相关性在0.2-0.4 之间的时候可以认定这段序列是弱相关的。新设计的损失函数：

式中，xYρ表示实际输出序列的相关性，Yρ表示期望输出序列的相关性，经过神经网络的训练使得到的混沌序列是弱相关的。

1.4 AES 加密算法

针对传统的AES 加密算法密钥和S 盒固定不变性的缺点，本文对传统AES 算法进行相应的改进，利用结合明文特性的混沌序列来设计出一个 1616× 的S 盒，并且通过随机置乱来产生密钥，首先对明文图像和目标密钥进行异或运算得到状态矩阵，然后进行2 轮循环加密。每一轮AES 算法分四步：

（1）字节代换：将状态矩阵里面的元素值映射成一个新字节，具体的映射规则是：每个元素字节的高4 位作为行坐标，低4 位作为列坐标，以此查询S 盒对应的值进行替换。

（2）行移位：对状态矩阵进行左循环移位操作。

（3）列混合：用一组固定矩阵与状态矩阵进行矩阵相乘，其中的矩阵乘法是定义在基于GF（2^8）的二元运算。

（4）轮密相加：将状态矩阵与目标密钥进行矩阵的逐位异或运算。

AES 加密过程如图5 所示：

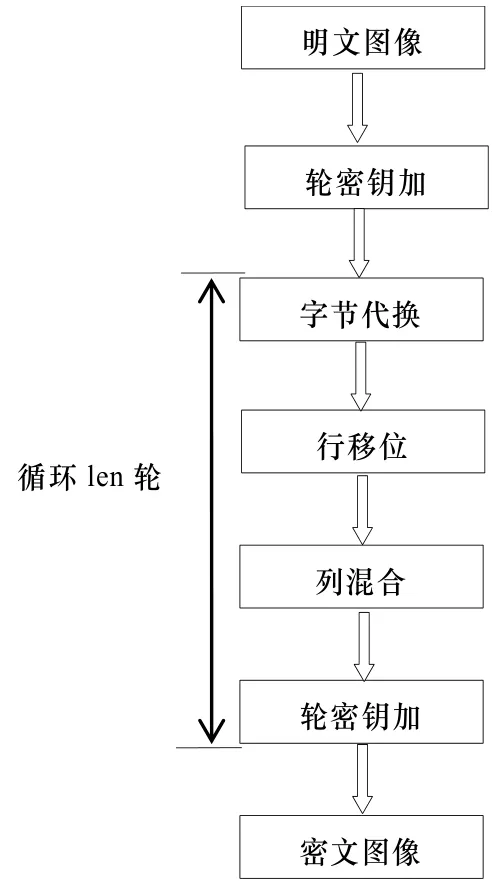
图5 AES 算法加密过程

1.4.1 明文相关参数

对于一个像素大小为NM× 的图像，设S是其像素值总和，avg 是其像素平均值，则t是与明文像素密切相关的控制参数，其中：

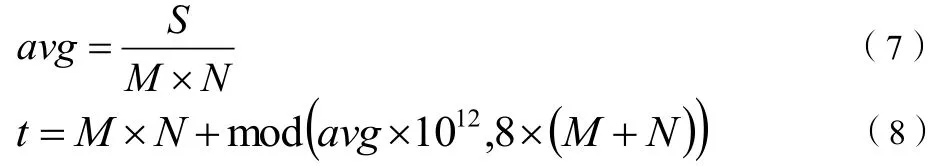
1.4.2 S 盒设计

为了去掉产生S 盒的序列出现重复的元素，同时保留其随机性，本文对S 盒进行如下改进：创建一个长度是256 的空数组Seq，循环读取结合明文特性的序列的数值同时插入对应索引值的Seq 中，若插入位置为空则插入，若所指位置已有元素，则一直查询数组的空位置然后插入，插入后将该位置的索引值，并得到一个全新的序列，然后将新的序列转换成16*16 的S 盒。

2 图像加密步骤

step1. 设彩色明文图像0I大小为NM× ，将彩色图像0I进行分离得到三个大小为NM× 的分量矩阵PR，PG，PB。

step2. 设超混沌系统的初始值x=1，y=1，z=1，w=1，循环次数为len=8 ×256×256，利用四阶龙格库塔公式对超混沌系统进行求解，得到一组新的数据{x，y，z，w}，将得到的数据{x，y，z，w}带入公式（9）求得变量r，当r=0 时，将{x，y，z，w}插入空序列D中；当r=1 时，将{x，y，z，w}插入空序列D中；当r=2 时，将{x，y，z，w}插入空序列D中；当r=3 时，将{x，y，z，w}插入空序列D中。如此循环len次，最后得到的序列 0D即为原始混沌序列。

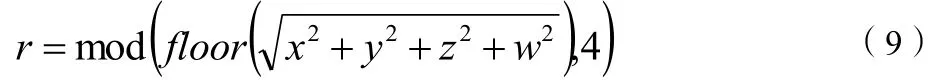
step3. 设定损失函数中的期望序列相关性ρY=0.3，权重均为随机初始化。将Step2 得到的原始混沌序列 0D作为输入，放到三层BP 神经网络中训练10000 轮后输出新的序列，训练后得到的新序列为 1D。

step4. 根据公式（8）分别计算明文图像分离的分量矩阵PR、目的是为了消除暂态效应带来的不良影响，然后选取256 位得到S 盒，用于分别给各基色图进行第一轮AES 加密，得到第一轮加

step5. 按照公式（10）对Step4 得到的密文图像1R，1G，1B进行二维离散小波变换，分别得到相应的四个小波子带。

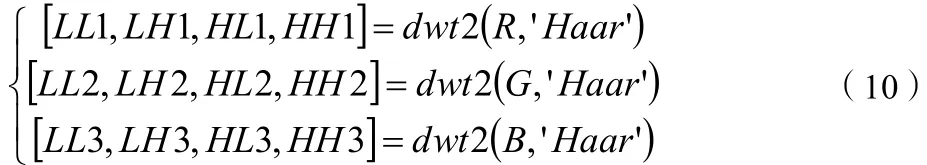
step6. 将Step4 得到的混沌序列rD，gD，bD根据公式（11）转化为（0，NM× ）的序列rT，gT，bT，公式如下：

step7. 将排序后的子带按照如式（12）所示进行逆变换重新转到空域，得到三个分量的密文图像，结合三个分量的密文图像得到最终的密文图像。

3 算法仿真与特性分析

3.1 算法仿真

本算法在Matlab2018a 环境下搭建并进行仿真实验，采用标准256× 256的Lena 彩色图像作为明文图像，超混沌系统初始值均设为1，加密后的图像如图6。

图6 图像加密和解密

3.2 算法统计特性分析

3.2.1 敏感性分析

评价一个加密算法效果的指标有很多，其中NPCR 和UACI是众多指标中尤为重要的两个，它们反映了一个加密算法对密钥产生改动后的敏感性，一个好的加密算法会对极小的密钥改动都极为敏感，它们分别的计算公式如下：

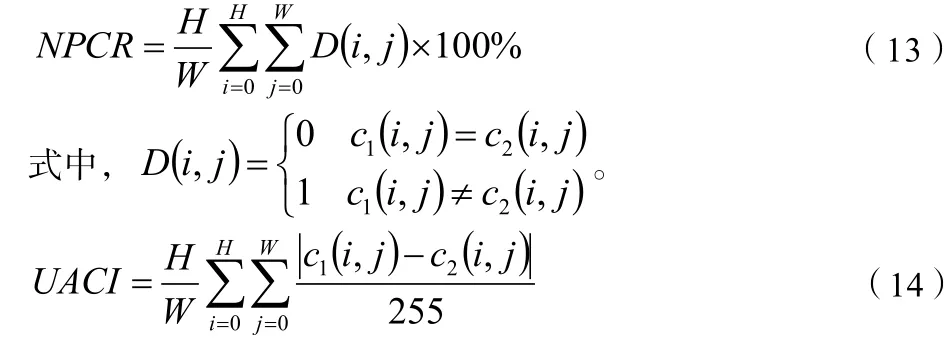
式中，c1、c2是加密过程中的密钥，NPCR 最佳100%，UACI最佳33.3%。

为了测试密钥的敏感性，本文选取其中的两个密钥进行测试，分别对两个密钥做轻微的改动，每次只改变一个密钥的值，第一次改变密钥Ur=0.25364156，观察最后的解密结果如图7a 所示；第二次改变密钥Ug=0.15263698，观察最后的解密结果如图7b 所示。通过图7 的显示表明本文提出的算法对密钥的敏感度较高，密钥的轻微改动就会使得解密后的结果仍然杂乱无章。同时，表1 列出了加密图像的NPCR和UACI 值，并和其他文献做了对比。

图7 密钥敏感性分析

表1 NPCR 和UACI 分析比较表

3.2.2 直方图分析

图像的直方图体现了图像像素的分布情况，有明显分布的直方图攻击者更加容易从像素的分布情况中获取信息，因此评价一个加密算法的好坏可以从图像的直方图分布情况来评定。图8 和图9 分别展示了明文图像和密文图像的分布直方图，可以看到明文图像分布上高低不一，具有明显的特征，而加密后的密文图像分布平均，更加难以找到密文图像的破解点。同时，从统计学角度分析，图像的方差可以证明直方图的均匀性的好坏，本文采用公式（15）的方法计算图像的方差，方差越低说明图像分布越均匀，分别计算图8 和图9 各个分量的方差，其结果见表2 所示。

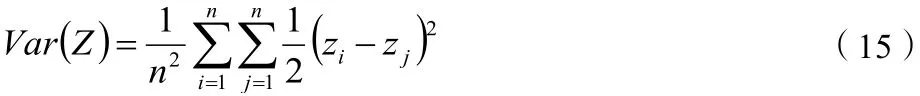
式中，iz和jz分别表示某两个像素点的出现次数，Z为各个色阶值在图像上出现次数的集合。

图8 明文像素直方图

图9 密文像素直方图

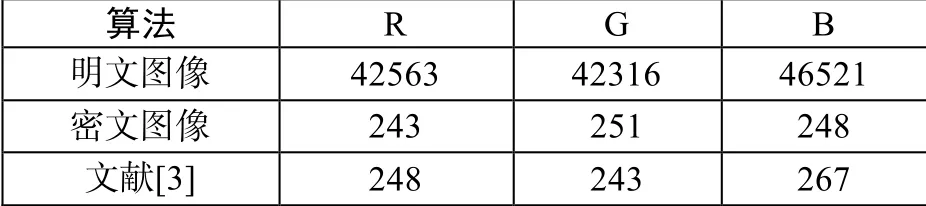
表2 明文和密文直方图方差比较表

3.2.3 相邻像素相关性分析

图像作为一种不同于文字的信息传输载体，每一个像素点与周边的像素点之间互相之间都存在强相关性，而且各个像素点之间也是相互依赖的，因此好的加密算法就要打破这种依赖性和强相关性。关于相关性系数的公式（16）—（19）如下：

式中，x，y 表示相邻两个像素的像素值，表示像素均值，D（x）表示方差，Cov（x,y）表示协方差，γxy表示相邻两个像素的相关系数。本文分别从不同的方向上选取5000 对相邻像素点绘制了如图10 和图11 所示的水平、垂直和对角方向上的相邻像素关系图。可以观察到，明文图像像素点明显分布上很密集，而密文图像分布更加随机，无规律可循。从表3 可知，明文图像相邻像素的相关性接近1。但是，密文图像的相关性明显降低，接近于0，证明算法打破了原有的相关性。同时，从表4 中，将本文的相关系数与文献[6，8]对比发现，本文的相关系数更低，因此具有更好的加密效果。

图11 密文相关性

表3 明文和密文像素相关性比较表

对角 0.9352 0.9384 0.9425 0.0028 0.0022 0.0019

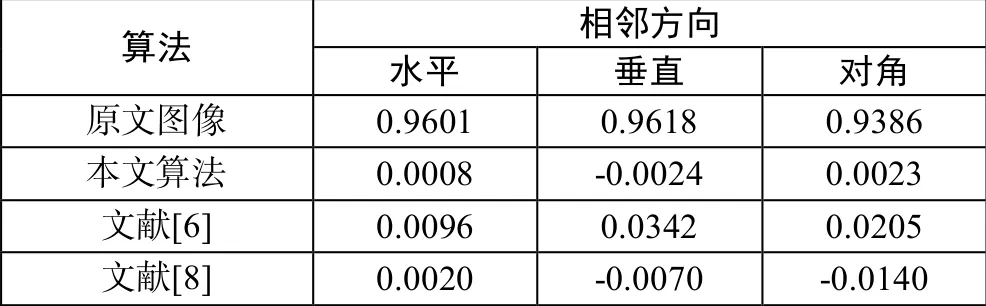
表4 不同算法像素相关性比较表

3.3 信息熵分析

信息熵作为判断信息量化度量的一个标准，主要用来描述信源的随机性，表示图像中像素值的分散状态，被越来越多的人用来评价图像信息量大小的一种标准。作为一种评价指标，信息熵的理想值是8，所以加密后的图像信息熵越接近于8，可以说明本算法的加密效果更好。信息熵的计算公式如下：

式中，xi表示像素值，表示像素xi出现的概率。

本文采用标准彩色Lena 图像分别对本文算法和文献[9-10]进行了测试，并在表5 中列出了分别测试后的结果。通过表5 可以发现本文的信息熵在加密后，相比于文献[9-10]更加接近于8。

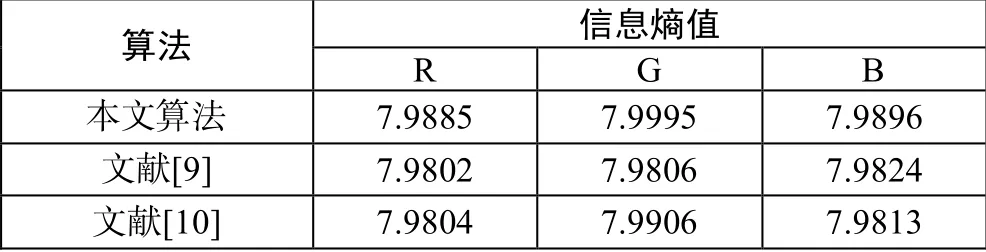
表5 不同算法信息熵比较表

4 结束语

本文针对传统Qi 混沌系统相空间小，易破解的不足，提出了一种改进的超混沌系统。同时结合BP 神经网络，设计适合本文算法的损失函数对经过超混沌系统得到的混沌序列进行二次置乱，利用基于此得到的混沌序列结合重新设计S 盒的AES 加密算法对明文图像进行第一轮加密。同时针对当前密文图像无法压缩问题，结合二维离散小波变换将图像进行第二轮频域加密得到密文图像。通过特性分析表明，本文的加密算法在新型混沌系统上产生了更大的相空间，并且最终生成的密文图像比同类算法相关性低接近10 倍，可以有效地抵挡当前难以解决的选择明文攻击方式。在此基础上，针对未来随着硬件的不断发展，破解手段更加多元化的情况，将继续研究更多的针对更多元攻击的加密算法。