交互作用多模型集成航迹分裂目标跟踪方法*
桑 航,周云锋,周共健
(1.哈尔滨工业大学电子与信息工程学院,黑龙江 哈尔滨 150001; 2.对海监测与信息处理工业和信息化部重点实验室,黑龙江 哈尔滨 150001; 3.中国电子科技集团公司第二十九研究所,四川 成都 610036)
多目标跟踪是一种处理观测数据的过程,它通过处理雷达、声呐等传感器传回的数据来发现目标,并估计目标的运动状态。近年来,目标跟踪在民用领域中得到了广泛的应用和飞速的发展,跟踪算法也与我们的日常生活紧密联系。例如,现在人们日常出行的GPS导航就用到了目标跟踪,基于GPS导航系统中的目标跟踪算法,我们才能享受到GPS导航系统带来的便利。此外,目标跟踪技术在空域监视、视频监控、气象监控、细胞生物学中有着广泛的应用。
在目标跟踪算法的实际应用场景中,通常充满了电磁杂波,这些杂波会影响到跟踪的精度。在杂波密度较高时,目标跟踪的发现概率会大大降低,同时也会出现虚假航迹,造成跟踪失败的结果。杂波环境下如何提高目标跟踪概率,同时抑制虚假航迹率是目标跟踪领域永恒的主题。
在多目标跟踪问题中,当目标间距离较近时,将无法判定观测来自哪个目标。我们可以利用数据关联方法将接收到的多个观测分配给多个目标。数据关联以概率的形式计算观测的来源,它假设观测来源的可能性,并计算每个假设的概率。数据关联是密集杂波背景下多目标跟踪的核心,目前使用较多的是贝叶斯类数据互联算法。
在之前的研究工作中,已经实现了概率数据关联算法,并利用交互作用多模型对机动目标进行跟踪。交互式多模型-集成概率数据关联(IMM-IPDA)是IPDA算法的机动目标拓展,由Mušicki和Suvorova于2008年提出[1]。对于多目标情形下的目标跟踪,多数方法容易受观测-航迹联合分配组合爆炸问题的严重影响。Mušicki和La Scala在2008年提出了线性多目标跟踪方法以解决这类问题。线性多目标(LM)跟踪方法是一个将单目标跟踪转移到多目标跟踪中的过程[2],其运算量与目标及观测数量呈线性关系。
本研究提出的集成航迹分裂目标跟踪方法对集成概率数据关联算法进行航迹分量的拓展。采用交互作用多模型(IMM)对机动目标进行跟踪,利用线性多目标方法(LM)对多个目标进行跟踪。
本研究的目的是提升多目标跟踪算法在高杂波密度、低发现概率环境下的性能,尽可能减少航迹分量的拓展带来的计算量增大的影响,并对具体的问题设计了仿真实验,其结果证明了该算法是有效可行的,相比原来的概率数据互联算法在性能上有较大提高。
1 单目标跟踪
传感器给出的观测(距离、角度、多普勒速度)是非线性的,因此本文使用量测转换卡尔曼滤波器处理观测数据[3]。
1.1 系统模型
首先是系统的状态方程。

X(k+1)=F(k)X(k)+V(k)
(1)
其中F(k)为系统的转移矩阵。V(k)为零均值、白色高斯过程噪声序列,协方差为Qk。
然后是系统的观测方程。
Z(k)=hk(Xk)+Wk
(2)
hk(Xk)可表示为

(3)

1.2 量测转换卡尔曼滤波器(CMKF)
1.2.1 量测转换
在本研究中,观测量是以距离和方位的形式给出的,为极坐标情形下的量测值。目标的状态向量是以笛卡尔坐标系为基准的,因此量测与目标的状态向量之间有着很强的非线性。为了便于计算,在进行滤波之前,首先应把极坐标下的量测转换到笛卡尔坐标系下。同时,也要对转换后量测值的协方差矩阵进行估计。文献[4]详细给出了将极坐标系下的量测转换到笛卡尔坐标系下的过程。
1.2.2 卡尔曼滤波
卡尔曼滤波用来计算感兴趣目标的后验概率密度,在本研究中用来计算航迹状态的后验概率密度,同时计算航迹状态的观测似然函数。卡尔曼滤波估计主要分为三个部分:卡尔曼滤波预测、目标观测预测、卡尔曼滤波估计[5-6]。
卡尔曼滤波已经是非常成熟的估计方法,本文就不再进行赘述了。
1.3 交互作用多模型(IMM)
在实际的目标跟踪应用场景中,目标的运动特性将随着时间不断变化,这类目标被称为机动目标。最典型的例子是战斗机。战斗机常常会做出加速、减速、急转弯等动作,此时若采用单一的模型对其进行跟踪,则很容易丢失目标。本研究基于交互作用多模型算法[1],对集成航迹分裂目标跟踪方法进行具体的实现。
IMM需要考虑d2个模型的状态,其中d为模型的个数[1]。每一个模型对应一个状态方程
xk=Frk·xk-1+vrk
(4)
其中,vrk~N(vrk;0,Qrk),rk为模型的编号,rk∈{1,2,…,d}。IMM是包含了d个模型的目标跟踪方法。
IMM是一个递推的过程,在上一时刻输入目标各模型的后验均值和协方差以及模型概率。对于本研究来说,输入为目标各航迹分量的后验均值和协方差以及模型概率。经IMM预测过后,得到航迹分量各模型的预测均值、预测协方差和模型预测概率,在滤波阶段再对它们进行更新。
1.4 IMM-ITS航迹初始化与航迹管理
ITS的算法是一个递推的过程,但是在航迹起始的时候是无法递推的,需要对航迹状态进行初始化。除了一些人为的设定,航迹初始化大多数情况下依赖于观测值。航迹初始化仍然比较缺少准确的理论,本研究只对其进行简单的探讨。如果航迹初始化的方法选择不好,则可能引起一系列跟踪上的困难,要么产生过多的虚假航迹,要么一些真实航迹没有被及时地初始化。这两种情况应尽量避免。
1.4.1 两点初始化
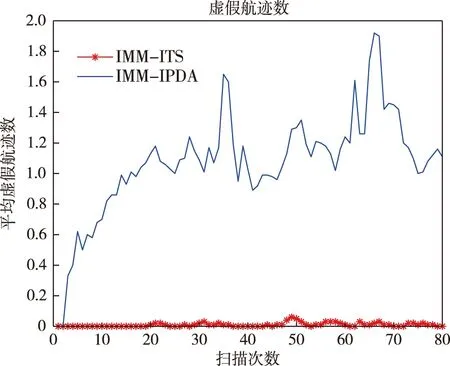
本研究采用两点差分法[10]来进行航迹的初始化。这个处理过程对k-1时刻的所有观测重复执行,设k-1时刻观测为Yk-1(j)。在下一个扫描时刻k,以Yk-1(j)为中心建立波门,两次观测的时间间隔为ΔT。这里采用速度波门,即利用当前时刻量测Yk(i)与中心量测Yk-1(j)计算出速度v,若满足v 新航迹是被观测Yk-1(j)和每个被选定的观测i=1,…,mk初始化的。新航迹的后验航迹状态估计在给定Yk-1(j)和Yk(i)后是一个高斯概率密度函数,均值为 (5) 协方差为 (6) 空观测也将对应一个航迹分量,其均值为 (7) 协方差为 (8) 其中In为n阶单位阵,这里是用每一个量测来初始化一个航迹分量的。每个航迹分量所对应的所有目标模型σ均用同一个状态估计概率密度函数来进行初始化。假设模型的个数为M,则每个目标模型的初始相对概率为1/M。 由于k-1时刻没有关于目标速率的先验知识,因此k时刻的先验概率密度函数由均匀分布来描述 Pk(i)=1/Vk (9) 其中Vk为波门大小。 除了对目标状态进行估计,IMM-ITS的航迹状态还应对目标各模型的相对概率进行初始化。 此外,目标存在的概率有一固定的初始值,然后根据马尔科夫链进行演化。 1.4.2 航迹管理 航迹的维持与管理是目标跟踪中非常重要的部分。它主要包含两个部分,一是真实航迹的确认,二是虚假航迹的剔除,这两项工作主要通过航迹质量来进行判定。 航迹状态的具体演化过程如图1所示。航迹的状态主要分为三类:暂时航迹、确认航迹和终止航迹。 图1 航迹状态演化过程 每条航迹在起始的时候都是暂时航迹,随着航迹状态的更新,航迹质量(目标存在概率)将产生变化。当目标存在概率超过预先设定的航迹起始门限值τc,则航迹变为确认航迹,并保持这一状态直到航迹变为确认航迹。当目标存在概率低于预先设定的航迹终结门限值τt,则航迹变为终止航迹,航迹将不被更新。 ITS更新时一个递推更新,在k时刻,输入为传感器产生的观测集Yk,目标存在性概率p(χk-1|Yk-1)每个航迹分量ck-1的相对概率p(ck-1),各分量每个模型对应的均值xk-1|k-1(ck-1,σ)与协方差Pk-1|k-1(ck-1,σ)。 1.5.1 航迹质量预测 航迹质量即目标的存在性概率。本研究采用文献[7]给出的马尔科夫链一模型。马尔科夫链一目标存在性模型定义两个互斥完备事件,记为随机变量Ek。 χk:Ek=1目标存在的事件; 目标存在性概率的演化遵循马尔科夫链演化公式 (10) 式中,γ为目标存在性的转移概率矩阵 γij=p(Ek=2-j|Ek-1=2-i) (11) 其中 i,j∈{1,2} (12) 且有 γ11+γ12=γ21+γ22=1 (13) 1.5.2 航迹概率密度预测 本研究利用卡尔曼滤波对航迹的状态进行估计。航迹概率密度函数预测可以转化为航迹的预测均值xk|k-1(ck-1,σ)和预测协方差Pk|k-1(ck-1,σ)。这里的预测分别对各个航迹分量进行,而不是对各个航迹进行,这样在更新的时候更能充分地利用到航迹分量。这也是ITS与IPDA的一大不同点。 预测利用目标运动模型来进行 (14) (15) 其中,F为目标运动的状态转移矩阵,Q为状态噪声的协方差矩阵。 1.5.3 观测似然函数 ITS分别对每一航迹分量进行估计状态预测,而观测选择就依托于得到的航迹预测状态。对于ITS,观测选择应对每一航迹分量的每一对应模型进行,再将所有被选中的观测组成一个合集,这一合集即为预选观测集。若观测y满足 (16) 其中g为波门大小的平方,则该观测被选中。 1.5.4 杂波密度估计 空间稀疏性估计方法对每个观测进行杂波密度估计,与航迹无关。它并不是直接估计杂波观测密度,而是估计杂波观测密度的倒数[8]。杂波观测稀疏性定义为杂波密度的倒数。 在观测y处的n阶空间杂波稀疏性γ(y)的估计步骤如下 1) 寻找观测y与其他量测之间的第n小的距离; 2) 计算 γ(y)=V(r(n)(y))/n (17) 这里V(r)是半径为r的超球体的体积。假设观测空间维数是,伽马函数表示为Γ(),则 V(r)=Cr (18) (19) 1.5.5 暂时航迹分量的建立 (20) (21) (22) 1.5.6 暂时航迹分量的建立 1.5.7 跟踪估计输出 目标状态的后验概率密度为高斯和的形式[9],均值和方差如下 (23) 在高杂波密度的情况下,如果采用联合集成分裂(JITS)方法进行目标跟踪,其复杂度将呈爆炸式增长,在实际应用中实现起来非常困难。本研究采用一种次优的多目标跟踪算法框架——线性多目标跟踪(Linear Multi-target)[2,8]。线性多目标跟踪方法将单目标跟踪转移到多目标跟踪中,其运算量与目标数和量测数呈线性关系。在极大地降低跟踪所需的计算量的同时,其性能还能与最优多目标算法的跟踪性能相差不大。 在线性多目标跟踪方法中,每条航迹对应的预选观测集中的观测有三种情况: 1) 被该航迹所跟踪目标的观测量; 2) 杂波观测; 3) 被其他航迹所跟踪目标的观测量。 线性多目标跟踪方法的核心思想是将来自其他航迹所跟踪目标的观测也看作一种杂波,将这种杂波加入到原先的杂波密度的计算当中,得到新的修正后的杂波密度。利用这一修正的杂波密度可以利用单目标跟踪方法来进行多目标跟踪。 线性多目标方法的具体实现在文献[2]中已经进行了详细介绍,本文不再赘述。 总体来说,将LM与单目标跟踪方法ITS结合得到IMM-LMITS主要分为两步: 1) 计算预选观测关于各航迹的先验概率Pτ(i)。若观测i未被航迹τ选中,Pτ(i)为零; 2) 进行数据关联的时候,用调制的杂波观测密度Ωτ(i)替换原来的杂波观测密度ρk(i)。 利用IMM-ITS和IMM-IPDA对单目标情形下的目标跟踪进行仿真实验,观察仿真结果。 3.1.1 运动模型 通过Matlab对IMM-ITS进行仿真实验分析。假设有一个目标在监视区域内运动,其运动模型有四个,分别是匀速直线(CV)、匀加速直线(CA)、匀速左转弯(CT)和匀速右转弯(CT)。 (24) (25) (26) 其中,Ωk为目标的转弯角速度,在本仿真中,Ωk分别取π/9 rad/s和-π/9 rad/s。 3.1.2 仿真环境 一个目标在[1 000,2 000]m×[400,900]m范围内作运动,其初始状态为: x1=[1 900 m,-18 m/s,690 m,0 m/s]T 运动分为8个阶段,每个阶段10 s: 1) 两目标均做匀速直线运动; 2) 目标做指数加速运动,每个方向上的加速度为a=v0αexp(αt),α=0.05 s-1; 3) 目标做指数减速运动,每个方向上的加速度为a=v0αexp(αt),α=-0.05 s-1; 4) 目标做匀速转弯运动,角速度为-π/9 rad/s; 5) 目标做指数加速运动,α=0.05 s-1; 6) 目标做指数减速运动,α=-0.05 s-1; 7) 目标做匀速转弯运动,角速度为π/9 rad/s; 8) 两目标均做匀速直线运动。 在[1 800,2 050]m×[550,750]m和[1 200,1 450]m×[700,900]m区域内还存在着较密集的杂波,以模拟更加真实的环境。 该仿真实验的各项参数如下: 在大部分区域,杂波密度为2e-5m-2,在密集杂波区域,杂波密度为10e-5m-2。检测概率PD为0.9,波门概率PG为0.99,雷达的观测噪声的距离标准差为1 m,角度标准差为0.001 rad,扫描次数为80次,扫描间隔为1 s。目标的最大速度为50 m/s,最大加速度为3.5 m/s2,最大角速度为π/5 rad/s。航迹的初始存在概率为0.05,航迹的确认门限为0.95,航迹的终结门限为0.3,航迹分量的终结门限为0.2,航迹分量的子树裁剪深度为3,航迹分量的终结门限为0.2。实验的蒙特卡洛仿真次数为100。 模型的转移概率矩阵为 (27) 3.1.3 仿真结果 图2分别展示了IMM-ITS和IMM-IPDA对目标的跟踪结果。可以看出两者均较准确地成功对目标进行了跟踪。但是IMM-IPDA存在着很多虚假航迹。 图2 IMM-ITS与IMM-IPDA的目标跟踪结果对比 图3所示为IMM-ITS和IMM-IPDA目标跟踪的真实航迹率。可以看出两者均很快就确认了真实航迹的存在。但是在后续对真实航迹维持中ITS的性能要远远优于IMM-IPDA。 图3 IMM-ITS与IMM-IPDA的真实航迹数对比 图4为IMM-ITS和IMM-IPDA目标跟踪的虚假航迹数。可以看出IMM-ITS的虚假航迹一直维持在一个很低的水准,而IMM-IPDA大多时候的平均虚假航迹超过了1。 图4 IMM-ITS与IMM-IPDA虚假航迹数对比 3.2.1 仿真环境 两个目标在[1 000,2 000]m×[400,900]m范围内作运动,其初始状态为: x1=[1 900 m,-18 m/s,690 m,0 m/s]T x2=[1 900 m,-17 m/s,650 m,2 m/s]T 运动分为八个阶段,每个阶段10 s: 1) 两目标均做匀速直线运动; 2) 两目标均做指数加速运动,每个方向的加速度为a=v0αexp(αt)。对于第一个目标,α=0.05 s-1;对于第二个目标,α=0.04 s-1。 3) 两目标均做指数减速运动,每个方向的加速度为a=v0αexp(αt)。对于第一个目标,α=-0.05 s-1;对于第二个目标,α=-0.04 s-1。 4) 两目标均做匀速转弯运动。角速度均为-π/9 rad/s。 5) 两目标均做指数加速运动,对于第一个目标,α=0.05 s-1;对于第二个目标,α=0.04 s-1。 6) 两目标均做指数减速运动,对于第一个目标,α=-0.05 s-1;对于第二个目标,α=-0.04 s-1。 7) 两目标均做匀速转弯运动。角速度均为π/9 rad/s。 8) 两目标均做匀速直线运动。 在[1 800,2 050]m×[550,750]m和[1200,1450]m×[700,900]m区域内还存在着较密集的杂波,以模拟更加真实的环境。 该仿真实验的其他参数与单目标情形相同。 3.2.2 仿真结果 图5为IMM-LMITS与IMM-JIPDA多目标跟踪的结果比较。可以看出两种跟踪方法对两个目标的跟踪效果较好,没有出现航迹的混合等问题。但是,IMM-JIPDA依然存在虚假航迹过多的问题。 图5 IMM-LMITS与IMM-JIPDA的目标跟踪结果对比 图6为IMM-LMITS与IMM-JIPDA对多目标进行跟踪的真实航迹率的比较。可以看出对多目标进行跟踪时,两者均很快确定了真实航迹,但是IMM-LMITS维持航迹的性能要远优于IMM-JIPDA。 图6 IMM-LMITS与IMM-JIPDA的真实航迹率对比 图7为IMM-LMITS与IMM-JIPDA的虚假航迹率对比。从图中可以看出,IMM-LMITS虚假航仍然维持在一个很低的水准,而IMM-JIPDA的虚假航迹率要高不少。 图7 IMM-LMITS与IMM-JIPDA虚假航迹数对比 在高杂波密度、低检测概率的环境中,如何在维持真实航迹的情况下仍旧将虚假航迹控制在一个较低的水平是一个非常重要的课题。在实际的应用中,目标跟踪还面临着目标机动频繁、剧烈的挑战。本文对IPDA算法进行航迹分量上的拓展,对ITS算法进行深入研究,并结合交互作用多模型实现了对机动目标的跟踪,进行了Matlab仿真。 对机动多目标的跟踪是在实际应用中最常遇到的问题,也是对目标跟踪方法性能的一大考验。IMM-LMITS在目标高机动、高杂波密度、较低检测概率的情形下表现良好,维持航迹、剔除虚假航迹方面的性能远远优于IMM-JIPDA。但是,该方法对于由转弯模型转变到加速模型的跟踪性能提升并不明显,仍需改进。



1.5 IMM-ITS航迹更新过程

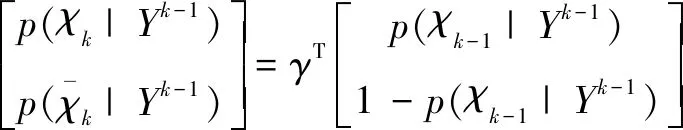

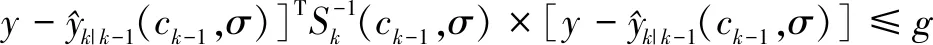








2 多目标跟踪
2.1 线性多目标跟踪
2.2 IMM-LMITS航迹更新过程
3 仿真分析
3.1 单目标仿真





3.2 多目标仿真



4 结束语

