适合于大气激光通信的双空间调制

王惠琴，杨顺信，李亚婷，武 鑫

(兰州理工大学 计算机与通信学院，甘肃 兰州 730050)

1 引 言

大气激光通信由于其保密性好、性价比高等特点，成为一种新型宽带接入技术。随着数据传输业务量的急剧增加，人们对大气激光通信系统的容量和传输速率提出了更高的要求，同时，大气湍流的存在会严重影响激光通信系统的有效性和可靠性[1]。因此，对大容量、高速率的大气激光通信系统提出了更为迫切的需求。

面对大气激光通信中存在的问题，目前主要的解决措施有轨道角动量[2]、成像通信[3]、光多输入多输出(Optical Multiple Input Multiple Output，OMIMO)[1]和光空间调制(Optical Spatial Modulation，OSM)[4]等。轨道角动量可大大提高通信系统的信道容量，但量子偏振涨落等现象会严重影响通信系统的性能。同时，由于其理论和模型还不完善，使其应用受到了一定限制。成像通信虽能获得较高的复用增益，但对位置信息较为敏感，而且无法满足移动性和无缝覆盖的需求。OMIMO技术可以在不增加频谱资源和发射功率的情况下，成倍提高现有系统的信道容量，但信道间干扰和多个激光器同步等问题导致其推广应用受到限制。与上述几种方法相比，OSM不仅采用传统数字调制星座(即数字域)传递信息，而且通过激光器索引号(即空间域)额外携带信息。因此，激光器不仅是形成无线链路的媒介，而且承载着信息比特本身。

早期的OSM起源于室内可见光通信[5]。与开关键控(On-Off Keying，OOK)和脉冲位置调制(Pulse Position Modulation，PPM)相比，OSM的提出将频谱效率分别提高了2倍和4倍[6]。与脉冲幅度调制(Pulse Amplitude Modulation，PAM)相比，二者具有相同的频谱效率，但OSM能提供更高的能量效率。学者们围绕如何设计高效的OSM方案展开了广泛的研究[7-14]。文献[7-10]分别采用PAM和PPM调制构建了不同的OSM方案。其中，文献[7-8]采用PAM调制提出了不同的OSM，实现了频谱效率的提高，但却带来了能量损失。文献[9-10]利用PPM调制构建了OSM方案，获得了较高的能量效率和较好的误码性能，但其频谱效率较低。随后，研究人员围绕室外大气激光通信中的OSM展开了研究[11-12]。其中，文献[11]将OSM和脉冲位置幅度调制(Pulse Position Amplitude Modulation，PPAM)相结合，构建了一种适合于大气激光通信的空间调制方案，实现了频谱效率和能量效率间的折中。文献[12]分析了几何扩散对OSM系统性能的影响，并推导了OSM在Gamma-Gamma信道中的误码率。

但在上述研究中[5-12]，每次传输仅激活一个激光器，虽然这有效地消除了信道间干扰和发送激光器同步的问题，但这要求激光器数必须为2的整数次幂，从而大大限制了空间资源的利用率。文献[13]采用PAM调制，通过同时激活少量的激光器构建了一种室内的光广义空间调制(Optical Generalized Spatial Modulation，OGSM)。该方案不仅解决了激光器数必须为2的整数次幂的不足，而且大大提高了系统的频谱效率和传输速率。文献[14]利用PPM调制构建了一种OGSM方案，有效地增加了系统的能量效率。上述两种OGSM在频谱效率和传输速率上虽然有很大的提升，但其误码性能还不够理想，并且相关研究仅分析了它们在室内可见光通信中的性能。鉴于此，本文通过同时激活两个激光器分别发送PPM和PAM调制符号，提出一种适合于大气激光通信的双空间调制(Double Spatial Modulation，DSM)方案，该方案有效提高了误码性能，有望进一步提高大气激光通信的传输速率。

2 DSM系统模型

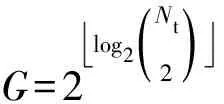
G=2log2Nt2()

·

表示向下取整运算。

log2Nt2()

m=log2Nt2()+log2M+log2L。

图1中，假设每次传输的信息比特为b，它经串并转换后分为b1，b2和b3三部分。其中，b1被映射为系统中激活激光器序号的组合(l1，l2)，其长度为比特。b2被映射为传统M-PPM调制星座图中的某个调制符号，其长度为log2M比特。b3被映射为传统L-PAM调制星座图中的某个调制符号，其长度为log2L比特。因此，DSM系统每次传输的比特数为当Nt=4，M=4，L=2时，每次可传输5比特的信息。假设传输的二进制信息比特为b=[1 0 0 1 1]，经双空间调制后，b1=[1 0]被映射为激活激光器序号组合(1，4)，b2=[0 1]被映射为传统4-PPM调制的调制符号，b3=[1]被映射为传统2-PAM调制的调制符号。

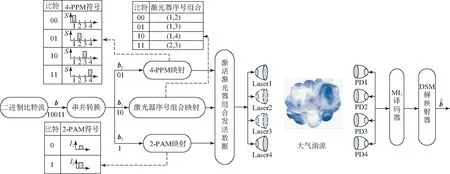
图1 双空间调制系统模型Fig.1 Model of double spatial modulation system

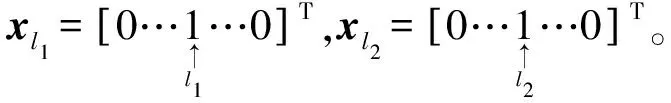
x=xl1xPPM+xl2xPAM，x∈CNt×M.

(1)

发送端发送的信号经湍流信道后由光探测器接收。设光探测器接收到的信号为：

Y=ηHx+n，Y∈CNr×M，

(2)

(3)

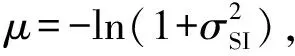
在接收端，从受到衰落和噪声干扰的输出信号中估计出原始发射符号是信号检测的关键。假设接收端已知信道状态信息，即在H已知的情况下，这里采用最大似然(Maximum Likelihood，ML)译码算法进行信号检测。ML通过穷尽搜索的方式来检测出激活激光器的序号和调制符号，能够使系统获得最优的误码性能，其准则为：

(4)

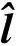
3 误码率分析

在DSM星座空间中，星座点间的距离越小，其错误检测的几率就越高，系统的误码性能就越差，即传输信号星座点间的欧氏距离是系统错误概率的决定性因素。由于DSM星座空间中的星座点是随着输入比特的不同而随机产生，所以可以通过联合界[17]技术获得DSM误码率的理论上界。

假设DSM的传输速率为m，每次发射端从2m个可能的发射信号x1，x2，…，x2m中选取一个信号进行发送。通过联合界技术可以获得采用ML检测算法时DSM系统误码率的理论上界为[17]：

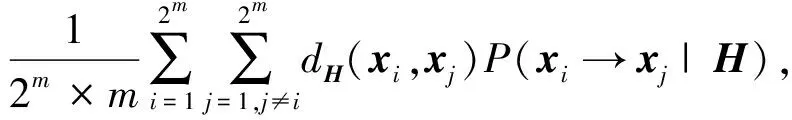
(5)

其中：dH(xi，xj)表示xi和xj之间的汉明距离，即将信号xi错误判决为xj时产生的错误比特数。P(xi→xj|H)表示接收端已知信道矩阵H时，发送符号xi被误检测为符号xj的成对错误概率，可表示为：

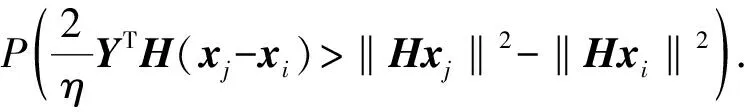
(6)

依据信道模型(2)，式(6)可表示为：

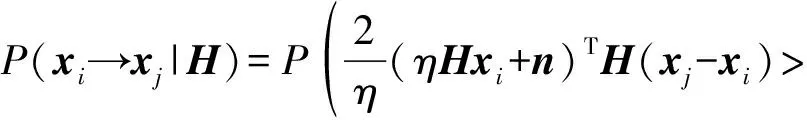
(7)

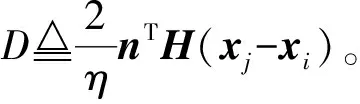
(8)

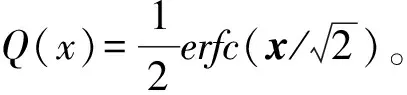
(9)

将式(9)代入式(5)可得DSM的误码率上界为：

(10)

由式(10)可得，DSM的BER不仅与汉明距离dH有关，而且与信道状态信息和传输速率有关。

4 仿真分析及结果

4.1 误码性能

图2为不同DSM系统的理论误码率和仿真误码率。其中，调制方式采用4-PPM和2-PAM。从仿真结果可以看出：随着信噪比的增加，DSM系统的误码率逐渐减小；当信噪比较低时，DSM系统的实际误码率低于理论上界；而当信噪比较大时，二者基本重合。例如，在3×4和4×4系统中，当信噪比高于23 dB时，理论分析与实际误码率曲线基本重合。增加激光器的数目可提高DSM系统的传输速率，但会带来误码性能的损失。例如，当误码率为1×10-3时，相对于(3，4)-4PPM-2PAM DSM而言，(4，4)-4PPM-2PAM DSM所需信噪比损失了2 dB，但其传输速率增加了1 bpcu。随着探测器数目的增加，DSM系统的误码性能逐渐变好，这说明系统获得了较好的接收分集增益。

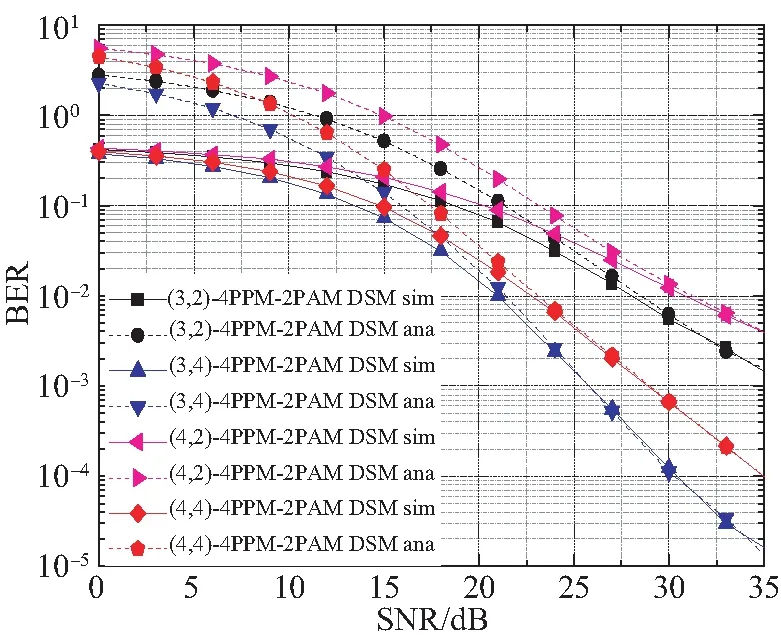
图2 不同DSM系统的理论误码率和仿真误码率Fig.2 Analytical and simulated BERs of different DSM systems

图3为不同参数下DSM方案的误码率，其中，Nr=4，传输速率为5 bpcu。从仿真结果可以看出： 当传输速率相同时，随着PPM调制阶数的增加， DSM方案的误码率逐渐减小，但会带来频谱效率的损失。例如，(3，4)-8PPM-2PAM DSM系统的误码性能最优，但其频谱效率却最低。当传输速率相同时，随着PAM调制阶数的增加，DSM系统的频谱效率逐渐增大，但系统的误码性能会恶化。例如，(3，4)-2PPM-8PAM DSM和(4，4)-2PPM-4PAM DSM的频谱效率明显优于其他DSM方案，但它们的误码性能却较差。增加激光器数目和PAM调制的阶数几乎具有相同的作用。例如，(3，4)-2PPM-8PAM DSM和(4，4)-2PPM-4PAM DSM系统、(3，4)-4PPM-4PAM DSM和(4，4)-4PPM-2PAM DSM系统，不仅具有相同的频谱效率，而且当信噪比较小时，其误码率几乎相等。

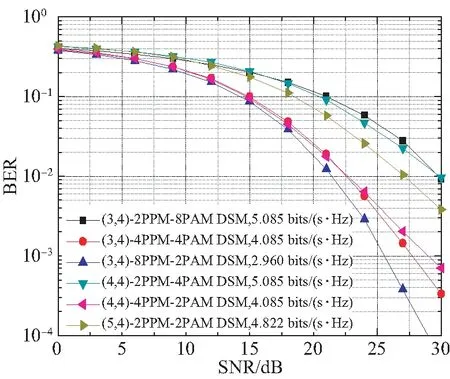
图3 传输速率为5 bpcu时不同参数下DSM的误码率Fig.3 BERs of DSM under different parameters at 5 bpcu

图4为DSM和传统OSM方案的误码率，其中，Nr=4，传输速率为5 bpcu，DSM选取图3中误码率最大和最小的系统。从仿真结果可以看出：(3，4)-8PPM-2PAM DSM系统的误码性能明显优于(4，4)-4PPM-2PAM SPPAM和(4，4)-8PAM SPAM的性能。当误码率为1×10-3时，前者相对于后两者其信噪比分别改善了约5 dB 和11 dB。相对于(4，4)-8PPM SPPM系统而言，仅当信噪比低于22 dB时，(3，4)-8PPM-2PAM DSM系统的误码率略高于前者，但其频谱效率却增加了2.335 bits/(s·Hz)。(4，4)-2PPM-4PAM DSM系统的误码性能优于(4，4)-8PAM SPAM系统，而劣于(4，4)-8PPM SPPM和(4，4)-4PPM-2PAM SPPAM系统，但其频谱效率却最高。这就说明合理地设计DSM系统，不仅可以获得较高的频谱效率和传输速率，而且其误码性能也可得到较好的改善。

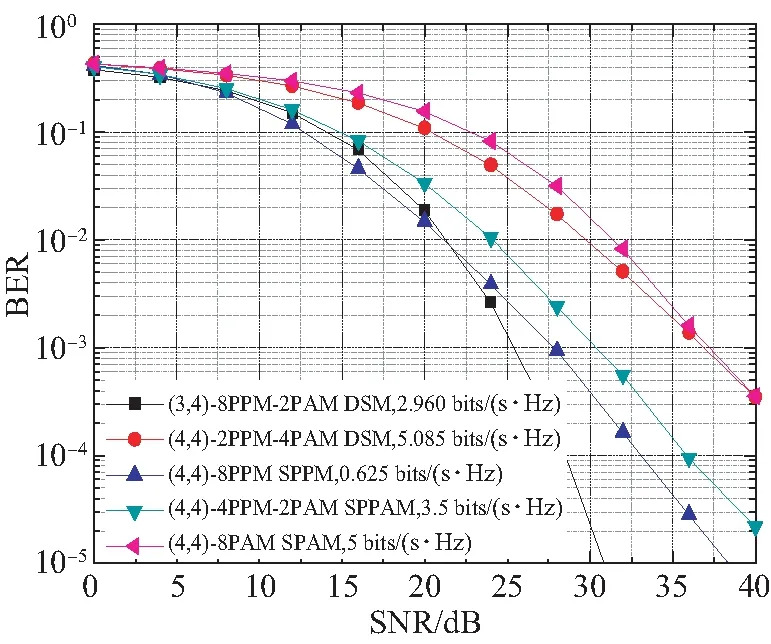
图4 传输速率为5 bpcu时DSM和传统OSM方案的误码率Fig.4 BERs of DSM and traditional OSM schemes at 5 bpcu

图5为DSM和OGSM的误码率曲线，其中，Nr=4，传输速率为5 bpcu， DSM选取图3中误码率最大和最小的系统。从仿真结果可以看出：(3，4)-8PPM-2PAM DSM系统的误码性能明显优于(3，4)-4PPM GSPPM和(3，4)-4PAM GSPAM系统的性能。当误码率为1×10-3时，前者相对于后两者其信噪比分别改善了约6 dB 和11 dB。(4，4)-2PPM-4PAM DSM系统的误码性能优于(3，4)-4PAM GSPAM系统，而劣于(3，4)-4PPM GSPPM系统，但其频谱效率相比于(3，4)-4PPM GSPPM系统提高了2.5 bits/(s·Hz)。所以在综合考虑误码性能、传输速率和频谱效率的情况下，DSM方案相比于OGSM方案更加适合于大气激光通信。

图5 传输速率为5 bpcu时DSM和OGSM的误码率Fig.5 BERs of DSM and OGSM schemes at 5 bpcu

4.2 频谱效率、传输速率及复杂度分析

为了较为全面地评价DSM方案的性能，比较了DSM和其他几种OSM方案的频谱效率、传输速率以及复杂度变化情况，其结果如表1和图6所示。从表1可以看出：DSM系统的频谱效率、传输速率以及复杂度均与激光器数和调制阶数有关，随着激光器数和调制阶数的增加，DSM系统的频谱效率、传输速率以及复杂度都会不断增加。

表1 不同OSM方案的频谱效率、传输速率和复杂度比较

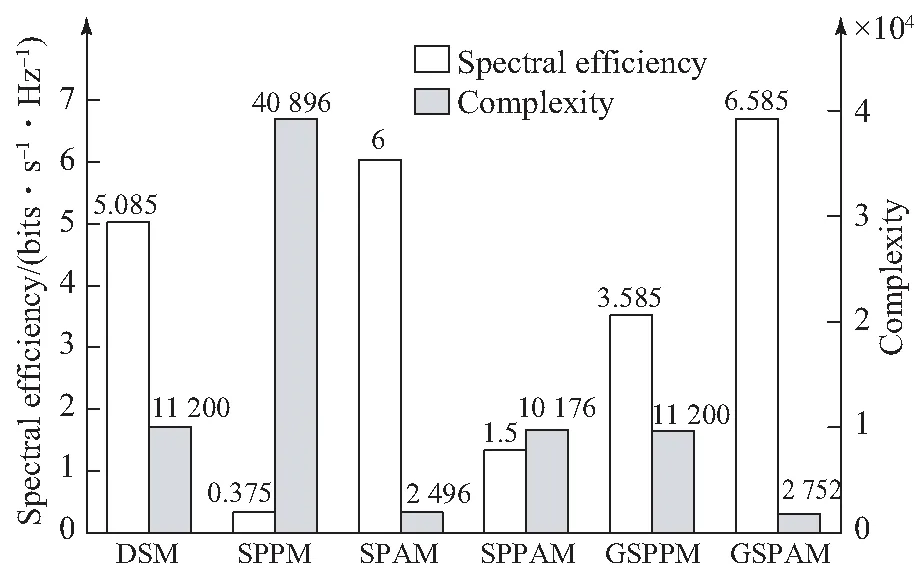
图6 传输速率为6 bpcu时不同OSM方案的频谱效率和复杂度

Fig.6 Spectral efficiency and complexity of different OSM schemes at 6 bpcu

图6为不同OSM方案的频谱效率和复杂度。其中，传输速率为6 bpcu，Nt=4，Nr=4。从图中可以看出：GSPAM方案的频谱效率最高，SPPM方案的频谱效率最低。DSM方案的频谱效率明显比SPPM，SPPAM和GSPPM方案提高了4.71，3.585和1.5 bits/(s·Hz)，而比GSPAM方案和SPAM方案降低了1.5和0.915 bits/(s·Hz)。DSM方案的频谱效率虽然略低于GSPAM和SPAM方案，但它提供了更好的误码性能。SPPM方案的复杂度最高，SPAM方案的复杂度最低。DSM方案的复杂度仅低于SPPM方案，且相对于SPPM方案降低了72.61%，相对于SPPAM方案仅增加了9.14%。虽然DSM方案的复杂度略有增加，但它却提供了更高的频谱效率和较好的误码性能，而且所增加的复杂度对现在的高速信号处理技术而言是可以接受的。因此，DSM更适合于高速率、大容量的大气激光通信。

5 结 论

针对大气激光通信对大容量、高速率的迫切需求，本文利用PPM和PAM两种调制方式，通过每次同时激活两个激光器提出了一种DSM方案，并与现有的OSM方案进行了对比。仿真结果表明：DSM方案不仅提升了系统的频谱效率和传输速率，并以少许的复杂度增加为代价，有效地改善了系统的误码性能。在相同的传输速率下，当误码率为1×10-3时，相对于(4，4)-8PPM SPPM和(3，4)-4PPM GSPPM的方案而言，(3，4)-8PPM-2PAM DSM的信噪比分别改善了约2.5 dB和6 dB，其频谱效率分别提高了2.335 bits/(s·Hz)和0.375 bits/(s·Hz)。因此，DSM作为一种新型的光空间调制方案，它充分利用空间资源实现了系统频谱效率的提升，从而大大提高了系统的数据传输速率，为未来大气激光通信传输速率的提高提供了一种有效手段。