燕尾榫约束古建木梁环境温度效应试验研究

白晓彬 杨娜 常鹏

摘   要：为了研究古建木梁在环境温度效应下顺纹方向的应变特征，在拉萨室内布置了一根无约束木梁和一根燕尾榫约束木梁，分别在室温变化下对其进行了空载和分级加载试验. 根据试验数据，分别对木材的顺纹方向弹性模量及燕尾榫的拉压刚度、转动刚度进行识别，将各参数识别成随环境温度变化的变量. 根据燕尾榫的构造特点，将升温段和降温段识别为不同的拉压刚度. 分析了上部荷载、约束条件等因素对梁底顺纹方向应变的影响，试验结果表明：无约束梁在环境温度作用下的应变增量和上部荷载无关，约束梁在环境温度作用下的应变增量随上部荷载的增大而增大. 梁端反力对梁底部的二阶弯矩作用引起了附加应变，附加应变随温度和荷载的增大而增大. 最后，根据附加应变的理论计算公式，将计算值与实测值对比，二者吻合较好，说明附加应变的理论公式是合理的.

关键词：古建木梁;环境温度作用;燕尾榫;顺纹应变;拉压刚度;附加应变

中图分类号：TU366.2                                    文献标志码：A

Experimental Analysis of Ancient Timber Beam with Dovetail

Joint Restraint under Environmental Temperature Effect

BAI Xiaobin1，2，YANG Na1？覮，Chang Peng1

（1. School of Civil Engineering，Beijing Jiaotong University，Beijing 100044，China

2. Central Research Institute of Building and Construction Co，Ltd，Beijing 100088，China）

Abstract：An unrestrained timber beam and a dovetail joint timber beam are placed in Lasa，and non-load test and step loading test are carried out，respectively，to study the strain parallel to grain of the timber beam under environmental temperature effect. According to the test data，the elasticity modulus parallel to grain of the wood，the tension and compression stiffness and rotation stiffness of the dovetail joints are identified. Considering the environmental temperature effect，the parameters are determined as variables related to the temperature variations. According to the construction features of the dovetail joint，the tension and compression stiffness in the temperature increasing stage and temperature decreasing stage are different. The influences of upper load and boundary conditions on the strain parallel to grain are analyzed. The results show that the strain variations of unrestrained beam under environmental temperature effect is unconcerned with the top load，and the strain variations of restrained beam increase along with

古建筑木結构在长期服役过程中，内部结构会出现大量的残损现象[1]，而环境温度和湿度的变化均会影响木结构的变形. 环境温度对木结构变形的影响主要体现在材料的热胀冷缩效应、弹性模量变化、边界条件的变化及由此在结构中引起的附加次应力的综合. Bai等[2]在对某古建筑的长期监测中发现，木构件的应变和温度高度相关，温度是影响结构变形的重要因素. 王阳[3]对木材的顺纹方向热膨胀系数进行了研究，认为温度变化对木材顺纹方向尺寸变化的影响不可忽略. Green等[4]根据试验提出了木材弹性模量和温度之间关系的公式，弹性模量随温度的升高而降低. Yarnold等[5]在对桥梁的长期监测研究中认为温度变化可引起结构边界条件的变化，从而影响结构的变形. 环境湿度对木结构变形的影响主要体现在木材的干缩湿胀，湿度变化会引起木材含水率的变化，从而引起木材尺寸和体积的变化[6]. 木材的干缩湿胀主要体现在横纹方向，而顺纹方向干缩湿胀相对较小[7]. 已有研究表明[8]，在拉萨地区一年之中七八月份湿度对木结构应变的影响不可忽略，而其他月份可只考虑温度作用而忽略湿度的影响. 因此本文中的试验研究避开了七八月份，用其他月份的试验数据来研究温度效应的影响.

对于静定结构，环境温度对材料所产生的热缩效应可得到释放，结构只产生应变而没有应力;对于超静定结构，由于多余约束的存在导致材料的热缩变形无法得到释放，从而产生温度应力[9]. 榫卯连接作为我国古建筑木构件之间一种常用的连接形式，具有明显的半刚性特征，属于超静定结构[10]. 榫卯节点的类型有燕尾榫、直榫、馒头榫等，而燕尾榫是应用最为广泛的一种节点，也最具代表性. 燕尾榫的榫头内窄外宽，卯口内宽外窄，抗拔性能好，使结构具有较强的整体性. 目前有关燕尾榫节点的研究大都集中在其力学性能和抗震性能方面[11-14]，对木构件环境温度作用下的变形及环境温度变化对燕尾榫刚度的影响研究较少.

本文以燕尾榫连接的古建木梁为研究对象，在拉萨室内布置了一根无约束木梁和一根燕尾榫约束梁，分别对两根梁进行了空载和分级加载试验，研究环境温度效应下木梁顺纹方向的变形特征. 根据试验数据，考虑环境温度的影响，对木材顺纹方向弹性模量、燕尾榫拉压刚度、转动刚度进行识别，分析了约束条件、上部荷载等因素对木材顺纹方向应变的影响，并对附加应变进行了理论计算.

1   试验概况

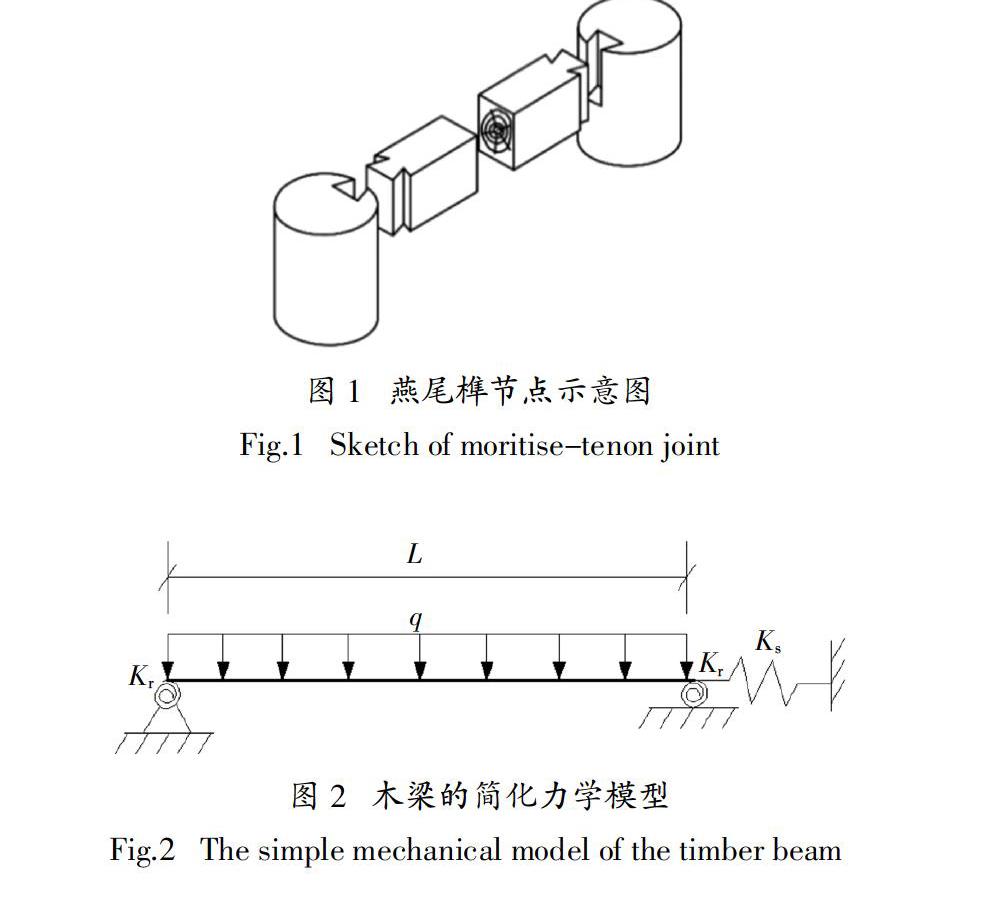
燕尾榫常用于水平构件与垂直构件的相交处，如图1 所示. 在藏式古建木结构中燕尾榫也用于梁与梁之间的连接[15]. 在荷载作用下，燕尾榫节点可以承受一定的弯矩，且具有抵抗水平推力的作用. 根据燕尾榫的构造及受力特点，可将燕尾榫连接的古建木梁简化为如图2所示力学模型. 燕尾榫的转动刚度为Kr，拉压刚度为Ks，梁承受上部均布荷载q.

试验所用木材为松木，天然干燥期5年以上. 试验地点位于拉萨，拉萨全年降水很少，全年木材平衡含水率均值较低，仅为8.6%，且起伏较小，故可认为在试验期间木材含水率保持恒定. 试验共制作两个试件，包括一个无约束的梁试件a和一个木框架试件b，如图3所示.

图3中，试件a的两端直接搁置在两个木块之上，在接触部位抹润滑油，减少接触面摩擦的影响，不施加任何额外约束;木框架试件b中的梁两端与两根短木柱以燕尾榫相连，木柱底部嵌固在木板中，将木板固定在地面上，以此来限制短柱的横向变形，为梁提供可靠的约束. 两个试件中梁的尺寸均为：b×h×l=106 mm×126 mm×975 mm.

在两根梁的底部跨中位置各安装一个光纤光栅式应变计，测量梁的顺纹方向应变;在室内布置一个光纤光栅式温度计，测量环境温度，试验的采样频率为每小时采集一次. 通过试验研究环境温度变化、边界条件和上部荷载等因素对梁底部跨中顺纹方向应变的影响.

试验分两个阶段进行，分别为空载阶段和加载阶段，试验的时间均避开了湿度影响较大的七八月份. 空载阶段的时间为2015-12-13—2016-06-30，此阶段两个试件上不施加任何荷载;加载阶段的时间为2016-09-16—2016-10-15，此阶段用红砖在两根梁上分别施加三级均布荷载，三级荷载的大小分别为q1 = 0.41 N/mm、q2 = 0.82 N/mm、q3 = 1.23 N/mm，在加载的1 h内将采样频率提高至5 次/min，待变形稳定后再降至每小时采集一次. 每级荷载的加载时间为一周，图4所示为木构架的加载情况.

2   木梁的参数识别

根据图2中的简化力学模型，木梁的未知参数包括：木材的顺纹方向弹性模量E、燕尾榫的拉压刚度Ks、转动刚度Kr. 通过试验数据和理论推导，对这些未知参数进行识别.

2.1   顺纹方向弹性模量的识别

顺纹方向的弹性模量E通过无约束梁的试验数据进行识别. 无约束梁在均布荷载下的跨中弯矩可按简支梁计算，即：M0 = ql2/8. 弯矩引起的梁底部应变为：

三次加载时刻的环境温度分别为22.2 ℃、23.6 ℃、22.9 ℃，可近似认为每次加载时的环境温度均为23 ℃. 图5为无约束梁三次加载前后的应变曲线，三次加载时应变分别增加了23.8με、25.2με、24.8με. 则每施加一级荷载应变平均增加24.6με，即q=0.41 N/mm，Δε=24.6με，由公式（2）可求得，木材在23 ℃时的弹性模量E0 =7 061.1 MPa. 根据不同时刻的环境温度值，可计算相应的弹性模量，图6为2015-12-13—2016-06-30的环境温度和弹性模量的变化曲线，二者成反比.

2.2   燕尾榫拉压刚度的识别

燕尾榫的拉压刚度Ks应用空载试验的数据进行识别. 当环境温度发生变化时，设无约束梁的应变为Δε1，约束梁的应变为Δε2，拉壓弹簧会抑制约束梁的自由变形. 以温度升高时的情况为例进行分析，当温度升高时，约束梁的位移平衡如图7所示. 图中δT为梁自由伸缩时的位移，δU为梁在约束下的实际位移，δR为约束位移，P为梁端反力. 温度升高时P为压力，温度降低时P为拉力. 约束梁的位移平衡方程为：

燕尾榫的拉压刚度Ks的大小与两根梁在空载时的应变比值有关. 对于燕尾榫而言，当温度升高时榫头和卯口为顺纹受压，温度降低时为斜纹受拉，所以升温和降温时的Ks是不同的，应分别求解升温段和降温段对应的应变比值.

根据试验数据，环境温度在1 d内可分为升温段和降温段，以2015-12-14-21：00—2015-12-15- 20：00的24个数据为例进行分析，1 d内的温度曲线、约束梁和无约束梁的应变曲线如图8所示，梁的应变和环境温度的变化趋势一致. 其中第一天21：00至第

二天9：00为降温段，共13个数据，环境温度和梁应变均逐渐减小;9：00至20：00为升温段，共12个数据，环境温度和梁应变增大. 降温段和升温段的应变数据分别分析，并将每段的第一个数据设为0，其他数据均为相对于第一个数据的应变增量，两段的应变增量数据对比如图9所示. 图9中无约束梁的应变均大于约束梁的应变，因此式（7）中的比值Δε1 /Δε2应大于1. 根据图9的应变增量计算1 d内升温段和降温段的应变比值，由于每段的第一个数据为0，故升温段可计算出11个比值，降温段计算出12个比值，1 d内的应变比值的曲线如图10所示. 依次计算每天的应变比值，并去除其中的异常比值，7个月内升温段和降温段的比值曲线如图11所示. 取其平均值，升温段应变比值为2.25，降温段应变比值为1.72. 根据式（7），可求出升温段和降温段的Ks曲线，如图12所示. 升温段的榫卯拉压刚度大于降温段，这是由于升温时卯口顺纹受压，而降温时斜纹受拉，二者受力状态不同.

2.3   燕尾榫轉动刚度的识别

燕尾榫转动刚度应用试件b的加载试验数据进行识别. 在荷载作用下，半刚性约束梁的弯矩介于铰接和固结之间，其底部跨中弯矩的公式为：M0 = aql2 （1/24

3   荷载作用下的应变分析

环境温度变化会引起木构件的伸缩变形，当梁端存在约束时，温度效应会在梁端引起支座反力. 木梁在上部荷载作用下会产生一定挠度，故支座反力会对梁底部产生二阶弯矩作用，从而引起附加应变. 本节通过试验数据对比分析约束条件、上部荷载对梁底部应变的影响.

3.1   空载段的应变分析

空载试验的时间为2015-12-13—2016-06-30. 将试验的初始应变设为0，作出约束梁和无约束梁的应变增量对比，如图15所示. 约束梁与无约束梁的应变均先减小后增加，与图6中温度增量的趋势相同，与温度增量的相关系数分别为0.7和0.8，相关性较强. 在温度变化相同的情况下，无约束梁的应变增量明显大于约束梁的应变增量，说明燕尾榫约束抑制了梁的自由变形.

3.2   荷载作用下无约束梁的应变分析

每级荷载的作用时间为一周，分析环境温度变化相同时，不同荷载对应变的影响. 分别在空载和三种荷载工况的数据中各挑选环境温度变化相似的一个循环（从第一天21：00到第二天20：00的数据为一个温度循环），并将每个循环的第一个数据设为0，得到24 h内温度增量和应变增量的对比曲线，如图16所示. 从图中可看出：当温度增量相同时，无约束梁的应变增量也基本相同，这说明上部荷载的变化对无约束梁的应变增量没有影响.

3.3   荷载作用下约束梁的应变分析

采用与无约束梁应变分析相同的方法，分析温度增量相同时，不同荷载对约束梁应变增量的影响. 约束梁的温度增量和应变增量的曲线如图17所示，由图17可看出：当温度增量相同时，约束梁的应变增量随荷载增大而增大，上部荷载引起了约束梁的附加应变. 将附加应变定义为相同温度下，约束梁有荷载时的应变增量与空载应变增量的差值. 图18所示为约束梁升温段和降温段三级荷载下的附加应变曲线. 由图18可看出，升温段和降温段的附加应变呈现相同的规律，当荷载恒定时，附加应变随温度的增大而增大;当温度恒定时，附加应变随荷载的增大而增大.

根据第2节所述的方法和图17中的实测温度增量值，可计算出约束梁一个温度循环内每一时刻的弹性模量E和转动刚度Kr，如图20所示. 由于每个荷载工况下的温度增量基本相同，因此可假定每个循环的弹性模量和转动刚度曲线一致.

将识别的参数代入式（10），可得出约束梁每级荷载下的附加应变计算值. 为对比不同边界条件对附加应变的影响，分别计算了Kr = 0、Kr = ∞时的附加应变. 图21和图22分别为降温段和升温段附加应变计算值和试验值的对比曲线. 可看出，计算值与试验值的曲线趋势一致，降温段的一级荷载、二级荷载的计算值与试验值曲线吻合较好，其余曲线计算值与试验值有些差别. 考虑到木材力学性能的离散性，且所有曲线计算值与试验值曲线均位于Kr = 0和Kr = ∞的计算值曲线之间，可以认为计算值与试验值之间的差异是可以接受的，附加应变的理论计算公式是合理的.

4   结   论

通过本文的分析，可得到以下结论：

1）通过无约束梁和燕尾榫约束梁的长期环境温度作用试验，可对其顺纹方向弹性模量、燕尾榫的拉压刚度、转动刚度等未知参数进行识别. 考虑环境温度对木材材性的影响，将各未知参数识别成随环境温度变化的变量.

2）升温和降温时燕尾榫的受力状态不同，升温段的拉压刚度大于降温段.

3）上部荷载的变化对无约束梁在环境温度作用下的顺纹方向应变没有影响.

4）约束梁在环境温度作用下的顺纹方向应变随荷载增大而增大，上部荷载引起了约束梁的附加应变，且附加应变随荷载和环境温度的增大而增大.

5）根据附加应变的理论计算公式对附加应变进行了计算，计算值与试验值的对比说明计算公式是合理的.

参考文献

[1]    周乾，杨娜，杨堃. 故宫古建木梁典型残损问题分析[J]. 水利与建筑工程学报，2016，14（3）：7—13.

ZHOU Q，YANG N，YANG K. Typical structural health problems of wooden beams of ancient buildings in the Forbidden City [J]. Journal of Water Resources and Architectural Engineering，2016，14（3）：7—13. （In Chinese）

[2]    BAI X B，YANG N，YANG Q S. Analysis of temperature effect on health monitoring data of Tibetan ancient building [C]//Proceedings of the 13th International Symposium on Structural Engineering. Beijing：Science Press，2014：1832—1836.

[3]    王阳. 殿堂式古建木构有限元分析与可靠度评估 [D]. 北京：北京交通大学土木建筑工程学院，2014：14—22.

WANG Y. Finite element analysis and reliability assessment of hall-style ancient wooden structure [D]. Beijing：School of Civil Engineering，Beijing Jiaotong University，2014：14—22. （In Chinese）

[4]    GREEN D W，EVANS J W，LOGAN J D，et al. Adjusting modulus of elasticity of lumber for changes in temperature [J]. Wood Engineering，1999，49（10）：82—94.

[5]    YARNOLD M T，MOON F L. Temperature-based structural health monitoring baseline for long-span bridges [J]. Engineering Structures，2015，86：157—167.

[6]    邱立鹏. 湿度变化和荷载作用下胶合木曲梁的工作性能研究[D]. 哈尔滨：哈尔滨工业大学土木工程学院，2015：51—67.

QIU L P. Performance of curved glulam beams under load and moisture variations [D]. Harbin：School of Civil Engineering，Harbin Institute of Technology，2015：51—67. （In Chinese）

[7]    CHAUHAN S，AGGARWAL P. Effect of moisture sorption state on transverse dimensional changes in wood [J]. European Journal of Wood and Wood Products，2004，62（1）：50—55.

[8]    白晓彬. 基于长期监测数据的西藏古建木结构温度效应研究 [D]. 北京：北京交通大学土木建筑工程学院，2018：40—44.

BAI X B. Study on temperature effect on Tibetan heritage building based on long-term monitoring data [D]. Beijing：School of Civil Engineering，Beijing Jiaotong University，2018：40—44. （In Chinese）

[9]    楊璐，尚帆，张文学. 大跨度钢结构网架温度应力及其影响分析 [J]. 空间结构，2014，20（1）：53—57.

YANG L，SHANG F，ZHANG W X. Temperature stress of large span steel truss and its influence analysis [J]. Spatial Structures，2014，20（1）：53—57. （In Chinese）

[10]  谢启芳，王龙，郑培君，等. 传统木结构单向直榫节点转动弯矩-转角关系理论分析[J]. 湖南大学学报（自然科学版），2017，44（7）：111—117.

XIE Q F，WANG L，ZHENG P J，et al. Theoretical analysis on moment-rotation relationship of straight mortise-tenon joints for Chinese traditional wooden buildings [J]. Journal of Hunan University （Natural Sciences），2017，44（7）：111—117. （In Chinese）

[11]  赵鸿铁，张海彦，薛建阳，等. 古建筑木结构燕尾榫节点刚度分析[J]. 西安建筑科技大学学报，2009，41（4）：450—454.

ZHAO H T，ZHANG H Y，XUE J Y，et al. The stiffness analysis on the characteristic of mortise-tenon joint in historical timber buildings [J]. Journal of Xi'an University of Architecture and Technology，2009，41（4）：450—454. （In Chinese）

[12]  谢启芳，杜彬，向伟，等. 古建筑木结构燕尾榫节点抗震性能及尺寸效应试验研究[J]. 建筑结构学报，2015，36（3）：112—120.

XIE Q F，DU B，XIANG W，et al. Experimental study on seismic behavior and size effect of dovetail mortise-tenon joints of ancient timber buildings [J]. Journal of Building Structures，2015，36（3）：112—120. （In Chinese）

[13]  周乾，闫维明，周锡元. 古建筑榫卯节点抗震性能试验[J]. 振动、测试与诊断，2011，31（6） ：679—684.

ZHOU Q，YAN W M，ZHOU X Y. Aseismic behavior of Chinese ancient tenon-mortise joint [J]. Journal of Vibration，Measurement and Diagnosis，2011，31（6）：679—684. （In Chinese）

[14]  康昆，乔冠峰，陈金永，等. 榫卯间缝隙对古建筑木结构燕尾榫节点承载性能影响的有限元分析[J]. 中国科技论文，2016，11（1）：38—42.

KANG K，QIAO G F，CHEN J Y，et al. The influence of gap between tenon and mortise on the bearing behavior of the dovetail joints in ancient timber structure by finite element analysis [J]. China Science Paper，2016，11（1）：38—42. （In Chinese）

[15]  李鹏.藏式古建筑木构架梁柱节点力学机理研究 [D].北京：北京交通大学土木建筑工程学院，2009：34-36.

LI P. Mechanical mechanism of beam-column joints in wooden frame of Tibetan ancient architecture [D]. Beijing：School of Civil Engineering，Beijing Jiaotong University，2009：34—36. （In Chinese）

[16]  胡习兵. T型钢半刚性连接节点的性能研究 [D]. 长沙：湖南大学土木工程学院，2004：58—61.

HU X B. The research on the behavior of T-stub semi-rigid connections [D]. Changsha：School of Civil Engineering，Hunan University，2004：58—61. （In Chinese）

[17]  白曉彬，杨娜. 长期监测中藏式古建筑木梁应变-温度模型分析[J]. 湖南大学学报（自然科学版），2017，44（11）：118—125.

BAI X B，YANG N. Strain-temperature model analysis of Tibetan ancient timber beam in long-term monitoring [J]. Journal of Hunan University （Natural Sciences），2017，44（11）：118—125. （In Chinese）

[18]  陈骥. 钢结构稳定理论与设计[M]. 北京：科学出版社，2011：75—123.

CHEN J. Stability of steel structures theory and design [M]. Beijing：Science Press，2011：75—123. （In Chinese）