间歇性强降雨下基于Green-Ampt入渗模型的边坡稳定性分析
苏永华 李诚诚

摘 要:研究了间歇性强降雨作用下边坡稳定性. 间歇性强降雨下湿润锋以上土体将会经受干湿循环作用,考虑干湿循环对边坡土体渗透特性及土水特性的影响,改进了传统Green-Ampt入渗(GA)模型;考虑干湿循环对土体强度的劣化作用,建立间歇性强降雨下边坡稳定性表达式.对于不考虑间歇性强降雨作用的边坡,改进GA模型可简化为传统GA模型,说明传统GA模型是改进GA模型的一个特例;利用改进GA模型和稳定性评价方法得到的结果与工程实际情况基本吻合,证明了该方法的可靠性;根据降雨入渗速率的变化特征,降雨过程可分为稳定阶段、持减阶段和突变阶段等3个阶段;传统GA模型与改进GA模型相比在失稳深度和时间上有较大延缓;仅改进稳定评价方法的传统GA模型与改进GA模型相比在失稳深度上一致,在失稳时间上有延缓.
关键词:间歇性强降雨;Green-Ampt入渗模型;渗透特性;土水特性;强度衰减;稳定性
中图分类号:P642.22 文献标志码:A
Slope Stability Analysis Based on Green-Ampt Infiltration
Model under Intermittent Heavy Rainfall
SU Yonghua?覮,LI Chengcheng
(College of Civil Engineering,Hunan University,Changsha 410082,China)
Abstract:The stability of slopes under intermittent heavy rainfall is studied. The soil above the wetting front is subjected to dry-wet cycles under intermittent heavy rainfall. Considering the influence of dry-wet cycles on the soil permeability and soil-water characteristics of slope,the traditional Green-Ampt infiltration (GA) model is improved. The expression of slope stability coefficient under intermittent heavy rainfall is established considering the deterioration of dry-wet cycles on soil strength. For slopes without considering intermittent heavy rainfall,the improved GA model can be simplified to the traditional GA model,which indicates that the traditional GA model is a special case of the improved GA model. The results obtained by using the improved GA model and the stability evaluation method are basically consistent with the actual engineering situation,which proves the reliability of the method. According to the variation characteristics of rainfall infiltration rate,the rainfall process can be divided into three stages: stable stage,continuous reduction stage and mutation stage. The slope infiltration depth and instability time of traditional GA are obviously behind that of the improved GA model. Compared with the improved GA model,the traditional GA model which only improves the stability evaluation method is consistent in the instability depth and delayed in the instability time.
Key words:intermittent heavy rainfall;Green-Ampt infiltration model;permeability;soil-water characteristics;strength deterioration;stability
隨着我国经济的高速发展,高陡型路堑边坡日益增多,加之极端天气多发,边坡稳定性问题日益突出.强降雨是诱发边坡失稳的最主要、最常见因素之一. 据统计,1980年以来,我国大陆所发生的大型灾害性滑坡约50%由强降雨直接触发,造成大量人员伤亡,经济损失巨大[1]. 因此,建立行之有效的强降雨作用下边坡失稳预测预报方法,对防灾减灾具有非常重要的理论意义和应用价值.
基于降雨入渗模型的边坡稳定分析是评价降雨时边坡稳定性的有效方法.基于毛细管理论提出的Green-Ampt土壤水分入渗(GA)模型[2],因其参数少、物理意义明确、精度高、适用性强、求解简单而在降雨型滑坡研究中逐渐得到应用与发展. 但传统GA模型仅适用于均质且初始含水率均匀分布的土壤水分入渗过程,因此,国内外不少学者对该模型的适用条件和范围以及主要参数的确定等问题进行了大量研究与改进,从而使该模型不断得到完善和发展. 常金源等[3]以GA模型为基础,在考虑动水压力的基础上分析了降雨入渗条件下浅层边坡稳定性.石振明等[4]提出适用于多层土边坡降雨入渗的GA模型,并采用強度折减法分析了不同降雨强度和历时下边坡稳定. Sung[5]基于初始含水率非均匀分布的GA模型提出了浅层基岩边坡稳定性分析方法. Loáiciga等[6]基于GA模型与径流波动方程建立了入渗-径流耦合模型,并探讨了该模型下的边坡稳定性. Yao等[7]提出了GA模型和分层假定下的边坡稳定性分析方法.
由于间歇性强降雨将导致坡内土体处于饱和-非饱和干湿循环过程,因此有必要用发展动态的观点研究间歇性降雨对边坡稳定性的影响.然而目前GA模型应用于边坡稳定性研究时主要考虑持续性降雨下边坡稳定性,鲜有利用GA模型研究间歇性降雨下边坡稳定性问题的报道,这限制了GA模型在边坡稳定性分析中的进一步应用.
本文首先提出一种适用于间歇性强降雨的入渗模型,该模型以 GA 模型为基础,考虑了间歇性强降雨引发的干湿循环效应对饱和层土体渗透特性及土水特性的影响;然后考虑干湿循环对土体强度的衰减作用,利用双强度折减法分析边坡稳定性;最后分析了本文模型与GA模型的关系,并通过与实际工程情况对比,验证了本文计算方法的可靠性.
1 降雨入渗模型
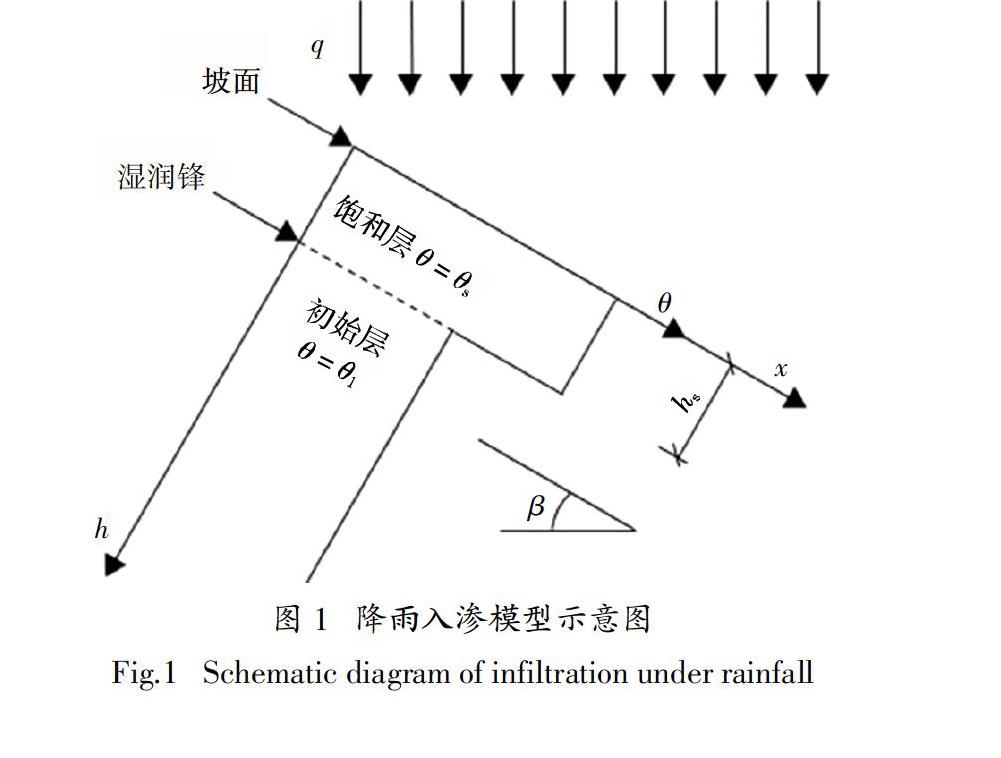
Mein等[8]将GA 模型应用到降雨入渗情况,认为降雨入渗过程应分为降雨强度控制阶段和土体入渗能力控制阶段.如图1所示,假设强降雨强度为q,饱和体积含水率为θs,初始体积含水率为θi,边坡倾角为β. 降雨初期,坡表土体处于非饱和状态,土体入渗能力大于降雨强度,降雨全部渗入土体,此时,垂直于坡面方向的降雨入渗速率为:
以每次强降雨湿润锋所达到的最大深度边界线,对土体进行分层.记第1次强降雨时湿润锋所达到的最大深度为hs,m1,第2次强降雨时湿润锋所达到的最大深度为hs,m2,第N次强降雨时湿润锋所达到的最大深度为hs,m N,则土层1的深度范围为h∈[0,hs,m1],土层2的深度范围为h∈(hs,m1,hs,m2],土层N的深度范围为h∈(h s,m(N-1),hs,m N],其余土层为初始土层,其具体分层如图3所示. 由于干湿循环由强降雨引起,故第N次强降雨时,地表土体渗透特性参数与土水特性参数采用土体经历的n次干湿循环之后相应的参数,对土层1:n = N - 1,对于土层2:n = N - 2,其余依次类推,且n ≥ 0.当n = 0时,表示该层土体为未受降雨影响的初始土层,即此次降雨前雨水入渗深度未到达该土层.
假设降雨强度控制阶段转为土体入渗能力控制阶段发生在h < hs,m1范围内,令hs,N、hsp,N和tp,N分别为第N次强降雨时湿润锋深度、临界时刻湿润锋深度和临界时刻,故第N次强降雨时土体入渗能力控制阶段的降雨入渗速率式(2)可修改为:
式(26)反映了某次强降雨下湿润锋深度随降雨历时增长的动态变化规律,考虑了间接性强降雨对边坡土体渗透特性及土水特性的影响,推广了GA模型的应用范围.
2 边坡稳定性分析
目前边坡稳定性分析方法主要有极限平衡法[12]和强度折减法[13]. 降雨入渗条件下,非饱和土边坡多发生平行于边坡表面的浅层滑坡,破坏面往往发生在湿润锋或相对隔水层处.本文以无限长边坡体为研究对象,假定湿润锋以上土体处于饱和状态,并以湿润锋处作为潜在滑动面,在考虑干湿循环对土体力学特性的衰减作用下,利用双强度折减法评价边坡稳定性随强降雨湿润锋深度、强降雨次数的动态变化过程,其计算简图如图4所示.
3 模型验证与分析
3.1 与传统GA模型解析解比较
传统GA模型不考虑间歇性降雨对边坡土体渗透特性及土水特性的影响,即令改进GA模型强降雨次数N = 1,则式(26)可化简为:
3.2 案例计算与分析
广西百隆路某段右侧高10 m、坡率1 ∶ 1.5的新修路堑边坡在经历第1个雨季时发生浅层坍滑.土体设计参数见表1.土体土水特征曲线函数表达式、有效黏聚力c′、有效内摩擦角φ′和孔隙比与干湿循环次数n满足的函数关系分别如式(35)~(39)所示.假设当地平均气温25 ℃,每次强降雨历时为4 h,降雨强度 q = 0.000 8 cm/s.
不同干湿循环次数下,土体脱湿曲线和吸湿曲线的偏移系数见表2.图5所示为n = 0和n = 10土水特征曲线.同文献[11]所反映的规律相同,该土体不同干湿循环下土水特征曲线均存在明显的滞后现象,且随着干湿循环次数的增加,滞回效应明显减小,并趋于稳定;若干次干湿循环后土体土水特征曲线中脱湿曲线的偏移量大于吸湿曲线的偏移量.
图6所示为不同干湿循环次数下,土体吸湿过程湿润锋处基质吸力与土层饱和导水率变化曲线.可知,土体吸湿时湿润锋处基质吸力随着干湿循环次数的增加而减小,且首次循环降幅最大,多次循环后趋于稳定.饱和导水率随着干湿循环次数的增加而增大,但增大速率逐渐放缓.土体吸湿时湿润锋处基质吸力和饱和导水率的变化皆表明了随着干湿循环次数的增加,土体逐渐松散,土体持水能力逐渐降低,符合相关试验研究和自然条件下土体实际渗流特性[18].
根据降雨入渗速率的变化特征,将降雨过程分为稳定阶段、持减阶段和突变阶段等3个阶段,如图7所示. 但当N = 1时,只有稳定阶段、持减阶段2个阶段;不同降雨次数下每个阶段开始时间和持续时间也并不相同.
阶段的入渗速率与强降雨次数无关,保持为qcos β.某次降雨下,该阶段湿润锋深度与降雨历时呈正比,边坡稳定性系数随降雨历时的增长快速下降.不同强降雨次数下,该阶段持续时间随强降雨次数的增加而增加,其原因在于干湿循环过程中,饱和导水率的变化占主导位置,浅层土体入渗能力随干湿循环次数的增加而增强;边坡稳定性系数随强降雨次数的增加而减小,其原因在于干湿循环降低了土体的抗剪强度.
持減阶段是指降雨入渗速率随降雨历时的增长连续稳定下降阶段.假定第一次降雨时其湿润锋所达到的最大深度为hs,m1,某次降雨下(N > 1),湿润锋到达hs,m1深度的降雨历时为ts,m N,该阶段的持续时间段为tp,N ~ ts,m N;湿润锋深度随降雨历时的增加而增加,但增加速度逐渐变慢;边坡稳定性系数随降雨历时的增长而下降,但下降速度亦逐渐放缓.不同强降雨次数下,该阶段的持续时间随强降雨次数的增加而减小,其原因在于干湿循环效应使得土层饱和导水率不断增大,而基质吸力变化并不明显,故上层土层内的渗透速率增大,降雨穿越上层土层的时间变短,而且随着强降雨次数的增加,浅层土体会更多地按雨强控制阶段的入渗速率进行渗透;该阶段的入渗速率、湿润锋深度随强降雨次数的增加而增加;边坡稳定性系数随强降雨次数的增加而减小.
突变阶段是指ts,m N至降雨结束阶段.该阶段的入渗速率呈阶梯式突变,其原因在于不同土层土体所经历的干湿循环次数并不相同,土体埋深越深其经历的干湿循环次数就越少,其饱和导水率小于上层土体,基质吸力大于上层土体,但本案例中饱和导水率的变化占主导地位,故其入渗速率会在土层接触面发生向下突变.某次降雨下,突变点之间的入渗速率逐渐降低;湿润锋深度随降雨历时增加而增加,但增加速率减缓较快;边坡稳定性系数随降雨历时的增大而减小,但在土层接触面发生突变而变大,其原因在于深部土体所受干湿循环较少,土体抗剪强度随深度逐渐提高.不同强降雨次数下,入渗速率的降低速率随强降雨次数的增加而增大,该阶段结束时刻,降雨次数越多,入渗速率越小,其原因在于强降雨下湿润锋最终达到的深度会逐渐增加,且其土层为原状土体,其饱和导水率与基质吸力相同,但深度加深;湿润锋深度随强降雨次数的增加而增加;边坡稳定性系数随强降雨次数的增加而减小.
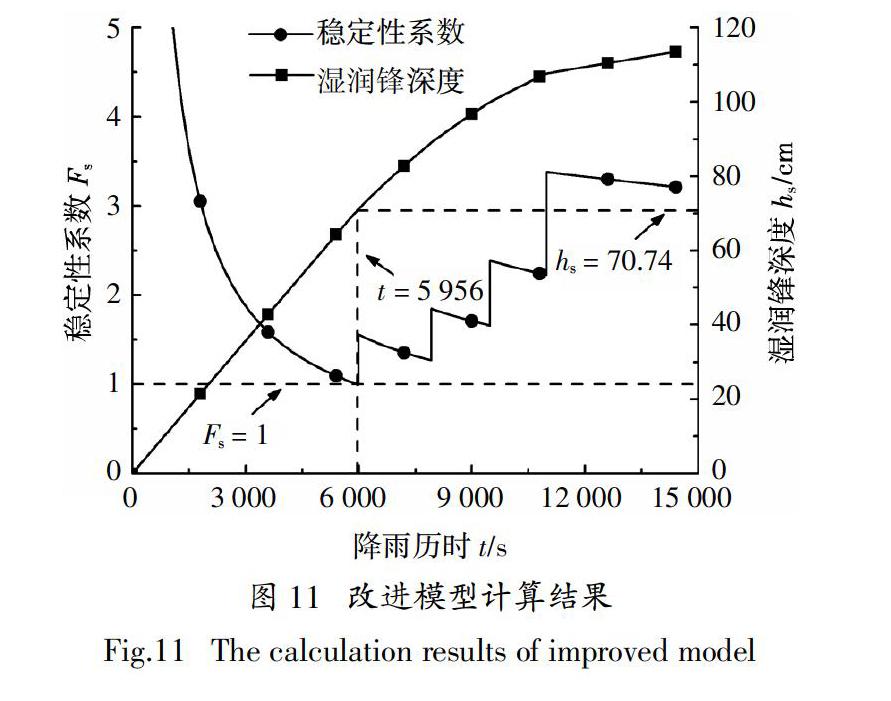
如图11所示,本文模型边坡失稳时,降雨次数N=5,降雨历时t=5 956 s,滑动面埋深hs=70.74 cm,说明边坡在前4次强降雨下能保持稳定,但间歇性降雨引发的干湿循环效应导致土体土水保持能力和强度降低,稳定性系数越来越小,第5次强降雨时发生浅层滑坡,这与广西百隆路修建过程中的边坡实际破坏情况基本吻合[19-20],证实本文方法的可靠性.
一般而言,边坡稳定性系数不会随着降雨历时的增加而增加,故本文方法下边坡稳定性系数应取整个降雨过程稳定性系数的最小值. 由图12可知,不同强降雨次数下,边坡稳定性系数的最小值皆出现在第二土层内,解释了降雨条件下非饱和土质边坡多发生浅层破坏的原因.本文方法同时考虑了干湿循环作用下边坡土体风化层逐步加深和土体强度的逐步衰减,说明了本文方法的全面性.同时,由以上分析可知,初始状态下均质土边坡在经历若干次降雨后将变成多层非均质土坡,边坡土体渗透特性参数、土水特征参数及强度参数非均匀分布,且表现为沿深度方向发生变化,此变化过程及变化结果符合实际情况,从侧面证明了本文所提模型的合理性.
3.3 不同模型对比
仍以上述案例为例,分别以传统GA模型+极限平衡法、传统GA模型+双强度折减法、改进GA模型+双强度折减法3种模型计算边坡失稳时间及失稳深度.每次计算中降雨强度相同,传统GA模型+极限平衡法的降雨历时为5 × 104 s,其余模型每次降雨历时为5 × 104 s除以对应降雨次数. 其计算结果如表3所示,其中计算模型一、二、三分别与传统GA模型+极限平衡法、传统GA模型+双强度折减法和改进GA模型+双强度折减法相对应,表中计算结果(1,400 093,400)含义:1表示边坡失稳时的降雨次数N=1,400 093表示失稳时的降雨历时t=400 093 s,400表示失稳时湿润锋深度h = 400 cm.
由表3可知,相同降雨量下,持续性降雨诱发边坡失稳的时间和滑坡体量远大于间歇性降雨的结果,这在某种程度上证实了“大雨大滑,小雨小滑”. 仅利用GA模型结合极限平衡法评价强降雨下边坡的稳定性,而忽略前期间歇性强降雨的影响会使预测结果在时间和深度上有较大延迟,进而导致边坡失稳得不到及时有效的预测,并且在防治时造成不必要的资源浪费.因此降雨入渗时,有必要考虑间歇性强降雨作用,改进模型更有利于准确预测入渗深度与边坡稳定性分析.模型二与模型三相比在失稳的深度、体量上基本相同,但模型二在失稳时间上有较大延迟,两种模型所预测边坡失稳的时间和深度皆随降雨次数的增加而减小.模型三考虑了间歇性降雨对土体渗透特性、土水特性和土体强度的影响,相比于前人研究成果更加符合实际.
4 讨 论
1)本文所提模型的入渗速率和稳定性系数存在突变阶段的根本原因在于GA模型假定湿润锋面至坡面间的土体体积含水率为饱和含水率,间歇性强降雨作用下湿润锋面面上面下土体所经历的干湿循环次数不同,故在每次强降雨湿润锋所达到的最大深度附近土体在渗透特性和土水特性有较大不同,进而产生突变.事实上,湿润锋面至坡面间土体并非完全饱和,而是存在饱和层、非饱和过渡区、传导层等[21].间歇性降雨下基于分层假定的边坡稳定性分析有待进一步研究.
2)土体入渗能力随强降雨次数增长而变化的过程中,饱和导水率的变化或基质吸力的变化占主导地位将对降雨入渗速率、湿润锋深度等随降雨历时、干湿循环次数变化而变化的物理量产生不同的影响,限于篇幅本文不再分析,具体影响可结合工程实例具体分析,分析方法同本文所提案例分析方法相同.
3)本文对前人优秀研究成果加以综合利用,以
提供一种可用于间歇性强降雨下边坡降雨入渗计算及边坡稳定性分析方法.为使论文在表达上简洁有效,在公式推导过程中用函数关系表达孔隙比、土体强度参数随干湿循环次数变化规律.这种函数关系是真实存在的,只是函数表达式不一定是连续函数,在实际工程或试验中此函数更可能符合离散函数,利用本文方法进行间歇性强降雨入渗及边坡稳定性分析时,可利用工程或试验实测结果进行计算.
5 结 论
1)基于传统GA模型,本文推导了间歇性强降雨下考虑土体渗透特性及土水特性变化的退化GA模型,根据降雨入渗速率的特征,将降雨历程划分为稳定阶段、持减阶段、突变阶段,并有机结合极限平衡法和强度折减法进行边坡稳定性分析.
2)某次降雨下,湿润锋深度随降雨历时的增长持续向下发展,但发展速率逐渐放缓;同一降雨历时下,湿润锋深度随着强降雨次数的增加而增长,增长速率亦逐渐放缓.
3)某次降雨下随降雨历时的增加,稳定阶段、持减阶段边坡稳定性系数逐渐减小,突变阶段边坡稳定性系数发生向上突变而增大;随着强降雨次数的增加,边坡稳定性系数逐渐减小.
4)利用传统GA模型结合极限平衡法评价边坡稳定性时在失稳深度和时间上有较大延缓;传统GA模型结合双强度折减法评价边坡稳定性时能很好地反映失稳深度,但在失稳时间上有较大延迟;改进GA模型结合双强度折减法,既考虑了干湿循环对土体渗透特性和土水特性的影响,又考虑了其对土体抗剪强度的衰减作用,更加符合实际.
参考文献
[1] 黄润秋. 20世纪以来中國的大型滑坡及其发生机制[J].岩石力学与工程学报,2007,26(3):433—454.
HUANG R Q. Large-scale landslides and their sliding mechanisms in China since the 20th century[J]. Chinese Journal of Rock Mechanics and Engineering,2007,26(3):433—454. (In Chinese)
[2] HEBER G W,AMPT G A . Studies on soil physics [J]. The Journal of Agricultural Science,1911,4(1):1—24.
[3] 常金源,包含,伍法权,等. 降雨条件下浅层滑坡稳定性探讨[J]. 岩土力学,2015,36(4):995—1001.
CHANG J Y,BAO H,WU F Q,et al. Discussion on stability of shallow landslide under rainfall [J]. Rock and Soil Mechanics,2015,36(4):995—1001. (In Chinese)
[4] 石振明,沈丹祎,彭铭,等. 考虑多层非饱和土降雨入渗的边坡稳定性分析[J]. 水利学报,2016,47(8):977—985.
SHI Z M,SHEN D Y,PENG M,et al. Slope stability analysis by considering rainfall infiltration in multi-layered unsaturated soils [J]. Journal of Hydraulic Engineering,2016,47(8):977—985. (In Chinese)
[5] SUNG E C. Prediction of shallow landslide by surficial stability analysis considering rainfall infiltration [J]. Engineering Geology,2017,231:126—138.
[6] LO?魣ICIGA H A,JOHNSON J M. Infiltration on sloping terrain and its role on runoff generation and slope stability [J]. Journal of Hydrology,2018,561:584—597.
[7] YAO W M,LI C D,ZHAN H B,et al. Time-dependent slope stability during intense rainfall with stratified soil water content [J]. Bulletin of Engineering Geology and the Environment,2019,2:1—15.
[8] MEIN R G,LARSON C L . Modeling infiltration during a steady rain [J]. Water Resources Research,1973,9(2):384—394.
[9] 江强强,刘路路,焦玉勇,等. 干湿循环下滑带土强度特性与微观结构[J]. 岩土力学,2019,40(3):1005—1012+1022.
JIANG Q Q,LIU L L,JIAO Y Y,et al. Strength properties and microstructure characteristics of slip zone soil under wetting-drying cycles [J]. Rock and Soil Mechanics,2019,40(3):1005—1012+1022. (In Chinese)
[10] 劉昌鑫,潘健,邓羽松,等. 干湿循环对崩岗土体稳定性的影响 [J]. 水土保持学报,2016,30(6):253—258.
LIU C X,PAN J,DENG Y S,et al. The influence of wet-dry cycles on collapsing gully soil stability [J]. Bulletin of Soil and Water Conservation,2016,30(6):253—258. (In Chinese)
[11] 张俊然,许强,孙德安. 多次干湿循环后土-水特征曲线的模拟[J]. 岩土力学,2014,35(3):689—695.
ZHANG J R,XU Q,SUN D A. Simulation of soil-water characteristic curves during drying and wetting cycles [J]. Rock and Soil Mechanics,2014,35(3):689—695. (In Chinese)
[12] 陈昌富,杨宇. 边坡稳定性分析水平条分法及其进化计算[J].湖南大学学报(自然科学版),2004,31(3):72—75.
CHEN C F,YANG Y. Horizontal slice method of slope stability analysis based on evolutionary algorithm [J]. Journal of Hunan University (Natural Sciences),2004,31(3):72—75. (In Chinese)
[13] 苏永华,张航,蹇宜霖. 基于滑带刚度退化的古滑坡自稳能力研究[J]. 湖南大学学报(自然科学版),2018,45(7):77—84.
SU Y H,ZHANG H,JIAN Y L. Research on self stabilizing ability of ancient landslide based on stiffness degradation of sliding zone [J]. Journal of Hunan University (Natural Sciences),2018,45(7):77—84. (In Chinese)
[14] 涂义亮,刘新荣,钟祖良,等. 干湿循环下粉质黏土强度及变形特性试验研究[J].岩土力学,2017,38(12):3581—3589.
TU Y L,LIU X R,ZHONG Z L,et al. Experimental study on strength and deformation characteristics of silty clay during wetting-drying cycles [J]. Rock and Soil Mechanics,2017,38(12):3581—3589.(In Chinese)
[15] CHEN L ,YOUNG M H . Green-Ampt infiltration model for sloping surfaces [J]. Water Resources Research,2006,42(7):1—9.
[16] 党发宁,刘海伟,王学武,等. 基于有效孔隙比的黏性土渗透系数经验公式研究[J]. 岩石力学与工程学报,2015,34(9):1909—1917.
DANG F N,LIU H W,WANG X W,et al. Empirical formulas of permeability of clay based on effective pore ratio [J]. Chinese Journal of Rock Mechanics and Engineering,2015,34(9):1909—1917. (In Chinese)
[17] SL237—1999 土工试验规程[S].北京:中国水利水电出版社,1999:68—69.
SL237—1999 Specification of soil test [S]. Beijing:China Water Power Press,1999:68—69. (In Chinese)
[18] 孙德安,黄丁俊. 干湿循环下南阳膨胀土的土水和变形特性[J].岩土力学,2015,36(S1):115—119.
SUN D A,HUANG D J. Soil-water and deformation characteristics of Nanyang expansive soil after wetting-drying cycles [J]. Rock and Soil Mechanics,2015,36(S1):115—119. (In Chinese)
[19] 杨和平,肖杰,程斌,等. 开挖膨胀土边坡坍滑的演化规律[J]. 公路交通科技,2013,30(7):18—24.
YANG H P,XIAO J,CHENG B,et al. Landslide evolution regularity of excavated expansive soil slope [J]. Journal of Highway and Transportation Research and Development,2013,30(7):18—24. (In Chinese)
[20] 王兴正.模拟干湿循环及低应力条件的膨胀土抗剪强度试验研究[D]. 长沙:长沙理工大学交通运输工程学院,2014:45—47.
WANG X Z. The research of shear strength tests of expansive soil with dry-wet cycle simulation and lower stress condition [D].Changsha:School of Traffic & Transportation Engineering,Changsha University of Science & Technology,2014:45—47. (In Chinese)
[21] BODMAN G B,COLMAN E A. Moisture and energy conditions during downward entry of water into soils[J]. Soil Science Society of America Journal,1944,8(2):166—182.

