基于趋势变化分段的电力负荷组合预测方法

谭风雷， 张 军， 马宏忠

(1.国网江苏省电力有限公司检修分公司，江苏 南京 211102； 2.河海大学 能源与电气学院，江苏 南京 211100)

0 引 言

随着我国用电量逐年增加，为了满足社会经济的快速增长，电力事业得以空前发展，电力系统逐渐建成了“以特高压电网为骨干网架，各级电网协调发展的坚强电网”[1-2]。随着全社会大量电能的需求，电力负荷预测变得格外重要，是我国电力企业(国家电网有限公司和中国南方电网有限责任公司)的重要工作之一，准确的负荷预测，能够合理安排电力系统发电机组的启停和输变电设备检修计划，在满足社会用电需求的同时，减少不必要的电能浪费，降低发电成本，提高经济社会效益，已成为衡量电力企业管理走向现代化的显著标志，尤其在用电管理走向市场的情况下，电力负荷预测变得更加重要[3]。

电力负荷预测是一门涉及数学分析、经济增长、人文科学等的综合学科，其受到诸多因素的影响，主要包括地域、环境、时间、经济、政治等因素，由于进行电力负荷预测时，难以综合考虑到多种因素，使得电力负荷预测精度不易提高，这样研究一种简单且精度较高的电力负荷预测方法就成为了诸多专家学者的研究重点。目前，针对电力负荷预测的方法有很多，也比较成熟，主要集中在多元线性回归法、时间序列法、BP神经网络、灰色理论等方法[4-6]。文献[7]提出了一种基于温湿度因子的多元线性回归法，并基于积温效益对温度因子进行了修正，提高了算法的准确性。文献[8]提出了一种基于支持向量机的电力负荷预测方法，该方法基于最小二乘法的思想计算得到了支持向量机的最优参数，最后通过算例表明该方法运算速度快，预测精度高。文献[9]提出了一种基于指数平滑法预测电力负荷的方法，该方法基于模糊理论对天气状况进行了量化处理，并修正了模型参数，有效提高了预测精度。上述文献大多未考虑电力负荷变化曲线存在“三峰三谷”[10-11]变化特性，且使用的预测方法较为单一。实际上，由于电力负荷变化曲线存在“三峰三谷”变化特性，使得各时段变化趋势不同，只有各时段单独考虑，单独使用预测方法才能提高预测精度。另外，预测方法单一时，必然存在一定缺陷，可利用加权组合思想[12-14]，充分结合各种预测方法的优点，提高算法优势。基于上述分析可知，为进一步提高电力负荷预测精度，需充分考虑电力负荷变化曲线的“三峰三谷”变化特性和加权组合预测思想。

针对上述问题，本文以苏北某地区的历史电力负荷数据作为研究对象，分析该地区电力负荷“三峰三谷”变化特性，并基于连续性原理，按照趋势变化将电力负荷变化曲线划分为6个时间段。同时基于加权组合的思想，每个时间段均采用线性回归法、趋势变化法、BP神经网络和支持向量机的加权组合预测方式，借助最小二乘法的思想，求解得到组合预测模型的最优参数。最后借助实际算例验证了该算法的可行性。

1 电力负荷变化趋势分析与时段划分

1.1 基于电力负荷平均变化率的时段划分方法

电力负荷存在区域性、时间性等特性，不同地域不同时间对应的电力负荷变化趋势各不相同，本文以苏北某地区夏季50个工作日对应的电力负荷数据作为研究对象，首先来分析电力负荷变化趋势。

图1为该地区典型日电力负荷曲线，显然该地区电力负荷变化曲线呈现三个峰值和三个谷值，一般称作“三峰三谷”现象，所谓“三峰”是指早高峰、午高峰和晚高峰，而“三谷”是指早低谷、午低谷和晚低谷。

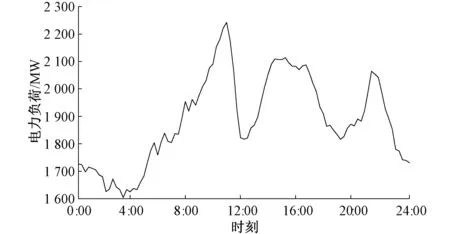
图1 典型日电力负荷曲线Fig.1 Typical daily power load

由于典型日电力负荷曲线存在独特性，不能完全代表该地区电力负荷曲线，因此在分析“三峰三谷”现象时，文中又绘制了该地区平均电力负荷变化曲线如图2所示。显然，平均电力负荷曲线仍然存在“三峰三谷”现象，其中早高峰时间为10时45分，午高峰时间为14时45分，晚高峰时间为21时15分，三个高峰时间均为上班用电、居民用电的高峰时期；早低谷时间为3时45分，午低谷时间为12时，晚低谷时间为18时45分， 三个低谷时间均为休息用电的低谷时期，与社会实际用电情况相符。

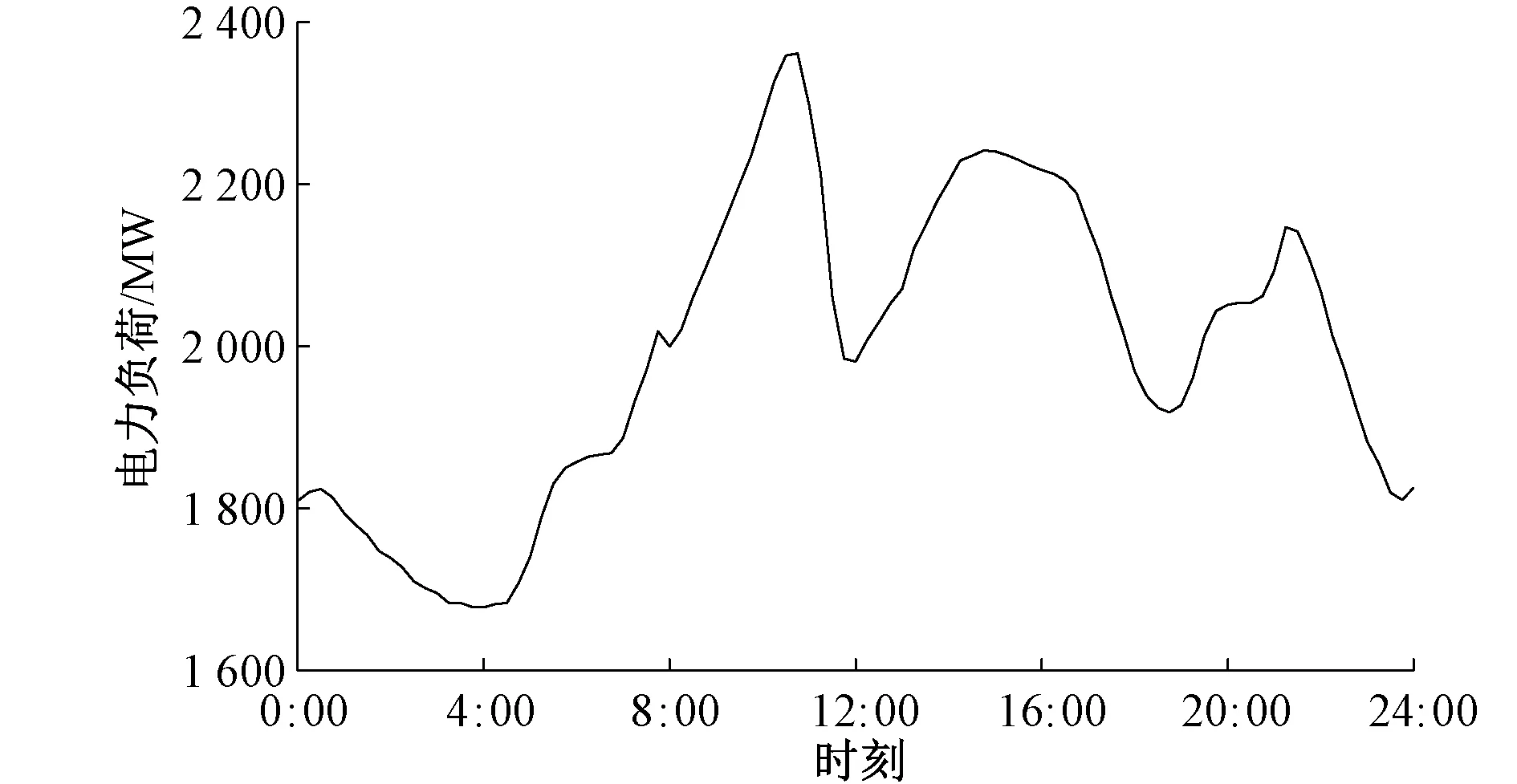
图2 平均电力负荷曲线Fig.2 Average power load

根据电力负荷的“三峰三谷”特性，则电力负荷曲线就可以分为6个时间段。“三峰三谷”时刻确定后，现利用电力负荷变化率曲线(如图3所示)来确定“三峰三谷”对应的时间段。

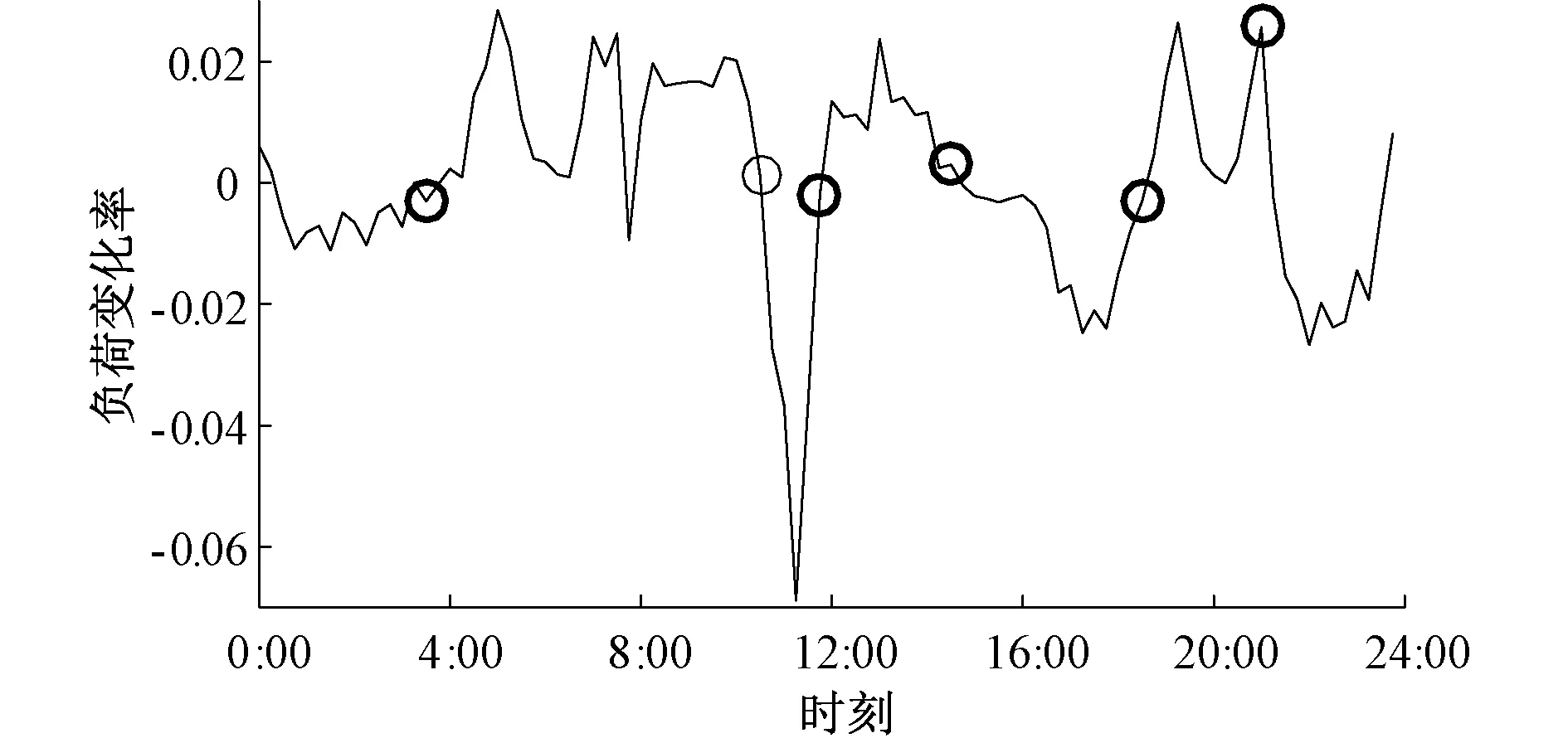
图3 电力负荷变化率曲线Fig.3 Change rate of power load

文中假设“三峰三谷”对应的时间段确认原则如下：

(1)任意时间段内电力负荷变化率应遵循连续性原理，不存在较大阶跃值；

(2)原则上任意时间段内电力负荷变化率连续波动有且只有1次，其中最大电力负荷变化率与最小电力负荷变化率之差应大于0.05；

(3)如果任意时间段内电力负荷变化率连续出现2次及以上波动时，其最大电力负荷变化率与最小电力负荷变化率之差可以不大于0.05。

基于上述三个原则，“三峰三谷”对应的时间段划分情况如表1所示：

表1 “三峰三谷”对应的时间段划分情况

1.2 基于K-means聚类的时段划分方法

考虑到基于电力负荷平均变化率的时段划分方法是基于平均电力负荷曲线，未充分考虑各样本的特点，使得时段划分不够准确，因此本文采用了基于K-means聚类的时段划分方法[15]，具体步骤如下：

步骤1：选择苏北某地区夏季50个工作日的电力负荷数据作为样本集，设聚类数为2，迭代次数为R。

步骤2：选取日峰负荷和日谷负荷作为原始聚类中心Cij，式中i=1、2，j=1、2、3…R。

步骤3：计算各时刻电力负荷与原始聚类中心的距离Dk，表达式如下：

Dk=(Lk-Cij)2

(1)

式中：Lk表示某日第k时刻的电力负荷值。

步骤4：计算新的聚类中心，表达式如下：

(2)

式中：Nij表示第i种聚类第j次迭代后所包含的样本点数；Lij表示第i种聚类第j次迭代后所对应的样本点负荷。

步骤5：每次迭代后，构造误差平方和准则函数，表达式如下：

(3)

当第j次迭代后Jj取得最小值，这时对应的聚类结果即为最优结果，根据此结果就可以进行“三峰三谷”划分，否则重新进行迭代。

步骤6：对50个样本都采用K-means聚类，统计出96个时刻分别被划分到6个时段的天数。

步骤7：利用最大天数原则，当某时刻被划分到某时段的天数最大，此时刻就属于此时段。

基于K-means聚类原理，本文对“三峰三谷”时段划分情况进行了修正，结果如表2所示。

表2 “三峰三谷”时段划分修正结果

Tab.2 Correction results for the time division of “three peaks and three valleys”

“三峰”早高峰午高峰晚高峰时间段09:30-11:4513:15-18:0020:30-22:00“三谷”早低谷午低谷晚低谷时间段22:00-09:3011:45-13:1518:00-20:30

2 基于趋势变化分段的电力负荷预测方法

根据“三峰三谷”变化趋势可知，电力负荷曲线可以划分为6个时间段，每个时间段所对应的变化趋势不同，若每个时间段都采用相同的预测方法，必然影响到预测精度，因此本文考虑在不同时段应用不同的预测方法来提高预测精度。

目前，电力负荷预测方法有很多，主要包括线性回归法、趋势变化法、时间序列法、BP神经网络、支持向量机(SVM)和模糊理论等方法[16-17]，本文主要研究线性回归法、趋势变化法、神经网络及SVM四种常用的电力负荷预测方法，以苏北某地区夏季前40个工作日对应的电力负荷数据作为历史负荷数据(如图4所示)，后10个工作日对应的电力负荷数据作为预测负荷数据。

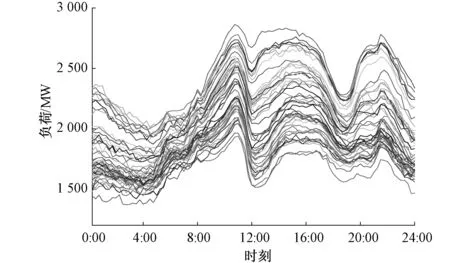
图4 历史负荷曲线Fig.4 Historical load

分析线性回归法、神经网络和支持向量机前，先研究电力负荷的影响因素，针对夏季负荷，文中重点研究电力负荷与温湿度与的相关性，如图5和6所示，显然电力负荷与温湿度具有一定相关性，与温度呈正相关，与湿度呈负相关。因此文中研究线性回归法、神经网络和支持向量机时，主要考虑基于环境温度与湿度因子，而趋势变化预测法是基于负荷趋势变化因子。

图5 负荷与温度相关性Fig.5 Correlation of load and temperature

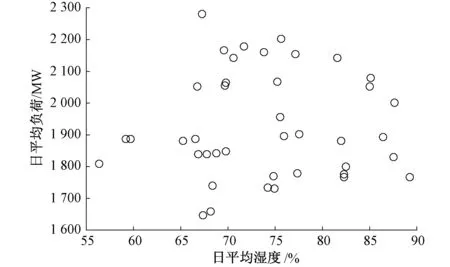
图6 负荷与湿度相关性Fig.6 Correlation of load and humidity

基于上述四种方法的预测结果如表3所示，其中线性回归法简称为MR，趋势变化预测法简称为MT，BP神经网络预测法简称为MB，支持向量机预测法简称为MS。其中采用BP神经网络预测法和支持向量机预测法预测电力负荷时，需对电力负荷和温湿度因子进行归一化处理[18]，处理原则为

(4)

式中：Li(t)表示第i天t时刻对应的电力负荷、温湿度因子实际值；Lmaxt表示第t时刻对应的电力负荷、温湿度因子最大值；Lmint表示第t时刻对应的电力负荷、温湿度因子最小值；L1i(t)表示第i天t时刻对应的电力负荷、温湿度因子归一化值；C表示归一化系数，当对电力负荷归一化处理时，C取值为100 MW，当对温度归一化处理时，C取值为1 ℃，当对湿度归一化处理时，C取值为10%。

针对BP神经网络预测法，训练函数设置为“trainlm”，神经元2层，第一层设置6个神经元，传递函数设置为“purelin”，第二层设置1个神经元，传递函数设置为“tansig”，最大训练次数设置为3 000，训练要求精度设置为0.001，学习率设置为0.000 1，最小梯度要求设置为1e-12，u的初始值设置为1e-12；针对支持向量机预测法，核函数设置为“linear”，损失函数设置为“einsensitive”。

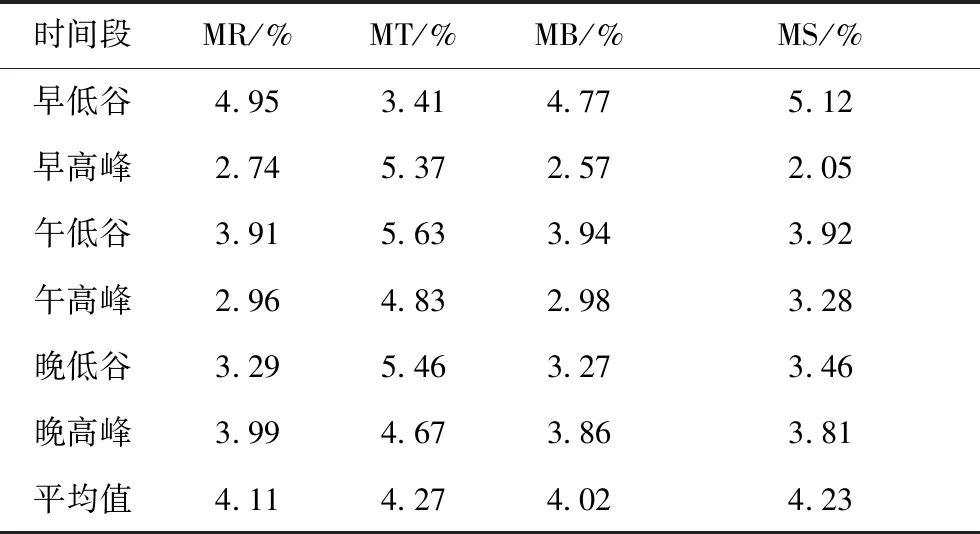
表3 四种方法的预测结果

分析表3可知：早低谷时段，趋势变化预测法(MT)预测精度最高；早高峰时段，支持向量机预测法(MS)预测精度最高；午低谷时段，线性回归法(MR)预测精度最高；午高峰时段，线性回归法(MR)预测精度最高；晚低谷时段，BP神经网络预测法(MB)预测精度最高；晚高峰时段，支持向量机预测法(MS)预测精度最高。若每个时段均采用预测精度较高的方法，预测精度必然得以提高，则基于趋势变化分段的电力负荷预测方法为MR、MT、MB和MS的组合预测方法，其六个时段对应的方法如表4所示。

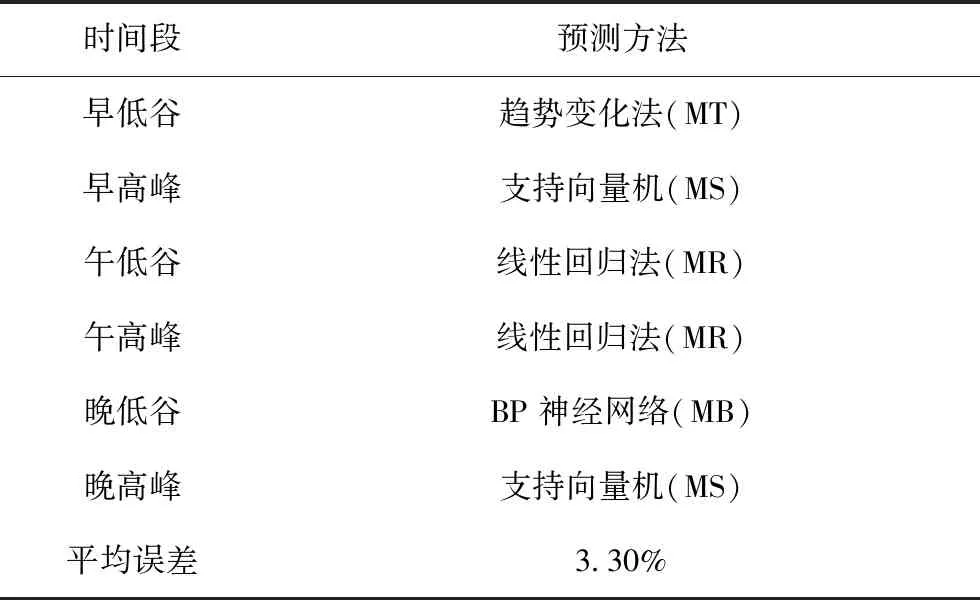
表4 六个时段对应的预测方法

分析表4可知：采用基于趋势变化分段的电力负荷预测方法，综合了MR、MT、MB和MS四种预测方法的优势，使得平均相对误差降低至3.30%，预测精度得以大幅度提高。

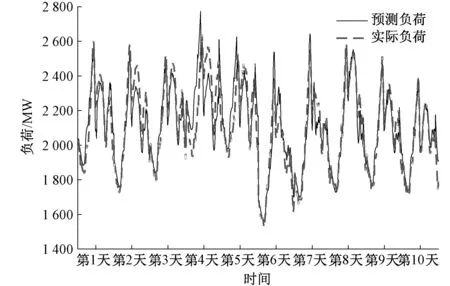
图7 整体预测效果Fig.7 Overall prediction and actual load

为了进一步分析预测效果，又绘制了整体预测效果(图7)和10个工作日的相对误差图(图8)，显然采用基于趋势变化分段的电力负荷预测方法后，最大相对误差为7.54%，最小相对误差为1.89%，相对误差小于等于3%的天数为5个，占比50%，相对误差小于等于5%的天数为9个，占比90%，可见该方法具有较高的预测精度，从而也验证了方法的有效性与可行性。

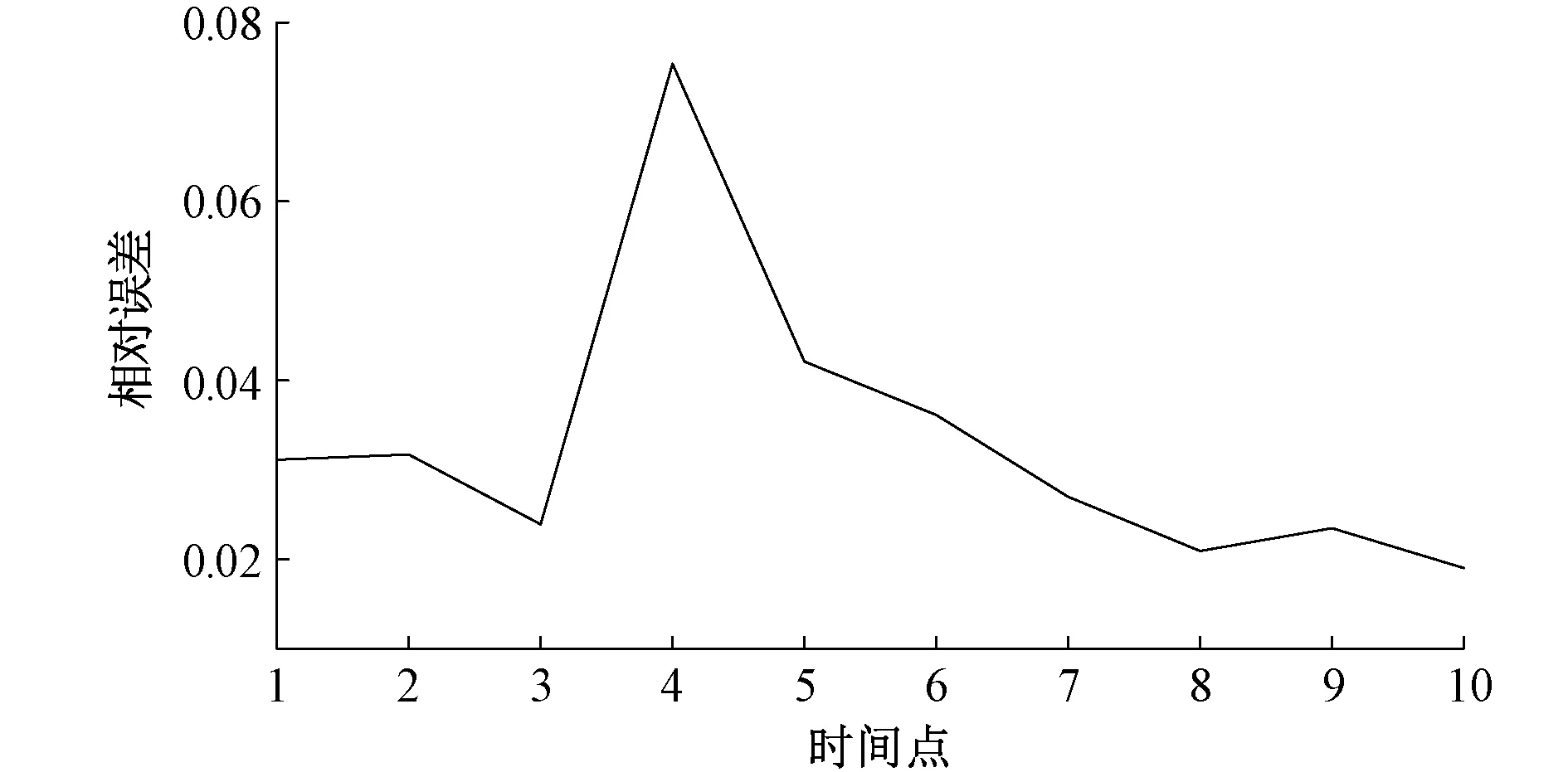
图8 预测相对误差图Fig.8 Predictive relative error rate

3 基于趋势变化分段的电力负荷组合预测方法

根据前面的分析可知，基于趋势变化分段的电力负荷预测方法在每个时段分别采用单一不同的预测方法，可有效提高电力负荷预测精度。为进一步提高预测精度，考虑在每个时段分别采用多种预测方法加权组合方式，这种方法称为基于趋势变化分段的电力负荷组合预测方法。早低谷时段，线性回归法、趋势变化预测法和BP神经网络预测法预测误差相对较低，故该时段采用上述三种方法加权组合，同理可得到其他五个时段的组合方式，如表5所示。

表5 六个时段对应的组合方式

根据表5，采用加权组合方式可得基于趋势变化分段的电力负荷组合预测方法的数学模型，其中P1表示早低谷时段预测模型，a11和a12表示早低谷预测模型加权系数；P2表示早高峰时段预测模型，a21和a22表示早高峰预测模型加权系数；P3表示午低谷时段预测模型，a31和a32表示午低谷预测模型加权系数；P4表示午高峰时段预测模型，a41和a42表示午高峰预测模型加权系数；P5表示晚低谷时段预测模型，a51和a52表示晚低谷预测模型加权系数；P6表示晚高峰时段预测模型，a61和a62表示晚高峰预测模型加权系数；PMR表示线性回归法预测结果，PMT表示趋势变化预测法预测结果，PMB表示BP神经网络预测法预测结果，PMS表示支持向量机预测法预测结果。

(5)

基于趋势变化分段的电力负荷组合预测方法的数学模型建立后，预测电力负荷前，需要求解模型参数。本文基于最小二乘法的思想，利用该地区40个工作日的历史负荷数据训练数学模型，从而得到最优参数，求解步骤如下，以早低谷时段为例进行说明：

步骤1：确定基于趋势变化分段的电力负荷组合预测方法的数学模型的参数取值范围和计算步长。基于加权组合原理，所有参数的取值范围为[0,1]；考虑到计算步长过小时，计算时间较长，而计算步长过大时，预测精度较低，因此文中将计算步长设置为0.01。

步骤2：根据参数取值变化，计算各时段预测结果。早低谷时段预测模型加权系数a11和a12取值范围均为[0∶0.01∶1]，即a11和a12各要101种取值结果，则a11和a12共有10 201种组合方式，将a11和a12代入式(2)，则早低谷时段预测模型P1有10 201种结果。

步骤3：计算各时段对应的电力负荷实际值减去预测值的差值。将步骤2中得到的10 201种早低谷时段预测结果P1与该时段实际电力负荷作差，求取误差。

步骤4：求取最优参数。求解步骤3中误差最小值，该值对应的模型加权系数a11和a12，即为模型最优参数。

根据上述步骤，求解得到了基于趋势变化分段的电力负荷组合预测方法的数学模型的最优参数，如表6所示。

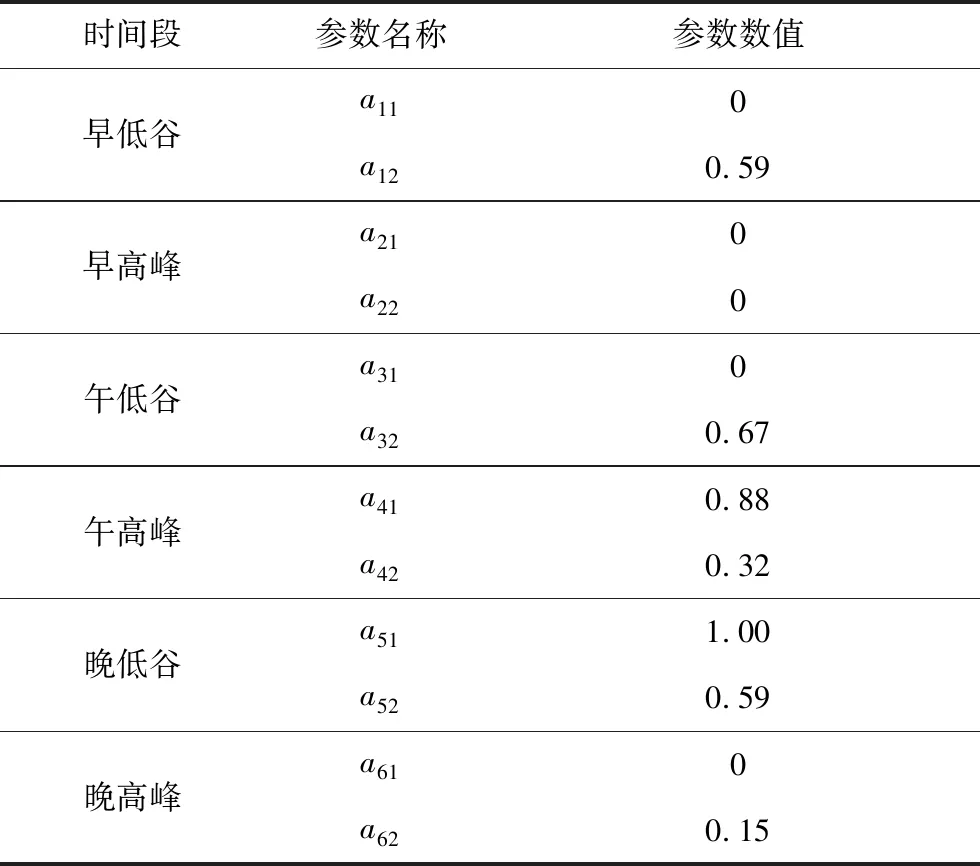
表6 模型最优参数

将表6中模型最优参数代入式(5)，即可实现电力负荷的预测，其各时段预测精度如表7所示，整体预测效果如图9所示，显然相对于基于趋势变化分段的电力负荷预测方法，基于趋势变化分段的电力负荷组合预测方法各时段预测精度都有所提高，整体预测精度达到了2.83%。

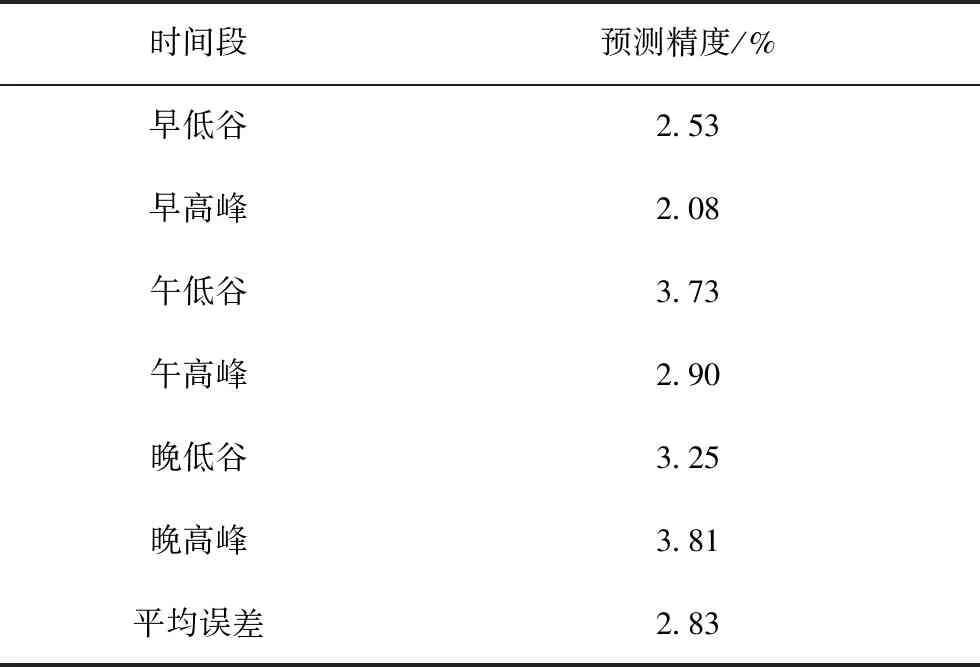
表7 各时段的预测精度

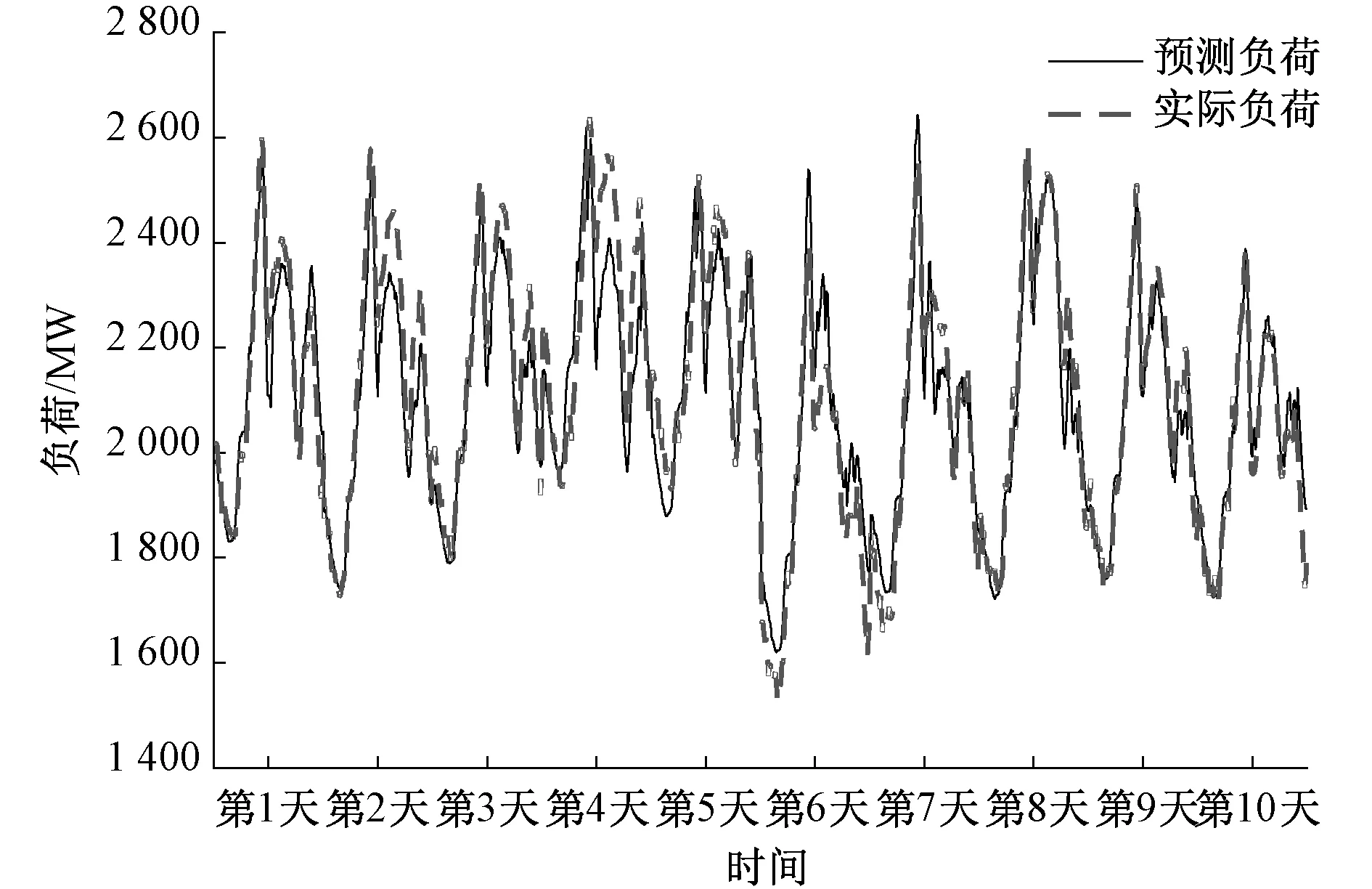
图9 整体预测效果Fig.9 Overall prediction

为了进一步分析预测效果，又绘制了10个工作日的相对误差图，如图10所示，显然采用基于趋势变化分段的电力负荷组合预测方法后，最大相对误差为4.70%，最小相对误差为1.80%，相对误差小于等于3%的天数为7个，占比70%，相对误差小于等于5%的天数为10个，占比100%，可见该方法可大幅度提高电力负荷预测精度，在电力系统中具有广阔的应用前景。

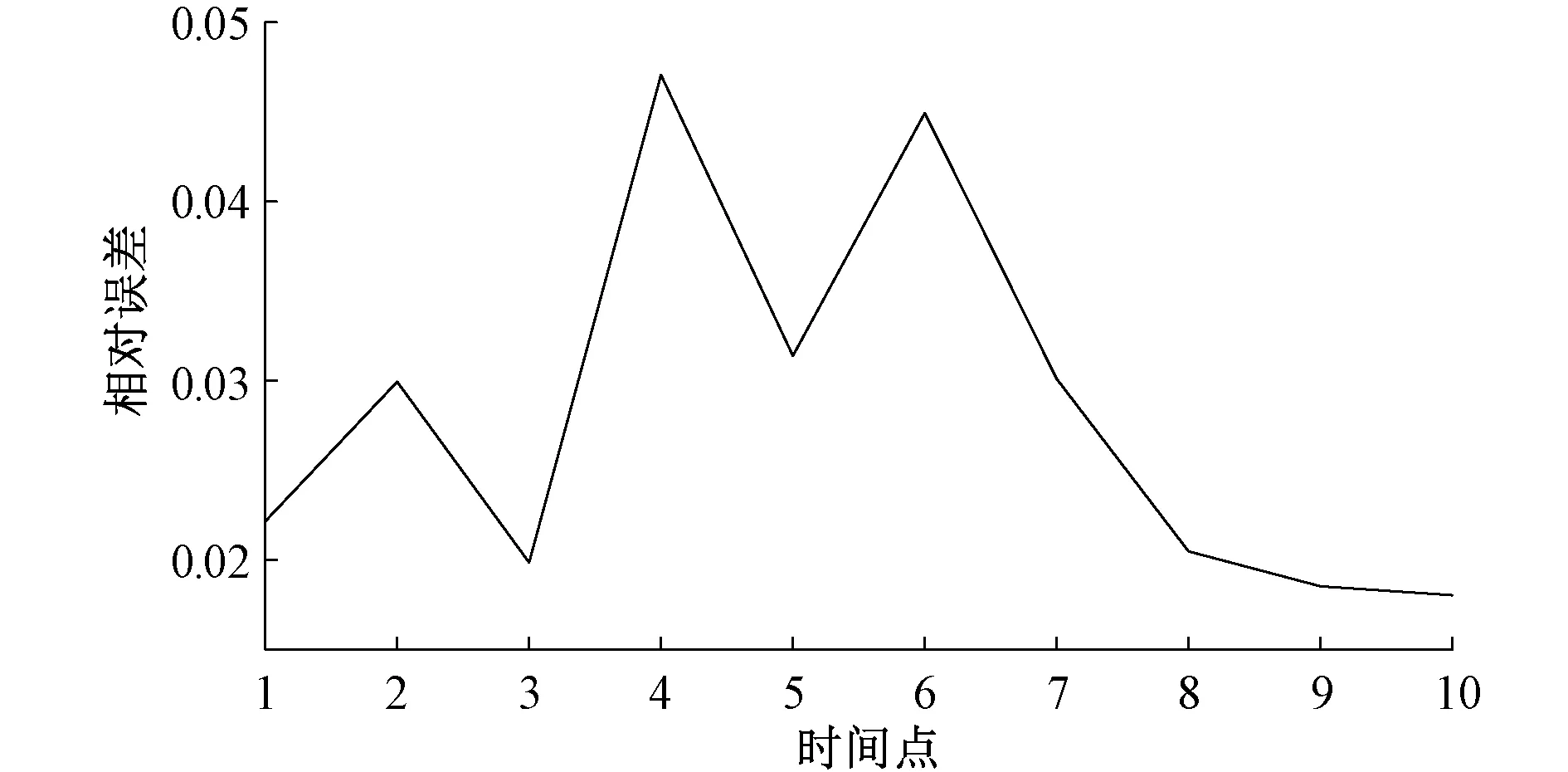
图10 预测相对误差Fig.10 Predictive relative error rate

4 结 论

(1)本文以苏北某地区电力负荷数据作为研究对象，分析了电力负荷的“三峰三谷”变化趋势，并基于连续性原理，将电力负荷变化曲线划分为六个时段。

(2)在充分研究线性回归法、趋势变化法、BP神经网络和支持向量机四种电力负荷预测方法的基础上，基于电力负荷“三峰三谷”变化特性，提出了基于趋势变化分段的电力负荷预测方法。

(3)基于加权组合思想，提出了基于趋势变化分段的电力负荷组合预测方法，同时借助最小二乘法求解得到了模型最优参数，最后通过算例验证了方法的有效性与可行性。