非均匀应力场影响下的裂缝扩展模拟及投球暂堵优化
周 彤 陈 铭 张士诚 李远照 李凤霞 张 驰
1.中国石化石油勘探开发研究院 2.中国石油大学(北京) 3.中石化重庆涪陵页岩气勘探开发有限公司
0 引言
水平井分段多簇压裂是实现致密油气储层高效开发的关键技术之一[1]。现场井下射孔成像、分布式光纤温度和声监测结果表明,压裂过程中各簇裂缝存在着明显的非均匀进液与扩展现象[2-3]。相关研究成果也表明,储层的非均质性和多裂缝扩展产生的应力干扰等因素,是造成水力裂缝非均匀扩展的主要原因[4-7]。因此,如何使压裂段内各簇裂缝均衡扩展,提高水平井段水力裂缝的覆盖率,是一个值得关注的现实问题。
近年来,一些学者着手研究促使多裂缝均衡扩展的控制方法,主要将储层应力分布视为均匀状态,提出采用非均匀的射孔簇或射孔参数来减少诱导应力的干扰,从而促进多裂缝均衡延伸[8-12]。但是,压裂前由于受到储层非均质性认识程度不足与现场施工工序等因素的影响,射孔优化方案在实施过程中存在着一定的难度[10]。相比之下,投球暂堵工艺由于具有施工简单、成本低、储层伤害程度小等优势,目前在水平井分段多簇压裂中被广泛应用。暂堵球通过对优势扩展簇的孔眼进行封堵,促使各簇裂缝均衡扩展,实现了沿水平段储层的均匀改造。微地震监测结果也显示出投球后会产生更多的岩石破裂信号[13]。但是,目前针对压裂施工中实施不同投球暂堵工艺措施后多簇裂缝扩展形态的研究成果较少,致使现场投球暂堵工艺措施的制订缺少相关的理论支撑,影响了该工艺在压裂施工现场的应用效果。为此,笔者基于边界元方法建立了水平井“井筒—孔眼—裂缝扩展”全耦合模型,提出暂堵球分配的计算方法,进而模拟研究在初始非均匀应力场条件下进行段内暂堵转向时暂堵球的投球数量、投球时机、投球次数及其对多簇裂缝扩展的影响,以期为压裂优化设计提供理论支撑。
1 模拟方法
1.1 假设条件
忽略缝内流体向基质的滤失,假设水平井各段压裂时每簇射孔仅产生一条水力裂缝,裂缝扩展满足线弹性断裂准则。由于国内非常规油气储层水平地应力差均较大,多簇裂缝在扩展过程中发生偏转的现象受到抑制[10],因此,可以将压裂缝假设为平直裂缝。各簇裂缝的延伸受到缝间应力干扰、射孔参数和地应力等因素的综合影响,各簇裂缝中压裂液分流量发生动态变化。同时,由于井筒摩阻系数相对于射孔孔眼及缝内摩阻系数较小,可以忽略井筒沿程阻力损失的影响[9-11]。由于压裂现场所用暂堵球直径均大于射孔孔眼直径,假设一个暂堵球可以完全封堵一个孔眼[14-16]。在注入压裂液时投入暂堵球,根据暂堵球数量与流量分配来重新确定各簇射孔数量,从而来模拟暂堵球的封堵效果,如图1所示。
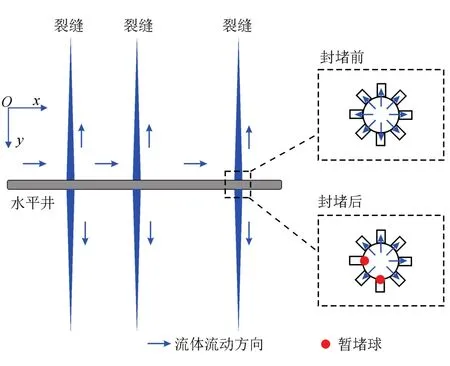
图1 水平井全耦合模型示意图
1.2 模型建立
1.2.1 固体弹性方程
裂缝宽度与净压力的关系可以通过边界积分方程来描述[17],即
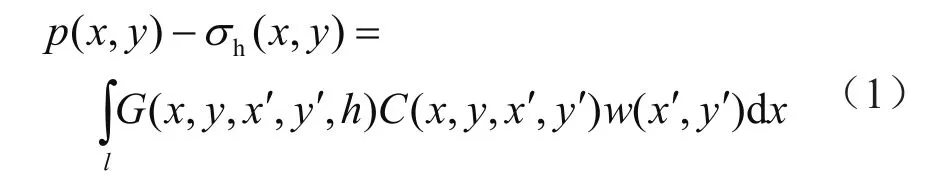
式中p表示缝内流体压力,MPa;x、y表示地层中任意点的坐标,m;σh表示最小水平主应力,MPa;l表示裂缝长度,m;G表示高度校正因子,无因次;x'、y'表示裂缝边界上任意点坐标,m;h表示裂缝高度,m;C表示格林函数,MPa/m2;w表示缝宽,m。
采用位移不连续法求解式(1),沿缝长方向将裂缝离散为一系列等长度单元,单元长度为∆x,单元半长为a,单元总数为M,任意一单元m坐标为(xm,ym)。裂缝上任意一点i的压力为所有裂缝单元在该处的诱导应力积分。式(1)的离散形式为[17]:
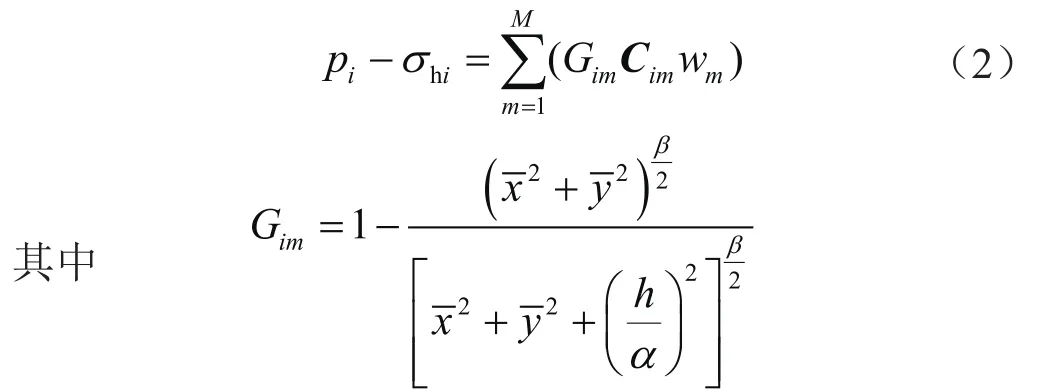
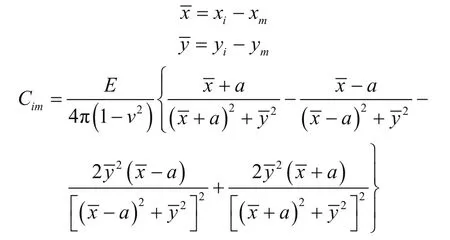
1.2.2 流动方程
流体在裂缝内的流动为层流[18],则满足下式:

式中q表示体积流量,m2/s;μ表示动力黏度,mPa·s。
考虑流体为不可压缩,则连续性方程为:
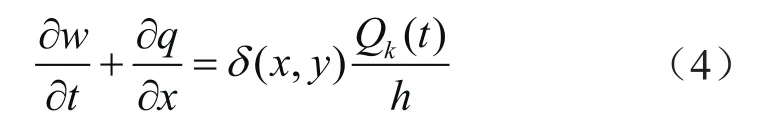
式中δ表示狄拉克函数,m-1;Q表示裂缝入口流量,m3/s;下标k表示裂缝编号,取值为1,2,…,N;t表示注入时间,s。
联立(3)、(4),得
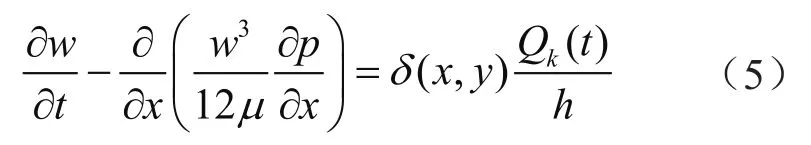
式(5)采用有限体积法求解[19],即
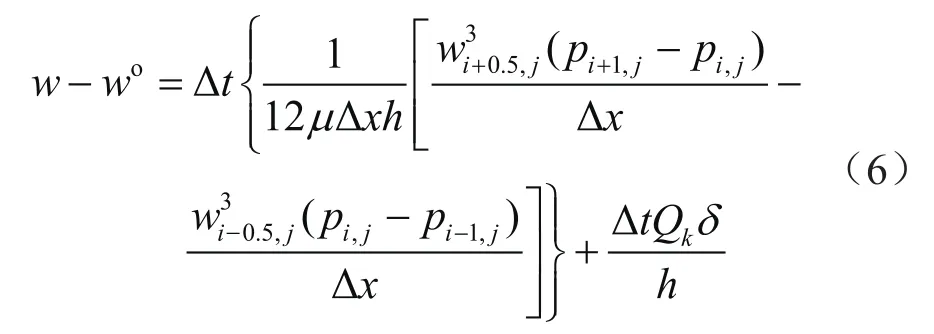
式中上标o表示上一时间步的裂缝宽度,m。
1.2.3 流量分配
压裂液经过井筒、孔眼进入裂缝系统,因此需要将流体在井筒—孔眼—裂缝中的流动进行耦合。总流量(Qto)的计算式为:

根据井筒内流体流动方程[20-22],不考虑流动摩擦阻力时,各簇裂缝对应的井底压力相同,有
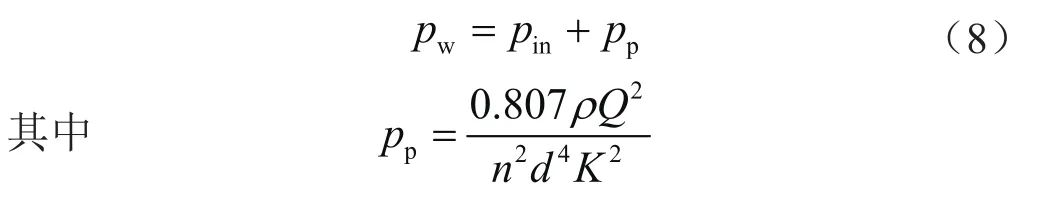
式中pw表示井底压力,MPa;pin表示裂缝入口压力,MPa;pp表示裂缝射孔孔眼节流阻力,MPa;ρ表示液体密度,kg/m3;n表示单簇裂缝射孔数,个;d表示射孔孔眼直径,m;K表示孔眼磨蚀修正系数,无因次。
1.2.4 暂堵球分配判断
注入暂堵球后,暂堵球由液体携带进入射孔簇,暂堵球数量的分配受各簇裂缝流量分配控制。采用向下取整分配暂堵球数量,每一簇实际分配暂堵球的余量计算式为:
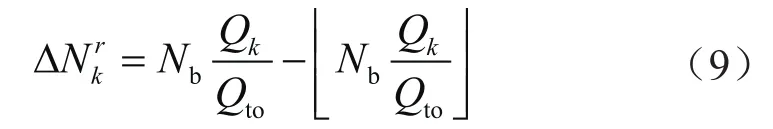
式中Nb表示注入暂堵球数量。
剩余暂堵球数量(Nl)计算式为:
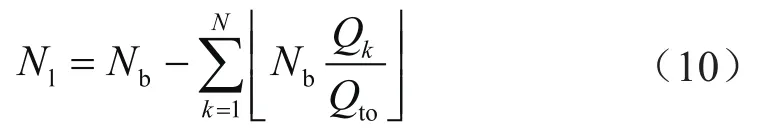
剩余暂堵球数量最多即为裂缝数量(N),按照余量从大到小来排序,将剩余暂堵球数量依次分配到对应裂缝。
1.2.5 边界条件与扩展准则
考虑裂缝尖端宽度和流量为零,即

式中下标tip表示裂缝尖端。
根据线弹性断裂准则,裂缝扩展时满足下式,即
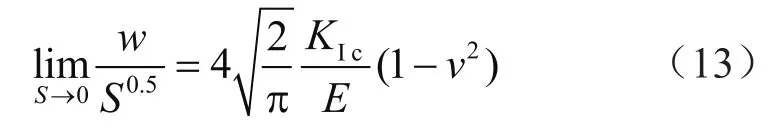
式中S表示距裂缝尖端的距离,m;KIc表示岩石I型断裂韧性,MPa·m0.5。
1.2.6 进液量差异评价
在模拟某时刻多簇裂缝的非均匀扩展程度时,可以利用裂缝进液量差异系数(Sd)来反映各簇裂缝进液量的差异,Sd越大表示各簇裂缝进液量差异越大,Sd计算式为:
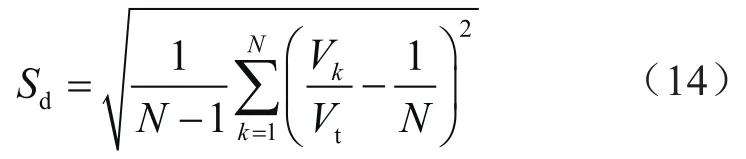
式中Vk表示进入裂缝k的液体体积,m3;Vt表示注入液体总体积,m3。
1.2.7 暂堵球分配计算方法
模型计算主要包括裂缝流固耦合方程的求解、井筒内流体的分配和裂缝扩展位置的确定。首先,根据上一步计算结果,假定裂缝入口流量,求解缝内流动方程,然后,根据缝内流动方程得到裂缝入口压力,进而得到新的裂缝中流量,至流量计算结果收敛为止;得到各簇裂缝流量后,根据尖端宽度判断裂缝是否满足扩展的条件,若满足则增加单元数量,否则,单元数量不变,递增时间步,进行下一时间步的计算,直到注入结束。其中,裂缝流固耦合方程、井筒流量计算方程均采用Newton-Raphson方法求解。若时间步达到暂堵剂加入的时刻,则进行暂堵球的分配计算,从而得到新的射孔数量,并用于井筒流量的分配计算。位移不连续系数矩阵利用上一时间步的影响系数矩阵来构建以节约系数矩阵的构建时间。
2 影响因素与相关分析
借鉴北美页岩油气的开发经验,密切割压裂+投球暂堵工艺试验已在涪陵、威荣等页岩气区块大力开展。为此,以单段6簇(HF1、HF2、HF3、HF4、HF5、HF6)密切割压裂为研究对象,压裂段长度为90 m,射孔簇区域居中设置,且簇间距为10 m,如图2所示。由于沿水平井筒的地应力分布对压裂段内各簇裂缝的起裂与扩展具有重要影响[9-11],为了研究非均匀应力条件下的多簇裂缝扩展行为,设置段内最小水平主应力沿水平井筒方向线性增加。在压裂过程中,通过加入不同数量的暂堵球来调整各簇裂缝中流量的分配,模拟参数如表1所示。
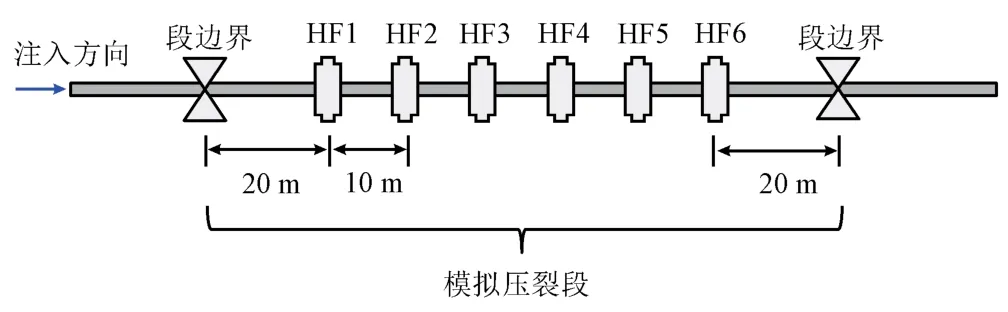
图2 模拟压裂段射孔簇平面分布示意图
2.1 平面应力非均匀性
2.1.1 不考虑投球
当初始最小水平主应力均匀分布(∆σh=0 MPa)时,各簇裂缝在扩展过程中由于受到诱导应力干扰的影响,中间簇裂缝长度低于外侧裂缝长度(图3-a),从而使中间簇裂缝的进液量略低于外侧裂缝。如图3、4所示,当初始最小水平主应力在平面上非均匀分布时,各簇裂缝扩展形态与裂缝进液量将发生变化;随着∆σh增加,各簇裂缝非均匀扩展程度逐渐增大;∆σh由0增至5 MPa时,Sd由1.23%增至11.85%;压裂段内位于高应力区域射孔簇的进液量明显减少,而位于低应力区域射孔簇的进液量明显增加;压裂段内∆σh为4 MPa、5 MPa时,高应力区域出现无裂缝起裂的射孔簇。
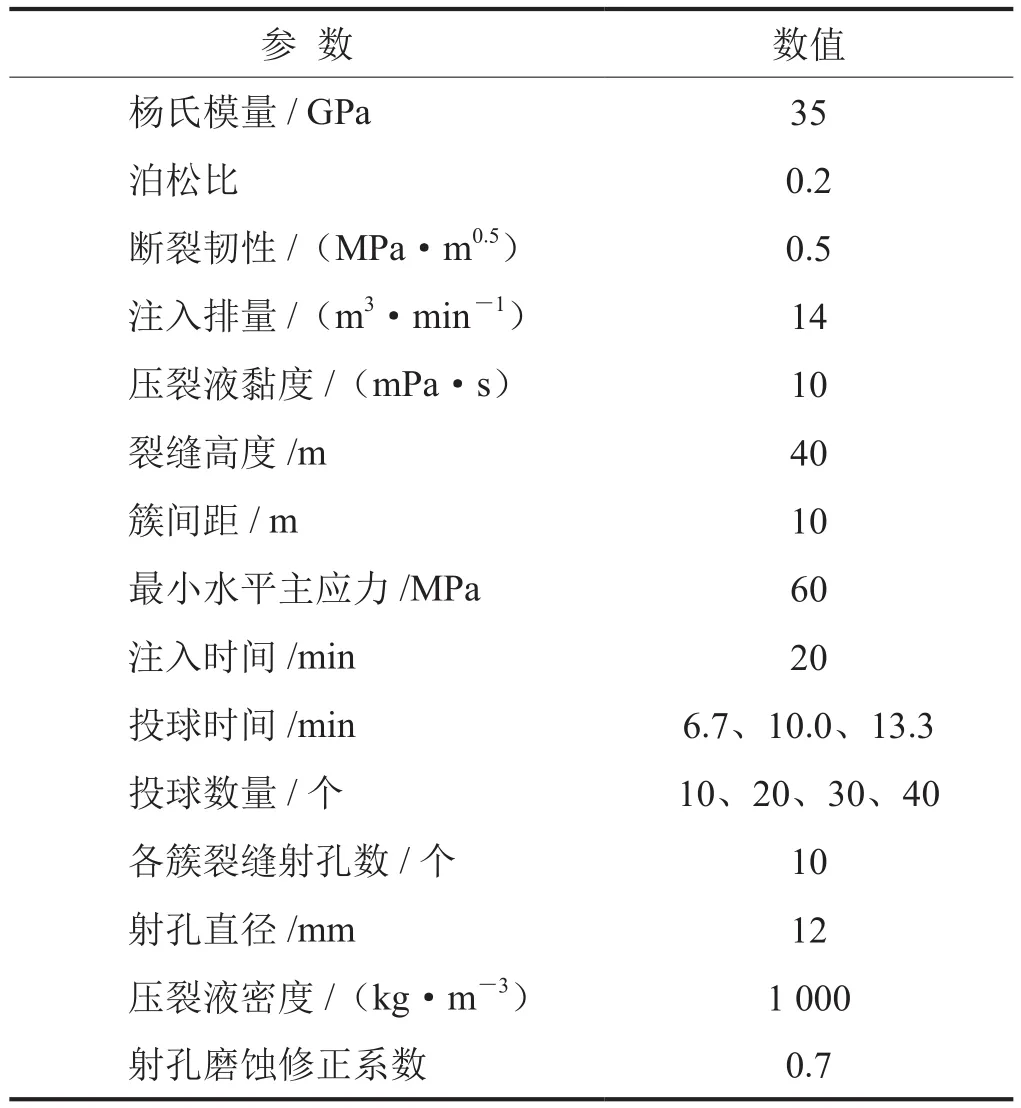
表1 模拟参数表
图5为不同∆σh条件下,各簇裂缝在延伸过程中射孔孔眼摩擦阻力(简称孔眼摩阻pf)在不同注入时间(t)的变化情况。在∆σh=0 MPa时,考虑孔眼摩阻后近井区域各簇裂缝扩展产生的诱导应力差最大为1 MPa,而各簇裂缝孔眼摩阻介于1.0~1.5 MPa。根据Lecampion等[11]的研究,当孔眼摩阻产生的压降与缝间诱导应力差相近时,各簇裂缝的扩展会相对均匀。射孔孔眼摩阻的限流作用平衡了诱导应力干扰带来的进液量差异,使得各簇裂缝中流体流动受到的阻力差距缩小,多簇裂缝相对均匀扩展。若不考虑孔眼摩阻的影响,各簇裂缝扩展形态会存在明显差异[10]。由美国Texas西部Midland盆地一口压裂井的侧钻取心结果,发现存在大量小间距(由数厘米到数米)平行水力裂缝[23],说明较小缝间距下多裂缝也可以同时延伸。因此,多裂缝竞争扩展产生的缝间诱导应力场并非是簇间裂缝产生非均匀扩展的主要原因。当考虑∆σh影响后,发现随着∆σh增加,多裂缝非均匀扩展程度增大。
2.1.2 考虑投球

图3 不同∆σh下裂缝扩展形态结果对比图
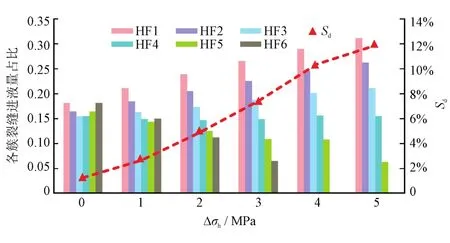
图4 不同∆σh下各簇裂缝进液量占比及对应Sd统计图
投球前,各簇裂缝的延伸受到缝间应力干扰、射孔参数和地应力等因素的综合影响,各簇射孔孔眼的进液量存在着差异。初始应力分布非均匀性越强,差异则越大。投球后,根据流量实时分配情况分配暂堵球,对优势进液射孔簇的孔眼进行封堵,使有效射孔数与进液量发生变化。如图6所示,当∆σh等于4 MPa时,通过使用暂堵球对优势进液簇HF1~3进行了封堵,孔眼封堵比例高于70%,封堵后进液量占比大幅度下降;以HF1簇为例,封堵后进液量占比由29.3%将至8.9%,而投球前基本无进液的HF6簇,在投球后进液量占比增至26.5%,且HF6簇的缝长与缝宽也迅速增加。图7为相同模拟参数下投入暂堵球与不投暂堵球的裂缝模拟结果对比,明显看出投球后位于高应力区的压裂簇裂缝得到有效延伸,模拟结束时的各簇裂缝扩展程度也更为均匀。
2.2 投球数量
在平面应力非均匀分布的影响下,在总注入时间的中间时刻进行投球,如图8所示,投球暂堵后由于射孔孔眼摩阻增大,井底压力(pw)明显增高;随着井底压力升高,投球后井底压力曲线呈现出二次破裂迹象(∆σh=4 MPa、5 MPa),表明在投球暂堵前没有发生裂缝起裂或裂缝扩展严重受限的无效射孔簇产生了新裂缝;同时,投球封堵射孔数量越大,产生的射孔孔眼摩阻越大,暂堵后的施工压力则越高。因此,对于埋深大、施工压力高的储层,过度的暂堵球用量会导致孔眼摩阻过高,大幅度增加井口压力,限制了排量的提升,对形成复杂裂缝以及增大改造体积不利[24]。
如图9所示。当段内∆σh=1 MPa、投球数量(Nb)为20个时,Sd仅为0.90%,裂缝进液量分配均匀;随着段内∆σh增加,Sd越大,可以通过增加Nb来获得较低的Sd;∆σh=5 MPa、Nb=40个时,Sd为3.04%。因此,当平面应力差异较小时,可以减少投球数量,若平面应力差异较大,可以适度增加投球数量来获得较均匀的裂缝进液量。
2.3 投球时机
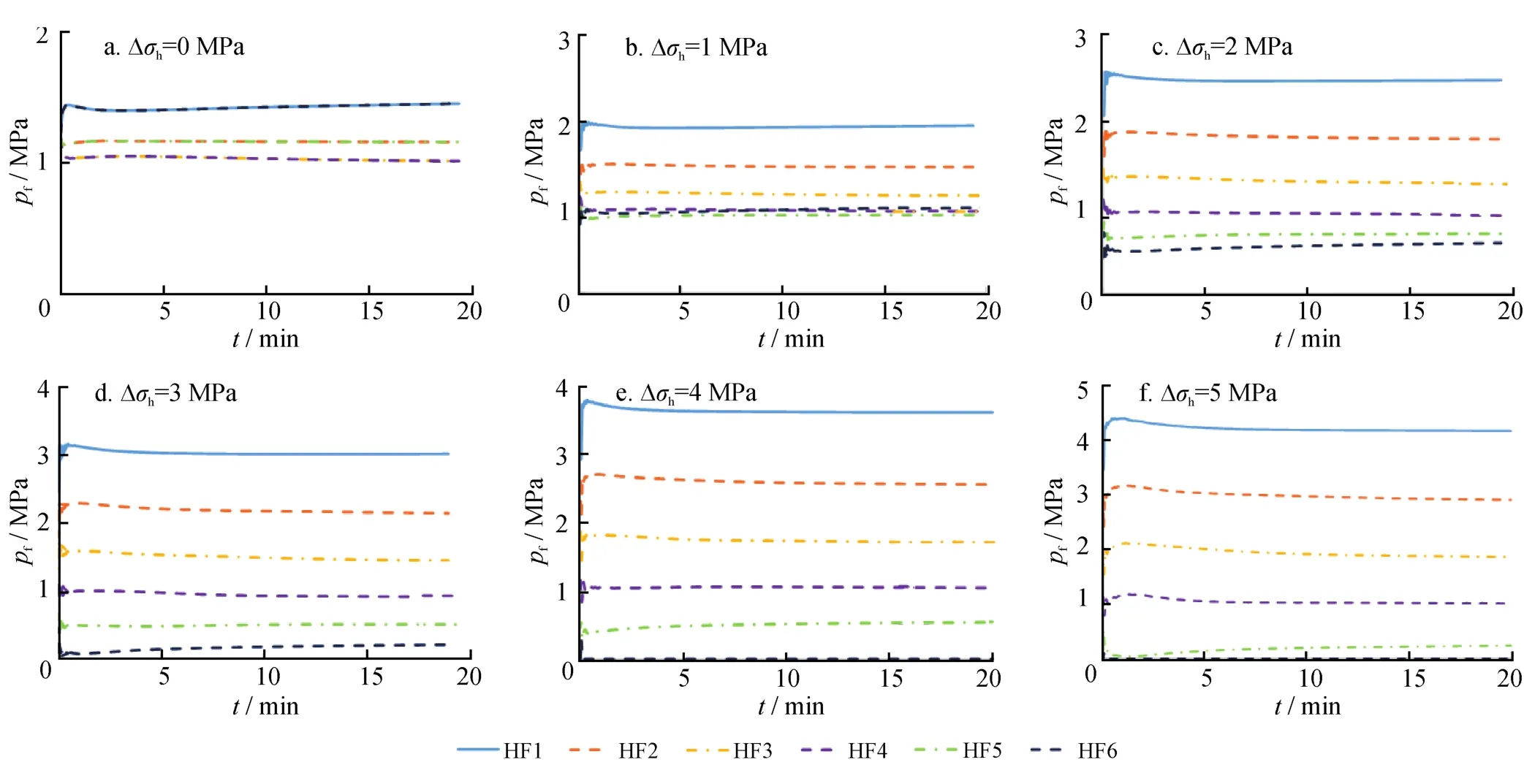
图5 不同∆σh下各簇裂缝pf—t关系曲线图

图6 投球对有效进液射孔数、进液量占比及裂缝长度与宽度影响结果图(∆σh=4 MPa)

图7 投球与不投球情况下裂缝扩展形态结果对比图(∆σh=4 MPa)

图8 投球数量对井底压力影响曲线图
如图10所示,若段内∆σh低于2 MPa,投球数量越多、投球越早,各簇裂缝进液量差异越大;应力差异较低时,投球时机处于总注入时间的中后期,裂缝进液量差异较小;随着段内∆σh增加,裂缝进液量差异受到投球数量(Nb)和投球时机的综合影响。在高∆σh条件下,若Nb小于20个,在早期投球裂缝进液量差异较小;随着投入暂堵球数量增多,最佳投球时机会发生改变。在Nb为30个、∆σh=5 MPa的条件下,时进行投球暂堵,Sd最低,为2.7%;Nb为40个时,在中期偏后时进行投球暂堵反而效果较好。因此,当平面应力差异较小时,可以适当减少投球数量、延后投球时间;当平面应力差异较大时,需要提前投球,尽早封堵优势进液孔眼,从而减小裂缝进液量差异,但同时也需要充分考虑孔眼过度封堵的问题。
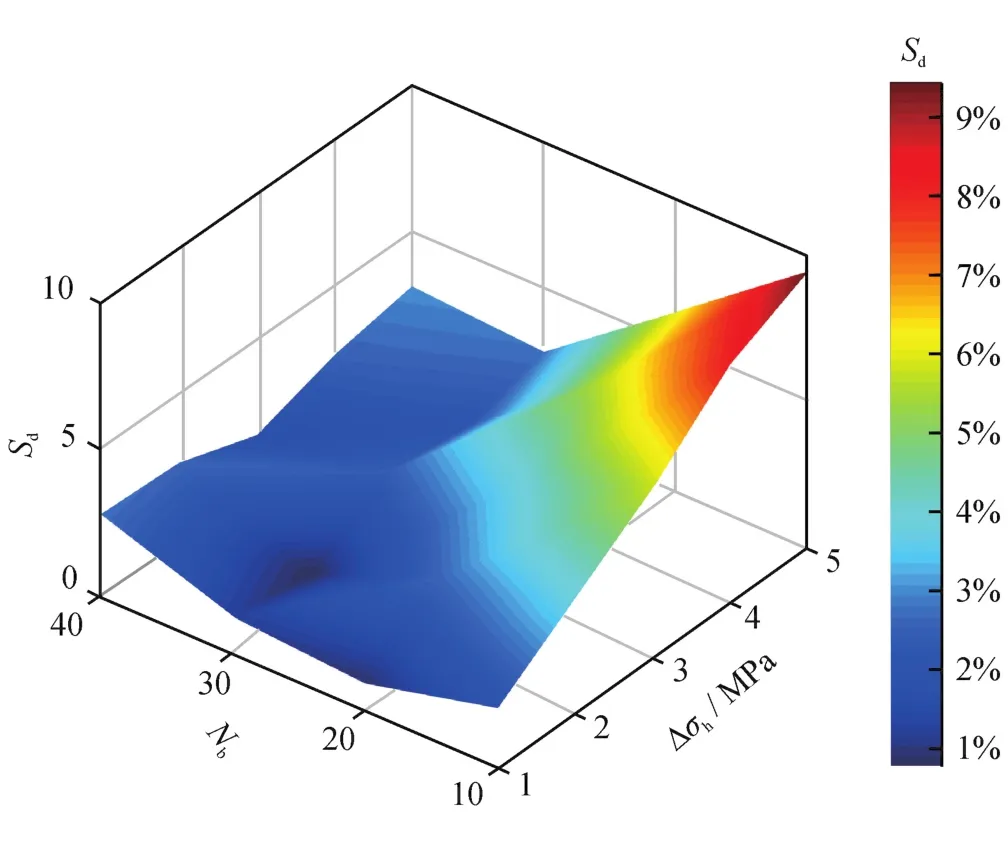
图9 Nb、∆σh对 Sd影响结果图
2.4 投球次数
除了考虑投球数量、投球时机对各簇裂缝扩展的影响外,分批投球也是现场施工常用的一种技术手段。模拟计算时,根据投球次数将暂堵球数量进行平分,得到每次投球数量。以两次投球为例,每次投球的时机分别处于总注入时间的1/3和2/3处。如图11所示,在∆σh介于4~5 MPa时,二次投球对应的Sd整体低于一次投球,这主要是因为二次投球时,一定比例的暂堵球将优势进液孔眼提前进行了封堵;而∆σh较低时,由于二次投球存在过早封堵的问题,Sd整体高于一次投球。
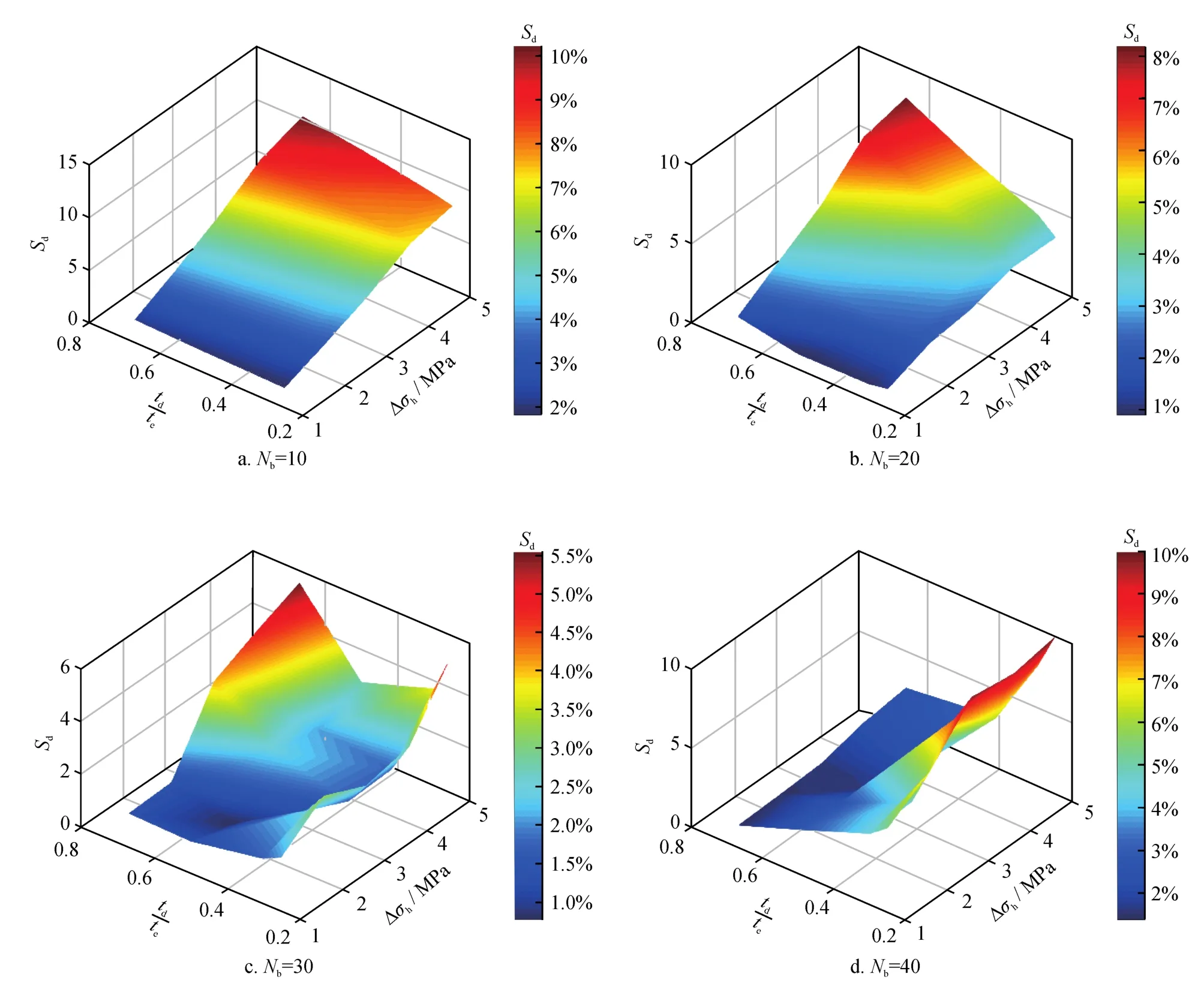
图10 不同Nb下对Sd影响结果图
3 结论
1)压裂过程中,射孔孔眼摩阻的限流作用会平衡诱导应力干扰带来的进液量差异,使得各簇裂缝中流体流动受到的阻力差距缩小。
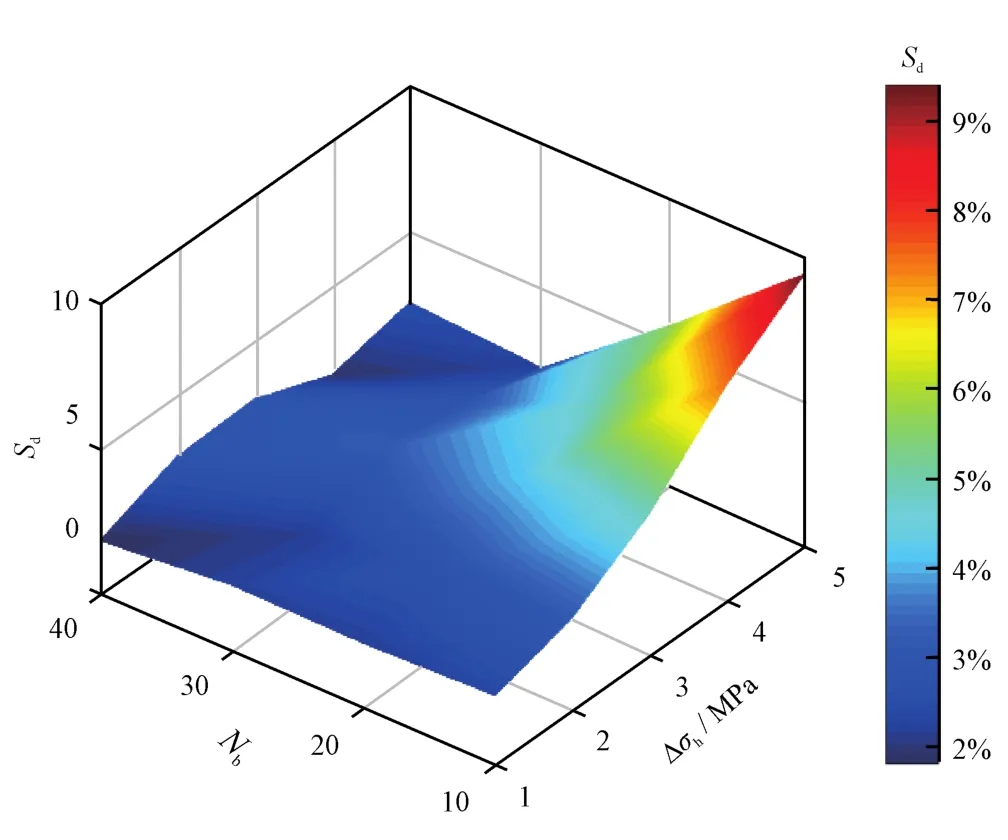
图11 两次投球情况下Nb、∆σh对Sd影响结果图
2)当考虑初始应力场非均匀分布的影响后,各簇裂缝进液量发生明显变化,高应力区域甚至出现不进液的无效射孔簇,而实施投球后,无效射孔簇会产生新裂缝。
3)当初始∆σh较大时(超过3 MPa),在施工中期适当增加投球数量(大于总射孔数的一半)或在中前期进行投球暂堵(包括在中前期分批次投球),有利于降低各簇裂缝的非均匀扩展程度。
4)当初始∆σh较小时(低于2 MPa),应减少投球数量或在施工中后期投球,否则会加剧各簇裂缝的非均匀扩展。
——基于博弈论视角

