拉床构件的有限元分析及拓扑优化设计

何玉辉，关健鹏，谢欣彤

中南大学机电工程学院，湖南 长沙 410083

当前制造业面临着产业升级和转型，在这个背景下相关企业对所生产的产品要求更合理的结构与更优良的性能。有限元分析是随着当前计算机性能的不断发展而得到愈加广泛和深入应用的一种工程问题研究方法，为工程师设计新产品和改进已有设计提供了新的分析途径，能够降低生产成本，缩短设计周期。结构拓扑优化通过改变结构原有的拓扑构型，使得结构上的所有材料都发挥作用，避免冗余结构的出现[1]。结合有限元分析技术、拓扑优化理论和传统力学分析的结构优化流程在结构设计领域被用户广泛采用[2-4]。

段明德[5]等以机床床鞍为研究对象，约束静态刚度和固有频率，对床鞍进行轻量化设计。戴护民[6]通过对成型机轴承座进行拓扑优化，使轴承座的动态响应特性得到改善，Y、Z 两个方向的一阶固有频率和动刚度都有所提高。尹辉俊[7]等利用变密度法的拓扑优化技术对乘用车的副车架进行了正向重新设计，有限元分析结果显示各种工况下的应力水平都低于原设计。传统的结构设计过程中通常很难确定改进后结构的动态特性，上述的研究工作通过有限元分析和拓扑优化过程避免了这个问题，并在此基础上进行了轻量化设计和结构优化，但在研究过程中缺少实验验证，无法确定所建立的有限元模型是否准确描述了结构的实际工况。

此外，拉床的墙板作为拉削加工过程中直接与夹具接触的部件，其动静态特性对拉床加工过程中的稳定性和工件加工后的质量具有决定性的影响，但现在少有对墙板结构性能分析和优化的研究。

本文在通过有限元仿真软件，对拉床墙板进行静力和模态分析，并通过对墙板模态试验检验有限元分析的准确性，之后利用拓扑优化的方法对墙板结构进行优化设计，以改善其动静态特性。

1 拉床墙板的有限元仿真分析

1.1 拉床结构分析

拉床由于有着极高的生产效率和加工精度，在现代制造业的大批量生产中得到广泛的应用，尤其适用于汽车、航空航天以及燃气轮机等行业中具有复杂几何形状的槽和内孔的加工，为企业降低加工成本发挥巨大作用。本文研究对象为型号YYLC6110 卧式内拉床的墙板，该拉床的主体结构如图1 所示。机床允许的最大拉力为100 kN，最大行程为1100 mm。

墙板为加工过程中的主要受力位置，其上要安装夹具及工件，内侧由导柱支承，导柱末端有螺纹，通过螺母将墙板压在导柱上，墙板下部由螺栓固定在机架上。墙板的静、动态特性将直接影响机床的加工质量。

图2 有限元前处理结果Fig.2 Results from Finite element preprocessing

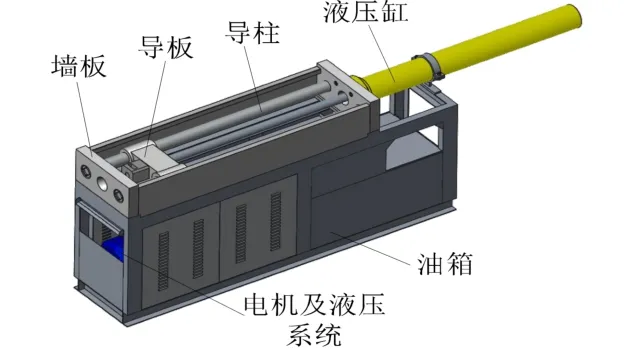
图1 卧式内拉床主体结构Fig.1 The main structure of horizontal internal broacher

1.2 有限元前处理

墙板主要外形尺寸为425 mm×200 mm×55 mm，材料为Q235。墙板正中位置为拉削孔，拉削孔两侧的沉孔为导柱安装孔。因其结构比较简单，直接在hypermesh 软件中建立墙板的几何特征，忽略对结构强度影响不大的细孔等其它特征，并进行网格划分。为提高计算效率和计算精度，采用六面体单元对实体进行离散化，共生成43572 个节点和37267 个六面体单元，结果如图2 所示。三个孔处的圆环是为了方便后续进行结构优化，将优化区域和非优化区域进行了分离。

1.3 有限元静力分析和模态分析

在有限元软件中建立两个工况来分别进行静力分析和模态分析，以获取墙板在载荷作用下的应力应变情况以及动态特性。两个工况的约束均为固定两个沉孔的中心以及墙板下部螺栓位置，进行静态分析时，在拉削孔的中心施加一个大小为100 kN 的集中力，方向沿-Z 方向，然后在OptiStruct模块中进行求解。

静力分析结果如图3 所示，从应力应变的分析结果中可以看到，最大应力位置在墙板内侧导柱安装孔的靠近中心处，最大应力为182.9 MPa。墙板材料的屈服强度为235 MPa，可知当承受许用的最大载荷时，安全系数仅为1.28 左右，因此可以在优化设计时降低最大应力，从而提高安全系数。墙板变形的最大应变位置在墙板外侧拉削孔的圆周上，最大变形量为0.032 mm。

图3 墙板有限元静力分析结果Fig.3 Finite element analytical results on wallboard

模态分析结果的前四阶固有频率及振型如图4 所示。一阶模态为上下部绕X 轴的前后扭转，二阶模态为四角处绕Y 轴扭转，三阶模态为左右部的前后摆动，四阶模态为中部的前后摆动。拉削过程中的激励频率为f=(v×1000)/(p×60)，v为额定拉削速度3 m/min，p为拉刀刀齿间的距离，拉床配套的宽刀体键槽拉刀齿距为8 mm，由此可得激励频率为6.25 Hz，与墙板的一阶固有频率538 Hz 相距较远，难以引起共振，因此墙板的动态特性符合使用要求。

图4 墙板前四阶模态分析结果Fig.4 Analytical results of wallboard in the first four modes

2 墙板模态的试验测量与分析

2.1 模态测量方案

模态测量时，使用力锤敲击墙板结构产生激励，然后通过加速度传感器将各测点的加速度信号转化为电信号，并由数据采集前端完成数据的收集，最后前端将数据传输到上位机，进行数据的分析处理。试验所采用的试验设备如表1 所示，试验现场的图片如图5 所示。

表1 模态测量试验设备Table 1 Equipment measuring modes in test

在布置加速度传感器的测点时，首先要求不能将所有传感器放置在所关心模态的节点位置，否则将无法获得模态振型。其次需要有足够多的测点数量，以便区分和描述各阶模态的振型[8]。但是如果布置太多的测点又对设备的通道数目提出更高要求，同时也会加大测试的工作量，所以要合理地安排测点数量和布置测点位置。根据有限元模态分析的结果，对墙板模态测试的测点布置安排如图6 所示。在墙板的长度方向(X 方向)布置4 个测点，在高度方向(Y 方向)布置3 个测点，在厚度方向(Z 方向)布置2 个测点。与图4 中的前四阶模态的振型进行对比，可以看出这样的测点安排能够合理区分和描述各阶模态的振型。为减小干扰对结果的影响，每个测点进行8 次测量，取平均结果得到各个测点的频率响应函数。

图5 模态测量试验现场Fig.5 Testing scene measuring modal shapes

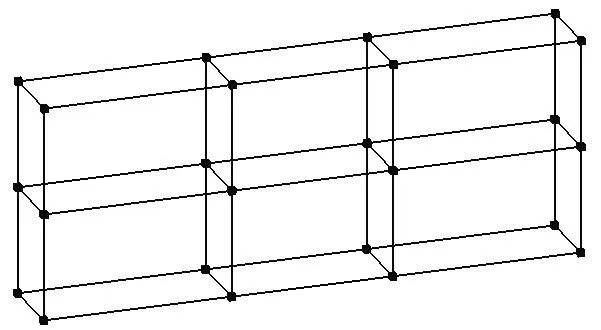
图6 测点布置安排Fig.6 Layout of testing points

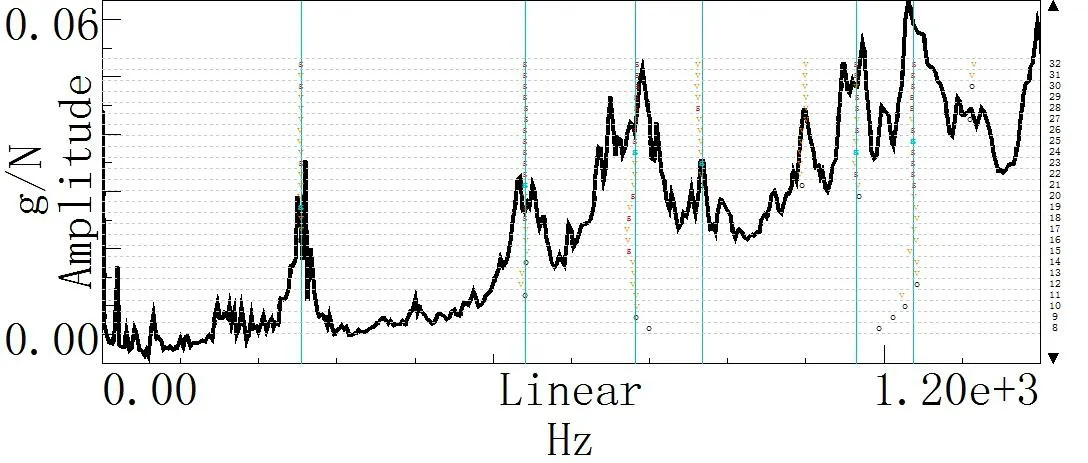
图7 模态分析结果曲线Fig.7 analytical curve of mode shape

2.2 模态测量结果与对比分析

利用Test.lab 的模态分析模块，在模态测试数据选择中选取所有测得的频率响应函数作为要分析的数据，设定分析带宽为0～1200 Hz，应用软件内置的PolyMAX 方法对带宽范围内的稳定模态进行识别，PolyMAX 方法能够对各阶稳定模态的频率和振型进行高精度的识别，并且有极高的计算效率[9]。稳定模态的分析结果如图7 所示。

表2 墙板模态试验结果与有限元结果的对比Table 2 Comparison of wallboard mode results and finite element results

Test.lab 软件会给出各个极点的稳定状态，其中s表示该处的频率、阻尼和向量的稳定情况都满足公差范围要求，据此可以选择各阶稳定模态，并计算各阶模态的振型。在设定的带宽范围内各阶稳定模态的频率、阻尼比以及与有限元分析结果的对比见表2，其中ζ表示阻尼比，fT 为各阶固有频率的试验结果，fFE 为各阶固有频率的有限元分析结果，ε为相对误差。试验模态的一阶固有频率为255 Hz，在有限元分析结果中难以找到与其相匹配的结果。这可能是由于墙板的试验模态是墙板装配于整机上的状态下进行测量的，因此可认为试验结果的一阶固有频率属于整机的其它部件，去除该频率后与有限元结果进行对比，误差在可接受范围内，说明了有限元分析过程的可靠性。去除第一阶结果的试验模态振型如图8 所示，从振型上来看，也基本与有限元结果相近。

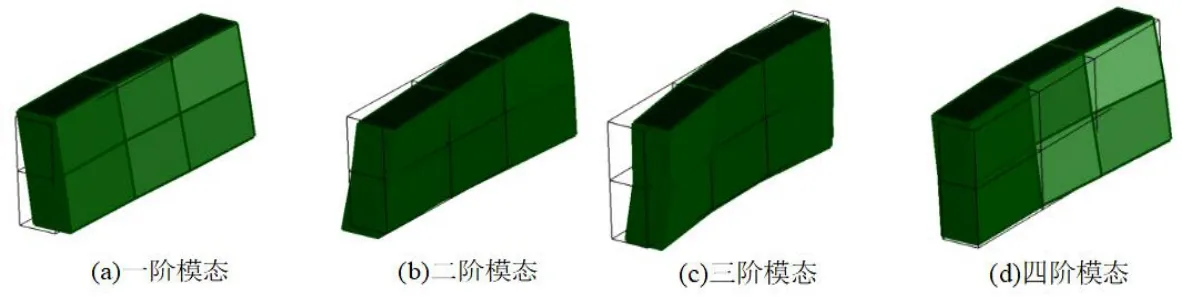
图8 试验模态的各阶振型Fig.8 Mode shape on each order

3 墙板结构的优化设计

3.1 拓扑优化理论基础

对结构进行拓扑优化的目的是为设计区域内的结构材料指定新的拓扑构型，从而达到最优设计目标，并且使结构在指定的边界约束和载荷响应等条件下，满足实际工况的需求[10]。在优化过程中为了避免出现难以求解的情况，要根据有限元模型建立一个显式近似模型，这样也可以减小计算的工作量。变密度法（SIMP）由于易于程序化实现且拥有较高的运算效率，被广泛选用为拓扑优化计算的数值模型[11]。本文在拓扑优化设计中使用的Optistruct 软件使用的就是变密度法中的插值模型。

3.2 墙板的拓扑优化设计

优化设计的目标函数设为最小化墙板结构上的最大单元应力，在优化过程中约束一阶固有频率大于初始值，同时要求优化后的体积不大于优化前的80%，以达到既改善墙板的静、动态特性又实现轻量化的设计目的。对墙板优化设计时，除了装配需要的安装位置，其它部分均定义为设计区域。

应用SIMP 法对墙板进行拓扑优化的数学模型可以描述为：

式中，xi为单元密度，即优化设计过程中的设计变量；strs表示单元应力；Vf为整体体积分数；K为墙板结构的刚度矩阵；U为节点位移矢量组成的矩阵；F为施加在墙板上的外载荷；fr1为一阶固有频率；xmin为最小单元密度，一般取其为0.001 以避免优化过程中出现奇异值。

将上述优化问题在Optistruct 中进行求解计算，优化结果在11 次迭代后收敛。在hyperview 中打开优化完成的结果，并约束可见的单元密度阈值为0.3，只显示需要保留的结构，其结果如图9 所示。

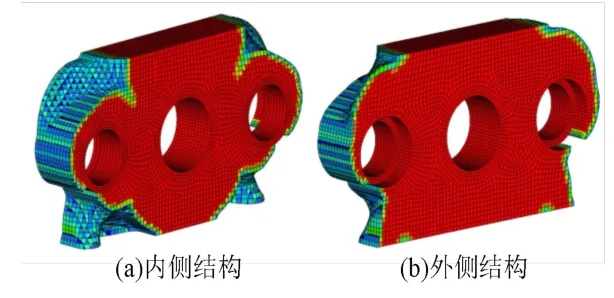
图9 墙板结构拓扑优化Fig.9 Topological optimization for wallboard structure

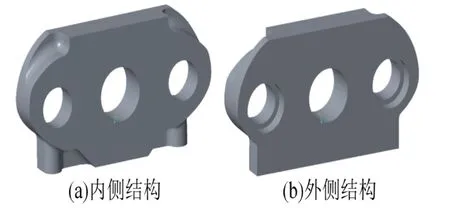
图10 墙板二次优化设计Fig.10 Second optimization design for wallboard

从图9 可以看出，墙板的中部位置作为主要变形区，大部分结构得以保留，两个导柱的安装孔周围也保留了较多的材料。墙板的四角处基本不承受载荷，在优化结果中此区域大多被去除。利用OSSmooth 模块将优化后的结果导出IGES 格式的文件，在三维建模软件CREO 中打开，以便根据优化的结果进行模型的修改和重新设计。二次设计后的墙板结构如图10 所示。

3.3 二次设计后的墙板性能分析与对比

将二次设计后的墙板结构导入到有限元软件中，在前处理完成后进行静力分析和模态分析，其中应力应变的分析结果如图11 所示。

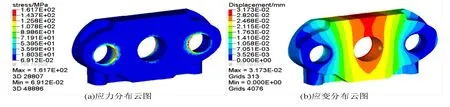
图11 二次设计后的应力应变分析结果Fig.11 Stress-strain analysis after second design

优化后与优化前的结构质量M，最大单元应力σmax，最大变形量Dmax以及一阶固有频率f1的对比数据可见表3。优化后墙板的质量减轻30.4%；最大应力减小为161.7 MPa，减小了11.6%，安全系数由1.28 提升到1.45；最大变形量改变不大，但也略有减小，减小了1.86%；一阶固有频率由原来的538 Hz 提升到了712 Hz，更难发生共振。经过对比可知，基于拓扑优化和有限元分析的墙板结构优化设计方法有效改善了其静、动态特性。

表3 优化前后墙板性能对比Table 3 Comparison of wallboard performances before and after optimization

4 结语

本文对拉床墙板进行有限元分析并对分析结果进行了验证，在此基础上对墙板结构进行了拓扑优化设计，以改善其静、动态特性。通过对优化后重新设计的结构进行分析对比，发现墙板质量减轻了30.4%，最大应力减小了11.6%，最大变形量减小了1.86%，一阶固有频率由538 Hz 提升到了712 Hz，实现了在轻量化的基础上提高结构刚度，改善动态特性的设计目标。

本文所使用的有限元分析和拓扑优化的设计方法，相较传统的设计方法更加清晰可靠，易于实现，并且通过实际测试验证了计算方法的准确性，为结构设计和改进提供了一种可借鉴的方法。