计算机动态测验中问题解决过程策略的分析：多水平混合IRT模型的拓展与应用*

李美娟 刘 玥 刘红云,4

(1北京教育科学研究院北京教育督导与教育评价研究中心, 北京 100036)

(2北京师范大学中国基础教育质量监测协同创新中心; 3北京师范大学心理学部;4北京师范大学心理学部应用实验心理北京市重点实验室, 北京 100875)

1 引言

问题解决能力是指在没有清晰解决方法的情境下, 通过一系列认知过程来理解和解决问题的能力(Mayer, 1982)。在这个过程中, 问题解决者必须充分理解问题的核心, 设计可行方案并实施, 且能够控制进度并达到目标(Garofalo & Lester, 1985)。问题解决能力对于学习和取得成功非常重要, 很多全球范围的大型教育测评项目都将其作为评价的重点。例如, 国际学生测评项目(Programme for International Student Assessment, PISA) (OECD, 2003,2013)等。近年来, 信息技术的进步和计算机测验领域的研究为问题解决能力提供了全新的测评方式。如2012年PISA采用计算机动态测验的方式, 通过模拟真实生活情境中的问题来考察学生的问题解决能力, 关注在没有明确解决方案的情况下学生运用一般认知过程的特征(OECD, 2013), 强调问题解决过程的动态变化和互动特征(Funke, 2001)。

计算机测验不仅可以改变测验设计、施测方式,甚至可以改变数据分析的方法(DiCerbo & Behrens,2012)。不仅可以考察学生是否正确作答, 而且可以通过系统自动记录基于时间的行为序列(Kerr,Chung, & Iseli, 2011), 记录学生解决问题过程中的时间以及学生完成任务的系列行为, 称为过程性数据(process data) (Zoanetti, 2010)。基于过程性数据不仅可以分析挖掘学生的解题过程策略, 同时也可以作为问题解决能力评价的证据(DiCerbo & Behrens,2012)。例如, Greiff, Wüstenberg和Avvisati (2015)基于PISA2012《室温控制》任务的过程性数据, 发现一次只改变一个操作变量的策略不仅能预测学生在该题上的表现, 也能预测问题解决总成绩。近年来, 随着测量理论和统计技术的发展, 问题解决过程及其技能和策略的探讨越来越被重视。其中一类是通过对该题目所需技能(或属性)进行标定, 基于一定的测量模型对解决问题过程的策略特点进行分析。最具代表性的方法是认知诊断模型的评估。如de la Torre和Douglas (2004)采用高阶潜在结构模型, 对学生能力进行估计, 并基于学生的认知属性掌握模式对其认知特征进行分类。另一类是借助统计模型和数据挖掘的思想, 对过程数据蕴含的丰富信息进行分析。常用的方法有可视化分析方法(DiCerbo, Liu, Rutstein, Choi, & Behrens, 2011)、聚类分析方法(Bergner, Shu, & von Davier, 2014)和分类分析方法(Desmarais & Baker, 2012)。最近, 也有学者(Shu, Bergner, Zhu, Hao, & von Davier, 2017)结合隐马尔科夫模型(Hidden Markov Model)和项目反应模型, 分析过程性数据中的序列作答信息,从而估计学生的能力。本研究探讨的方法属于第二类, 即基于过程数据分析学生在解决问题过程中的不同策略, 同时基于任务提交状态的信息进行能力估计。

过程性数据具有嵌套结构, 每个学生完成任务过程产生的行为序列(即, 过程水平的数据)嵌套于学生个体。因此, 可以借鉴多水平框架下的模型来分析过程性数据(Goldstein, 1987)。多水平混合项目反应理论模型(Multilevel Mixture Item Response Theory, MMixIRT)将多水平模型和混合项目反应理论模型相结合, 不仅可以提高模型参数估计的精确性, 同时可以获得不同潜在类别群体的测量特征(Cho & Cohen, 2010)。对于两水平的数据, MMixIRT可以在第一水平和第二水平进行非连续潜在变量(潜在类别)和连续潜在变量(能力)的分析, 第一水平的潜类别分析主要基于被试作答反应之间的关系, 第二水平的潜类别分析主要基于组内被试作答反应之间的关系(Vermunt, 2003)。虽然 MMixIRT为分析嵌套数据和类别特征提供了思路, 但是如果直接处理过程数据, 可能会带来两个问题：(1)过程中的一个步骤仅反映了被试在这一时间点的一次操作或行为表现, 不满足模型关于不同时间点的测量都是某一特质在这一时刻表现的假设。(2)采用问题解决的所有过程数据估计被试个体能力, 会带来问题解决不同阶段或不同步骤所测量特质的不统一而导致的估计值的偏差和解释上的困难。因此,传统的MMixIRT模型在模型假设和潜变量意义的解释上并不适用于过程性数据, 如何借助该模型的思想使其适用于处理过程数据是拓展模型拟解决的问题。

国际上已经有越来越多的研究关注过程性数据的挖掘, 分析不同群体学生解决问题的典型特征(Qiao & Jiao, 2018; Liao, He, & Jiao, 2019), 但是大多数研究只采用了学生作答的部分信息, 或者只关注类别而忽略了能力估计。很少有研究基于过程数据的嵌套特点, 同时关注问题解决策略类别, 以及个体层面信息所反映的问题解决能力水平。本研究以 PISA2012中一道问题解决题目为例, 基于5个国家(或地区, 以下简称地区)学生问题解决的过程性数据, 将 MMixIRT模型进行拓展, 并使用拓展后的MMixIRT模型分析学生在问题解决过程中的不同策略, 估计个体水平能力, 同时也对各地区使用策略的特点进行总结和比较。

2 拓展的MMixIRT模型

传统 MMixIRT模型的定义和详细介绍参见(Cho & Cohen, 2010)的研究。本研究对传统的MMixIRT模型做了两方面的修改和拓展。

首先, 为体现问题解决任务过程中行为序列连续性的特点, 将步骤的累计信息作为特定步骤的过程数据。可以表示为：

其中 ytki为第 k个学生 t时间点在 i得分点(类似于后面交通题目中的路径)上的操作行为。传统的 MMixIRT模型是直接对 ytki建模, 而拓展的MMixIRT模型是对累计反应 Yjki进行建模。如果时间t=j, wt=1, 否则 wt=0, 则变为传统的MMixIRT模型。结合测试题目和过程数据的特点, 采用累积反应作答作为过程j的反应作答, 即如果t≤j, 则wt=1。

其次, 为使得过程水平和个体水平变异的分解更加灵活, 定义设计矩阵A分解过程层面和个体层面的变异, 其中第j行 Aj用来定义过程数据不同层面潜变量的分解权重。拓展模型可以表示为：

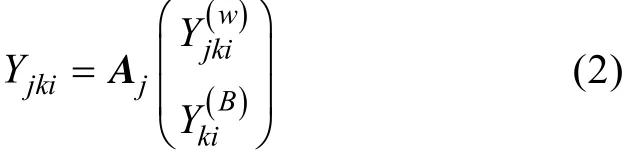
传统模型是拓展模型的特例。拓展模型和传统模型的区别主要表现在以下两个方面：(1)过程水平每一步骤的潜在类别是前面各个步骤的累积状态,而不是这一个步骤的表现, 描述累积状态不仅可以更好地解释解题过程策略的使用, 而且可以为探索策略使用的连续性和转换提供依据; (2)个体水平潜变量的定义所采用的测量指标与传统的 MMixIRT模型不同。传统模型中, 个体水平的潜变量是由第一水平的观测变量[yjk1, …, yjki, …, yjkI]估计得到(Lee, Cho, & Sterba, 2017), 而拓展模型中可以定义更加自由的设计矩阵 A决定个体层面能力估计所用到的信息。

3 本研究使用的拓展MMixIRT模型

拓展的 MMixIRT模型比较灵活, 可以在第一水平和第二水平模型中结合实际研究关注的重点定义不同的模型。结合过程数据的特点, 本研究主要关注学生在问题解决过程解题策略的差异和最终状态体现出个体能力的差异, 因此, 本研究使用的模型也是上述拓展模型的特例。

3.1 模型定义

本研究使用的拓展 MMixIRT模型包含两个水平：过程水平和个体水平。在过程水平, 定义潜类别来描述不同步骤的异质性, 从而对不同策略进行分类; 在个体水平, 定义连续潜变量来估计个体的能力。

过程水平模型：

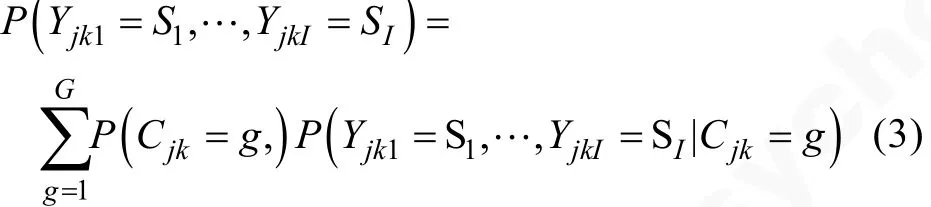
P（ Yjk1=S1,… ,YjkI=SI）表示第 k个学生(k=1,…,K)在第j个步骤(j=1, …,Jk, Jk表示学生k的步骤总数)后, 得分点上的作答状态为(S1,…,SI)的概率(需要注意的是, 每个学生完成任务所使用的步骤数 Jk是不同的); 其中 P （ Cjk= g）表示第 k个学生的第 j个步骤属于潜在类别 g的概率(g=1,2,…,G), G 为潜在类别数。 P ( Yjk1=S1,… ,YjkI=SI|Cjk= g)表示第 k个学生的第 j个步骤属于潜在类别g的条件下, 前面j个步骤的累积作答状态为(S1,…,SI)的条件概率。

个体水平模型：

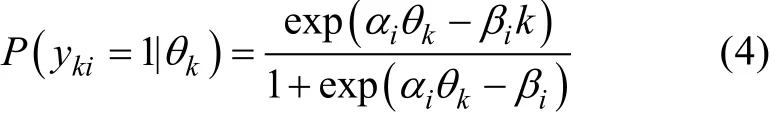
个体水平模型表示基于学生最终作答状态对个体水平的能力进行估计, 对应的设计矩阵A为：如果 j为被试最后一次提交状态的作答, 则Aj=（1,1）, 否则 Aj=（1,0 ）。在个体水平模型中, yki表示第k个学生在第i得分点上的作答。αi表示第i得分点的区分度参数, βi表示第i得分点的难度参数(i = 1,2,…,I), θk表示基于过程中最后一个步骤估计得到的学生k的能力估计值。假设θk服从标准正态分布(θk～N(0, 1))。

图1表示本研究使用的拓展MMixIRT模型的基本结构。图中的方框表示学生在过程中的作答反应, 圆形表示潜变量, 三角形中的 1表示元素均为1的常数向量(这一常数向量的系数对应截距参数βi,即传统IRT模型中的难度参数)。其中, 对于过程水平, Cjk是分类潜变量, 对于个体水平, θk是连续潜变量。在过程水平, 学生k在第j个步骤上对所有路径的作答[yjk1,…,yjki,…,yjkI]可以由分类潜变量 Cjk解释; 在个体水平, 学生对所有路径的最终作答[yk1,…, yki,…,ykI]可以由连续潜变量θk解释。根据方程(4), 在个体水平中, 从连续潜变量θk指向每条路径反应状态的箭头描述了能力 θk的变化对选择这条路径概率的影响, 对应于区分度参数(αi), 而从三角形指向每条路径的箭头θk表示为0时, 这条路径的选择概率, 对应于传统IRT模型的难度参数(βi)。

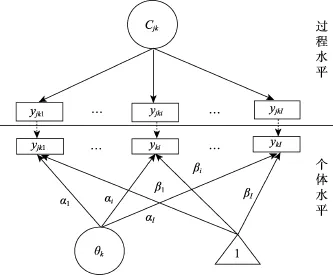
图1 本研究使用的MMixIRT模型示意图

3.2 参数估计的返真性与分类准确性

采用Monte Carlo模拟研究对本研究所采用的模型参数估计的返真性和分类准确性进行了检验。设计考虑2个影响因素：(1)过程水平的潜类别数(3个, 5个); (2)个体完成任务的过程步骤数(30步, 50步), 共2×2=4种实验条件。使用 R 语言自编程序,基于拓展MMixIRT模型产生每种条件下的反应数据 。 其 中 αi～ U （1,2 . 5）, βi～N （0,1）, θk～ N（0,1）(Wang, Xu, Shang, & Kuncel, 2018), 不同类别的反应概率参照Nylund, Asparouhov和Muthén (2007)的研究, 不同条件下各类别所占比例和题目(路径)答对概率真值见附录表1。每种条件下假设所有个体的过程步骤数相等, 其中最后一个步骤就是个体的最终作答状态, 用于估计个体水平的能力。每种条件下被试数固定为600人, 数据重复模拟100次。使用 Mplus 7.11 软件(Muthén & Muthén, 2005)估计模型的参数。

结果表明, 各参数返真性较好, 表现在各参数偏差都很小, 区分度参数均方误差(RMSE)在0.2左右, 难度参数 RMSE在0.1以下, 能力参数RMSE在0.3左右。各条件下模型分类结果的准确性较高,均在96%以上。

4 数据分析

4.1 题目

本研究使用的是PISA2012问题解决测验中一道交通问题的题目(Traffic CP007Q02)：地图上标明了每条路径所需的时间, 要求学生找到从Diamond到Einstein的最快路径。正确的最短路径需用时31 min,题目描述和路径标识如图2所示。

4.2 过程性数据编码

上述过程性数据来源于data source： http：//www.oecd.org/pisa/data/。首先, 筛选与有效路径点击有关的信息。然后, 将“路径选择的情况”按照不同路径进行拆分, 获得23条路径(P1, P2, P3…, P23)的点击结果。表1是整理后的数据格式示例, 每一行代表一个学生作答过程中的一个步骤, 每一列代表一条路径。其中, 0表示未选择, 1表示选择。例如,第一行表示编号为00017的学生在第1步选择P2,第二行表示第2步选择P1, 第三行表示第3步选择P13, ……, 第八行表示第8步取消P1……

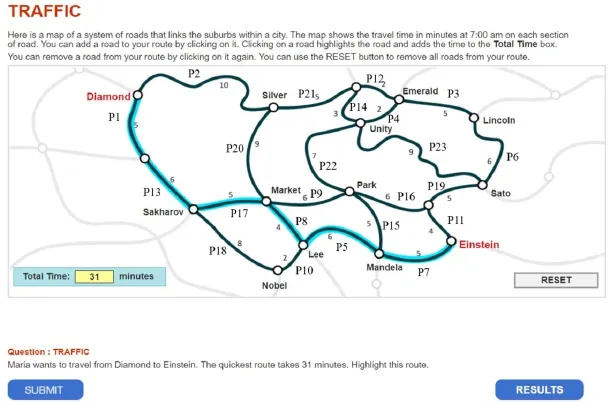
图2 PISA2012交通问题题目及其正确路径

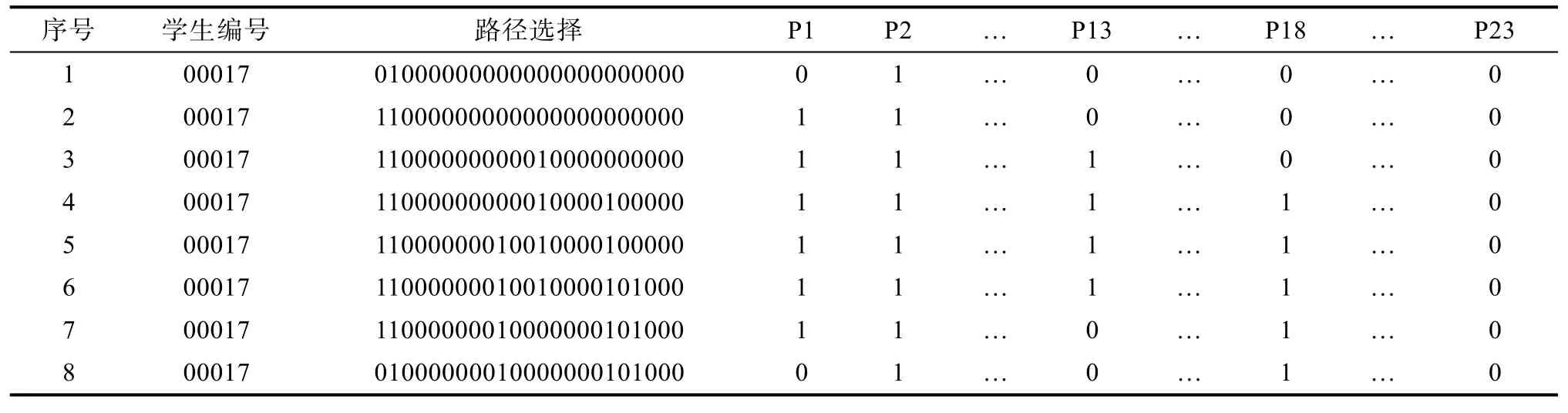
表1 整理后的过程性数据举例

之后按照答案重新计分。与传统试卷分析中的题目类似, 表1中的P1, P2, P3等23个变量代表23条路径。正确路径为：Diamond-Nowhere-Sakharov-Market-Lee-Mandela-Einstein, 即P1, P5, P7, P8,P13和 P17。对于过程中的每一步作答, 如果学生选择正确路径, 则该路径计分为 1, 否则计分为 0,同理, 如果选择了错误路径, 则该路径计分为 0,否则计分为1。编码后的23个变量命名为CP1, CP2,CP3,…, CP23。表2呈现了编码后的数据格式示例。例如, 第一行表示编号为00017的学生在第一步选择P2, P2为错误路径; 第二行表示第2步选择P1,P1为正确路径等。

4.3 样本

本研究样本来自 PISA2012问题解决测验中 5个地区的3196名15岁学生。其中加拿大、中国香港、中国上海、新加坡和美国的样本量分别为1449、433、411、456、406。5个地区共有139990条过程步骤, 学生的平均步骤数为43.80 (SD = 38.06), 其中最小值为1, 最大值为335。学生作答的平均反应时为669.22 s (SD = 543.12 s), 其中最小值为10.7 s,最大值为2384.7 s。

4.4 数据分析方法

采用拓展MMixIRT模型, 使用Mplus 7.11软件对策略类别和个体能力进行估计。采用关联规则挖掘探讨不同策略类别之间的关联。

关联规则挖掘的目的如下：若两个或多个变量之间存在某种规律性, 则它们之间存在关联, 关联规则挖掘就是寻找同一时间中不同出现项的相关性, 以求从大量的数据中抽取出隐含的信息。Apriori算法是一种常用的挖掘关联规则的频繁项集的算法, 其基本思想是从包含一个项的频繁项集开始, 递归地产生具有两个项的频繁项集, 然后依次递归, 直到产生所有的频繁项集(Peter, 2013)。本研究基于SPMF平台采用Apriori算法进一步分析学生问题解决策略之间的关系。

4.5 变量

使用学生问题解决过程中与作答时间有关的三个变量(路径点击数、重设数量、反应时)与模型估计结果的相关进一步验证模型估计结果的效度。其中, 路径点击数表示学生点击路径的数量; 重设数量表示学生取消前面所有路径点击状态, 重新开始做题的次数; 反应时表示学生完成任务所用的时间。同时, 研究还选取了耗时与正确作答时间的差异, 表示最后提交状态所选路径耗时与正确作答时间(31 min)差值的绝对值。

5 结果

5.1 模型选择

对于拓展的 MMixIRT模型的分析, 首先需要结合模型的拟合指标和潜在类别的可解释性(Rosato& Baer, 2012)确定分类的个数。表3给出5个地区数据同时估计得到的类别数为 1～7的模型拟合指标。采用的拟合指标包括loglikelihood、AIC (Akaike,1974)、BIC (Schwarz, 1978)、aBIC (Tofighi & Enders,2008)和熵(Asparouhov & Muthén, 2014)。其中, 前4个指标越小表示模型和数据拟合越好, 熵是用来测量混合模型区分各潜在类别的程度的指标, 该指标越接近 1表示类别区分越好。从结果可以看出,潜类别数量越多, 模型拟合越好。但是, 在 7个类别的情况下, 有2个类别的路径无法构成从起点到终点的完整路线。在6个类别的情况下, 有1个类别的路径无法构成完整路线。因此, 结合拟合指标的结果和类别的可解释性, 最终选择5个潜类别的结果。

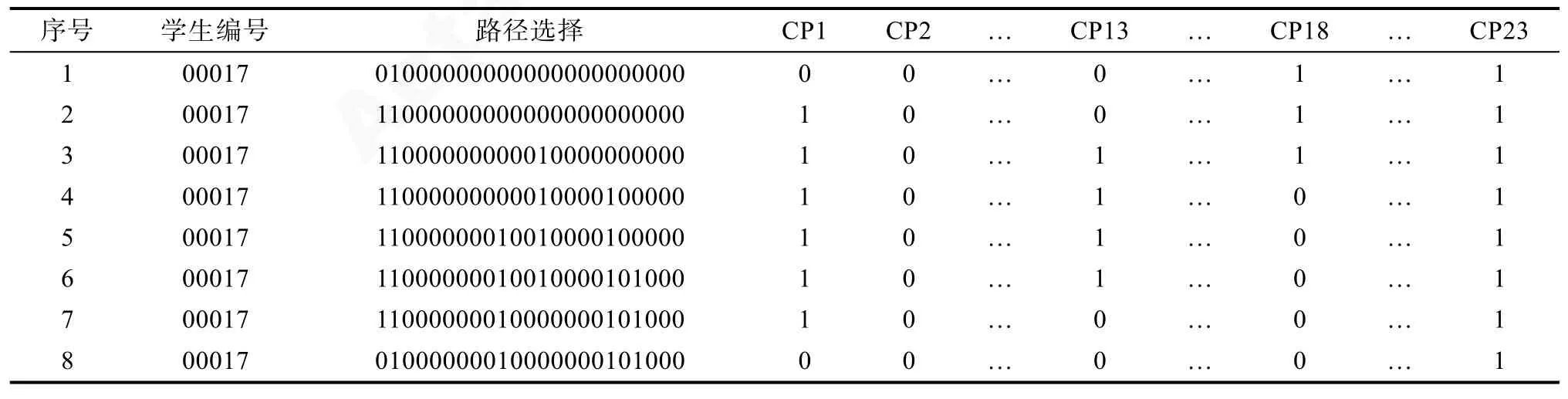
表2 编码后的过程性数据举例

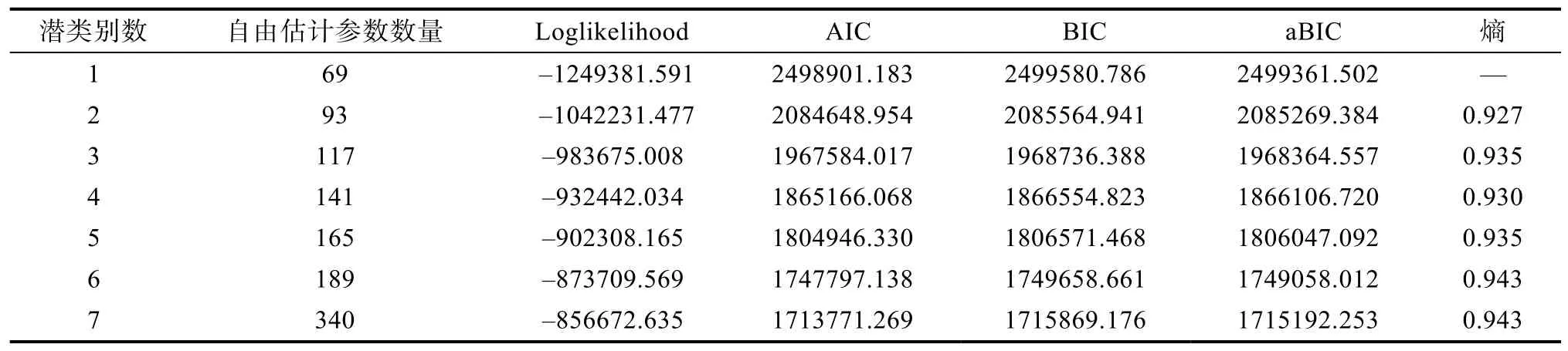
表3 模型拟合指标结果

5.2 策略类别特征及其与个体能力水平关系

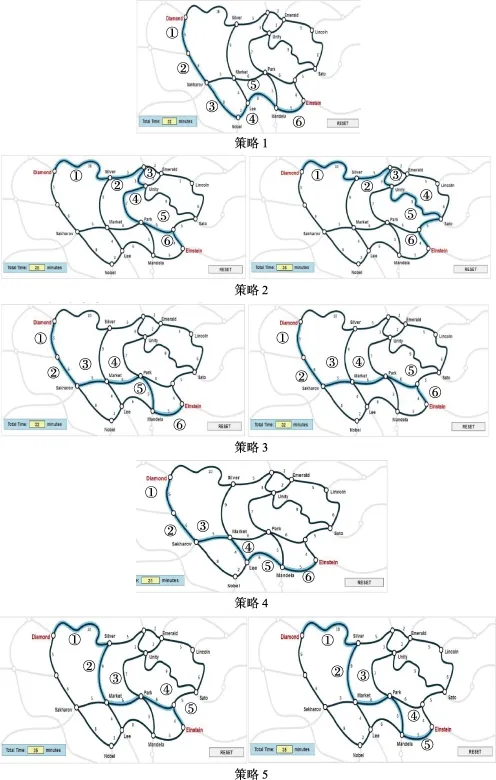
图3 各策略选择路径情况

拓展的MMixIRT模型可以将学生每一步过程操作后所处的状态分为5类, 各潜类别点击各路径的次数见附录表2。分析各类别选择频率最高的路径以及路径之间的关联, 可以形成这一类别的典型路径。各类别所选典型路线以及顺序如图 3所示,其中图中带圈的数字表示路径的顺序, 每个类别代表一种解决问题策略。因为学生的每次操作行为存在关联, 所以每次操作行为所属的类别也存在联系。如果相邻两步操作所属类别不同, 则学生使用的策略发生变化, 即存在策略转移。学生最后使用的策略与能力值有很高的相关, 如果使用正确策略,则会正确作答题目, 使用错误策略, 则会错误作答题目, 但是使用不同的错误类型策略, 能力值不同。

鉴于策略转移的存在, 我们将每个学生最后一步属于的策略作为其最终的策略, 分析不同策略下对应的能力估计值平均值, 得到5个策略对应的能力平均值分别为-0.714、-1.281、-0.714、0.399和-0.714。结合图3可以看出, 策略4与正确路径相同, 用时为 31 min, 个体的能力值也最高, 说明这是正确的策略; 策略 2所选路线是最远的路线, 与正确路径完全没有重合, 用时为35或36 min, 与正确路径作答时间差异最大, 个体的能力值最低, 说明这是最差的策略; 策略1、3、5与正确路径有部分重合, 这些策略虽然选择了不同的路径, 错误类型不一致, 但是其个体的能力值相等, 说明这些策略在优劣程度上差异不大。

表4呈现了各地区学生在这道题目上最后一步所用策略的分布情况。可以看出, 最后一步为策略4 (正确路径)的学生比例最高, 为策略2 (能力最低)的学生比例最低。从不同地区来看, 新加坡学生在最后一步上使用策略4的学生比例为81.6%, 略高于其他地区, 说明新加坡学生在这道题上表现最好,而美国学生在最后一步上使用策略4的学生比例为75.6%, 略低于其他地区, 而最后一步采用策略 2的比例都高于其他地区, 说明美国学生表现相对较差, 这与个体能力水平估计的均值结果是一致的。另外, 不同地区错误组学生在最后一步使用的策略上呈现出不同的特点。例如, 加拿大学生较多使用策略 3, 新加坡和中国上海学生较多使用策略5和3, 而美国学生较多使用策略1, 中国香港学生较多使用策略1和3。

5.3 策略应用情况

为了探讨过程数据中策略的变换, 研究将学生在过程中连续使用某种策略3次或以上定义为明显使用了该种典型策略。在描述策略转换中只记录了不同策略之间的转换, 如果转换过程中同样的策略出现了多次, 只记录最后一次转换。表5呈现了各地区正确组和错误组学生在解题过程中应用策略数的情况。总体来看, 正确组学生在解题过程中应用策略数为4和5的情况最多。正确组学生中应用5种策略的人数比例明显大于错误组。说明在正确组中, 有接近三分之一的学生是通过尝试所有5种策略才找到正确路线。而错误组有超过三分之一的学生尝试了4种策略即停止作答, 提交了错误的路线。从各地区比较来看, 新加坡和美国正确组应用5种策略的学生比例低于其他地区, 其中美国最低。

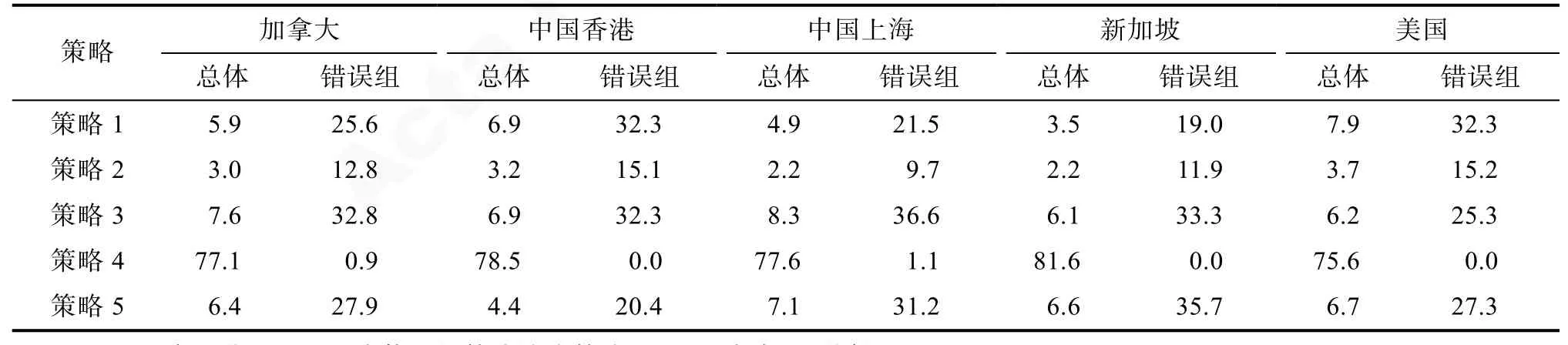
表4 各地区学生解题最后一步所用策略分布比例(%)

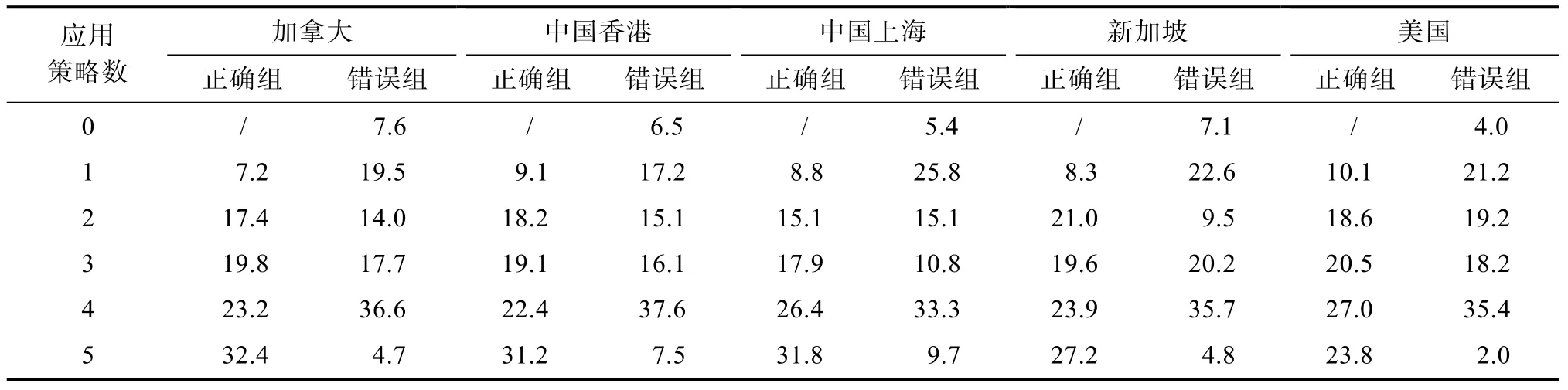
表5 各地区问题解决过程应用策略数分布比例(%)

为了进一步分析策略之间的关系, 表 6和表 7呈现了 Apriori算法的关联分析结果。频繁项集指频繁同时出现的两种策略, 频次表示这两种策略同时出现的次数。置信度是指包含前项和后项的事务个数在包含前项的事务总数中的比例。例如, 5==>1表示同时使用策略1和策略5的学生人数占使用策略5学生人数的比例。根据表9结果可以看出, 在正确组学生的策略使用规则中, 策略3和5, 策略3和4, 策略2和5, 策略1和5具有较强的关联关系。例如, 对于使用策略 5的学生来说, 同时使用策略3的概率为 0.51。与正确组学生不同的是, 错误组学生的策略使用规则中, 策略3和4存在较弱的关联, 即错误组学生能够将策略3转换到使用正确策略4的概率较低。另外, 对于使用策略5的学生来说, 使用策略3的概率明显低于正确组学生。根据表7可以看出, 各地区正确组和错误组学生使用策略规则基本一致, 但是中国上海的正确组学生表现出不一致的策略使用规则, 具体来讲, 使用策略 2的学生使用策略5的概率、使用策略3的学生使用策略5的概率明显高于其他地区; 使用策略4的学生使用策略3的概率、使用策略3的学生使用策略4的概率明显低于其他地区。

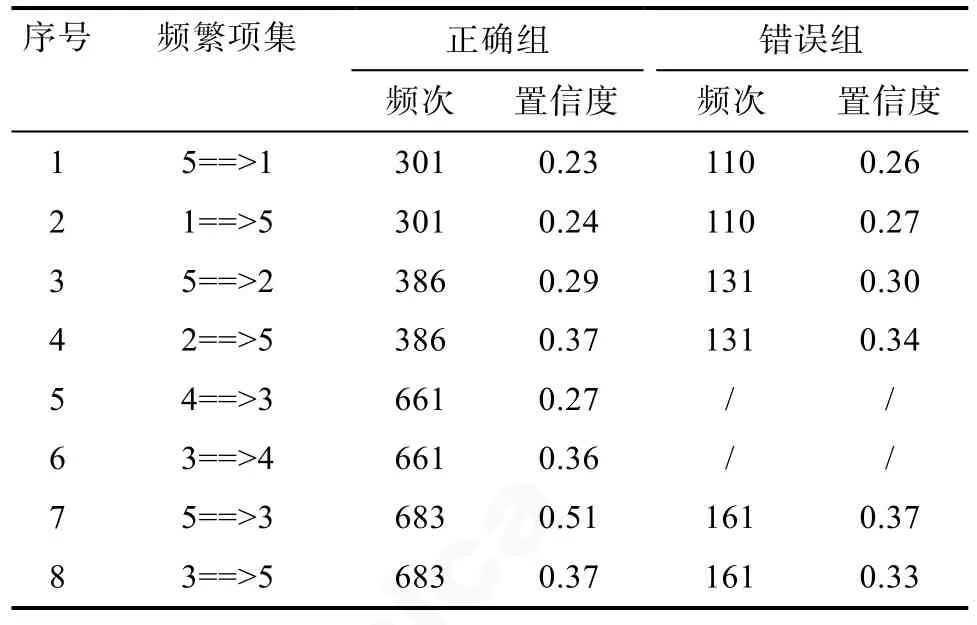
表6 学生总体应用策略之间的关系

5.4 过程性变量和能力的关系

表8呈现了路径点击数、重设数量、耗时与正确作答时间的差异、反应时这些过程性变量以及个体能力值的描述性统计指标, 及过程性变量与个体能力值的相关。从表8中可以看出, 对于所有地区,正确组的路径点击数小于错误组, 正确组的重设数量小于错误组, 正确组和错误组的反应时没有显著差异。耗时与正确作答时间的差异越大, 个体能力估计值的平均水平越低。另外, 结果还反映了不同地区在完成题目过程中的特点。从描述统计方面来看, 各地区呈现出了不同的典型特征, 例如, 美国学生个体能力估计值的平均水平最低, 路径点击数最少, 错误组耗时与正确作答时间的差异明显大于其他地区; 而新加坡学生个体能力估计值的平均水平最高, 但是平均反应时也最长。

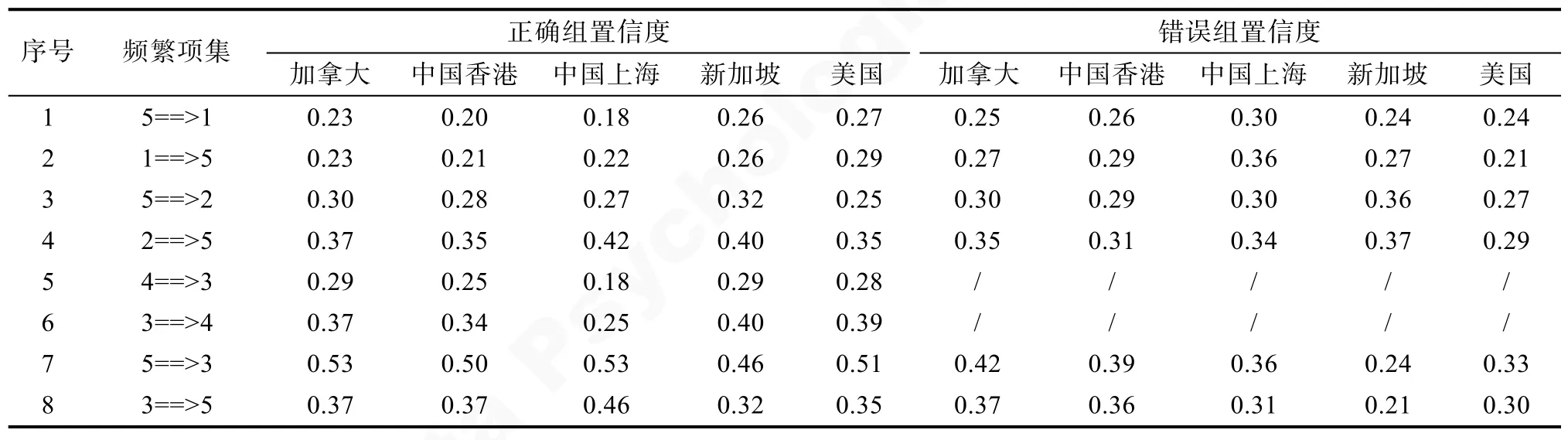
表7 各地区学生应用策略之间的关系

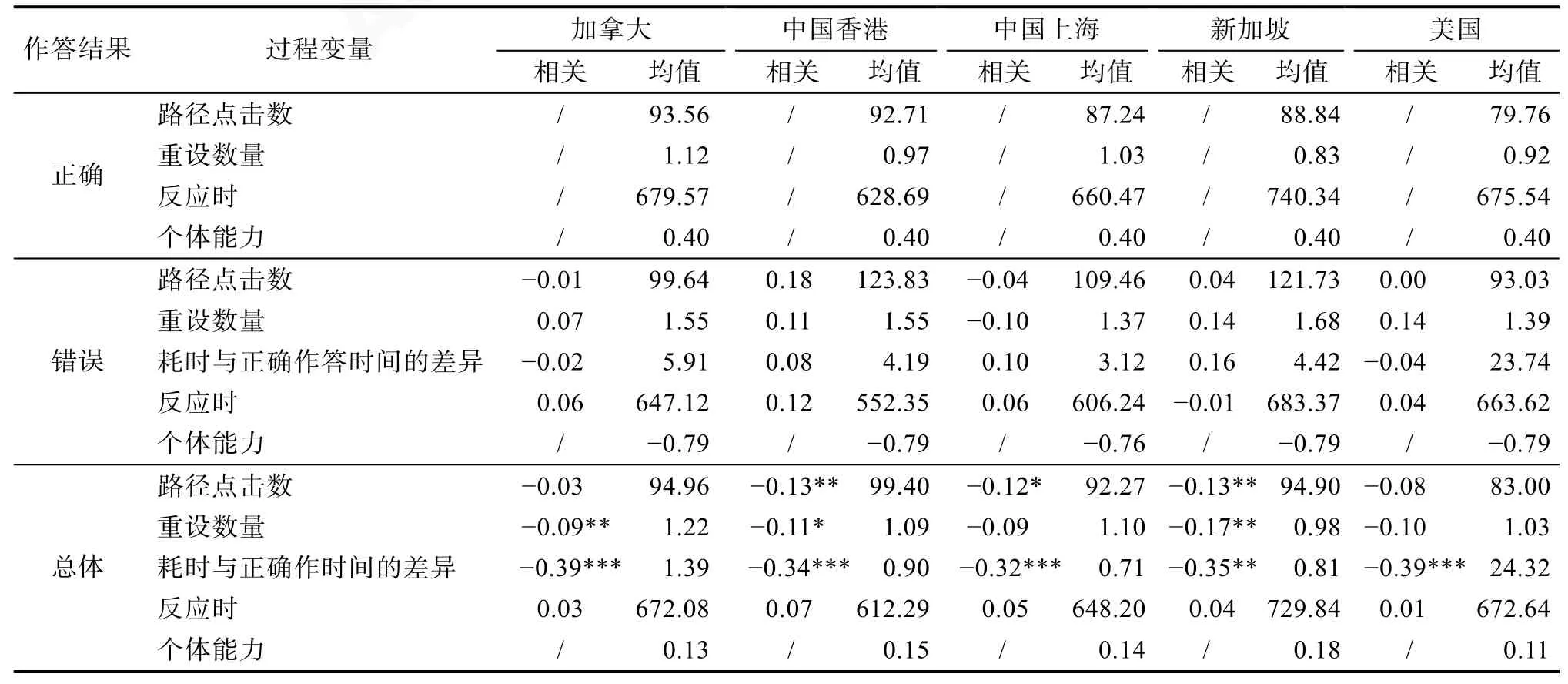
表8 过程变量的描述统计及其与个体水平能力估计值的相关

6 讨论与结论

拓展的MMixIRT模型结合了IRT模型、潜类别模型和多水平模型的特点, 不仅可以在过程水平分析策略类别特征, 而且还可以在个体水平估计能力值。在过程水平, 使用潜类别模型确定学生解题的过程策略, 深入探讨策略应用的情况; 在个体水平, 使用IRT模型估计学生的个体能力值。模型优势在于能够同时描述过程水平和个体水平的信息。过程水平中的策略分析能够得到不同群体在问题解决过程中的典型行为模式和思维特点, 从而更好地为提高学生的问题解决能力提供有针对性的信息。另外, 拓展 MMixIRT模型具有良好的参数返真性和较高的分类准确性, 能够应用于过程性数据的分析。

研究将拓展的MMixIRT模型应用于分析5个地区学生完成问题解决题目的过程性数据, 验证了该模型结果的合理性和可解释性。首先, 操作步骤特征可分为5种策略, 体现了问题解决过程中不同能力水平学生的特征。策略 4是正确的解题策略,最后一步为策略4的学生比例越高, 平均能力水平也越高。策略2是距离正确路径最远, 耗时最长的策略, 即最差的策略。最后一步为策略2的学生比例越多, 平均能力水平也越低。其次, 关于策略应用和转换的结果体现了学生解决问题过程中试误策略的应用, 这与现实中问题解决策略的使用一致。在正确组中, 学生在解题过程中应用策略数为4次、5次的情况最多, 说明学生通过不断转换策略完成题目, 很少有学生只使用一种正确策略直接解决了问题。另外, 最典型的正确组学生策略使用规则是从策略3转换到策略4。也就是学生先选择了与正确路线重合的前三条路径, 然后在下一条路径上, 没有选择从Market到Lee, 而是从Market到了Park (见图3, 后面三条路径的用时加起来为16 min,大于正确答案后三条路径的用时15 min。然后学生可能发现存在比这样走用时更短的路线, 于是从策略3转换到了策略4, 即从Market改为走向Lee, 从而选择了正确答案的路线。而在错误组中, 学生在解题过程中应用策略数为4的情况最多, 但是较少的学生坚持尝试了5种策略。最后, 操作过程变量与策略和能力之间关联分析的结果, 证实了这一模型分析过程数据的有效性。部分过程性的变量与个体的问题解决能力有显著相关, 结果表明, 除过程中学生策略选择外, 其他过程变量(例如, 路径点击数、重设次数等)也均在不同程度上与学生的问题解决能力存在相关。

研究还关注了不同地区间过程水平和个体水平分析结果的比较。首先, 各地区在过程性变量上呈现出不同的特点, 例如, 美国学生问题解决能力最低, 路径点击数最少, 错误组耗时与正确作答时间的差异明显大于其他地区, 而新加坡学生问题解决能力最高, 反应时也最长。从文化差异上来看,西方文化背景下学生关注个人价值以及个体的好奇心和兴趣, 而儒家文化背景下学生关注个体努力程度, 他们认为努力是实现成功的必备因素(Li,2012)。此题考查的是问题解决的计划与执行部分,如果学生不断努力试错, 也可以得到正确答案。努力程度(工具性动机)会促进学生问题解决的表现。这也可能是新加坡、中国上海、中国香港学生的问题解决能力较高的原因。而新加坡学生问题解决表现最好, 主要源于新加坡的整体课程设计注重学生的问题解决能力, 将问题解决能力系统纳入课程,例如, 其在中小学数学大纲中在数学过程部分, 明确列出了思维技能和问题解决策略(Fan & Zhu, 2007)。因此, 在策略使用上, 新加坡正确组应用 5种策略的学生比例明显低于其他地区, 说明新加坡学生解决问题典型特征是思考时间比较长, 使用策略数相对较少而得到正确答案。而美国学生正确组应用5种策略的学生比例也较低, 解决问题典型特征是思考时间比较少, 但是并未像其他地区一样, 去尝试足够多的策略最终得到正确结果。其次, 加拿大、中国香港、中国上海、新加坡错误组学生在最后一步较多使用策略 3。从策略应用的结果可以看出,很多作答正确的学生都是从策略 3转到了策略 4,说明对这些解题错误的学生, 如果再给予更多的思考时间, 有很大的可能最终转换为正确的策略。这些结果可以为教学和训练提供更加丰富的信息, 帮助教师给予有针对性的指导。综上, 过程性数据分析的结果一方面能够给教育测量研究者和测验题目研发者提供更多信息, 以便进行命题改进, 另一方面, 这些信息还可以被纳入测验计分体系, 测验计分不再只基于学生个体的最后作答, 而结合了学生策略的使用, 这将在一定程度上丰富测验分数的含义。

拓展的 MMixIRT模型比较灵活, 可以在实际中结合题目的特点和关注的重点定义不同的模型。首先, 可以在模型的个体水平中加入描述学生类别特征的潜类别, 也可以考虑在过程水平中加入描述步骤能力的连续潜变量, 探讨学生在解题过程中能力的变化情况(Liu, Liu, & Li, 2018)。其次, 还可以在模型加入能够减少测量误差并能预测学生问题解决能力的其他协变量, 例如学生的动机等(Fox &Glas, 2003)。最后, 本研究为单任务情境, 当分析对象为多任务时, 可以将其拓展为三水平模型, 分别为过程水平、任务水平和个体水平, 同时考察不同任务情境问题解决策略的应用以及多任务情境下个体能力估计。

本研究具有一定的局限性。首先, 在策略转换分析时, 将使用某种策略3次或以上定义为使用了该种典型策略, 这样的定义也损失了一部分不稳定的策略转换的信息。如果这种不稳定的策略转换也是考察的对象, 可以将这些信息纳入策略转换的分析中。其次, 分析过程中只是将单一的路径作为分析的单元, 没有考虑可能的路径组合(如某些情况下, 不同路径之间的链接是唯一的, 可能将这些路径合起来分析更加合理), 可以在未来的研究中考虑不同路径组合转换的模型。另外, 这一模型在复杂问题解决过程中的普适性尚待进一步检验, 使用MMixIRT模型的前提是需要将过程性数据编码为类似本研究中的数据结构, 实际中可能某些任务不太容易实现这样的编码转换。

研究得出的主要结论如下：

第一, 拓展的 MMixIRT模型不仅可以基于行为序列分析学生解题过程中策略使用情况, 还可以在个体水平上提供能力估计值。

第二, 使用拓展的 MMixIRT模型可以对不同地区学生在解决问题时策略使用情况的典型特征进行分析, 为有针对性的训练提供参考。

附表1模拟研究中各类别数量比例及题目答对概率

注：此处的题目答对概率是指除去最终作答状态的所有过程步骤的概率, 真实值中最终作答状态的分类与各潜在类别的特征一致。

潜类别数为3潜类别数为5题目 类别1(33.33%)类别2(33.33%)类别3(33.33%)类别1(20.00%)类别2(20.00%)类别3(20.00%)类别4(20.00%)类别5(20.00%)1 0.85 0.85 0.10 0.85 0.85 0.10 0.10 0.10 2 0.85 0.85 0.20 0.85 0.85 0.20 0.20 0.20 3 0.85 0.85 0.10 0.85 0.85 0.10 0.10 0.10 4 0.85 0.85 0.20 0.85 0.85 0.20 0.20 0.20 5 0.85 0.85 0.10 0.85 0.85 0.10 0.10 0.10 6 0.85 0.85 0.20 0.85 0.10 0.85 0.20 0.20 7 0.85 0.85 0.10 0.85 0.20 0.85 0.10 0.10 8 0.85 0.85 0.20 0.85 0.10 0.85 0.20 0.20 9 0.85 0.85 0.10 0.85 0.20 0.85 0.10 0.10 10 0.85 0.85 0.20 0.85 0.10 0.85 0.20 0.20 11 0.85 0.10 0.85 0.85 0.20 0.20 0.85 0.10 12 0.85 0.20 0.85 0.85 0.10 0.10 0.85 0.20 13 0.85 0.10 0.85 0.85 0.20 0.20 0.85 0.10 14 0.85 0.20 0.85 0.85 0.10 0.10 0.85 0.20 15 0.85 0.10 0.85 0.85 0.20 0.20 0.85 0.10 16 0.85 0.20 0.85 0.85 0.10 0.10 0.10 0.85 17 0.85 0.10 0.85 0.85 0.20 0.20 0.20 0.85 18 0.85 0.20 0.85 0.85 0.10 0.10 0.10 0.85 19 0.85 0.10 0.85 0.85 0.20 0.20 0.20 0.85 20 0.85 0.20 0.85 0.85 0.10 0.10 0.10 0.85

附录2每个类别点击各路径的次数

路径 类别1 类别2 类别3 类别4 类别5 路径 类别1 类别2 类别3 类别4 类别5 P1 31050 1010 26185 10450 1175 P13 26422 535 27272 10874 276 P2 358 20917 272 71 26673 P14 70 12160 120 23 197 P3 14 4771 10 4 10 P15 766 1131 5969 345 4394 P4 16 1942 45 10 12 P16 740 3933 11056 158 9578 P5 10752 320 396 8981 4465 P17 836 430 28099 11113 785 P6 33 3751 24 17 19 P18 17576 266 374 64 157 P7 7554 1027 4109 6684 7135 P19 97 6384 196 11 549 P8 1082 241 433 11053 4972 P20 136 575 374 91 20809 P9 860 800 22245 154 14474 P21 80 21507 179 22 360 P10 15100 380 728 259 394 P22 60 5906 286 0 730 P11 1468 6723 7752 477 9474 P23 12 5436 120 2 6 P12 27 7128 33 10 84