混合机械加工过程的偏差网络建模与误差溯源

祝 鹏, 余建波+, 郑小云, 孙习武, 王永松, 陈长江

(1.同济大学 机械与能源工程学院,上海 201804；2.上海航天设备制造总厂有限公司, 上海 201100)

0 引言

在智能制造环境下，混合式多阶段加工系统已被广泛应用。复杂零件往往需要经过多道工序的加工，因此会受到不同工序上制造误差的影响。在每道工序上又因为误差的来源不同(如机床、夹具、刀具)，且误差以加工特征为载体在不同工序间的累积、传递和演化，使得各种偏差最终反映为成品零件的质量问题。同时，为了满足生产线运作可靠性与足够的生产柔性，往往在一道工序上布置多台机器共同加工，从而构成了复杂的串并联混合式多阶段的自动化加工过程。最终，导致零件质量在加工过程中会受到多个误差源的综合影响。因此，对多源多工序混合式加工过程的零件尺寸偏差流进行建模与控制，从而在智能制造环境下提高产品的加工质量具有重要意义。

当前对多工序加工系统的质量控制研究主要集中于解决串行制造系统的偏差传递问题。自Hu等[1]提出偏差流(Stream of Variation, SOV)理论以来，相关方法主要在车身装配质量控制问题方面得到应用，因其能够对多阶段制造过程中的偏差传递、耦合和传递机理进行有效的描述，而后又被广泛应用于制造系统加工[2-3]和装配[4-5]过程的误差建模与分析。Cunningham等[6]通过运用矩阵的齐次变换来描述工序间的误差传递，通过分析各加工要素(夹具、刀具、机床等)以及定位基准偏差对加工件的影响，建立误差传递的状态空间模型，为多工序的加工误差溯源过程奠定了基础。Jin等[7]首次提出基于状态空间模型的刚体零件在平面内因运动造成的尺寸偏差建模方法。Ding等[8]对文献[7]的模型进行了扩展，提出了一个集成产品设计信息和工艺信息的公差合成的建模方法，为产品的偏差流分析提供了有效途径。王小巧等[9]将状态空间模型和粒子群优化算法结合提出了一种针对复杂机械产品多阶段装配过程的质量监控系统。文献[10]对基于状态空间模型的多阶段偏差流控制方法进行了综述。以上研究虽然对多工序的装配过程建立了通用有效的模型，但是这些研究都是针对单个偏差流的控制，对多偏差流误差间的相互影响未加考虑。此外，由于混合式多阶段加工过程的多个偏差流会相互影响，而状态空间模型求解过程中需要对不同的坐标数据进行转换，混合式工艺的复杂性会导致数据在转换过程中失真严重，运算复杂且计算量大，状态空间模型并不适用于混合式多阶段加工过程。

Du等[11]将状态空间模型与偏差流理论相结合并应用于串并联混合式多阶段制造系统。但状态空间矩阵维数过高，计算过程复杂，降维易导致数据失真，难以运用到实际生产检测中。刘道玉等[12]针对复杂产品的质量控制问题，提出一种关键特征的提取方法与传感网络构建方法，为数字化加工的质量控制提供了新思路。复杂网络(complex networks)模型[13]能够清晰地描绘出各种复杂系统的结构特征和拓扑结构，且通常具有小世界特性，符合生产系统中工序内联系紧密，而工序间相对稀疏的特性，因此，运用复杂网络对生产加工过程建立网络模型具有合理性与可行性。目前，复杂网络已经广泛地应用于舆情分析，疾病控制以及复杂制造系统中的质量控制。Liu等[14]针对波动源识别问题，提出一种基于加工误差传播网络的波动评价和识别方法，建立了工艺流程的波动传递方程，从而识别需要优先进行改进的工序和加工要素。贾峰等[15]针对多工序加工过程运用复杂网络构建了误差传递网络模型，并结合控制图以实现对加工质量波动的量化分析与评价。Jiang等[16]建立了一种基于神经元模型的加工误差传递网络，该模型用反向神经网络求解，实现对多阶段加工过程的实时监测检测。郑小云等[17]对混合式多阶段加工过程运用了复杂网络进行了误差传递网络建模与溯源，通过用PageRank排序算法以及分层回溯算法有效识别了复杂加工过程误差网络中的关键节点和误差源。彭开香等[18]对复杂工业过程质量相关的故障检测与诊断技术作了综述，详细梳理了相关质量检测中的典型方法的基本思想和改进过程。但这些研究均针对单个偏差流的误差传递进行建模与分析，而对混合式加工多偏差流传递问题有待深入研究，特别是针对混合式加工多偏差流故障溯源问题未有效展开。

本文针对混合式多阶段加工系统，运用复杂网络相关理论与方法，提出了加权自调节偏差传递网络建模方法与异常源遍历回溯算法，解决了复杂制造系统多偏差流的建模、评价、识别等问题。本文主要贡献如下：①根据混合式加工工艺过程之间的相互关系将抽象的节点连接为偏差传递关系网络，并将质量特征抽象为权重，构建多偏差流加权自调节偏差传递网络；②提出了基于加权LeaderRank算法的网络关键节点(关键加工特征、加工要素)识别算法，提取出易导致产品质量失控的关键加工表面；③提出基于遍历回溯算法的误差溯源方法，识别误差传播关键路径，并提出误差源节点判别指标——ContributionIndex，识别系统的关键误差源；④以典型的具有混合式加工过程的主轴承盖为实例进行分析，验证了本文所提方法的有效性。

1 混合式多阶段加工过程的复杂网络建模与误差溯源方案

在混合式多阶段加工过程中，零件的尺寸精度不但受到多源和多道工序上误差的影响，而且不同工序上的误差流也会交叉影响。而在工序层面上，考虑到加工工艺的先后关系，加工特征会被多次加工，因此加工特征间存在基准和演化的关系，误差在各道工序间传递、累积并最终反映到成品上。复杂网络有向图能对这类基准、累积、演化的关联关系加以描述，形成偏差传递关系网络，因此混合式多阶段加工系统可抽象为一个复杂网络系统。在偏差传递关系网络基础上，根据实际加工工艺信息和质量特征信息建立加权自调节偏差传递网络模型，来反映不同偏差流上误差大小及其传递路径。

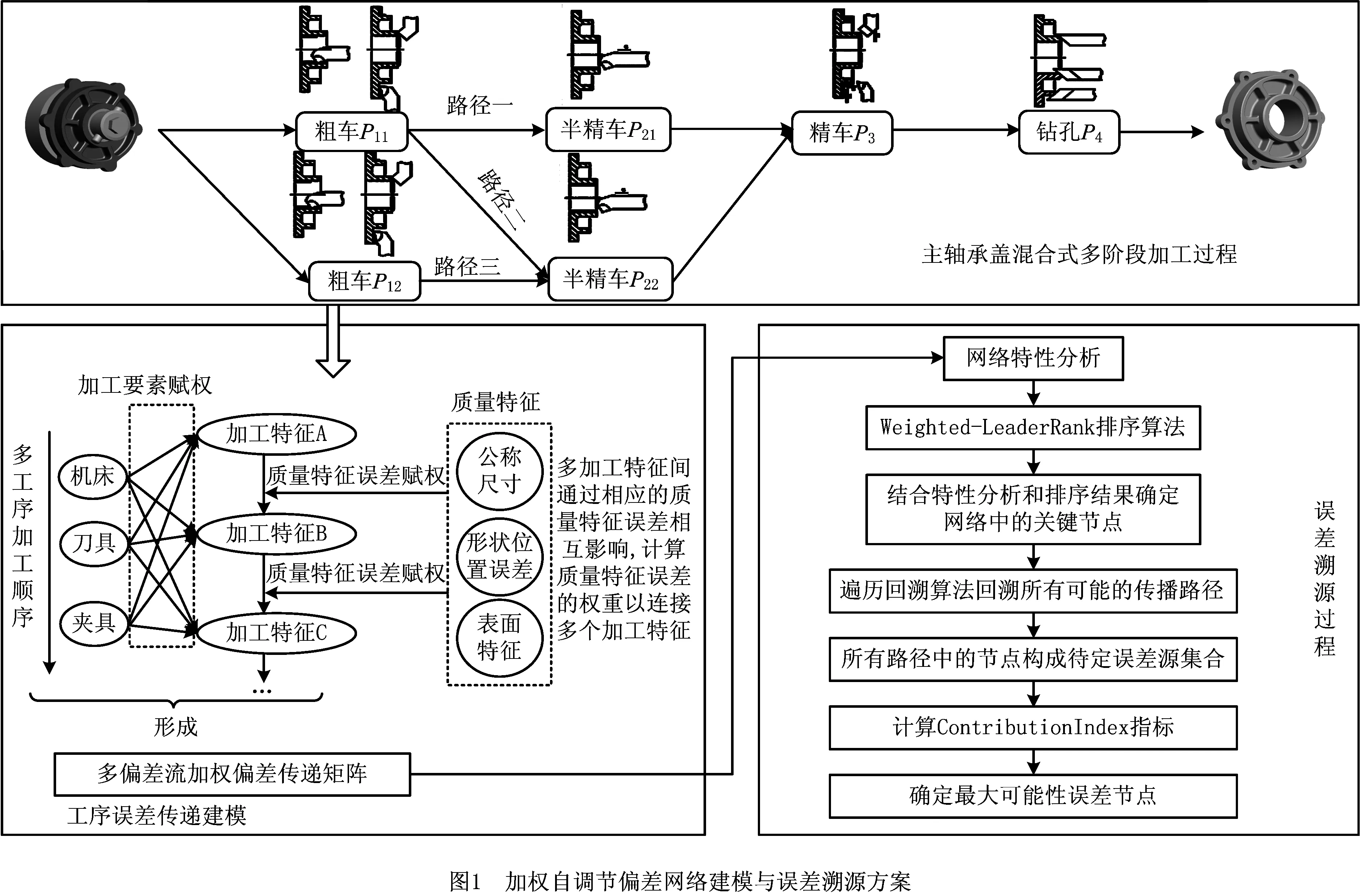
如图1所示为加权自调节偏差传递网络建模和误差溯源的方案图。如图1上半部分所示，串并联混合式加工系统是由不同的工艺路线叠加而成的复杂网络，该网络中节点为各种加工要素和加工特征，而节点间的连接方向则由工艺路线中工序的先后关系确定。因此，复杂网络可对这样的复杂系统进行一种有效的抽象描述与建模。首先提取加工过程中的加工要素和加工特征(如加工圆面，平面，孔，槽等)作为网络中的节点。根据加工工艺信息连接各个节点。多加工特征之间通过质量特征相互影响，计算两加工特征间的质量特征误差，将其作为连接加工特征间的误差权重。因此，整个包含多加工特征节点的误差网络得以建立。 通过对建立的网络进行特性分析并用加权LeaderRank算法排序识别加工过程中的关键节点，最后采用遍历回溯算法确定误差传播路径并用ContributionIndex指标对待定误差源节点进行计算，识别关键误差源。

2 加权偏差传递网络与误差溯源

2.1 加权偏差传递网络建模

基于复杂网络构建的加工误差传递关系网络结构通常难以描述复杂动态的误差传递，在该关系网络中只包含了代表加工要素和加工特征的节点，以及节点之间的连接关系。实际加工过程中误差在工序间传递的强度有差异，因此提出加权自调节偏差传递网络模型，将不同节点之间的误差影响通过权重体现出来，从而可对实际加工过程中的误差传递信息和网络的动力学演化特征进行全面精确的描述。

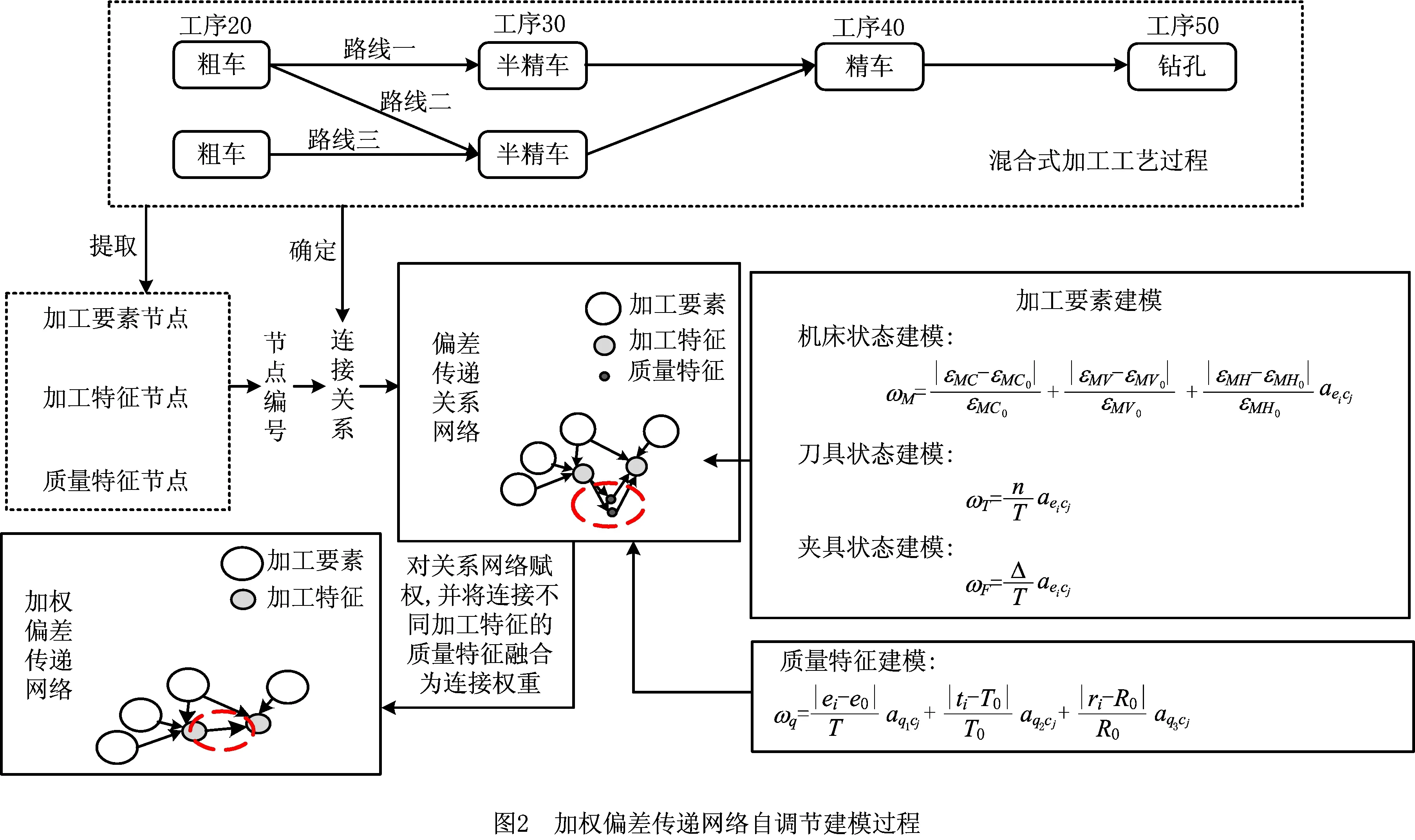
将复杂网络相关理论引入混合式多阶段加工过程中，依据零件加工工艺确定零件节点以及连接关系，采用有向图方法，形成偏差传递关系网络。最后，分别对各加工要素和质量特征进行建模，结合底层加工信息对关系网络进行赋权，建模过程如图2所示，具体实施步骤如下：

步骤1提取网络节点，确定连接关系，建立偏差传递关系网络。

具体的网络连接关系分为3类，即从加工要素到加工特征、加工特征到质量特征和质量特征到加工特征，如图3a所示。图3b为偏差传递关系网络映射图，描述了3种类型节点之间的关系。加工特征是零件加工的基本单位。每一个加工特征本质上又是由多种质量特征所描述的，因此加工特征间的相互影响可以转化为两者间的相关质量特征的相互影响。

质量特征分为3类，包括公称尺寸，形状与位置公差和表面特征误差。对于加工要素和加工特征连接而成的网络可以表示为Gec={Ve,Vc,aeicj}，式中：Ve={ve1,ve2,ve3,…,ven}表示所有加工要素的集合，n表示加工要素的个数；Vc={vc1,vc2,vc3,…,vcm}表示所有加工特征的集合，m表示加工特征的个数；Ve,Vc表示加工要素节点指向加工特征节点的有向边；aeicj表示边Vei,Vcj的初始权重，若两节点间存在连边，aeicj=1，否则aeicj=0。对于加工特征和质量特征连接而成的网络可以表示为Gcq={Vc(q),Vq(c),aciqj(qjci)}，其中Vc和Vq分别为加工特征和质量特征节点的集合，节点间有连边则初始权重aciqj都设为1，没有边连接则设为0，由此可以形成完整加工过程的有向关系网络。

步骤2确定加权自调节偏差传递权重因子。

在偏差网络的误差建模中，权重因子的确定是可以自调节的，如机床的误差种类，以及质量特征综合误差的权重因子的确定，均可以根据生产线要求或专家意见在合理范围内调节。

(1)机床误差εM机床回转误差是影响机床加工精度的重要原因，因此本文以机床主轴回转误差εMC，垂直度误差εMV和平行度误差εMH为主要判别因素。具体误差种类的取舍可根据产线情况自行调节，综合后作为机床误差的权重。

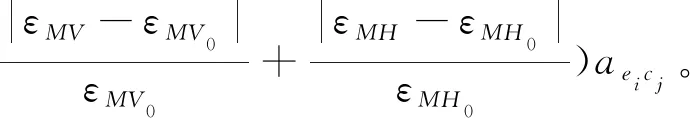
(1)

式中：εMC0表示主轴允许的最大回转误差，εMV0表示主轴允许的最大垂直度误差，εMH0表示主轴允许的最大水平度误差。

(2)刀具误差εT本文以刀具磨损情况来反映刀具的误差。通常刀具有刀具使用磨损限度，当刀具磨损量达到磨损使用限度时则不能继续使用，需要重磨。磨损量可以通过直接测量得到。因此本文采用刀具磨损量与磨损限度的比值反映刀具误差，作为刀具的误差权重因子：

ωT=εTaeicj。

(2)

式中εT=/L，其中表示刀具当前磨损量，L表示刀具设计时的使用磨损限度。

(3)夹具误差Δ夹具误差通常包括夹具的制造误差和定位误差，本文将夹具的误差定义为实际零件的定位位置与理想位置的偏差。因此确定夹具的误差偏差权重因子：

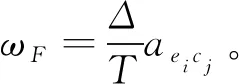
(3)

式中：Δ表示夹具定位后的绝对误差，T表示被夹持的几何特征的尺寸的公差带宽。

(4)质量特征综合误差 零件的加工特征误差可通过该特征对应的质量特征反映出来，而其质量特征又影响与之相关的加工特征。因此，加工特征间的误差影响是通过质量特征传递的。为了获得加工特征间的误差权重，在零件加工过程中采用质量特征误差赋予网络加工特征节点之间的权重[19]，如图2中两个局部网络图中的虚线阴影部分。该建模方法虽然在一定程度上增大了误差溯源的粒度，却在网络建模难度与溯源精度上有较好的平衡，当确定误差源是某个加工特征后只需人工对该加工特征对应的3种质量特征误差进行分析即可，具有较高的实际应用价值。由于不同的加工特征间往往只会通过其中的某种质量特征相互影响，下文中的式(4)～式(6)是不同的质量误差类型，可以用式(7)统一描述不同加工特征间的权重因子。

公称尺寸描述了零件的控件位置尺寸，如长度、直径、高度等。由于各个质量特征的误差是经加工实测数据计算得出的实际误差，不考虑其方向性，采用绝对值进行计算，将其作为衡量加工特征间误差传递大小的一个指标，余同。

(4)

式中：ei为零件的实际尺寸，e0为零件的额定尺寸，T为公差，aqkj(k={1,2,3}，1为尺寸误差，2为形位误差，3为表面特性误差)为连接关系，若质量特性节点Vqk与加工特征节点Vj有连接则aqkj=1，否则aqkj=0，余同。形状与位置公差描述了零件尺寸偏差，以及加工特征之间的相互位置偏差。

(5)

式中：ti表示实际形位指标，T0表示加工的形位要求。表面特征描述了零件加工表面的粗糙度、热处理特性等。本文以主要因素粗糙度误差作为表面特征误差。

(6)

式中：ri表示实际加工表面粗糙度，R0表示加工粗糙度要求。最终的加工特征之间权重因子为：

ωq=ω1εq1+ω2εq2+ω3εq3。

(7)

式中：ω1，ω2，ω3分别代表3类误差的权重系数，具体大小由专家打分来为权重系数赋值，以实现多偏差流的复杂网络自调节建模。本文中无特殊需求，因此将ω1：ω2：ω3取值为1:1:1，最终得到质量特征综合误差。

步骤3为偏差传递关系网络赋权，建立加权偏差传递网络。

结合底层加工测量数据，运用步骤2中的计算方法，对步骤1中的关系网络进行赋权。由此，整个加权自调节偏差传递网络得以建立，整个网络可以描述为G={V,E,W}，其中：V={v1,v2,v3,…,vn}为网络节点集，包括加工特征节点和加工要素节点，n表示网络中节点的个数；E={e12,e13,e1n…,eij,…,en(n-1)}为节点的连边，表示误差的传递方向；W={ω12,ω13,ω1n,…,ωij,…ωn(n-1)}表示网络节点连边的权重。为了计算方便将该网络转化为矩阵形式。

2.2 关键加工质量特征识别

复杂网络的关键节点是指相比网络中的其他节点，能够在更大程度上影响网络的结构与功能的一些特殊节点，通常对应于零件的关键加工特征。对于混合式加工过程的复杂网络，其中的关键节点往往具有较大的度或在传播路径中处于关键位置，通过对关键节点的控制能够有效保证生产线上产品质量的稳定。因此识别误差传递网络中影响网络性能较大的关键特征节点具有重要意义。

首先对建立的加权自调节偏差传递网络进行特性分析。基本特性分析包括节点度、度分布、平均路径长度、簇系数等，以及对应到加权偏差传递网络中相应的特性分析，反映了不同类型网络中各个节点的偏差传递效应。再结合加权LeaderRank排序算法，确定网络中的重要节点。表1中介绍了复杂网络特性[20]的计算方法。

本文借鉴加权LeaderRank排序算法，该算法是谷歌页面排序算法PageRank的优化算法。加权LeaderRank算法不但比PageRank的适用范围更广，能用于加权有向网络，而且算法解决了PageRank中随机跳转概率相同以及算法中的参数q的选取往往需要试验获得，并且在不同的背景下最优参数不具有普适性的问题。相比PageRank，该算法收敛更快，能更好地识别网络中有影响力的节点，挖掘出重要的节点能够将网络流传播的更快更广，并且在抵抗垃圾用户攻击和随机干扰方面有更强的鲁棒性。

该算法通过添加一个背景节点以及该节点与网络中所有节点的双向边来代替PageRank中的跳转概率q。背景节点同样保证了网络的强连通性。下面给出加权LeaderRank算法的一般表达形式：

(8)

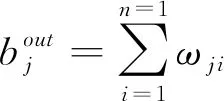
表1 偏差传递网络的网络特性及其计算方法

2.3 基于遍历回溯算法和ContributionIndex指标的关键误差溯源

零件加工过程中误差以加工特征为载体，在不同工序间进行传递。经2.2节中的关键节点识别方法确定了加工过程中的关键节点，为了使零件在加工过程中质量稳定，需要识别可能的误差源，从特定源头进行控制，能有效保证关键节点的加工质量，从而使整条生产线质量保持稳定。故需要对关键加工节点进行误差溯源。

根据特征节点重要度排序算法的结果，排名靠前的一定比例的节点为加工过程中的关键节点，即一旦出现质量偏差会对整个加工网络造成严重影响的系列节点。由于加权偏差传递网络是经过赋权的有向网络，为了便于计算机进行计算，转换成加权偏差传递二维矩阵。矩阵中的元素(i,j)表示误差从节点i传递到节点j。运用遍历回溯算法[21]对加权矩阵进行求解，得到所有可能的传播路径。本文算法的具体思想是确定关键加工特征后，在矩阵中找到指向该特征的节点作为第一步回溯的节点，再分别以第一步回溯结果中的节点进行回溯。经过一定步数后，能找到所有可能的关键传播路径。最后提出ContributionIndex指标的计算方法。该方法的基本思想是误差传播路径中的相关节点产生的误差都对目标节点造成了一定程度的影响，待测节点作用于目标节点的影响，可以用待测节点的延展强度乘以目标节点的误差吸收度占传播路径中所有节点的延展强度总和的比值来表示。即通过计算关键路径中待测节点的ContributionIndex指标，比较所有待测节点的ContributionIndex计算值，结果最大的待测节点则为误差源节点。具体方案如图4所示。为便于计算和考虑到溯源的精确性，遍历回溯算法的步长设定为3。具体步骤如下：

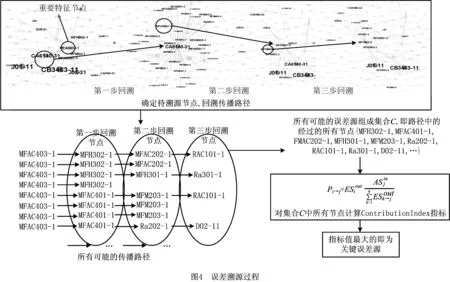
(1)以待溯源节点j为例，在加权误差传递矩阵中采用遍历回溯算法找出误差所有可能的传播路径后，将所有路径上的节点归入一个集合Ci→j，该集合Ci→j则为节点的可能误差源集，集合中的元素个数设为q个。

(2)对Ci→j集合中的每个节点元素进行计算。比较集合中的元素对节点j的贡献指标，确定可能性最大的误差源节点。计算公式如下：

(9)

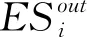
得到Ci→j中(Pi→j)max的节点则为最可能的误差源节点。同理可以得出其他待溯源节点的最大可能性误差源节点，从而识别整个加工网络上的关键误差源。对误差源进行重点监控，使得整个加工过程的质量得以保证。

3 实例分析

为了验证本文所提出的针对混合式多阶段加工系统的偏差传递建模以及误差溯源方法的有效性，选取内燃机主轴承盖的加工过程作为本文的研究对象。

图1上半部分呈现了主轴承盖加工过程的串并联多阶段的特征。由该主轴承盖的加工过程以及工艺要求可知该部件对加工有较高的精度要求，其加工精度直接影响主机的性能和寿命。因此，对主轴承盖的质量控制具有重要意义。

3.1 主轴承盖加工过程的偏差传递网络建模

内燃机主轴承盖的零件图如图5所示，由零件图可知该零件的加工工艺对外圆φ142k6通孔φ60H7的精度要求较高，对外圆面与通孔的同轴度要求较高，此外对M面、N面的位置，表面粗糙度都有较高的精度要求。

从主轴承盖加工工艺表(如表2)中得知N面为定位基准面，因此N为关键加工表面。根据加工工艺表中的信息，对主要的加工特征、加工要素等进行编码。为便于观察零件的定位基准面和方便行文，图6给出主轴承盖的装配图和部分加工特征编码，下文则以编码进行叙述。

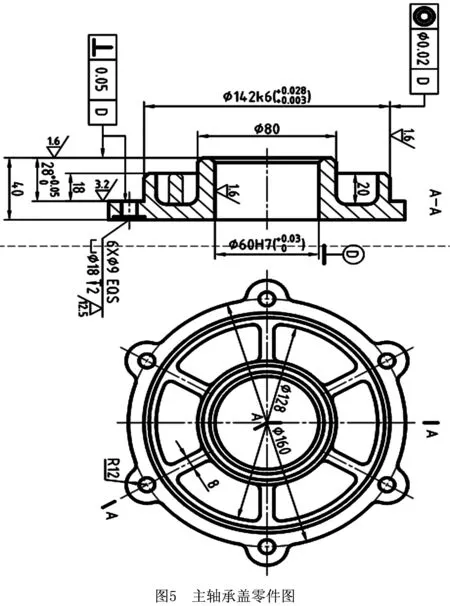
表2中的基准信息可以确定加工要素和加工特征之间的关系，以及连接不同加工特征的质量特征种类。

表2 主轴承盖零件加工工艺过程表

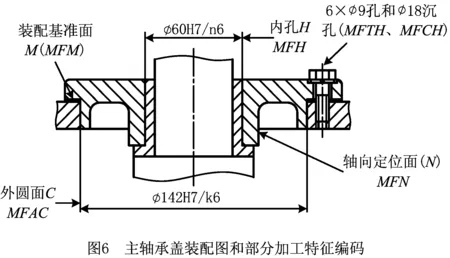
图2上半部分说明混合式多阶段加工中会出现多条加工路线同经一道工序的情况。因此，为了辨别关键加工特征所属的路线并进行溯源，下面对各加工路线中的各类节点进行编号。现以主轴承盖的多条加工路线为例，参照表2，将各加工设备、加工特征、基准面等进行编号，编号规则为：节点代号+工序号+(工步)+加工路线。如MFAC202-1表示第一条加工路线中第二道工序上的第一个工步粗车外圆；CA6140-21表示第一条加工路线中第二道工序上的普通车床。利用采集到的三条加工路线下的相关加工要素数据以及质量特征的误差值，结合2.1节中的自调节加权偏差网络建模方法，进行误差网络建模。最终构建的网络中共有86个节点，其中含有54个加工特征节点，32个加工要素节点。加权偏差传递网络如图7所示，图中的节点大小正比于节点度，因此图中较大的节点都具有较大的度，能直观地看出其中节点CA6140-31(普通车床)和节点J01-11(三爪自定心液压加紧卡盘)具有较大的节点度，即该类节点影响众多其他节点，在该网络中可能占主导地位。节点之间的连接方向为误差的传递方向，边的粗细表示误差传递的权重大小。

3.2 基于网络特性分析的关键加工特征识别

将主轴承盖的加权偏差传递网络转换成偏差传递矩阵后进行特性分析，包括节点度，度分布，簇系数，介数等。

根据表1的计算方法，可得到表3中网络特性计算结果。表3将加权偏差传递网络对应的偏差传递网络与同等规模的随机网络对比，发现相比于随机网络，偏差传递网络具有较大的簇系数和较小的平均路径长度，因此该网络具有一定的小世界效应。

表3 偏差传递网络与随机网络的特性对比

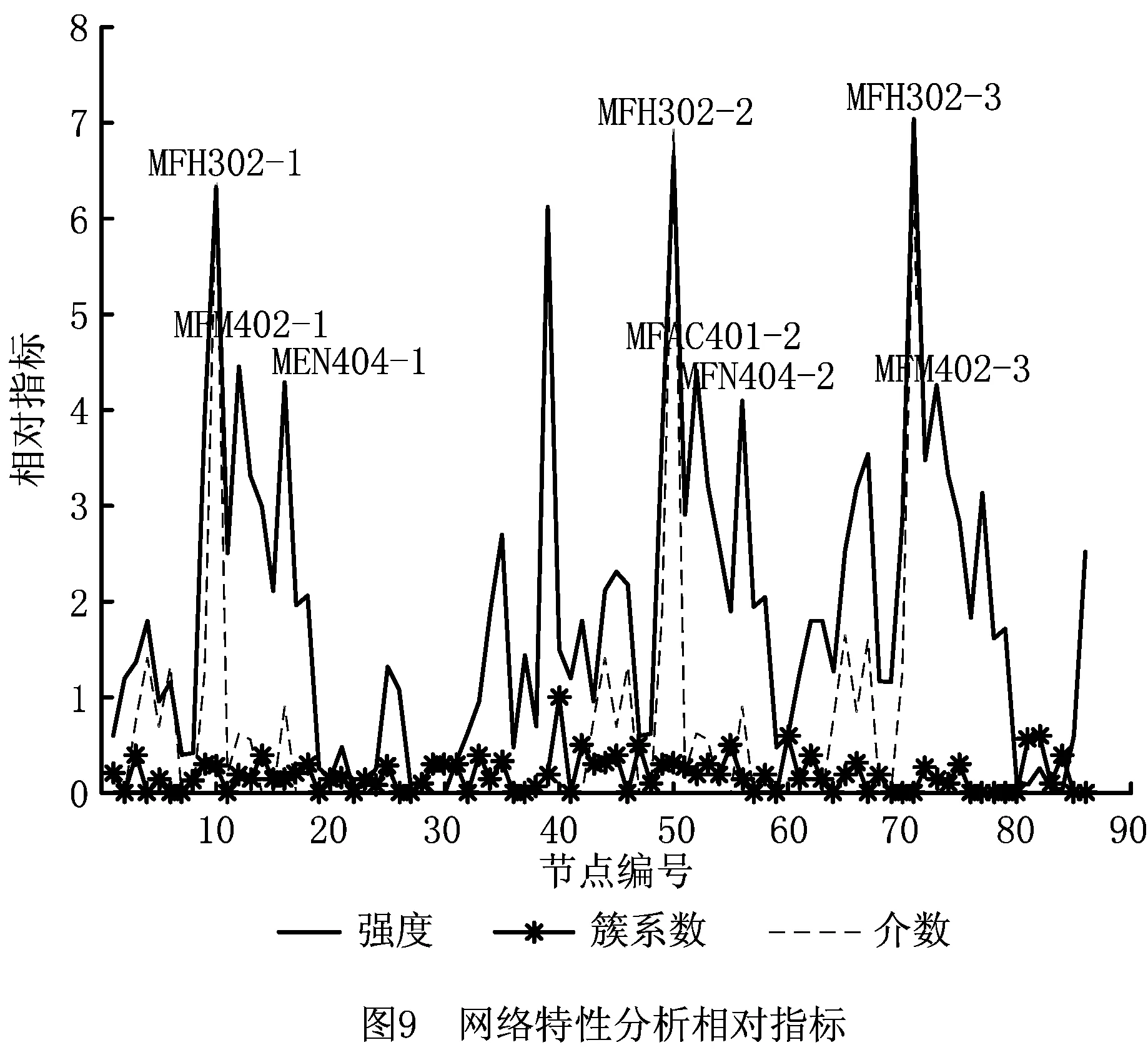
图8为网络的节点度和节点强度分布图，图中大多数节点的度聚集在一定的范围内，少数节点有较大的度，说明少数度大的节点在偏差网络中占据比较重要的地位。从图中可以得知J01-11(三爪自定心液压加紧卡盘)和CA6140-31(普通车床)虽然有较大的度，但是其节点强度并不算大。而MFH302(精车内孔)具有较大的节点强度，说明该加工特征在网络误差传递过程中可能起到重要作用。图9将加权偏差传递网络中的节点强度和其加工邻接矩阵的聚集系数以及介数加以比较。簇系数反映了网络的聚集程度，节点强度反映了网络节点的重要性，介数侧重反映了节点在网络传播中的重要程度。该网络中簇系数较大的节点普遍同时具有较大的介数，说明此类节点在网络中可能占有重要地位。

节点MFH302、MFM402以及节点MEN404同时具有较大的节点强度和介数，说明这些节点在网络中可能对误差的传播起关键作用，此外对于一些节点，如MFM402，虽然其节点度值不大但是具有较大的节点强度，说明此类节点工序质量波动明显，产生质量缺陷的概率较大。

为了进一步确定网络中的关键节点，经加权LeaderRank排序算法得到节点重要程度排序，结合表1中的计算方法，计算并绘制图10。从图10可知，加权LeaderRank排序算法对网络节点的重要性排序能够较好地拟合于加权簇系数排序结果和加权介数排序结果，并能够较好地对应于节点度大的节点。

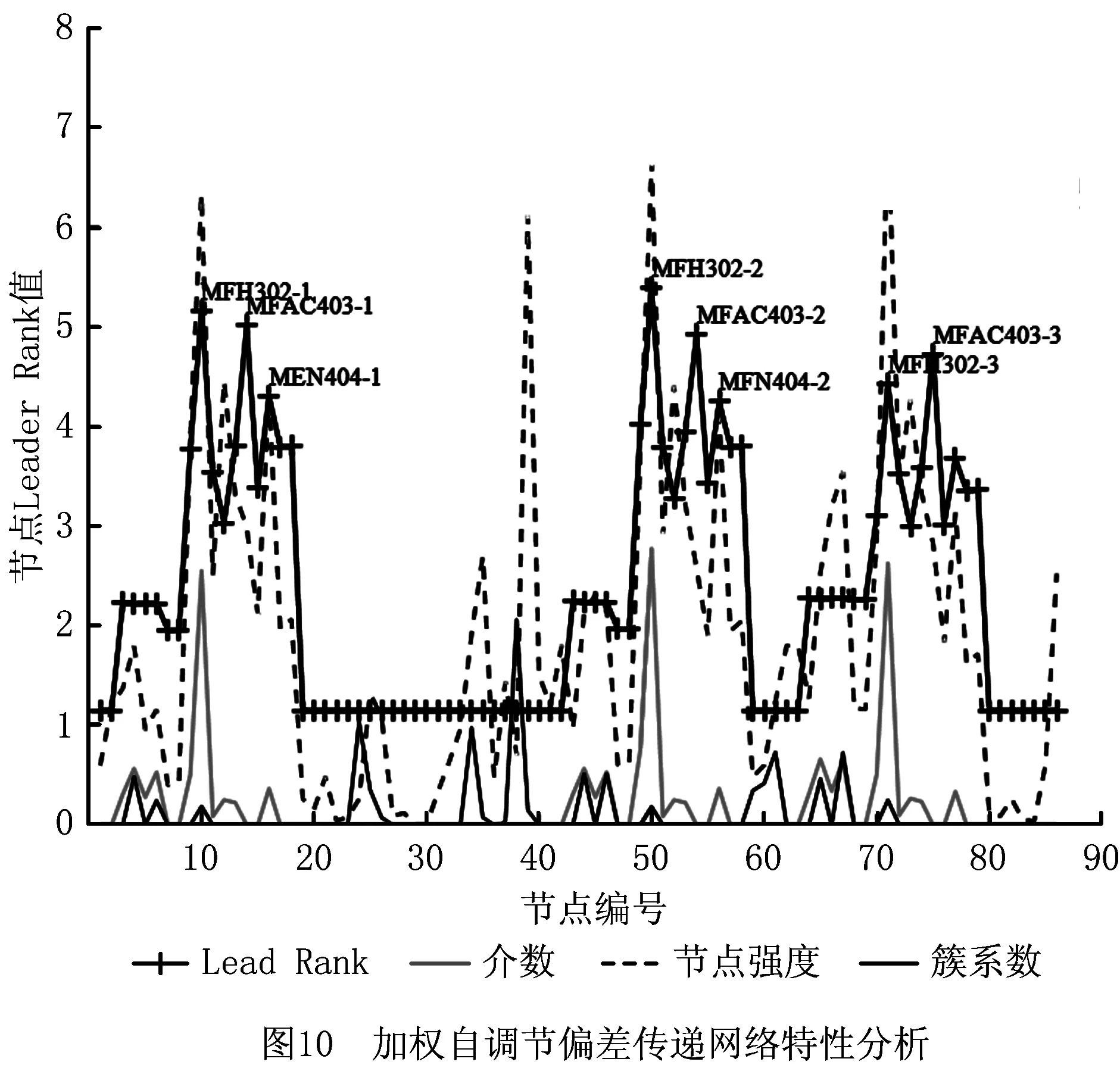
因此经过对主轴承盖的加权网络传播矩阵的特性分析，可以得出结论：在该混合式加工过程中节点MFH302(精车内孔)、MFAC403(精车外圆)、MEN404(精车N面)在整个网络中占有重要地位，为加工过程中的关键节点。

3.3 关键加工特性的误差溯源

在识别了加工过程中的关键节点，即确定了关键加工表面后，接下来对引起主轴承盖的关键加工质量缺陷的误差进行溯源，具体步骤如下：

步骤1确定关键加工表面。

由3.2节可得关键加工节点。上述关键节点包含3条加工路线上的3种加工特征，分别为精车内孔、精车外圆与精车N面。

步骤2回溯关键节点的误差传播路径。

以关键节点MFH302-1为例，在加权偏差传递矩阵中，采用遍历算法回溯到一定步长范围内所有可能的传播路径，算法简述如下。首先找到MFH302-1列中非零元素对应的横坐标即为第一步回溯的节点，再以第一步中找到的节点对应的列中非零元素对应的横坐标作为第二步回溯的节点，余同。最后将所有节点加入到集合Ci→MFH302-1作为误差源的待定节点，考虑到结果的精确性以及计算方便，本文选择的回溯步数定位3步。最终得到Ci→MFH302-1={RAC101-1，L101-1，MFH201-1，MFAC202-1，MFN203-1，MFH301-1，D01-11，D02-11，D03-11，D06-21，LO1，CB3463-11，CA6140-21，J01-11，J02-21}为对于节点MFH302-1的待定误差源集合。

步骤3待定误差源节点排序。

运用2.3节中的计算方法计算集合中节点的ContributionIndex指标。计算结果如表4所示。即由各个误差待定节点的贡献度指标可知，对节点MFH302-1贡献度最大的节点为CA6140-21，则可以确定MFH302-1节点的误差源节点为CA6140-21(普通车床)。同理，对其他关键节点进行误差传播路径溯源以及对待定误差源节点的排序结果整理如表5所示。

由此可知，精车内孔的误差源主要为普通车床CA6140-21和三爪自定心液压夹紧卡盘J01-12，精车外圆的误差源为精车外圆液性塑料夹具J03-31，精车N面的误差源主要为外圆端面精车刀D07-31。因此在生产过程中需要着重对以上加工要素进行严格控制。

表4 对应节点MFH302-1的待定误差节点误差贡献度

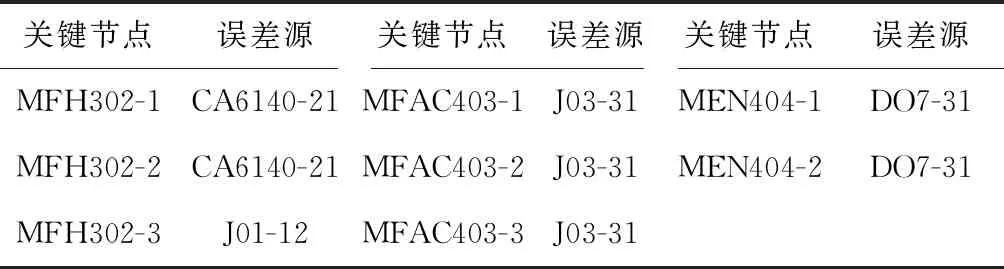
表5 关键节点及其对应的误差源节点

4 结束语

本文提出了基于复杂网络的混合式多阶段加工偏差传递建模与误差溯源方法，并通过对具有代表性的主轴承盖的实例分析，验证了该方法的有效性。提出的网络建模以及误差溯源方法也为混合式多工序制造过程的质量控制提供了新思路。在实际生产加工过程中，误差的种类多样，大小难以确定，此外对于过于复杂的加工过程，整个加工网络过于庞大，而工序内的网络连接相对工序间要紧密得多，因此对庞大网络进行模块划分，并在区分的不同模块中进行误差诊断和溯源，将有效提高质量控制的效率，这也将成为后续研究的重点。