高强度钨板矫直过程中辊间张力的影响分析

四川建筑职业技术学院 机电与信息工程系 四川德阳 618000

1 分析背景

在目前所有已知的天然金属中,钨具有熔点高、热膨胀系数小、高温环境下化学性能稳定、对辐射有较高吸收能力、合金易于加工等特点,被广泛应用于超高温、高真空环境中,如玻璃密封、高温炉结构件、辐射吸收材料,以及其它军工、航空、航海领域[1-3]。高强度钨板作为钨的一种重要成形件,其平直度等质量指标直接由辊式矫直过程的矫直精度决定[4-6]。高强度钨板在辊式矫直后,往往上下表面会出现划痕。当钨板太薄时,矫直过程中会出现轻微堆叠现象,矫直辊传动过程中还会出现负扭矩。上述现象已被部分专家学者所了解,但尚未进行系统和深入研究。文献[7]认为,板材在矫直过程中,因为压下量的变化才会出现板材堆叠和矫直辊负扭矩等现象。实际上,高强度钨板的整个辊式矫直过程都属于非线性连续弹塑性弯曲过程,且弯曲曲率不相同,这会导致高强度钨板中性层位置的速度不同,从而形成张力,产生上述现象[8-10]。为深入了解并改善以上现象,需要建立高强度钨板辊式矫直的辊间张力理论算法,并通过试验对算法进行验证,从而为进一步增强高强度钨板的矫直质量提供依据。

2 高强度钨板矫直辊间张力模型

在传统的矫直研究领域,通常将板材矫直过程中出现的负扭矩等现象统称为辊间张力。在多辊传动的设备和仪器中,辊间张力广泛存在。在力学研究中,通常将产生拉应力的张力视为正,将产生压应力的张力视为负。高强度钨板在整个辊式矫直的连续弯曲过程中,具体受力如图1所示。高强度钨板在连续交错布置的矫直辊之间发生连续弯曲变形,在这一过程中,主要受力包括钨板与矫直辊垂直接触的压力Pi、整个矫直过程的驱动扭矩Ti。而多辊传动形成的辊间张力fi则是整个矫直系统的内力,其具体分布位置在高强度钨板与矫直辊的相邻接触点之间。高强度钨板的矫直过程总体上有三个阶段,即先期咬入、中间阶段的稳定矫直和出口处的甩尾。其中,稳定矫直阶段通常指高强度钨板头部经过全部矫直辊及尾部驶离入口矫直辊。在这一理想状态的稳定矫直阶段,假设高强度钨板为理想板材,则上述三个参数矫直辊垂直接触压力Pi、驱动扭矩Ti、矫直辊间张力fi在固定的时间点都是确定的。

传统矫直过程如图2所示,前后相邻的三个矫直辊之间会形成一个反弯单元。可以将高强度钨板的矫直视为高强度钨板连续经过N个反弯单元,板材在每个反弯单元的受力情况基本相同,所以选取其中一个反弯单元进行分析。在一个忽略其它影响的矫直反弯单元中,矫直总外力做功基本全部转化为高强度钨板的变形能。在忽略其它影响的矫直反弯单元i上,假设高强度钨板前后两端所承受的张力分别为fi和fi+1,则该单元上矫直总外力,即驱动扭矩Ti所产生的功等于高强度钨板的变形能Usi消耗,有平衡方程:

Til/R+fi+1l-fil=lUsi/R

(1)

式中:R为矫直辊半径;l为高强度钨板在一个反弯单元中的整段长度。

图1 高强度钨板矫直受力

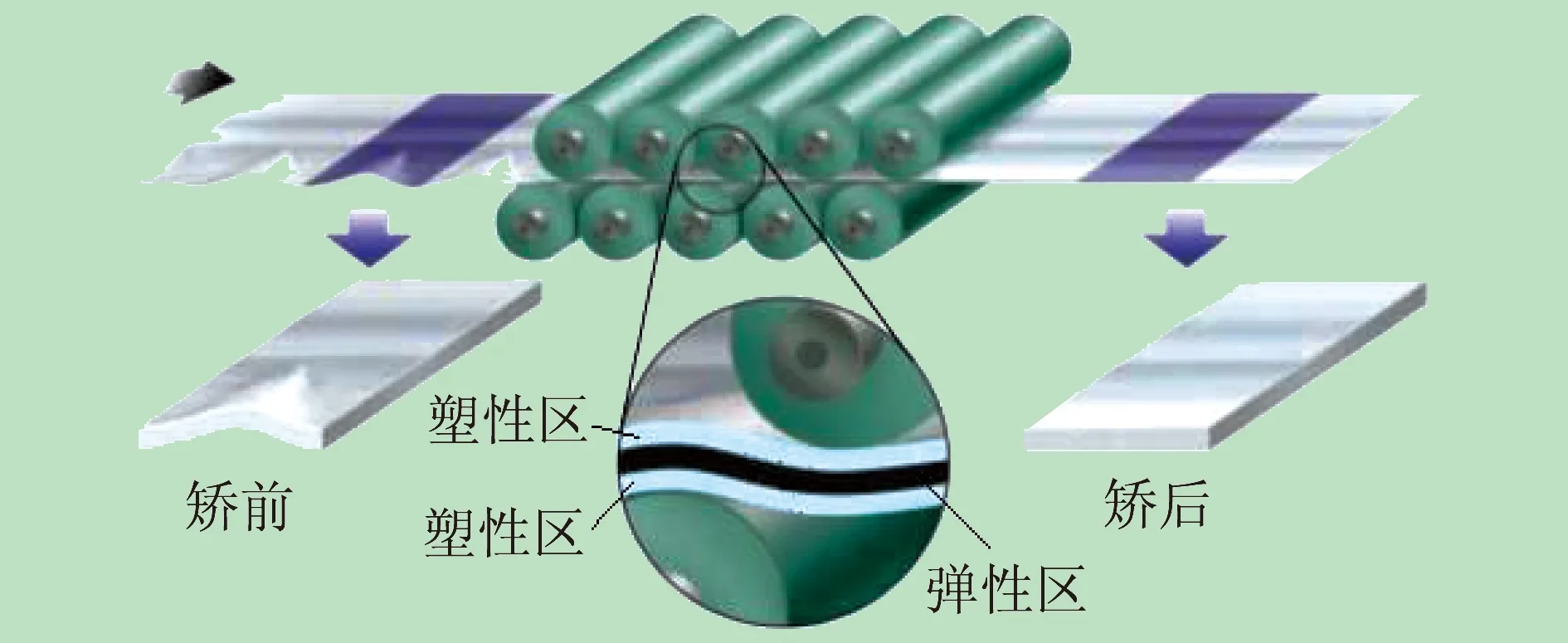
图2 传统矫直过程

高强度钨板在一个反弯单元中的变形能Usi,其实质是高强度钨板发生塑性变形所消耗的能量。假设在一个反弯单元中,高强度钨板只发生弹性变形,那么其变形能Usi的值为零。如果高强度钨板在一个反弯单元中发生塑性弯曲,那么其总变形能由两部分组成:一部分是塑性弯曲前的弹性弯曲能,最终会在卸载后释放;另一部分是为产生塑性弯曲而消耗的永久变形能。

式(1)可简化为:

fi+1-fi=Usi/R-Ti/R

(2)

在高强度钨板的整个矫直过程中,每个反弯单元都可以根据上述方程建立等式。假设矫直机的矫直辊辊数为J,那么在整个矫直过程中,就会形成J+1个辊间张力f,进而可以有J个等式。与此同时,又因为矫直的进出口处没有约束为自由段,有f1=fJ+1=0,所以如果能测得矫直过程中的驱动扭矩,那么就可以计算出矫直过程中的所有辊间张力。此外,由式(2)可知,驱动扭矩、变形能与辊间张力之间一直保持着动态平衡。

在测量过程中,实测驱动扭矩理论上还包含了正常摩擦的能量消耗,则实测驱动扭矩Ni为:

Ni=Tsi+Tki+Tmi

(3)

式中:Tsi为矫直计算的理论驱动扭矩;Tki为高强度钨板与矫直辊之间因摩擦所产生的扭矩;Tmi为矫直辊与滚动轴承之间因摩擦所产生的扭矩。

Tki、Tmi的计算可参考文献[7]。

3 高强度钨板矫直辊间张力计算

在高强度钨板的整个矫直过程中,有:

Vmi+1-Vmi+Vμi+1-Vμi=0

(4)

式中:Vmi+1、Vmi分别为高强度钨板与第i号和第i+1号矫直辊直接接触处的线速度;Vμi+1、Vμi分别为高强度钨板与第i号和第i+1号矫直辊之间的相对滑移速度。

假设高强度钨板与第i号和第i+1号矫直辊之间未能形成相对滑移,则式(4)可以简化为:

Vmi+1-Vmi=0

(5)

在高强度钨板的矫直过程中,第i号矫直辊处还会产生蠕变。高强度钨板在第i号矫直辊处的蠕变量ξi为:

(6)

式中:VRi为第i号矫直辊最外表面的平均线速度;VSi为高强度钨板与第i号矫直辊直接接触处的速度。

对于第i号矫直辊,还有:

(7)

式中:εi为高强度钨板与第i号矫直辊接触处的表面应变。

将式(6)和式(7)代入式(4),可得:

(8)

ξi的能量方程为:

(9)

(10)

Fi=Ti/R+fi-fi-1

(11)

式中:μ为高强度钨板与矫直辊之间的摩擦因数;ai为高强度钨板与第i号矫直辊之间的半接触宽度;Fi为高强度钨板与第i号矫直辊之间形成的水平力;Pi为高强度钨板与第i号矫直辊之间形成的垂直接触压力;ν1、ν2分别为高强度钨板和矫直辊的泊松比;E1、E2分别为高强度钨板和矫直辊的弹性模量;b为高强度钨板的宽度;ρ为高强度钨板的反弯曲率半径。

联合式(8)～式(11),即可求出高强度钨板的辊间张力。

4 试验分析

所选用的试验设备为全液压压下辊式矫直设备,如图3所示。矫直设备的总矫直辊数为11条,从入口到出口,矫直辊依次按顺序编号为1号至11号。全部矫直辊直径为90 mm,入口处和出口处为了方便高强度钨板的咬入、甩出,矫直辊辊距为120 mm,其余处矫直辊辊距为100 mm。所能承受的矫直力上限为2 000 kN,可矫高强度钨板的厚度范围为2～12 mm,可矫高强度钨板的宽度上限为1 000 mm。矫直驱动扭矩可通过连接矫直辊的万向接轴上的弹性元件来采集。

图3 全液压压下辊式矫直设备

试验采用W1高强度钨板,主要参数见表1。

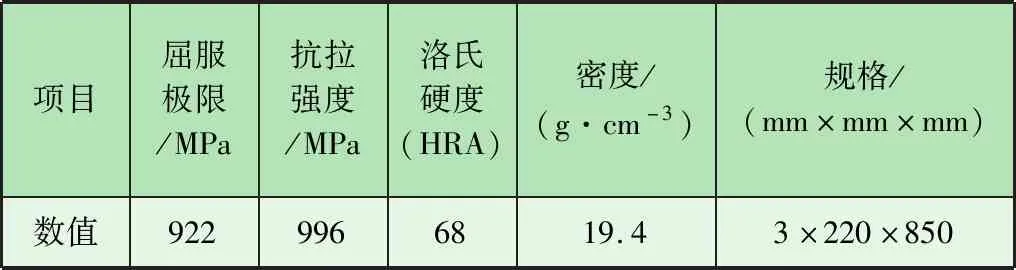
表1 高强度钨板参数

假设在矫直过程中,高强度钨板中性层处的前行速度为V,矫直辊外表面的平均线速度为Vg,当矫直辊缝等于钨板板厚,即无压弯量时,Vg=V。当矫直辊缝隙小于钨板板厚,即有压弯量时,高强度度钨板就会在矫直过程中发生弹塑性弯曲变形。与此同时,高强度钨板与矫直辊的接触表面会形成纵向收缩,从而形成弯曲应变。假设在第i号矫直辊处高强度钨板形成的弯曲应变量为εi,则该处的表面线速度为εiV。在一个连续矫直弯曲过程中,由于各处的压弯量可能不同,因此高强度钨板在各矫直辊处的弯曲应变量εi也会不同,进而导致高强度钨板与矫直辊接触的表面速度V和矫直辊外表面的平均线速度Vg也会不同。如果矫直过程采用最常用的倾斜压下矫直方案,并忽略辊系边部的影响,那么11条矫直辊处的弯曲应变量有关系ε1<ε2<ε3<ε4>ε5>…>ε11,由此可知4号矫直辊处的弯曲应变量最大。假设矫直辊与高强度钨板在接触位置无相对滑移,则在4号矫直辊位置高强度钨板中性层处前进速度最快,并向两端依次减慢。实际上,各矫直辊处的速度差是引发张力产生的主要原因。

通过试验,高强度钨板在稳定矫直阶段的实际驱动扭矩与理论扭矩之间的对比如图4所示。由图4可知,在稳定矫直阶段以4号矫直辊为分界点,之前的矫直辊,驱动扭矩逐渐增大,之后的则逐渐减小。3号和4号矫直辊位置处的驱动扭矩最大,所承担的弯曲变形驱动能也最大。其中,4号矫直辊位置处的实测驱动扭矩为150 N·m,几乎是理论扭矩的3倍。另外,1号和8号矫直辊位置处出现了负扭矩,5号至11号矫直辊位置处的实测驱动扭矩都比理论扭矩小,从而与之前的大驱动扭矩配合,形成产生高强度钨板弯曲变形的推动功。由图3可知,实测驱动扭矩与理论计算驱动扭矩差别较大,原因是理论驱动扭矩的计算模型主要依据单个反弯单元的塑性变形,忽略了高强度钨板在矫直过程中受到的辊间张力影响,由此产生了很大的偏差。

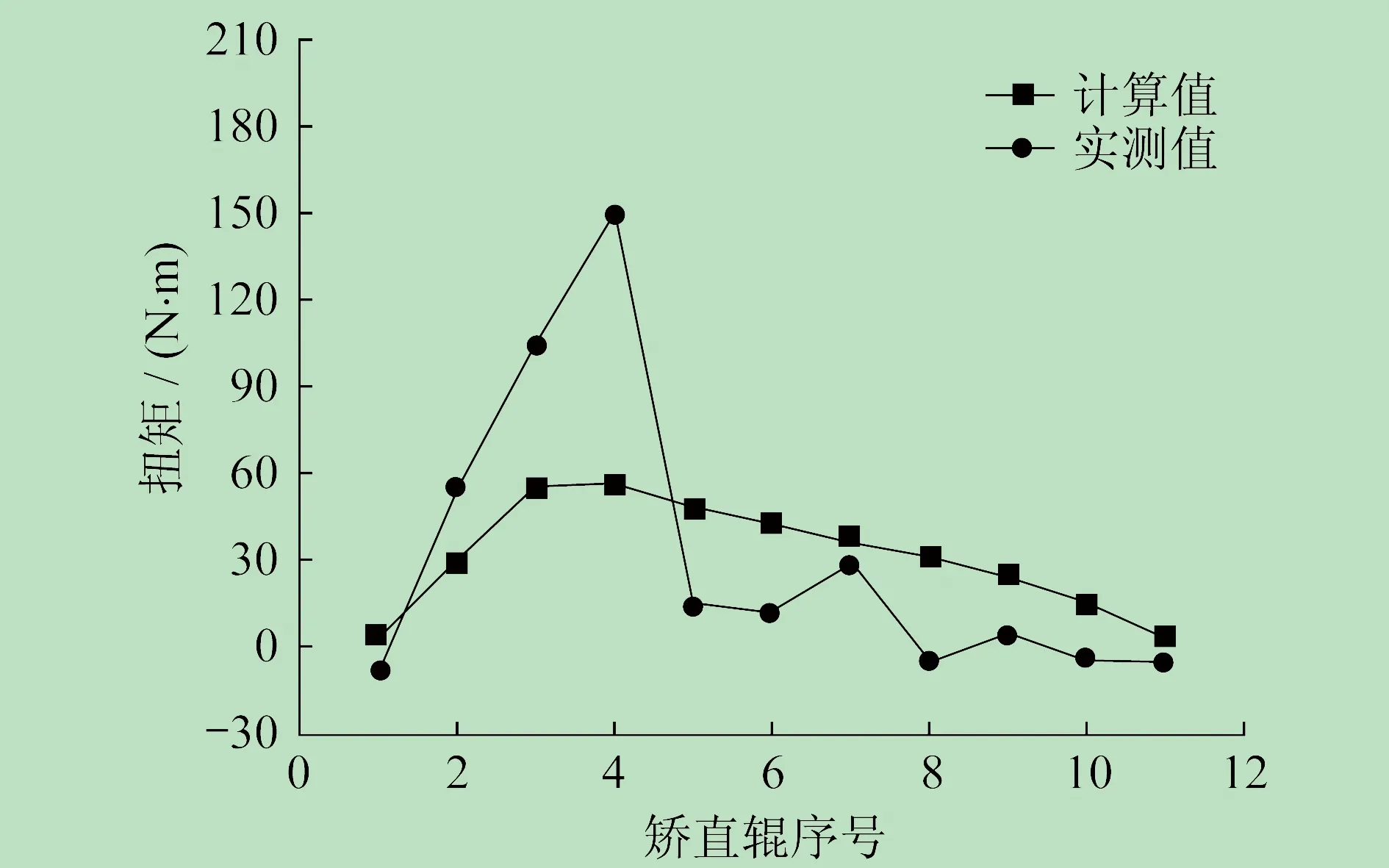
图4 矫直驱动扭矩对比

根据上述计算模型计算得到的各矫直辊处参数见表2。辊间张力fi计算结果见表3,试验测得的实际辊间张力fi如图5所示,可见计算所得的辊间张力变化规律与试验基本相同。进出口处无约束,f1=f12=0。第一个反弯单元为咬入,f2为拉力。其余各处的辊间张力都是压力,其中辊间张力的最大值在4号和5号矫直辊之间,为-3 503 N。在本次矫直试验中,各位置处的辊间张力分布趋势与相对应位置的高强度钨板中性层速度分布趋势基本相同,即4号矫直辊位置处最大,向两侧逐渐减小。

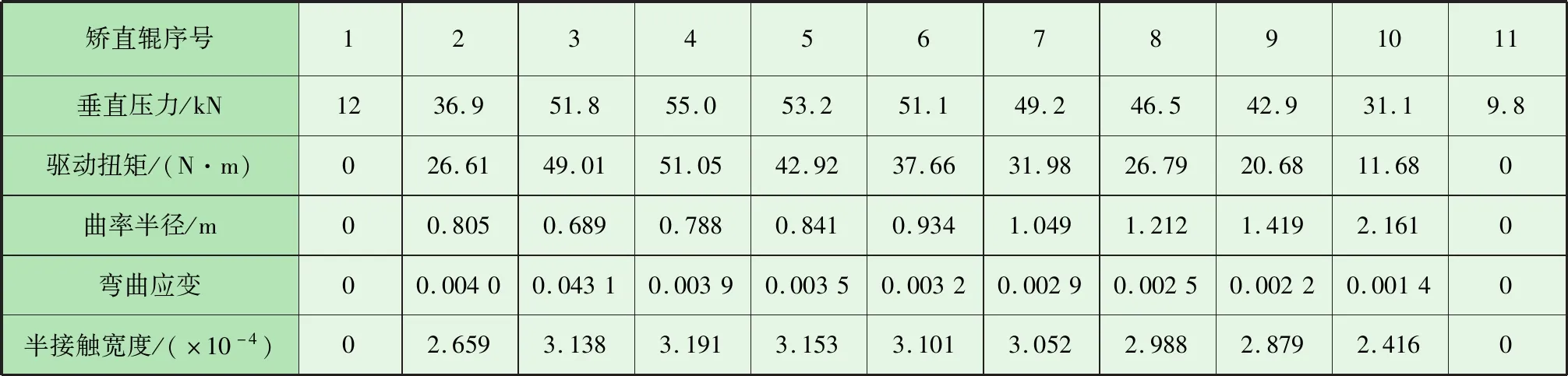
表2 各矫直辊处计算参数

表3 辊间张力计算结果

通过试验可知,由于矫直过程中存在辊间张力,会对高强度钨板产生附加应力σi,其分布如图6所示。辊间张力越大,所产生的附加应力也越大。其中,4号和5号矫直辊之间的附加应力最大,为-2.4 MPa,接近高强度钨板屈服强度的1%。该附加应力会引起矫直过程中高强度钨板中性层偏移,进而对内弯矩的计算产生影响。

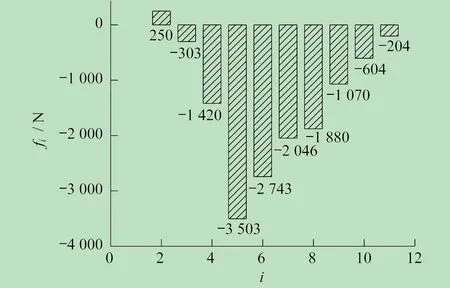
图5 实测辊间张力分布

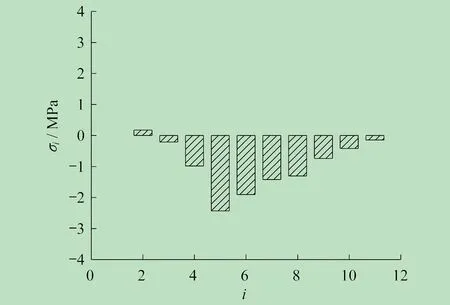
图6 附加应力分布

矫直过程中,驱动扭矩所需的能量是通过矫直辊与高强度钨板之间的摩擦来实现传递的,摩擦因数为0.05～0.10。矫直辊各位置处和高强度钨板之间的传动作用力与摩擦力分布如图7所示。由图7可知,如果无法确定具体的摩擦因数,那么就无法判断高强度钨板在矫直过程中是否打滑。例如,当摩擦因数为0.06时,4号矫直辊处与高强度钨板之间的传动力已大于摩擦力,将出现打滑。当然,也只有4号矫直辊位置处最容易出现打滑,因此对辊间张力的影响是局部的。

5 结束语

高强度钨板在矫直过程中普遍存在辊间张力,如果能确定驱动扭矩,那么辊间张力可以通过模型计算得到。在高强度钨板的矫直过程中,由于辊间张力的影响,实际驱动扭矩的分布与传统理论计算结果之间有较大偏差。其中,3号和4号矫直辊承担了绝大部分驱动扭矩。在本次矫直试验中,辊间张力fi在自由端有f1=f12=0,第一个反弯单元因为咬入使f2为拉力,其余各位置处的辊间张力均为压力。其中,辊间张力的最大值在4号和5号矫直辊之间,为-3 503 N。矫直过程中,驱动扭矩是使高强度钨板产生反弯变形的能量来源,且能量是通过摩擦来实现传递的。根据不同大小的摩擦力,4号矫直辊位置处最容易出现打滑,因此对辊间张力会产生局部影响。

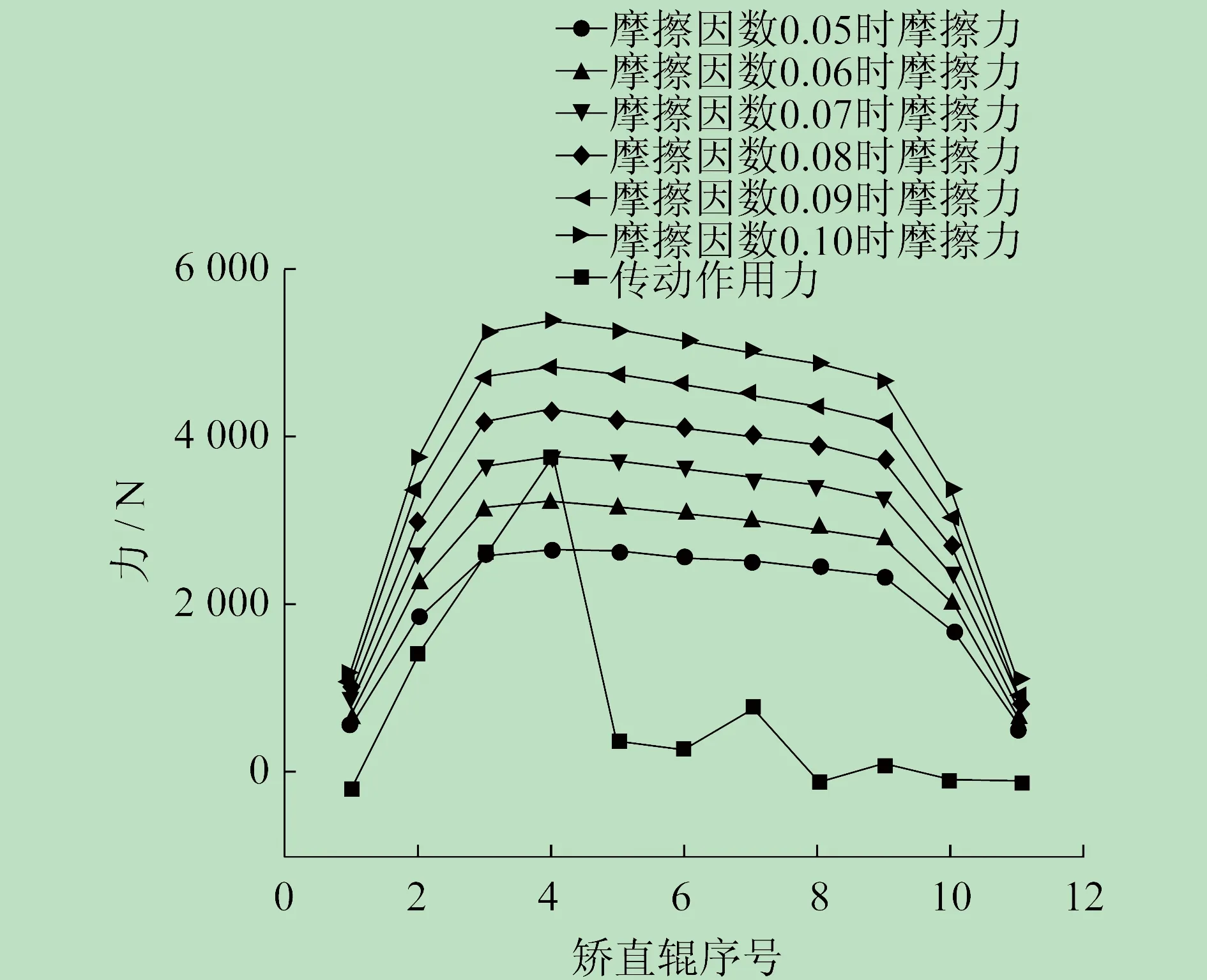
图7 传动作用力与摩擦力分布