自适应虚拟阵列在深空探测中的应用方法

李 渝，张鑫诚，高 峰，王伟伟，段崇棣*

(1.中国空间技术研究院西安分院，西安 710000;2.西安应用光学研究所，西安 710065;3.中国空间技术研究院，北京 100094)

0 引言

共形天线[1-2]的阵列结构可根据任务需求安装在军用飞艇、航天飞机、卫星甚至导弹等目标表面，相比传统的均匀阵列结构天线，其灵活的阵元排布结构可大幅降低平台对气动性能的要求。同时共形天线的孔径一般较大，可实现较高的测向精度，因此共形阵列在未来的深空探测领域具有显著的优势。然而，探测一般对信号处理的实时性要求较高，共形阵列的特殊结构一般不具有Vander monde结构，快速信源波达角(Direction of Arrival，DOA)[3-4]超分辨估计方法无法适用，严重限制了共形天线的应用。

为了实现任意结构共形天线的快速DOA估计，目前国内外学者提出了许多解决手段。 Fabio B利用流形分离技术[5]将共形阵列天线导向矢量表示为均匀线性阵列导向矢量与采样矩阵的乘积形式，利用傅里叶基实现了快速DOA估计。文献[6]将流行分离技术应用于3维阵列DOA估计中，以计算复杂度为代价实现了二维平面角的高精度估计。考虑到圆形阵列360°的探测能力，Cook[7]等人将虚拟内插应用于圆形共形天线的多目标探测中，通过控制扇形区域外信号的响应，有效降低了扇形区域内来波方向的探测误差。文献[8]提出了一种基于酉矩阵求根的L型阵列天线测频和测角实现方案，相比多重信号分类算法，可同时兼顾DOA搜索精度的鲁棒性以及运算复杂度。Hassanien[9]提出了一种基于FFT的快速DOA估计方法，该方法利用迭代插值运算有效剔除了多个信号间空域旁瓣的相互干扰，DOA估计精度优于子空间类算法。Chen Hao[10]等人通过对虚拟内插变换后的虚拟协方差矩阵进行SVD特征分解，利用信号子空间与噪声子空间的正交性得到了目标空间谱的高精度估计。上述方法一定程度上提升了共形天线快速DOA估计性能，但难以同时兼顾共形天线任意构型、探测精度和计算复杂度等指标。

考虑到虚拟阵列探测性能主要受角分辨力、转换误差和实时性等因素的影响，其中虚拟孔径越大，角分辨率越高；虚拟阵列与真实阵列导向矢量差异越小，转换误差越小；虚拟阵元数目越小(相同阵列结构)，信号处理复杂度越低。本文提出了一种自适应虚拟阵列在深空探测中的应用方法，该方法利用虚拟阵列天线的结构变换灵活性，采用最优自适应变换策略实现了多角度无孔径损失的快速DOA估计，通过多种虚拟阵列构型的DOA估计均方根误差、导向矢量转换误差以及实时处理能力的对比，得到了自适应虚拟阵列的最优构型。该方法不需要复杂的硬件成本为代价，适用于工程中先验信息不足条件下的稳健DOA估计。

1 虚拟阵列变换方法

1.1 虚拟内插变换原理

共形阵天线阵元位置分布不同于均匀线性阵列，即不满足Vander monde结构，因此实现角度估计复杂度较高，因此工程应用受到制约。虚拟内插变换方法通过在某个限定的角度区间寻找变换矩阵，可实现真实阵元与虚拟阵元导向矢量的转化，下面介绍虚拟内插变换的原理。

Bi=(AAH)-1ABH

(1)

变换后的协方差矩阵可表示如下

(2)

其中S表示目标信号矢量，σ2为噪声方差。

(3)

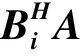
1.2 虚拟阵列的内插方式

考虑到空气动力学对卫星平台的影响，共形天线结构在卫星表层的结构一般具有对称性，本文以圆形二维共形阵为例，介绍几种虚拟阵列的内插方式。

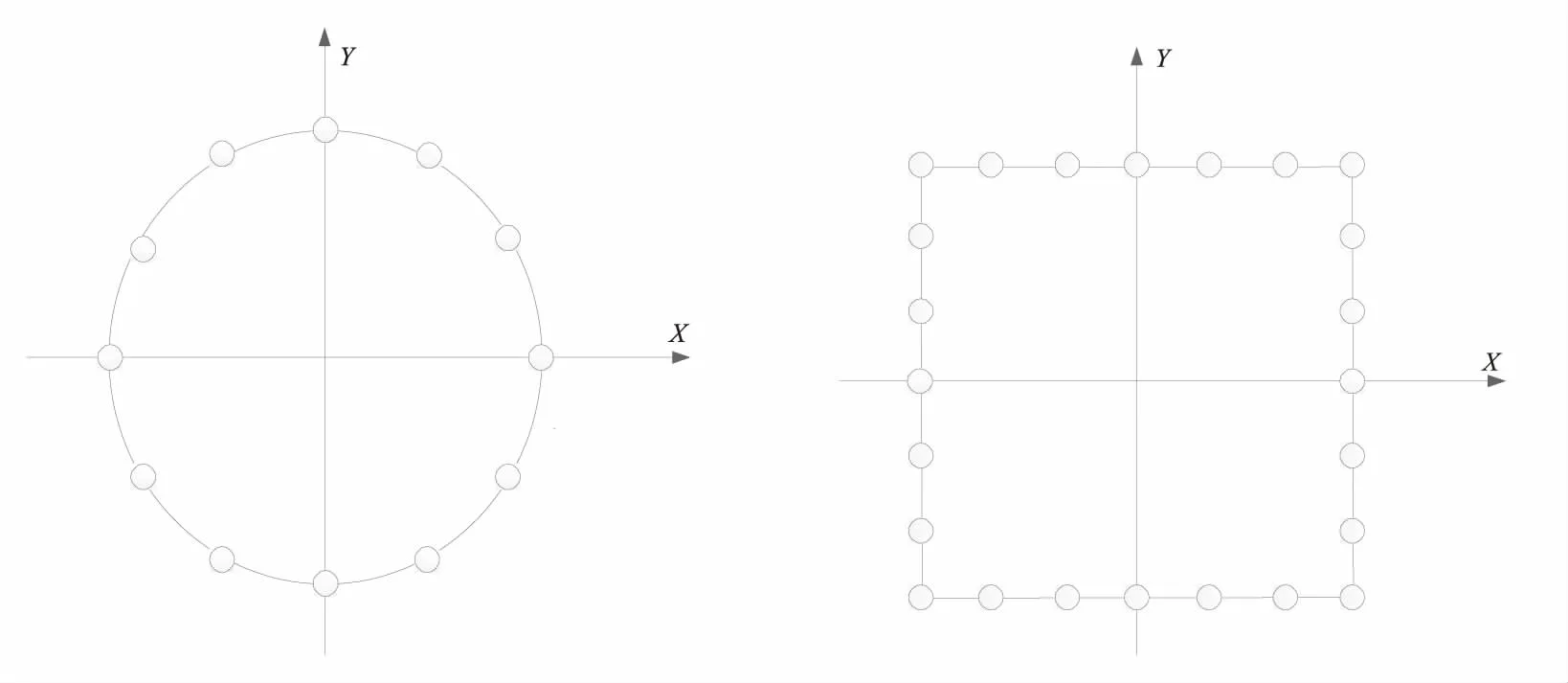
(a) 原阵列 (b) 虚拟矩形阵列

(c) 虚拟L形阵列 (d) 虚拟十字阵列

图1(a)为由12阵元等间隔排布组成的真实阵列示意图，其中真实圆阵列半径r=3d，为考虑到真实阵列向虚拟阵列转换时，要保证两者在不同方位角和俯仰角导向矢量的相似性，才能最大程度地降低转换误差，因此本文选择矩形、L形以及十字形作为虚拟阵列的变换结构。图1(b)、图1(c)和图1(d)分别为虚拟内插变换后得到的虚拟矩形阵列、虚拟L形阵列、虚拟十字阵列示意图，其中虚拟阵元间距为d。

2 自适应虚拟阵列变换方法

2.1 自适应虚拟阵列内插方式

图2(a)给出了来波方向与阵列几何结构示意图，其中 代表方位角， 代表俯仰角。由第二节虚拟内插方式可知，虚拟阵列虽然满足等间隔均匀排布，但在不同方位角和俯仰角对应的探测区域，其二维孔径是不断变化的，导致某些探测方向不可避免的存在孔径损失。

针对上述问题，本节给出一种自适应虚拟阵列变换方法，如图2(b)所示，可以看出，虚拟十字阵列的一条轴向指向探测区域，其虚拟阵元位置随探测区域的方向不断变换，因此这种自适应虚拟内插方式具有稳健的角分辨能力。表1列出了不同阵列结构对应的二维最小孔径，显然，只有自适应虚拟阵列和矩形阵列与原共型阵的二维孔径相同，其他虚拟阵列的最小孔径明显小于原阵列。另外，俯仰向虚拟孔径小于方位向虚拟孔径，这主要由于原阵列是二维平面阵，俯仰向孔径受来波俯仰角的约束。如果要提升俯仰方向的孔径长度，只需将原阵列变换为三维立体阵列即可，其他变换策略与本文方法类似。

(a)来波方向示意图

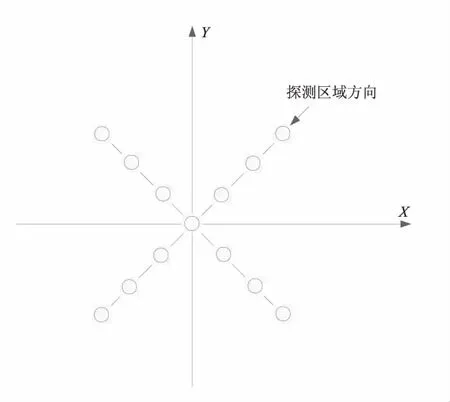
(b)自适应虚拟内插方式

表1 二维最小孔径

2.2 转换误差分析

考虑到虚拟阵列导向矢量与真实阵列导向矢量的差异，虚拟阵列的探测性能不仅受虚拟孔径的影响，还受到导向矢量转换误差的影响。转换误差的定义如下

式中 ‖‖F表示F范数运算，若真实阵列与虚拟阵列在探测角度(θ,φ)导向矢量越相似，转换误差越小。图3显示了几种典型的虚拟内插方式在不同探测角度对应的转换误差大小，可以看出，十字阵在整个角度域的转换误差最小，这也是自适应虚拟阵列选取十字阵结构的原因之一。由于平面阵在俯仰向缺少自由度，随着俯仰角的增加，三种虚拟阵列的转换误差均大幅上升。

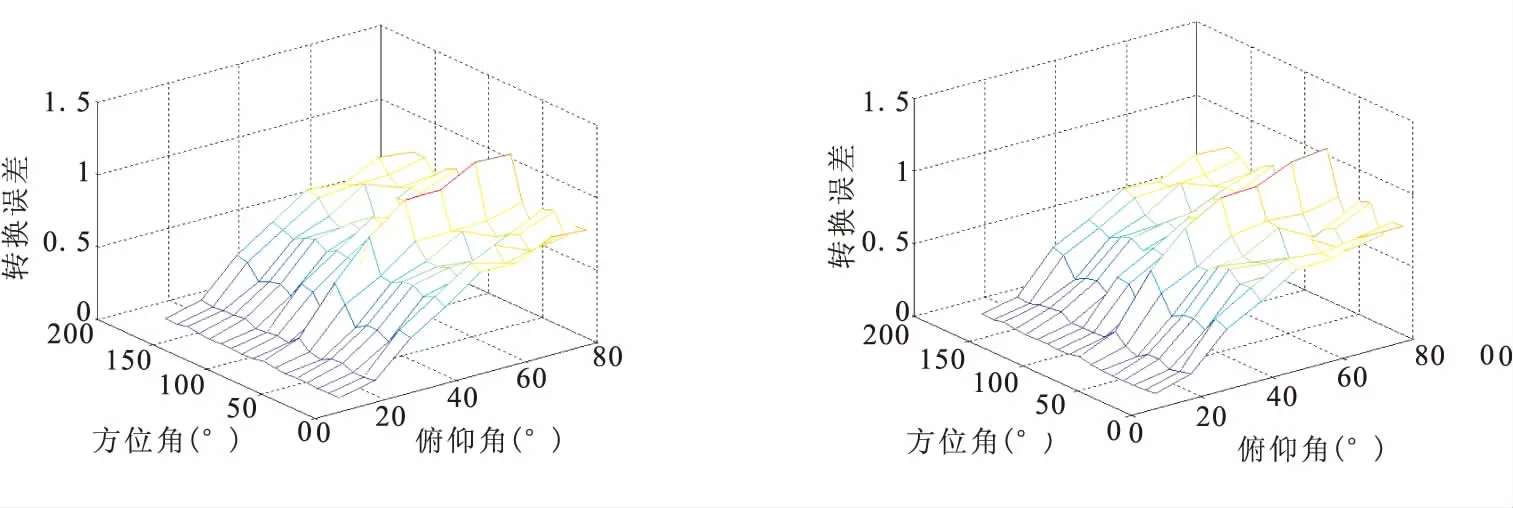
(a) 矩形阵列转换误差 (b) L形阵列转换误差

(c)十字阵列转换误差

2.3 计算复杂度分析

假设圆形阵列阵元数为N，谱峰搜索点数为Num，虚拟阵列线阵阵元总数为M，为了方便计算量的对比，令探测区域角度域个数为Num。对于圆形阵列，由于导向矢量不具有Vander monde结构，不能使用快速DOA估计算法，这里以MUSIC算法为例分析圆形阵列DOA算法计算复杂度[10]信号与噪声子空间分解对应计算复杂度为O[15(N-1)3]，峰值点搜索对应计算复杂度O[Num(N2+N)]。

对于虚拟阵列，真实阵列到虚拟均匀线阵转换计算复杂度为O[NumN3+NumM3]，这一步计算复杂度较高，但是考虑到虚拟阵列构型已知，转换矩阵可以进行离线计算，并不影响探测算法的实时处理能力。由于虚拟阵列的导向矢量具有Vander monde结构，因此快速DOA估计算法适用，以Root-MUSIC算法为例，虚拟均匀线阵DOA估计运算复杂度为O[120(M-1)3]，显然，120(M-1)3≪[15(N-1)3+Num(N2+N)]，虚拟阵列计算复杂度明显低于圆形阵列的计算复杂度。

根据上述计算复杂度分析方法，表2列出了不同阵列结构进行DOA估计需要的计算复杂度，几种虚拟阵列中虚拟矩形阵列计算复杂度最高，其他几种虚拟阵列计算复杂度相同，因此自适应虚拟阵列不采用矩形阵列结构。

表 2 计算复杂度

虚拟阵列的探测性能主要受虚拟孔径和转换误差的影响，根据本节的分析，综合考虑几种虚拟阵列的二维虚拟孔径、转换误差和DOA估计运算复杂度，本文选取虚拟十字阵列作为自适应虚拟阵列结构，其结构示意图如图2(b)所示。

3 仿真结果

本节通过对真实阵列与虚拟阵列在DOA估计性能和抗干扰能力[11]的差异进行仿真对比，对上述理论分析的正确性做进一步验证。

DOA估计性能：

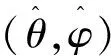
(5)

式中 函数length表示求矢量长度运算，Vec和Vec0分别代表真实信号三维角度矢量和DOA估计三维角度矢量，具体表达式如下

(6)

Vec=[sin(φ)*cos(θ),sin(φ)*sin(θ),cos(φ)]

(7)

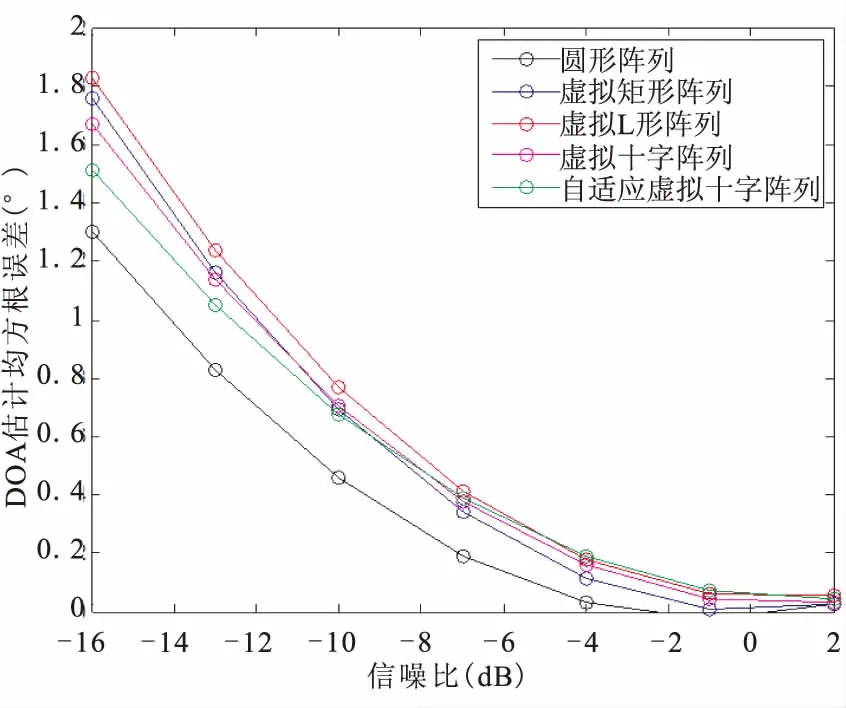
图4 DOA估计均方根误差与信噪比的关系

图4为不同虚拟阵列DOA估计均方根误差随信噪比的变化曲线，仿真中蒙特卡洛次数设为1000，来波信号为S波段，波长为0.085，一个相干处理间隔(Coherent process interval, CPI)共包含1024个脉冲，信噪比(Signal to Noise Ratio, SNR)区间设为-16dB～2dB。由于自适应虚拟阵列与圆形阵列的虚拟孔径和转换误差最接近，其DOA估计性能在几种虚拟阵列中是最优的，这与理论分析相一致。随着信噪比的提升，不同虚拟阵列DOA估计性能逐渐趋于一致。

抗干扰性能：

假设来波方向(φ，θ)=(90°,30°),干扰方向(φj，θj)=(75°,50°)，信噪比区间设为-20dB～20dB，干信比(Interference to Signal Ratio, ISR)为10 dB，CPI处理脉冲数和来波信号载频参数同上。图5给出了输出信干噪比(Signal to Interference plus noise Ratio, SINR)与输入信噪比的关系曲线，考虑到自适应虚拟阵列和虚拟矩形阵列二维虚拟孔径与原真实阵列孔径基本一致，且大于虚拟L形阵列和虚拟十字阵列，较大的孔径尺寸会引起自适应虚拟阵列和虚拟矩形阵列形成较窄的主瓣波束，在信号、干扰方向固定时会改善系统的抗干扰性能，由图5可知，对于同样的输入信噪比，自适应虚拟阵列和虚拟矩形阵列的抗干扰性能优于虚拟L形阵列和虚拟十字阵列性能，虚拟矩形阵列的抗干扰性能略差于自适应虚拟阵列，原因在于虚拟矩形阵列的转换误差高于自适应虚拟阵列。

图5 输出信干噪比与信噪比的关系

4 结论

共形天线的阵元可灵活排布于卫星的表层，实现指定区域的探测任务。但这种天线构型对雷达探测信号处理方法的有效性和实时性提出了挑战。本文以二维圆孔径阵列为例，提出了一种自适应虚拟阵列变换方法，该方法利用自适应虚拟变换策略，以离线计算量为代价，大幅提升了来波DOA实时估计能力，可同时兼顾转换误差和虚拟孔径尺寸对探测性能的影响，因此在卫星深空探测领域有着重要工程应用前景。