包含细微缺陷的碳纤维增强复合材料管件结构弯曲性能表征

杨增钦，陈柏淼，尚福林*，侯德门，马小飞，王 辉

(1.南京电子技术研究所，南京 210039 ；2.西安交通大学航天航空学院，西安 710049；3.西安空间无线电技术研究所，西安 710100)

0 引言

纤维增强树脂基(CFRP)复合材料管件具有质量轻、高比强度、大比模量、耐高温、抗疲劳和阻尼性好等特有优异性能，在航天飞行器结构中广泛应用，是卫星环形空间开展开天线的主要构成部件[1]。

空间卫星长期在轨服役需要承受太阳热辐射和空间低温环境交替加热和冷却，引起其结构内部剧烈的温度变化。CFRP管件在实际的工作环境中，受外界温度、湿度等环境变化的影响，其内部可能出现基体微裂纹、微孔洞、纤维断裂和分层等损伤形式。这些内部损伤的演化和累积势必会影响材料结构的强度和刚度等力学性能，致使结构产生过大变形，甚至在服役中处于某种温度或者在低应力水平下就会发生断裂失效[2]，直接影响卫星天线在空间环境长期服役的可靠性。准确预测CFRP管件的结构力学性能需要深入研究损伤-失效机理。而复合材料的强度和刚度是材料内部损伤状态的宏观表征量，建立其各种损伤模式与复合材料结构刚度和强度性能的联系具有重要意义[3]。

迄今为止，国内外学者对复合材料内部各种损伤模式进行了详细分析，根据研究侧重点、影响因素不同，采用的研究方法基本可以分为两类，包括基于微观结构的细观损伤力学模型(MIDM)和基于宏观结构的损伤力学模型(MADM)[4]。细观损伤力学模型通过建立缺陷夹杂等细观模型，确定局部应力应变状态，来估算材料的整体性能，主要包括剪滞模型[5-8]、自洽方法[9-11]、变分原理[12-14]和数值计算方法[15-18]等。

宏观损伤力学又称为连续介质损伤力学(CDM)，其核心概念是采用内部状态变量代替均匀化连续体内的损伤实体，通过引入“连续性”概念来描述由于损伤引起的材料性能退化。Talreja[4，19，20]针对含有裂纹的复合材料层合板选取代表性体积单元(RVE)，定义二阶张量来表征RVE内的损伤实体，结合热力学方程，得到含损伤复合材料层合板的本构关系。之后Varna和Talreja等[21]通过试验测量不同铺设角空间电子技术2020年第1期为深入分析CFRP管件在空间长期服役的可靠性，本研究组在前期研究中[29，30]开展了大量的管件三点弯曲恒温蠕变试验(包括25℃、60℃、100℃、-20℃和-60℃五个恒定温度)和变温循环蠕变试验(包括-180℃～80℃和-60℃～100℃两个温度循环工况)。并且，基于实验室条件下获得的加速蠕变实验结果，根据时间-应力-温度等效原理和唯象蠕变模型，对设计工况下CFRP管件长期蠕变变形进行了预测。

为准确掌握CFRP管件在服役过程中的强度和刚度变化情况，本文继续对经历蠕变测试之后的CFRP管件开展研究，对管件弯曲性能和材料内部的缺陷情况进行实验测试和定量分析，深入探究CFRP管件的损伤-失效机理，构建管件材料内部损伤和力学性能退化的理论模型，以评价CFRP管件在长期受载后的承载能力。

1 管件弯曲性能测试与损伤测定

1.1 实验材料

该CFRP管件由M40J高模量碳纤维和B环氧树脂基体构成，纤维体积分数为60%，管件的铺层顺序为[+15/-15/0/90/0/-15/+15]，内径为24mm，壁厚范围为0.6mm～0.8mm。由于在-20℃和-60℃的低温蠕变环境作用时，CFRP管件没有发生明显的蠕变变形(见文献[29])，因此本文选取了经历?剾?25℃(室温)、60℃、100℃恒温和-60℃～100℃变温循环蠕变试验温度工况的管件(蠕变变形比较明显)进行测试。根据蠕变环境温度和施加应力水平的不同，将CFRP管件进行分类和编号，如表1所示。

表1 蠕变后的CFRP管件弯曲试验编号与尺寸参数

1.2 弯曲实验方法

参考复合材料弯曲性能试验国家标准GB/T1456—2005[31]和GB/T1449—2005[32]，结合CFRP薄壁圆管的特点，为避免试验过程中应力集中发生局部破坏，试验装置采用圆弧状的支座和压头(图1a所示)。

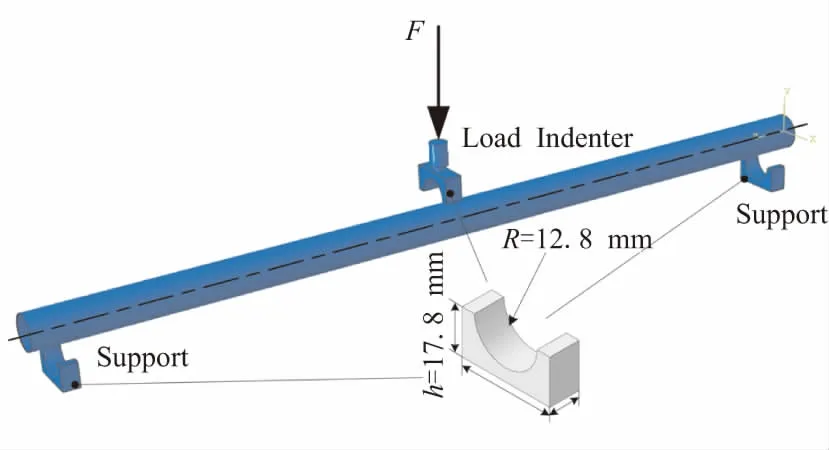
(a)Schematic diagram of the flexural tests device

(b)Photograph of the flexural tests device

为掌握在蠕变弯曲载荷作用后管件的承载能力，采用三点外伸弯曲试验方法的加载方式，且加载点与原蠕变试验保持一致，加载速率为2mm/min直至最后发生破坏，三点弯曲试验装置见图1b。

1.3 损伤观测方法

对弯曲破坏的CFRP管件开展进一步的缺陷观测。为方便进行管件的缺陷分析，选取距离弯曲破坏断面距离约10mm处的端面进行观测，主要观测管件端面受弯曲载荷的上下边缘部位(如图2所示)。并对截取的CFRP管件端面进行打磨、抛光处理，待处理完毕后在光学显微镜上进行微观分析。

1.4 CFRP管件弯曲试验结果分析

对蠕变后的CFRP管件开展三点弯曲试验，试验结果如图3所示。试样在加载开始至发生破坏前，载荷-位移曲线前保持良好的线性关系，在加载至临界状态时，试样承受的载荷值迅速下降，无法继续承载，呈现脆性断裂的特征。

按国家标准建议的材料力学方法计算管件等效弯曲模量[33]和弯曲强度[34]。

(1)弯曲模量E

(1)

式中F为弯曲加载点载荷，L为弯曲跨距，d1为管件外径；d2为管件内径，f为加载点挠度。

(2)弯曲强度σf

(2)

式中Fc为管件破坏时对应的临界载荷值。

1.5 CFRP管件内部缺陷定量分析

图4给出了典型CFRP管件试样的端面显微观测图像。可以看出，经历蠕变环境后，CFRP管件内部的缺陷主要包括微孔洞(Micro-void)和基体内的横向微裂纹(Transverse Micro-crack)。在弯曲载荷的拉压两侧内部损伤模式没有明显区别。由于长期受蠕变载荷的作用，管件结构内的微裂纹和微孔洞等缺陷呈现弥散型分布。其中基体内横向微裂纹在复合材料单层内沿着垂直于纤维方向演化，并垂直与铺层界面，微裂纹贯穿单层，长度为单层厚度；微孔洞具有不规则性，在管件内部呈现随机分布。

(a)Selection of the observation surface

(b)Selection of the observation points

图3 CFRP管件三点弯曲载荷-位移曲线

将观测到的两种损伤模式进行定量描述，得到CFRP管件的层合板孔隙率pv和单层内横向裂纹密度ρc。

(3)

(4)

上两式中Sv为观测面内孔洞面积，S0为观测总面积，nc为观测截面内横向裂纹总条数，k为观测面的总铺层数，l为观测截面总长度。

对微裂纹和微孔洞两种缺陷定量分析，统计得到管件内的孔隙率主要分布在0%，1.5%和2.0%三个量级。按公式(1)和(2)计算蠕变后的CFRP管件弯曲模量和弯曲强度，并将与管件的孔隙率和微裂纹密度对比，如表2所示。

从表中数据可以看出，随着内部缺陷的增加，管件的弯曲模量和弯曲强度有一定下降趋势。

下面尝试建立其损伤模型，以分析微裂纹和微孔洞对CFRP管件宏观力学性能的影响。

图4 CFRP管件观测截面微观形貌

表2 蠕变后的CFRP管件力学性能与损伤分析

2 损伤模型的建立

2.1 基体微裂纹建模分析

影响的问题时，认为含有基体裂纹的复合材料层合结构是损伤的基体与无损伤纤维的组合体(图5所示)，借助断裂力学理论，定义损伤变量，给出了因微裂纹引起的基体应力-应变关系式

(5)

(6)

式中a为裂纹的特征长度，Se=lb为选取RVE面积，这样D可以看作裂纹长度相对于RVE的大小。

假设微裂纹的长度和宽度均为单层板的宽度t，则损伤变量可以进一步转换为裂纹密度函数

(7)

其中ρc为基体微裂纹密度，表征单位长度基体包含微裂纹个数。

根据材料柔度矩阵定义，可以得到含有均布微裂纹的基体的工程常数，其表达式为

(8)

式中Em1和Em2为含均布裂纹基体纵向和横向的弹性模量，Gm12和vm21分别为含均布基体的剪切模量和泊松比。

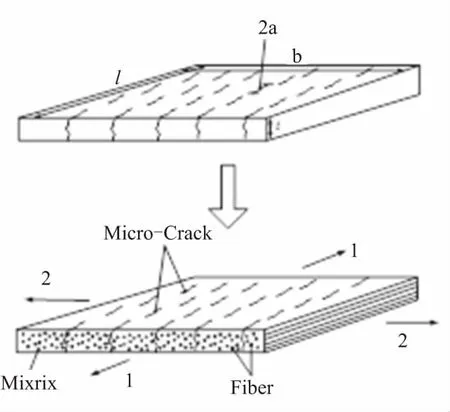
图5 含基体微裂纹的复合材料单层板

进一步运用Tsai-Halpin模型[35]可以得到含损伤单层板的工程常数：

(9)

式中Ef为纤维的弹性模量，vf为纤维的泊松比，Vf为复合材料中纤维的体积含量，ζ为材料常数，可以通过无损伤复合材料的工程常数确定，β1和β2为两个与材料性质相关的参数，可以由下式确定

(10)

对复合材料单层板，有柔度矩阵表达式

(11)

式中各个分量满足关系式：

(12)

由于材料刚度矩阵和柔度矩阵是互逆的，满足

[C][S]=[I]

(13)

式中[I]为单位矩阵，[C]为材料刚度矩阵，对公式(11)中的柔度矩阵求逆，便可得到单层板的刚度矩阵[C]。

对具有n个铺层的复合材料层合板，第i个铺层厚度为ti，铺层角度为θI，将单层板局部坐标系下的刚度矩阵转变为层合板总体坐标系下的刚度矩阵，有

(14)

式中[A]为坐标转换矩阵，进一步通过刚度矩阵组装，得到层合板的刚度矩阵

(15)

这样，先计算得到含有均布裂纹的单层板工程常数，再代入公式(11)～(15)便可以得到含裂纹损伤的复合材料层结构刚度矩阵 。

2.2 材料内微孔洞建模分析

材料在加载变形(弹塑性、蠕变等)过程中，会引起孔洞内部变形，直接影响材料的整体变形。复合材料内部含有的微孔洞在材料内部随机分布，认为其在宏观尺度上是宏观均匀的。在研究含有孔洞的复合材料的力学性能时，仍选择RVE模型来研究，RVE的尺寸远小于结构整体尺寸，可以认为是材料内的一个物理点。

对含孔隙损伤材料的本构关系，可表述为[3]

{σ}=[C]d{ε}

(16)

式中[C]d为含孔隙损伤材料的刚度矩阵，对材料内含有孔洞等内边界，材料内的应力和应变可做均匀化处理，即

(17)

式中上标a表示材料内部参量在体积内的平均值。

若材料内各点满足初始无损伤状态，则有

{σ}a=[C]0{ε}a

(18)

式中[C]0为无损伤材料的初始刚度矩阵。

Allen和Yoon[36]在对含缺陷材料均匀化处理、建立局部平均方程时指出，含缺陷材料的平均应变由施加在材料边缘的应变和内部缺陷表面的平均应变所决定，等于施加在材料边缘的应变减去缺陷内表面的平均应变

(19)

式中βij被称为Vakulenko-Kachanov张量，表征材料缺陷内表面的平均应变，沈浩杰[3]，Gudmundson[25，26]以及Lundmark[27，28]等在处理复合材料层合板含有裂纹缺陷问题时均运用到类似概念来定义损伤变量，来预测含缺陷材料的刚度变化。张量βij可以通过下式求得

(20)

(21)

对于复杂缺陷内表面，可以通过建立RVE，运用有限元方法加以确定。

对于选取体积为V，且内部为半径r的三维圆球形缺陷的代表性单元代表，缺陷内表面在三个方向的投影均为Sd=πr2，定义含有微孔洞的损伤矩阵[D]*为

[D]*=

(22)

并且，当式(22)中应变张量{ε}a分量为0时，对应项的损伤矩阵分量为0。显然，张量{β}满足关系式

{β}=[D]*{ε}a

(23)

将公式(18)代入到公式(23)中，得

{β}=[D]*[S]0{σ}a

(24)

式中[S]0为无损伤材料柔度矩阵，与[C]0为逆矩阵。结合公式(19)和公式(18)，有

{σ}a=[C]0({ε}-{β})

(25)

再将公式(24)代入到公式(25)，可得

{σ}a=[C]0{ε}-[C]0[D]*[S]0{σ}a

(26)

由于[D]*是对角矩阵，将公式(26)变形可得

{σ}a=(I+[D]*)-1[C]0{ε}

(27)

由于材料的内外力平衡，所以材料内部的平均应力{σ}a等于施加在材料上的应力{σ}，即

{σ}a={σ}

(28)

结合公式(16)，(27)和公式(28)，便可以得到含孔隙材料的刚度矩阵

[C]d=(I+[D]*)-1[C]0

(29)

3 损伤模型的验证

对平面应力问题，含复杂缺陷材料的有效弹性模量满足关系式

(30)

为验证本文建立的复合材料损伤分析模型的正确性，下面对含微裂纹和含均布微孔的材料刚度衰减进行预测。

3.1 含基体微裂纹的复合材料损伤模型验证

选取文献[23]中的试验和方法对本文基体裂纹损伤模型进行验证。如图6所示，铺层为[0/±θ4/01/2]s的复合材料层合板在±θ铺层内含有贯穿裂纹。

选取材料为玻璃纤维增强树脂基复合材料，组成的基体和纤维的材料参数如表3所示，纤维体积含量为Vf=52%，单层厚度为0.125mm。

图6 含微裂纹的[0/±θ4/01/2]s铺层层合板

表3 玻璃纤维/环氧树脂复合材料纤维和基体材料常数

运用本文的模型求解得到[0/908/01/2]s和[0/708/01/2]s两种铺层的层合板随裂纹密度增加的刚度衰减，并将计算结果与Singh和Talreja等的结果对比，如图7和图8所示。

图7 [0/908/01/2]s层合板刚度衰减

从图7和8可以看出，层合板的轴向弹性模量和泊松比随着裂纹密度的增加出现明显的衰减趋势，且随着裂纹密度的增加，复合材料层合板的有效模量衰减趋于平稳。本文的预测值与试验结果吻合较好，表明本文采用的模型可以应用于含基体裂纹的复合材料层合结构刚度预测。

图8 [0/708/01/2]s层合板刚度衰减

3.2 含微孔洞的复合材料损伤模型验证

为评估含微孔材料损伤本构模型的合理性和有效性，选用文献[37]的含均布圆形微孔的铝合金LY-12平板为分析对象。

如图9所示，在中心缺陷区域随机分布9，81，169个微孔，微孔直径d=0.5mm，缺陷区尺寸为L×W=12mm×12mm，板厚为t，材料弹性模量为71GPa，泊松比为0.33。

(a)9 Micro-voids (b)81 Micro-voids (c)169 Mi-cro-voids

对于二维平面问题，公式(22)中的损伤矩阵[D]*可变化为

(31)

式中Sd=nπdt，V=LWt

由材料孔隙率为pv=nπd2/(4LW)，则公式(31)可转化为

(32)

由此建立含微孔的RVE模型，施加初始应变，先计算孔洞内表面的平均位移，再结合公式(32)，(29)和公式(30)便可求得含圆形微孔缺陷材料的有效模量。

采用ABAQUS有限元软件，建立如图10所示的RVE有限元模型。根据对称性取1/4结构进行建模，对结构对称面上施加对称约束边界条件，分别施加沿x和y两个方向的初始应力和沿x-y方向的剪切应力。取孔洞表面的节点沿x和y方向的平均位移，运用本文模型来计算确定含缺陷材料的有效模量。

图10 含微孔的材料有限元RVE模型

将计算结果与于宁宇等[37]的试验结果对比，如表4所示。从表中数据可以看出，含不同数量微孔铝合金有效模量的预测结果与试验结果对比误差均在5%左右，表明本文建立的含微孔材料分析模型可以有效预测随着孔隙率的增加材料有效模量的下降。

表4 含微孔材料有效模量预测值和试验值对比

4 含细微缺陷的CFRP管件弯曲性能预测

4.1 含细微缺陷CFRP管件弯曲性能分析模型

从微观损伤分析结果可知，蠕变后的CFRP管件内部基体微裂纹和微孔洞呈弥散型分布。本文从细观结构出发，先确定微裂纹和微孔洞等细观缺陷对材料宏观性能影响后，再将其运用到CFRP管件的宏观结构分析中，以此来分析管件的刚度和强度。

针对CFRP管件内部缺陷分布的特点，本文作出如下均匀化假设：

(1)按统计得到的微裂纹密度ρc，将管件内的基体微裂纹均匀分布于层合结构的各个铺层内，且各铺层的内微裂纹贯穿铺层厚度；

(2)管件内的微孔洞为内部球形微孔，按孔隙率 等效分布在结构中；

(3)管件内部球形微孔洞具有相同的大小和形状；

(4)管件内的微裂纹和微孔洞在细观结构上呈现均匀性和周期性。

以此建立的含微裂纹和微孔洞的复合材料层合结构分析模型如图11所示。

图11 均匀化假设的CFRP层合板内部细观结构

结合本文含微裂纹和微孔洞损伤材料本构关系，建立含微裂纹和微孔洞两种细观缺陷的CFRP管件宏观弯曲性能的分析模型，主要步骤如下：

(1)结合公式(7)和(8)确定含有微裂纹的基体材料弹性模量和泊松比；

(2)应用Tsai-Haplin模型结合含裂纹损伤的基体和纤维得到单层板的材料常数；

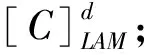
图12示意说明了CFRP管件弯曲性能分析模型的流程。

为确定含有微孔洞材料内表面平均位移，运用ABAQUS有限元软件建立图13所示的RVE模型。所选取的RVE为一立方体，边长L=0.8mm，球形微孔半径R=0.1mm，该RVE模型孔隙率为0.818%。考虑模型的对称性，取1/8结构进行建模和网格划分。

图12 含微裂纹和微孔洞的CFRP管件弯曲性能分析流程图

对于包含球形微孔的RVE模型，材料孔隙率为pv=4πR3/3L3，则公式(22)中的损伤矩阵[D]*可以转变为

(33)

图13 含球形微孔的材料复合材料RVE模型

4.2 CFRP管件弯曲强度判定准则

由于CFRP管件的破坏形式为沿轴向的脆性压缩破坏，而管件在弯曲加载点正下方具有最大轴向应变。随着管件内缺陷的增加，弯曲刚度不断下降，在相同载荷作用下，管件的最大轴向应变不断增大。鉴于此，本文将管件的最大轴向应变作为其承载能力评价指标，采用最大应变准则来计算含缺陷CFRP管件的承载能力。

(34)

认为管件达到最大承载能力。

4.3 含缺陷CFRP管件弯曲性能预测

建立CFRP管件的有限元模型(图14a所示)，管长为600mm，管件外径d1=25.49mm，内径d2=24.09mm，三点弯曲载荷作用跨距为L=580mm，根据本文模型引入微裂纹密度和孔隙率两种损伤参量，求解含损伤管件在弯曲载荷作用下的力学响应。运用模型求解得到不同微裂纹密度和孔隙率的管件载荷-位移曲线，如图14b所示。

(a)The FEM model of the CFRP tube

(b)The flexural load-displacement curves of

从图中预测结果可以看出，CFRP管件的弯曲模量和弯曲强度预测值与实验值吻合较好，表明本文的模型能够有效反映由于内部微裂纹和微孔洞引起的管件弯曲性能下降。

随着微裂纹密度和孔隙率的增加，管件的弯曲模量和弯曲强度呈现明显的下降趋势。由于本文模型建立于均匀化假设基础之上，并且复合材料内部可能发生纤维断裂或者分层等其它细小损伤，因此该预测值与部分试验值有一定偏差。

(a)Flexural modulus

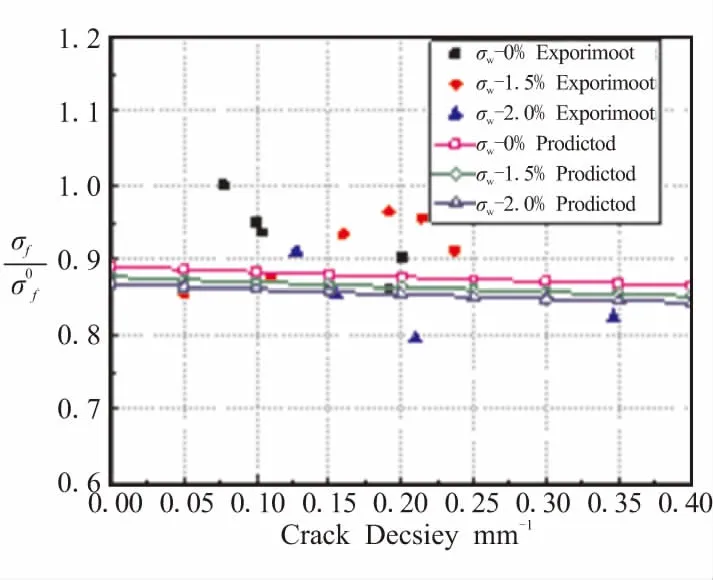
(b)Flexural strength

5 结论

(1)经历蠕变环境后的碳纤维增强树脂基(CFRP)复合材料管件弯曲模量和弯曲强度具有一定的下降趋势。通过微观分析发现，蠕变后的CFRP管件内部主要有微裂纹和微孔洞两种损伤模式，且细观缺陷呈现弥散型分布。

(2)基于Duan等提出的含裂纹复合材料损伤模型，定义含有微裂纹密度的损伤变量，建立了含有微裂纹密度的叠层复合材料本构关系。对材料内部含有微孔洞的缺陷进行分析，建立协同损伤力学模型，得到包含特定孔隙率的复合材料本构关系。

(3)结合CFRP管件的微观、细观和宏观结构多尺度分析，建立了含微裂纹和微孔洞两种缺陷的CFRP管件弯曲性能分析模型。假设微裂纹和微孔洞均匀分布在管件内部，将得到的含微裂纹密度和孔隙率的本构关系应用到CFRP管件的宏观结构分析，并用最大应变强度准则确定管件的极限承载能力；

(4)采用本文描述的方法计算了含微裂纹和微孔洞两种缺陷CFRP管件的弯曲性能。结果表明，考虑微裂纹密度和孔隙率两种损伤参量后，CFRP管件的弯曲强度和弯曲模量呈现明显下降趋势。