侧堰位置对生态河道直角折线堰泄流影响分析

邱 勇，陆怀茶，周鑫宇，杨泽文，陈玉斌

(云南农业大学 水利学院，云南 昆明 650201)

随着生态学的发展，人们尝试将生态与传统水利相结合，以使工程效益多样化[1-3]。董哲仁等[4-7]认为水利工程除了要满足防洪、抗旱等人类社会需求以外,还应充分考虑水工建筑物与周边整体环境、景观布置的相互协调及建成后对生态系统的影响。

作为生态水工建筑物的直角折线堰亲水设施，具有过流能力高、溢流效果美观等优点。能够查阅到的资料，仅针对前堰长度等于中堰长度(a=b)情况下的直角折线堰给出分析说明：张靖等[8]通过水工模型概化，分析了影响Z形薄壁堰过流能力的因素，针对一定堰高下的河渠宽度，给出了适用于中堰平行于河道轴线的直角Z形堰流量系数估算经验公式；常倩等[9]描述了直角Z型堰的水流流态、水流水面线及下游流速场等水流特性，利用统计分析方法给出流量系数估算经验公式。

1 试验方案

折线堰泄流能力受很多因素影响。主要影响因素有侧堰的平面位置(前堰长度a)、侧堰长度b、河渠总宽w、堰高P及堰顶水头H等。对于生态河道而言，为满足取水、防洪等需求，堰高一般不高，故试验研究仅针对一定堰高进行。

水工模型试验采用的直角折线堰侧堰长度b=112.5 mm，总宽w=150 mm(w=a+c)，上、下游堰高P均为100 mm，壁厚d=10 mm(见图1)。

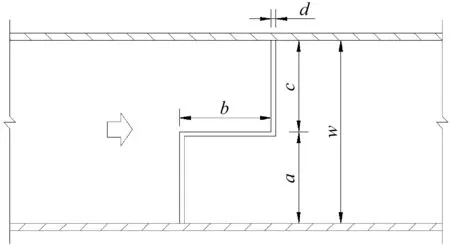
图1 直角折线堰平面布置示意图

试验研究保持侧堰长度不变，通过前堰长度变化得到不同侧堰的平面布置方案(见表1)。

表1 直角折线堰不同侧堰布置方案

2 试验研究成果

对于折线堰，在控制侧堰长度不变的情况下，不同侧堰平面位置是影响堰过流能力的主要因素。通过测试，得到不同试验方案下直角折线堰的过流能力，将其和文献[10]已经给出的相同堰高、堰宽情况下WES实用堰过流能力进行列表对比(见表2)。

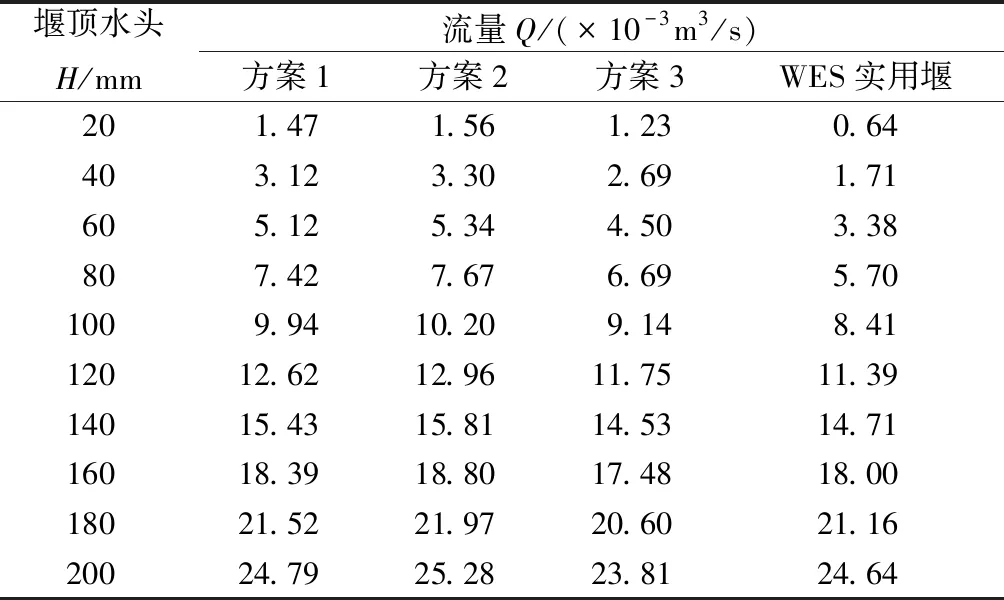
表2 不同折线堰方案和WES实用堰过流能力试验成果

由表2可知，当堰顶水头不超过140 mm时，直角折线堰的过流能力均大于WES实用堰；但当堰顶水头超过140 mm时，方案3(a=112.5 mm，c=37.5 mm)的过流能力小于WES实用堰。表明，直角折线堰的过流能力在堰顶水头不超过1.4倍堰高的较小水头时更大。

对比分析直角折线堰不同试验方案测试成果，方案2(侧堰位于河渠中部)过流能力最大，方案1(前堰长度a=37.5 mm)次之，方案3(前堰长度a=112.5 mm)最小。分析其原因，在于前堰长度的增加(后堰长度相应降低)，使得后堰的堰前来流不足以保证侧堰和后堰的充分过流。亦即，侧堰位置超过河渠中部(a>c)后，直角折线堰的过流能力出现较为明显的下降。

3 过流能力公式拟合

3.1 流量系数公式拟合

为了进一步说明不同侧堰布置对过流能力的影响，基于试验研究成果，对流量系数进行数学回归拟合分析(不考虑溢流前缘展长随堰顶水头增加的变化影响，计算时将过流宽度w视为定值)。直角折线堰过流情况类似于薄壁堰(特别是在低水头条件下)，随水头的增加，过流能力逐渐趋向于直线堰。不同试验方案下的流量系数根据堰流基本公式计算得到(见表3)。

(1)

式中：QM—模型流量，m3/s；

mM—模型流量系数；

wM—模型堰宽，m；

HM—模型堰顶水头，m。

表3 不同试验方案流量系数表

由表3可以看出，侧堰位置a及堰顶水头H的变化直接影响直角折线堰过流能力，故将流量系数m表示为a和H的函数：

m=f(a，H)

(2)

进而得到用变量m表示的直角折线堰流量计算公式：

(3)

根据表3所列数据，对公式(3)中的m、H进行回归分析。m、H回归分析可用幂函数、指数型函数等函数进行描述。幂函数形式简单，但其拟合相关性较低；指数型函数相对复杂，但相关性更高。综合比较分析后，选择指数型函数中的双指数衰减函数进行拟合，得到不同侧堰位置下m和H的关系图(见图2)。

从m、H回归分析图可以看出，试验点与拟合曲线吻合程度高，相关性良好。不同方案拟合成果参数值(见表4)。

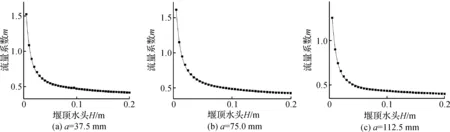
图2 m—H拟合成果

方案参数A0A1A2t1t2相关性a=37.5 mm0.416 711.508 770.373 960.007 330.050 830.998 94a=75.0 mm0.427 471.577 410.458 950.006 980.046 720.999 05a=112.5 mm0.406 171.227 530.266 520.007 150.041 080.998 68

由表4可知，不同方案下m与H具有很高的相关性。根据表列参数值可以得到不同试验研究方案下m、H的表达式：

(4)

(5)

(6)

由表4及式(4)—(6)可以看出，不同试验方案的拟合结果存在差异。为了进一步反映前堰长度a的变化对流量系数m的影响，将表4中的参数A0、A1、A2、t1、t2分别与a采用二次抛物线进行拟合分析。

参数A0、A1、A2分别与a拟合分析(见图3)。

参数t1、t2分别与a拟合分析(见图4)。

图3 A0、A1、A2与侧堰位置a回归分析

图4 t1、t2与侧堰位置a回归分析图

通过图3、图4可以看出，表4 所列参数与前堰长度a具有良好的相关性，拟合结果(见表5)。

表5 不同参数与侧堰位置a回归分析成果

将表5拟合得到的相关参数代入抛物线方程中，得到表4所列参数的拟合公式，进而可以得到m随a、H变化的流量系数计算公式：

(7)

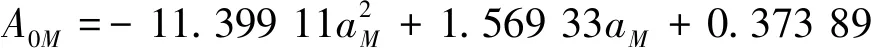
HM—模型堰顶水头，m；aM—模型前堰长度，m。

应用式(7)可计算试验方案不同侧堰位置(侧堰b长度不变、前堰a长度变化)情况下直角折线堰的流量系数(即过流能力)。

3.2 流量拟合公式验证

根据拟合公式(7)，分别计算不同侧堰位置下的过流能力，将其和试验研究成果进行比较(见表6)。

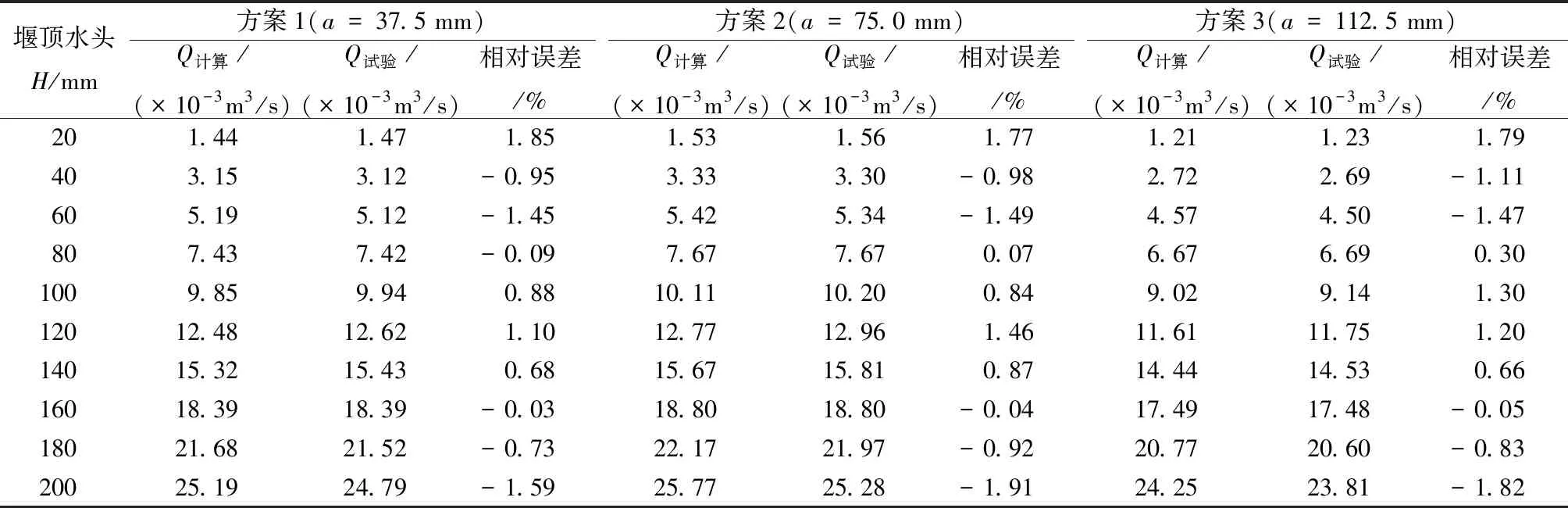
表6 试验成果与拟合计算结果过流能力对比表

从表6可以看出，拟合公式计算值与试验研究成果基本一致，相对误差最大值仅-1.91%。

进一步分析式(7)中的参数变化，堰顶水头变化时，前堰长度a介于63.0 ～64.5 mm时流量系数出现最大值(相应的直角折线堰过流能力最大)，侧堰位置已经比较靠近河渠中部。

前堰长度继续增加，直角折线堰流量系数开始下降：a=75 mm(1/2河渠过流宽度)时，过流能力仅下降1.13%。考虑到工程布置因素以及生态景观建设需求，可以认为侧堰长度一定，将其布置在河渠中部时，直角折线堰过流能力能够满足河渠行洪要求。

4 工程应用

按照重力相似准则，将试验成果几何比尺放大(以λ=20为例)后进行同样的拟合分析，所得到的流量系数和公式(7)的计算结果存在差异。

分析其原因，在于侧堰位置的变化，导致前堰长度a在拟合过程中存在不同的比尺效应，故不能把模型拟合结果简单放大后应用。因此对公式(7)进行变换，得到基于模型试验成果计划比尺放大后的流量系数计算公式：

(8)

式中：

(9)

(10)

(11)

(12)

(13)

HP—原型堰顶水头，m；aP—原型前堰长度，m。

即在实际工程应用中，可按几何比尺λ通过上述表达式对式(9)—(13)中的参数进行计算，得到原型流量系数mP，进而通过式(14)计算过流能力QP。

(14)

式中：QP—几何比尺放大后的原型流量，m3/s；

mP—几何比尺放大后的原型流量系数；

wP—原型堰宽，m；

HP—原型堰顶水头，m。

5 结 语

根据直角折线堰过流能力试验研究成果，分析拟合所得到的流量系数计算公式，当前堰长度逐渐增大至接近河渠宽度1/2时，其过流能力最大；而当前堰长度继续增加时，直角折线堰过流能力逐渐减小。此外，依据试验研究数据，经过数学回归拟合分析所得到的流量系数计算公式，经过几何比尺放大后，可用于指导一定堰高条件下，不同侧堰位置的直角折线堰过流能力计算。