一种n维组合混沌映射及性能分析

张雪锋，卫凯莉，姜 文

(1.西安邮电大学 网络空间安全学院，陕西 西安 710121；2.国家计算机网络应急技术处理协调中心，北京 100029)

随着网络通信和多媒体技术的快速发展，信息安全的问题也日益成为人们关注的热点之一[1]。数字图像作为多媒体信息的主要载体之一，相较于文本数据，具有冗余度高、像素相关性强和数据量大等特点。如何结合数字图像的特点实现相应的图像保护，成为信息安全领域的一个重要研究方向。

当前，主要的数字图像保护技术包括信息隐藏、数字水印和数字图像加密技术[2-5]。其中，数字图像加密技术通过将原始图像转化成无法辨别的噪声图像实现对图像的保护，能够有效防止数字图像内容信息的泄露，成为当前实现数字图像保密性的主流技术之一[6]。目前，图像加密技术主要包括圆形随机网格、格雷码、小波变换、斐波那契变换和混沌理论等[7-13]。混沌理论是美国气象学家Lorenz首次提出的[14]，其具有初值敏感性、随机性和遍历性等特点，与传统密码算法对性能的要求具有一致性，基于混沌的数字图像加密技术成为密码技术的一个研究热点。孙广明等[15]提出新的三维混沌系统并用于数字图像加密中。Rehman 等[16]提出基于混沌系统和DNA编码的彩色图像加密算法。Wang 等[17]提出一种基于Fisher-Yatess置换算法和Logistic映射的图像加密方案。Erdem[18]将一维Logistic映射应用于基于内容敏感的图像加密算法中，结果表明该算法可以有效防止数据泄露和噪声攻击。同年，张健和霍达[19]将混沌系统引入量子图像加密领域，提高了图像安全性。

和传统的混沌映射相比，改进的混沌映射或超混沌映射具有较复杂的混沌特性，相应的图像加密算法具有较好的安全性。Han[20]提出改进的Logistic映射，其李雅普诺指数恒大于0，有较好的随机性。Rajendran等[21]提出一种融合Sine映射到传统Logistic映射的二维Logistic-Sine映射(2DLSM)和二维Logistic映射(2DLM)，但分岔次数较多，系统进入混沌状态较慢。Lan等[22]提出基于Sine、Tent和Logistic映射组合的新的混沌方案，并将其应用到图像加密中，但存在密钥空间小、混沌系统不稳定的问题，而且随着分岔判定阈值的增大，分岔迭代次数增长过快的问题未得到解决，使得系统初值敏感性和安全性较差。

针对传统混沌映射在图像加密算法中存在安全性问题，提出一种n维组合嵌套混沌模型。基于传统混沌映射和改进的混沌映射构造不同的三维超混沌映射，通过实验仿真，分析组合混沌映射的Lyapunov指数、初值敏感性、相关性和功率谱等性能，并将其应用于改进的基于广义猫映射的较为经典的图像加密算法中，验证该加密算法的安全性能。

1 理论基础

混沌是非线性系统普遍存在的现象，表现为不确定性、不可重复性和不可预测性。Lyapunov指数是用来描述在混沌系统中，随着时间推移产生的相邻轨道发散或收敛现象的物理量，其值大于0，表征相邻轨道平均发散的快慢；值小于0则表征相邻轨道平均收敛的快慢。其个数与系统空间的维数n相同，若只有一个指数大于0，则系统是混沌的；若至少有两个指数大于0，则系统是超混沌的。大于0的指数越多，系统不稳定的程度就越高[23]。

1.1 Sine映射

Sine映射是一种经典的一维混沌映射，其结构虽然简单却可以产生复杂的混沌序列，定义式为

xi+1=μsin(πxi)。

(1)

其中：xi是迭代序列值，i取非负整数，x0∈(0,1)；μ是系统参数，μ∈[0,1]，当μ∈(0.87,0.93)和(0.95,1)时出现混沌现象。Sine映射的分岔图和Lyapunov指数如图1所示。

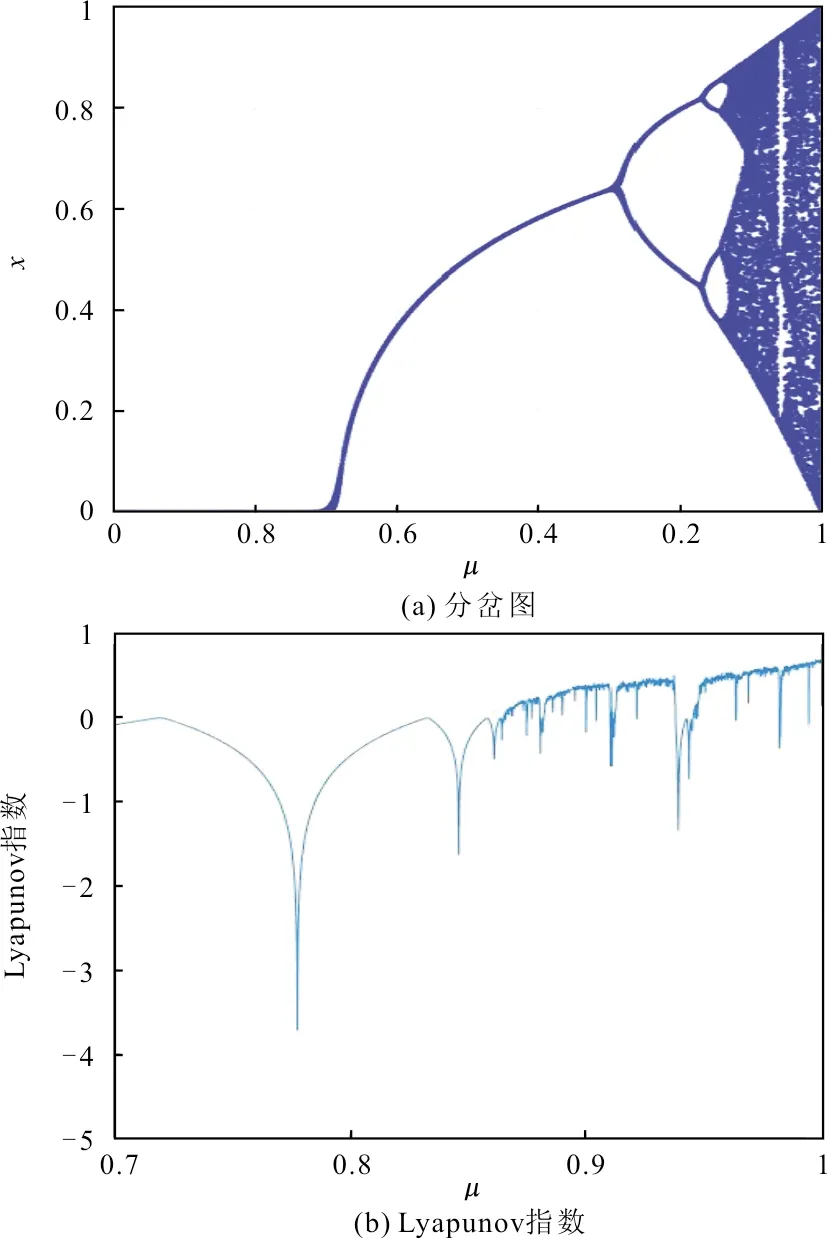
图1 Sine映射的分岔图和Lyapunov指数

1.2 Logistic映射

Logistic混沌映射被称为虫口模型，该模型最早被用来描述和预测昆虫数目的变化情况，由于其计算简单而被广泛应用，其定义式为

xi+1=μxi(1-xi)。

(2)

其中：x0∈(0,1)；μ∈[0,4]，当3.569 9…<μ≤4时，映射进入混沌状态。Logistic映射的分岔图和Lyapunov指数如图2所示。

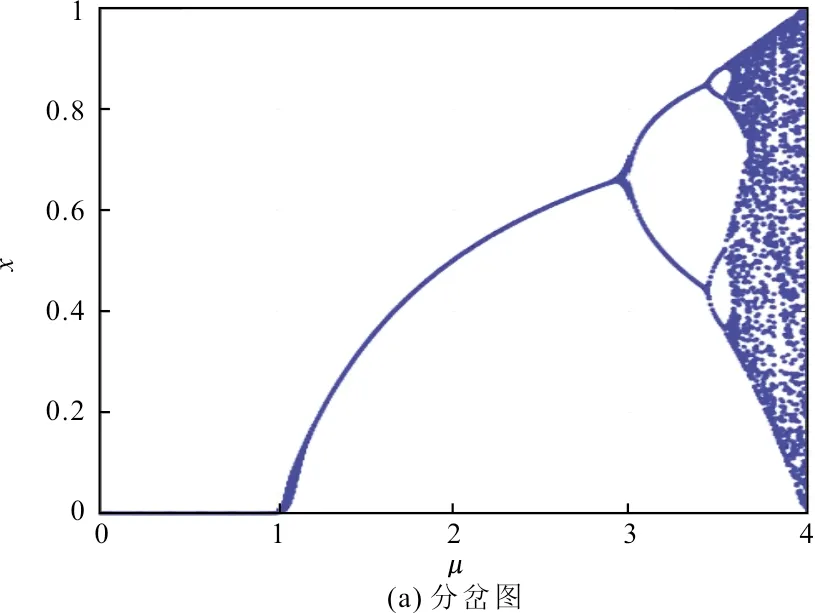
图2 Logistic映射的分岔图和Lyapunov指数

1.3 改进的Logistic映射

在Logistic映射的基础上，改进的Logistic映射[20]定义式为

(3)

当μ>0时，xi在[-2μ,2μ]内有满映射，其分岔图和Lyapunov指数如图3所示。

图3 改进Logistic映射的分岔图和Lyapunov指数

由图3可知，当μ>0时，改进的Logistic映射的Lyapunov指数恒大于0，说明改进的Logistic映射处于混沌状态。

2 n维组合混沌映射

通过具体分析混沌系统的Lyapunov 指数，设计一种n维组合嵌套混沌模型，根据此模型提出三维超混沌系统，以便对其进行性能分析。

2.1 一维组合混沌映射模型

为了提高一维混沌系统的复杂度，可将传统混沌映射进行串联、级联等操作[24]。Lan和He等人在2018年提出一种组合嵌套混沌映射的模型，经分析该模型有较好的混沌现象。以下用传统的混沌映射对不同组合混沌模型进行具体分析。

2.1.1 串联模型

假设混沌系统串联模型的计算表达式为

xi+1=L(xi)+S(xi)，

其中，L(xi)和S(xi)为传统混沌映射。

将初始混沌序列值进行微小变化生成x′，定义序列值在每次迭代时的微小变化量为|xi-x′i|，且有

又定义

则当xi趋近于x′i时，从|xi-x′i|到|xi+1-x′i+1|的变化率为

Lyapunov指数计算公式为

(4)

其中：f为混沌映射；t为迭代次数。根据式(4)可得串联系统的Lyapunov指数关系式为

则λτ1≥λL(x)，且λτ1≥λS(x)。

2.1.2 级联模型

假设混沌系统级联模型的计算表达式为

xi+1=L(xi)S(xi)，

其中，L(xi)和S(xi)为传统混沌映射,且混沌序列值xi∈[1,)。由式(4)得该系统的Lyapunov指数为

且有

2.1.3 组合嵌套混沌模型Ⅰ

Lan，He等人在2018年提出的模型是由混沌系统的串联和嵌套组成的，将混沌系统L(xi)和S(xi)进行嵌套，并用混沌系统M(xi)与嵌套后的系统进行串联，其表达式为

xi+1={L[S(xi)]+M(xi)}mod 1。

(5)

模型框图如图4所示。

图4 组合嵌套混沌模型Ⅰ

组合嵌套混沌系统Ⅰ的Lyapunov指数为

由串联模型中推导可知，当xi趋近于x′i时，S(xi)趋近于S(x′i)，有

则有

对于嵌套系统，可得

=λL(x)+λS(x)。

再由串联系统推导可得，组合嵌套混沌系统Ⅰ的Lyapunov指数为

λτ3≥λ′τ3=λL(x)+λS(x)，

λτ3≥λM(x)。

2.1.4 组合嵌套混沌模型Ⅱ

组合嵌套混沌模型也可将嵌套系统与级联模型中提出的级联系统组合，其中，嵌套系统L[S(xi)]和参与级联的系统M(xi)产生的混沌序列值xi∈[1,)，其表达式为

xi+1={L[S(xi)]M(xi)}mod 1。

(6)

模型框图如图5所示，

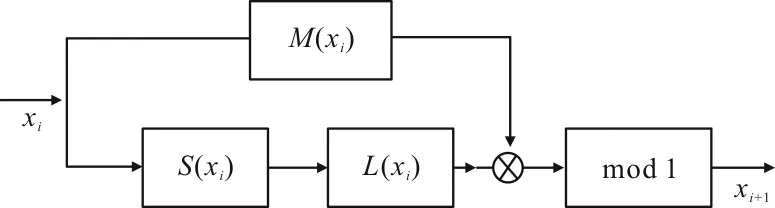
图5 组合嵌套混沌模型Ⅱ

组合嵌套混沌系统Ⅱ的Lyapunov指数为

λτ4≥λL(x)+λS(x)，

λτ4≥λM(x)。

由以上分析可得，不同类型的组合混沌映射在传统混沌映射的基础上，由Lyapunov指数表征的两个相邻点平均发散速度均有所提升，而在所给的传统混沌映射均处于混沌状态时，组合嵌套混沌映射的平均指数发散速度比串、级联组合混沌映射更快，具备更好的混沌性能。

2.2 n维组合混沌映射模型

为便于直接选取传统混沌映射或改进的混沌映射作为子映射，根据一维组合混沌模型Ι，可引申提出一种高维组合混沌模型，其第n(n仅用于区分不同维数)个表达式为

(7)

要计算高维组合映射的Lyapunov指数，先引入一般形式的指数计算方法。

若n维映射的一般数学方程为

(8)

则其雅可比矩阵式为

(9)

记初始值(x0,y0,…,z0),迭代t-1次得到t个雅可比矩阵为

J0=J(x0,y0,…,z0)，J1=J(x1,y1,…,z1)， ⋮Jt-1=J(xt-1,yt-1,…,zt-1)，

再记各个雅可比矩阵的特征值为α1i，α2i，…，αni，则可计算出

(10)

以二维映射为例，从宏观意义上对所提n维组合混沌映射的Lyapunov指数进行具体分析。由二维雅可比矩阵式和|αI-J|=0(其中I为二阶单位矩阵)可得

则有

≥λL+λS。

(11)

其中，W(x)对应于模型中维度变量的二次复合结构,即

与一维混沌映射Lyapunov指数的变化对应，高维混沌映射的Lyapunov指数有所提升。

2.3 三维组合混沌映射

根据2.2节中提出的高维混沌映射模型，由传统一维混沌映射或改进的混沌映射可组成不同的三维超混沌映射，定义式如表1所示。其中，L、S和IL分别表示Logistic映射、Sine映射和改进Logistic映射，均可作为子映射，组成表1中不同的超混沌映射。

表1 三维超混沌映射的定义式

Lyapunov维数[25]的计算公式为

(12)

图6 三维L-S映射的吸引子图

图7 三维S-L映射的吸引子图

图8 三维IL-S映射的吸引子图

3 组合混沌映射性能分析

为更好地分析组合混沌映射的性能，以下主要用三维L-S超混沌映射与三维猫映射和现已提出的其他组合混沌映射[21-22]在x维度的基础上比较各方面的性能。

3.1 Lyapunov指数

三维猫映射表达式为

(13)

三维猫映射的特征值为α1≈5.049，α2≈0.643，α3≈0.308，因此，Lyapunov指数分别为lnα1≈1.620>0，lnα2≈-0.442<0，lnα3≈-1.178<0。相比之下，所提出的三维超混沌映射比三维猫映射更早地进入混沌状态。图9给出文献[22]中性能较好的一维Sine-Tent-Sine映射(ST-S)和Logistic-Tent-Logistic映射(LT-L)组合混沌系统的Lyapunov指数和文献[21]中2DLM和2DLSM系统的最大Lyapunov指数。

如图9(a)所示，将文献[21]中β1用μ代替，绘出2DLSM和2DLM映射的最大Lyapunov指数图，由图9(a)可得在其混沌区间2.75≤μ≤3.45内，所提L-S映射的最大Lyapunov指数较大。同时在均采用嵌套结构的前提下，图9(b)中给出一维组合嵌套系统的Lyapunov指数，从图9(b)中可以看出一维ST-S和LT-L映射的Lyapunov指数较传统映射均有明显增长，与三维L-S映射的指数增长趋势保持一致性。但随着μ的变化，一维组合系统Lyapunov指数波动较明显，存在奇异点现象。这也正印证了提出的高维超混沌系统在Lyapunov指数方面具备更好的性能。

图9 不同组合混沌映射的Lyapunov指数

3.2 密钥空间

将三维L-S超混沌映射产生的序列用作加密密钥时，为保证加密安全性，其密钥空间应不小于2128。以此混沌系统参数和初值作为密钥，采用精确到小数点后15位的双精度实数表示，则密钥空间1015×1015×1015×1015×1015×1015=1090>>2128,可见足以抵抗穷举密钥攻击。不同组合混沌映射的密钥空间如表2所示。

表2 不同组合混沌映射的密钥空间

由表2可得，文献[22]中的混沌映射密钥空间为1030<2128，不能抵抗穷举密钥攻击，三维猫映射密钥空间为1045>2128，可抵抗穷举密钥攻击，文献[21]中的混沌系统密钥空间最大。而所提出的三维L-S混沌映射密钥空间与文献[21]中的密钥空间相当，可较好地抵抗穷举密钥攻击。

3.3 随机性

随机性是指由混沌系统自身产生的行为具有随机性，其完全源自确定性系统本身，与外在因素不相关。下面从序列分布和频数检验两个方面分析序列的随机性。

3.3.1 序列分布

将三维猫映射和三维L-S混沌映射在x维度分别迭代1 000次，得到混沌序列分布如图10所示。

图10 两种映射在x维度的序列分布

由图10可得，两种映射序列分布范围均随机分布在(0,1)区间内，说明提出的三维L-S混沌映射和三维猫映射都有较好的随机性。

为了进一步比较映射性能，首先将生成的混沌序列转化成二值序列，然后对相应的二值序列的随机性作进一步的比较分析。将混沌系统迭代t次，并定义序列{x1,x2,…,xt}所对应的二值序列{X1,X2,…,Xt}的取值为

(14)

以下对生成的二值序列相关性能进行分析。

3.3.2 频数检验

频数检验能保证二值序列中0和1的个数相等，这是二值序列具有随机性的必要条件。计算公式为[26]

(15)

式中：p和q分别表示二值序列中0和1的个数;N表示二值序列长度。表3给出三维猫映射和三维L-S混沌映射在x维度分别迭代10 000次的频数检验结果。

表3 两种映射x维度的频数检验结果

实验结果表明，三维L-S混沌映射产生的二值序列中0和1的个数基本相等，接近序列长度的一半，具备较好的频数检验特性。而三维L-S混沌映射生成序列χ2的取值数量级较小于三维猫映射的χ2值，说明三维L-S混沌映射生成的序列有更好的频数检验结果。

3.4 相关性

自相关系数和互相关系数是两个评价序列随机性能常用的统计量。设序列Xi的长度为N，则该序列的自相关系数[27]定义为

(16)

其中m为步长参数。自相关系数的值与步长m有关，当步长变化时，如果自相关系数变化越小，说明对应序列的随机性越好。

假设不同的两个二值序列X1i和X2i的长度均为N，则这两个序列互相关函数定义为

(17)

互相关函数取值越接近0，说明两个序列越互不相关，差异程度越大。

对于理想随机序列，自相关函数应为δ函数，互相关函数应为0。图11和图12分别给出两种混沌序列的相关系数变化图。由图可以看出，混沌映射生成序列的自相关系数和互相关系数均接近理想情况的计算结果。同时，三维L-S混沌映射与三维猫映射产生序列的相关性基本一致，都有良好的随机性。

图11 三维猫映射x维度自相关系数及x与y维度 互相关系数

图12 三维L-S混沌映射在x维度的自相关系数及 x与y维度互相关系数

3.5 初值敏感性

3.5.1 位变化率

将混沌序列迭代10 000次并生成二值序列，统计当初始条件变化为Δx0=10-6时，二值序列中0和1的变化情况[28]。计算公式如下

(18)

其中：r为初始条件发生微小变化时二值序列中0和1发生变化的个数；N为序列长度。位变化率越接近于50%，说明序列对初值越敏感。表4给出不同初始条件发生微小变化时三维猫映射、部分组合混沌映射和三维L-S混沌映射在x维度的位变化率情况。

表4 x维度混沌序列的位变化率

由实验结果可得，对于初始条件的微小变化，三维L-S超混沌映射和文献[21～22]提出的映射以及三维猫映射产生序列的位变化率相近，接近于50%，说明三维L-S混沌映射有较好的初值敏感性。

3.5.2 分岔迭代次数

假设混沌序列xi+1=f(xi)，在初始条件产生微小变化(初始条件分别为x0和x′0)时产生序列{x1,x2,…,χt}和序列{x′1,x′2,…,x′t}，给定分岔判断阈值φ，定义Ω=min{i||xi-x′i|>φ},则称Ω是混沌序列初始条件为x0和x′0时的分岔迭代次数[29]。

以下对三维猫映射和三维L-S混沌映射在初始条件变化10-6时进行分析，将混沌序列在x维度各迭代200次，并在区间(0,200)内产生200个取样点，分别比较在给定的不同阈值下其分岔迭代次数，实验结果如表5所示。

表5 x维度混沌映射分岔迭代次数

由实验结果可知，对应相同的分岔判定阈值,文献[21]中的混沌映射所需的平均分岔迭代次数大于三维L-S超混沌映射所需的平均迭代次数，说明三维L-S混沌映射的分岔速度较快。三维猫映射和文献[22]中的混沌映射在分岔判定阈值较小时迭代次数明显小于三维L-S映射，随着分岔判定阈值的增大，分岔迭代次数的增长速度大于三维L-S混沌映射，相比之下三维L-S混沌映射在加密过程中能够较快地进入稳定的混沌状态。

3.6 平衡度

假设序列中0与1的个数分别为p和q，则该二值序列的平衡度定义为[30]

(19)

二值序列中0和1的个数越接近，平衡度越小，则序列随机性越好。

图13给出不同初始条件x0下三维猫映射和三维L-S超混沌映射在x维度迭代10 000次生成序列的平衡度分布情况。

图13 x维度两种映射平衡度分布

由图13实验结果可得，三维猫映射和三维L-S超混沌映射的序列平衡度都在0附近，说明序列具有良好的随机性。但三维猫映射在局部点处有陡增现象，表明在某些取值点生成的二值序列中0和1的个数相差较大，平衡度较差。通过比较，说明三维L-S组合混沌映射具有较好的随机性。

3.7 功率谱

一个信号的时域描述和频域描述是一一对应的，功率谱分析能够提供信号的频域信息。一个信号的时间序列看上去是不规则的，但其功率谱却可能呈现出规律性。若某动力学系统的频谱定长且连续可重现，则可确定该系统是混沌的。

对于时间序列xi(i=0,1,…,N-1)，根据式(16)计算其自相关系数Ca(m)。对Ca(m)进行离散Fourier变换，可得到Fourier系数和序列功率谱的计算公式[13]分别为

(20)

Qk=[Re(Pk)]2+[Im(Pk)]2，

(21)

其中：Fs为采样频率；k表示信号频率;Re表示取实部；Im表示取虚部。当功率谱具有单峰(或几个峰)，则对应周期序列；当功率谱无明显的峰值或者峰值连成一片，则对应混沌序列。两种混沌映射在x维度的功率谱如图14所示。

图14 x维度两种映射功率谱

实验结果表明，三维L-S超混沌映射的功率谱没有明显的峰值，且功率谱分析与三维猫映射的功率谱分析结果相似，说明与其混沌性能保持一致，也具有良好的混沌性能。

4 图像加密算法的应用

将提出的高维组合混沌映射应用到文献[32]较为经典的图像加密算法中，验证该系统具备良好的性能。其中，置乱、替换和扩散3个步骤中涉及的混沌序列分别对应三维L-S映射产生的序列值。选取Lena、Pepper和Boat彩色图像为测试图像，在R分量上的加解密图像及直方图如图15所示。

由图15可以看出基于高维组合混沌映射的加解密效果良好，加密图像直方图均衡，在密钥正确时可完整恢复出明文图像，说明该算法具备良好的安全性能。

图15 加解密图像及其直方图分布情况

5 结语

提出一种组合嵌套混沌模型，并以此为基础，基于经典低维混沌映射构造一种n维组合混沌映射。首先，从理论上分析不同组合形式混沌映射的Lyapunov指数，证明组合嵌套结构具有良好的混沌性能，其次，构建一种n维组合混沌映射模型，组成不同的三维超混沌映射。该组合映射通过扩展系统参数，可以有效地抵抗密钥穷举攻击，能改善混沌系统的复杂性和不可预测性。并以一种三维映射为例，主要在同一维度下对三维超混沌映射和三维猫映射及部分已提出的组合混沌映射进行性能分析，比较其在随机性、初值敏感性、相关性、密钥空间及功率谱分析中的性能优劣，最后，将提出的组合混沌映射应用在文献[32]提出的加密算法中，实验结果表明，该算法具有较好的安全性能。