基于神经网络的双X射线影像2D-3D配准算法

沈延延，冯汉升

1.安徽大学电气工程与自动化学院，安徽合肥230601；2.中国科学院等离子体物理研究所，安徽合肥230031

前言

现代医学中，放疗是恶性肿瘤的重要治疗手段。但放射线在轰击病灶的同时也会损害肿瘤组织周围的正常细胞，因此需要在治疗过程中使用图像引导放疗（Ⅰmage-Guided Radiotherapy, ⅠGRT）技术保证放疗精确程度，从而提高放疗对肿瘤细胞的杀灭效果，并降低副作用。2D-3D 医学图像配准技术可以进行患者摆位误差的计算，是极其重要的一环。

传统基于灰度的2D-3D 配准算法通常采用迭代优化的方式，通过搜索CT 的空间姿态并进行投影生成数字重建放射影像（Digital Reconstruction Radiograph,DRR），对比DRR图像与治疗中获取的X射线影像的相似度来判断当前CT 姿态与患者姿态间的差异［1］。由于DRR 图像的生成非常耗时，导致基于灰度的2D-3D 配准算法较慢。针对这一问题，Mu［2］采取块投影法，利用已有的DRR 图像帮助生成新的DRR 图像，减少DRR 图像生成的耗时。Tornai等［3］则将GPU 并行计算应用到2D-3D 配准中加快计算过程。而Pan 等［4］采取阈值分割来排除不感兴趣区域，减小计算数据的大小。Lei 等［5］则利用一对正交X 射线影像上两个单面板的粗配准结合作为2D-3D 配准初始化减小迭代次数。Ghafurian等［6］提出一种新的图像梯度概率密度直方图作为图像的特征，避免搜索优化6 个自由度的变换向量。晋青鹏等［7］分析解剖特征与DRR 图像变化的关系进行非刚性配准。同时随着深度学习的发展，Miao 等［8-10］最先提出并改进使用卷积神经网络（Convolutional Neural Network,CNN）从图像残差中计算CT 空间刚体变换参数。Pinheiro 等［11］则是将CNN 回归与传统方法结合到一起，迭代地对新生成的DRR 图像使用CNN 回归。Pei 等［12］同样使用CNN 并采取多尺度特征融合的方法综合提取局部和总体特征进行配准。

本研究提出一种基于CNN的双X射线影像配准方法，利用两个具有一定夹角的X射线影像在平面上的配准，将空间刚体变换参数的一部分转化为平面上的近似刚体变换，同时利用3个神经网络分组进行回归预测的方法简化2D-3D配准，从而达到快速进行2D-3D配准的目的。

1 方法

1.1 几何分解

模拟拍摄双X射线影像时的机械结构，建立如下空间坐标系O 及两个X 射线影像所在的平面坐标系O1、O2。其中射线源与射线间绕Y 轴的夹角为θre，且该两个射线都平行于平面X-O-Z。几何示意如图1所示。

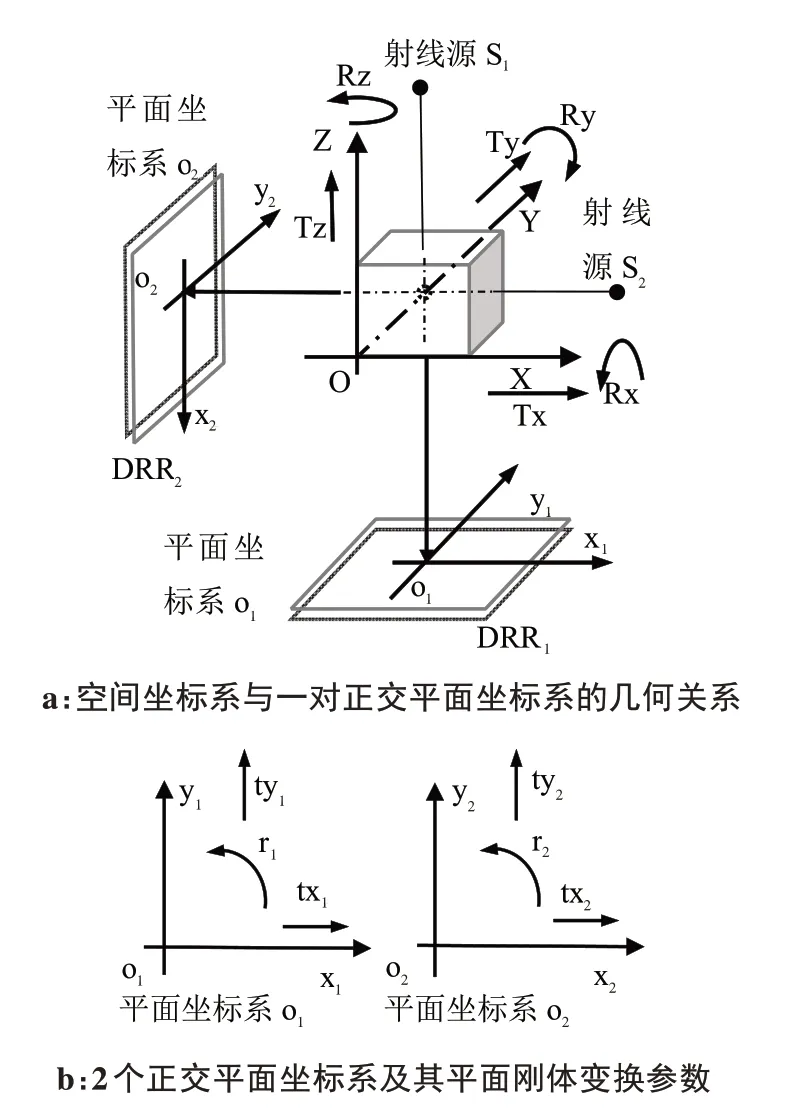
图1 空间坐标系与平面坐标系Fig.1 Spatial and plane coordinate systems

根据该几何关系可将空间刚体变换的6 个参数中的5 个（包括沿X、Y、Z 轴的平移Tx、Ty、Tz，以及沿X、Y 轴的旋转Rx、Ry）分解到两个X 射线影像所在平面坐标系中，反之也可由两个平面坐标系计算空间坐标系的Tx、Ty、Tz、Rx、Ry。

首先，从空间参数分解到平面参数：

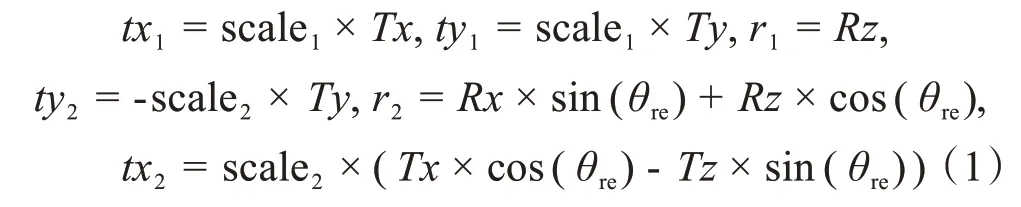
然后，从平面参数反演出除Rz以外的5 个空间参数Tx、Ty、Tz、Rx、Ry：

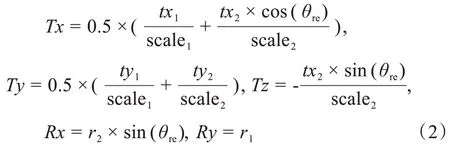
射线源到DRR平面的距离即源像距（SⅠD），射线源到等中心点的距离即源轴距（SAD），上述公式中放缩系数scale1与scale2的计算如下：

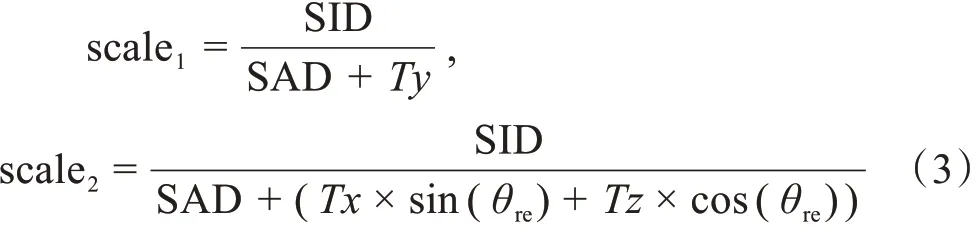
在该坐标系下，模拟拍摄一对夹角为θre的X 射线影像，生成两幅DRR图像，由坐标系分解可以得到在两个平面上的X-DRR 图像对配准结果，计算出空间参数的Tx、Ty、Tz、Rx、Ry。

1.2 分步配准

对应射线下的X-DRR图像对之间的差异主要由CT 姿态的空间变换造成，因此从X-DRR 图像对的残差到空间的姿态变换是存在着一个高度非线性的映射。而神经网络在理论上是可以无限逼近任意非线性函数的，因此本研究采用神经网络对空间刚体变换参数进行回归预测。为简化配准问题的复杂程度，将配准分解成两个步骤进行。由前文分析可知刚体变换参数中的5个组成元素反映在平面变换中，根据参数类型的不同将其分为两组分别进行回归，包含平面内参数Pin={tx1,tx2,ty1,ty2,r1,r2} ，平面外参数Pout={R2} 。

由于参数Tx、Ty、Tz、Rx、Ry并非独立作用在两个平面上，其中平移参数在一个平面上表现为平移，在另一个平面上为放缩。例如Tx在平面坐标系o1上表现为平移tx1，在平面坐标系o2上表现为放缩系数scale2。旋转参数在一个DRR 图像上表现为旋转，同时使得射线源到另一个DRR 图像像素点的光路所经过的CT体素点发生改变，进而造成对应DRR像素值改变以及图像轮廓的形变（如Rx与r2以及DRR1）。因此X-DRR图像对之间是一种非线性变换。当初始位置到目标位置的差值较小，即算法收敛范围较小时可近似成刚体变换。Pin是两个平面上X-DRR 图像对之间的近似刚体变换参数。

按难易顺序先后回归Pin和Pout，并且根据Pin回归结果对DRR 图像进行对应的刚体变换，进而尽可能地消除已知参数对图像的影响，使得在后续网络中仅包含未知参数造成的图像差异。其算法流程如图2所示。

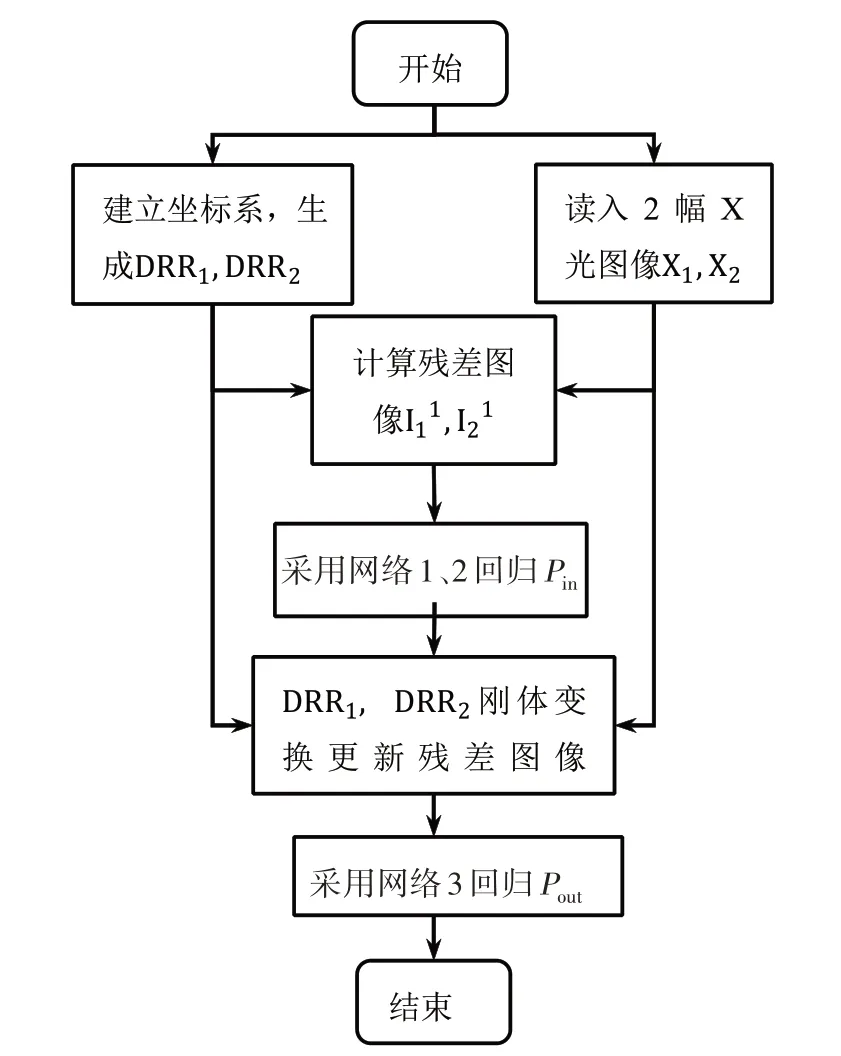
图2 分步回归Fig.2 Step-by-step regression

1.3 网络结构

在第1.2节中使用了3个独立训练的CNN回归网络。其中网络1、2的目的分别是回归两个平面上的参数，因此它们的网络框架完全一致。输入为X-DRR图像对的残差图像，为了减小输入图像大小，将512×512的残差图像分割为互有重叠部分的4个258×258的区域，重叠在一起后输入一个仅少量卷积层组成的扩展网络CNN-Pre。将扩增的特征图输入由Dense Block［13］组成的特征提取网络，并且每一个Dense Block的输入都是由之前所有的Dense Block的输出经过不同的池化层将特征尺寸统一后连接再经过1×1卷积层的特征融合操作得到。最后将提取到的所有特征进行全局平均池化，再把池化结果输入全连接层，输出患者摆位误差。网络结构如图3所示，网络1的CNN-Pre Block内部结构见表1。

网络结构经过前两个网络的回归，对DRR1、DRR2图像独立进行了刚体变换来消除已知参数的影响。由于前一步的回归精度问题，必然存在参数误差，而且空间刚体变换参数并非独立作用于两个平面上，故而在回归Pout前对两个平面上图像进行独立的刚体变换不足以完全消除已知参数的影响，即输入Pout回归网络的两个平面上的残差图像I1、I2中还包含Pin回归误差以及平面刚体变换带来的干扰。因此需要一个拟合能力更强的回归网络，在网络1、2的基础上进行改进出网络3。

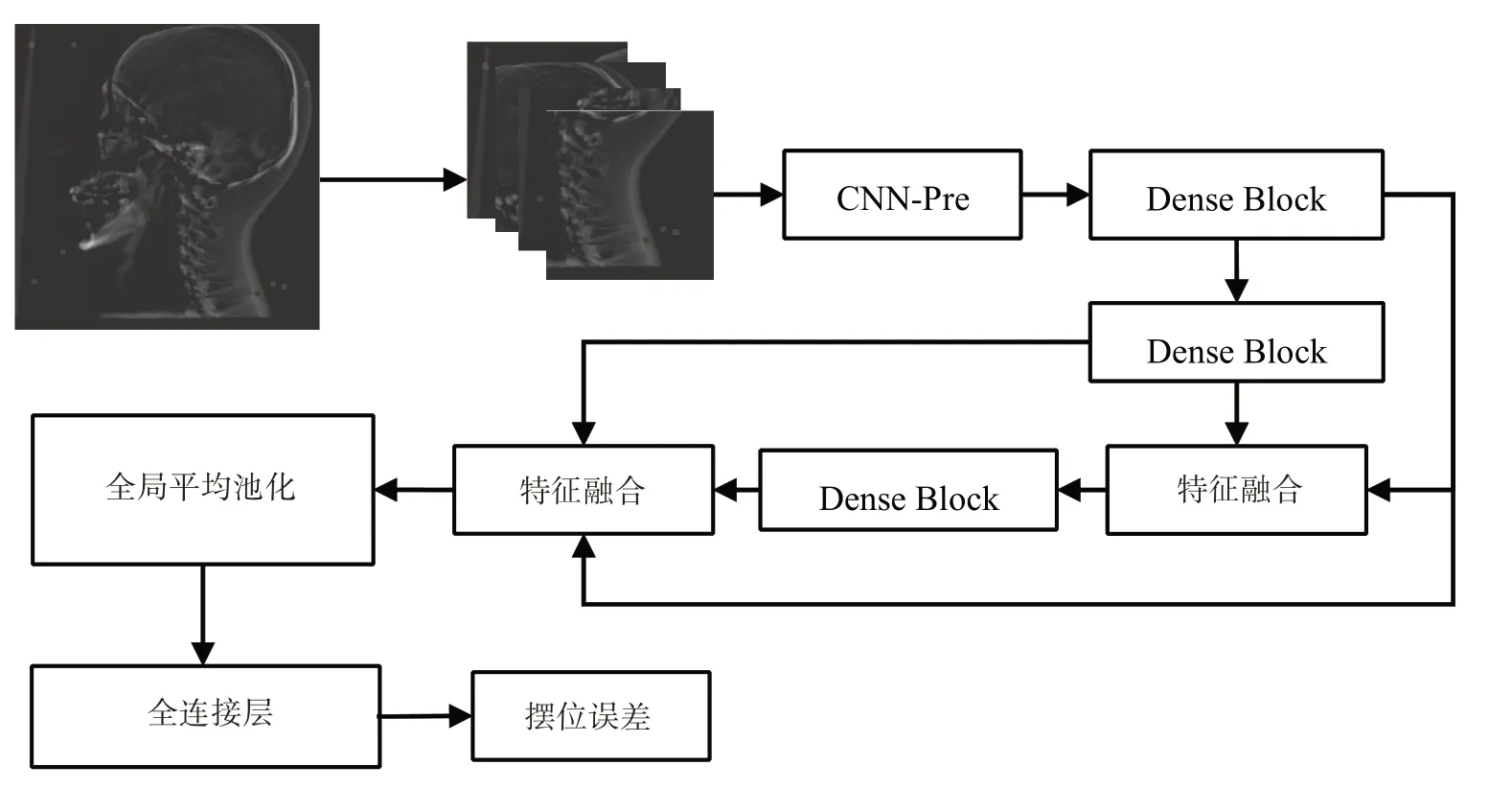
图3 网络主要框架Fig.3 Main architecture of network

通过对网络1、2 在其CNN-Pre 部分进行结构修改来提高该网络的特征提取能力，修改后的CNN-Pre如图4 所示。其中，Conv2D-1 使用深度可分离卷积［14］；Conv2D-2 使用1×1 的卷积核减少特征数量；Conv2D-4使用5×5空洞卷积增大感受野［15］；Conv2D-5使用1×1 卷积核进行特征融合；其它卷积核为3×3。所有卷积前都添加Batch Normalizetion［16］层，激活函数为ReLu［17］，同时Conv2D-1、Conv2D-2、Conv2D-3、Conv2D-6使用2×2的平均池化。

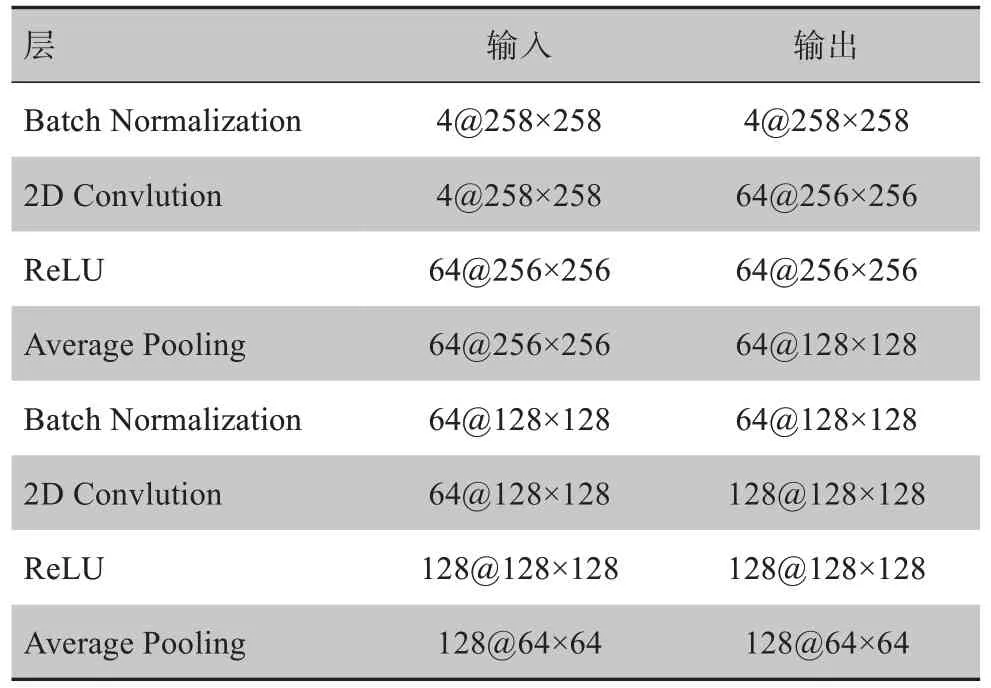
表1 网络1的CNN-Pre Block内部结构Tab.1 Internal structure of CNN-Pre Block of network 1

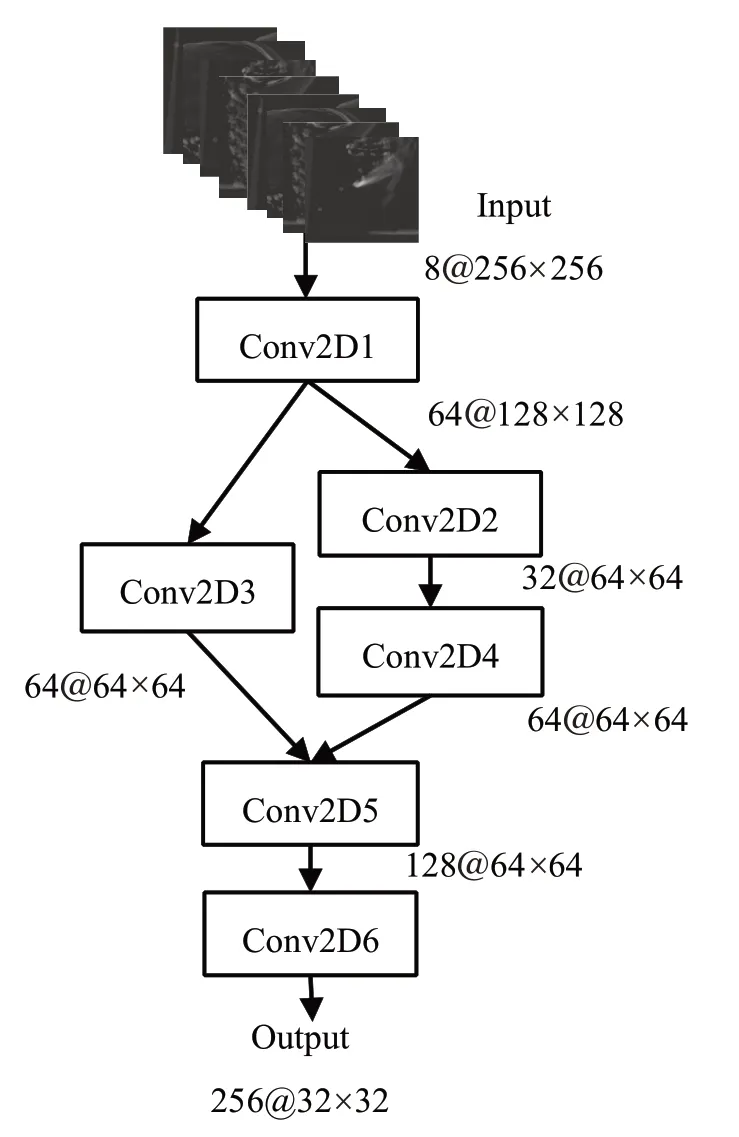
图4 网络3中CNN-Pre结构图Fig.4 Structure of CNN-Pre of network 3

对于网络3 的输入图像需要进行预处理。首先去除两个残差图像四周边缘的32个像素宽度丢弃平面变换时在图像边缘引入的误差，然后再按照相互重叠32 个像素宽度的方式将剩余图像分割为4 个256×256 的区块，最后将两个平面上残差图像分割结果重叠为8@256×256，作为网络的输入图像。

2 实验

2.1 数据获取

在本实验中，采用DRR 图像模拟X 射线影像以获取准确参数用于训练。针对CT 尺寸为512×512×283，物理尺寸为（400×400×283）mm3的头颅CT 生成约26万组训练数据［18］。每一组数据包含在初始参数下生成的2幅DRR图像，在目标参数下生成的2幅模拟X 射线影像，所有图像大小都是512×512。设置两次拍摄时，绕Z 轴旋转的夹角为90°。取95%的图像数据作为训练集，剩余部分作为测试集。

2.2 实验结果

在上述训练数据下，在显卡为Tesla P100、CPU为Ⅰntel E5-2680 的服务器上使用深度学习框架Pytorch 0.4 编写训练。训练轮数Epoch 为32，每一轮中不重复地随机抽取的mini Batch大小为64，直到所有组数据都被使用过。训练中采取神经网络常用的Adam 优化方法［19］。损失函数采用L2 范数即刚体变换参数的均方误差。网络1 训练结果如图5 所示，其中学习率LR按式（4）进行调整。

为对比该配准方法的配准效果，所采用的对比算法为CUDA 加速迭代式的双X 射线影像配准（CUDA）。在第2.1 节所述头颅数据上1 万多幅测试图像中随机挑选50组，配准结果如表2所示。

其中采用的配准结果衡量标准为mTRE［20］与配准参数平均误差ME。

mTRE计算方法如下：

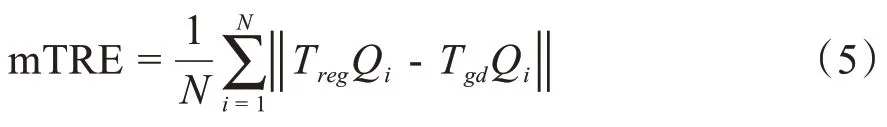
取CT 中包含N个点的点集Q，计算其在配准结果的变换Treg与目标真实变换Tgd下的对应点距离误差均值，同时取CT 数据的物理尺寸长度1% 即2.83 mm 作为配准成功的标准。ME作为配准精度衡量标准，ME(P)计算方式如下：

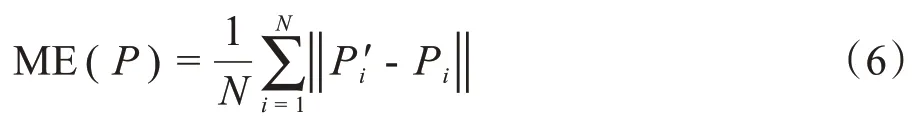
P与P′是包含N个平移配准参数的向量，分别为配准参数与真实参数，其中平移PT=[Tx,Ty,Tz]，旋转PR=[Rx,Ry,Rz]，分别计算平移与旋转的ME。

2.3 分析

实验结果表明，本文方法在ME 度量下，其平移参数回归误差为0.047 mm，相对迭代算法下降了81.20%；旋转参数回归误差为0.057，相对CUDA 算法下降了68.51%，有显著提升。在mTRE 标准下，本文方法配准误差为0.462 mm，仅为CUDA 算法的32.32%。因此本文方法的配准精度在多个指标下相对传统算法都有较大提升。

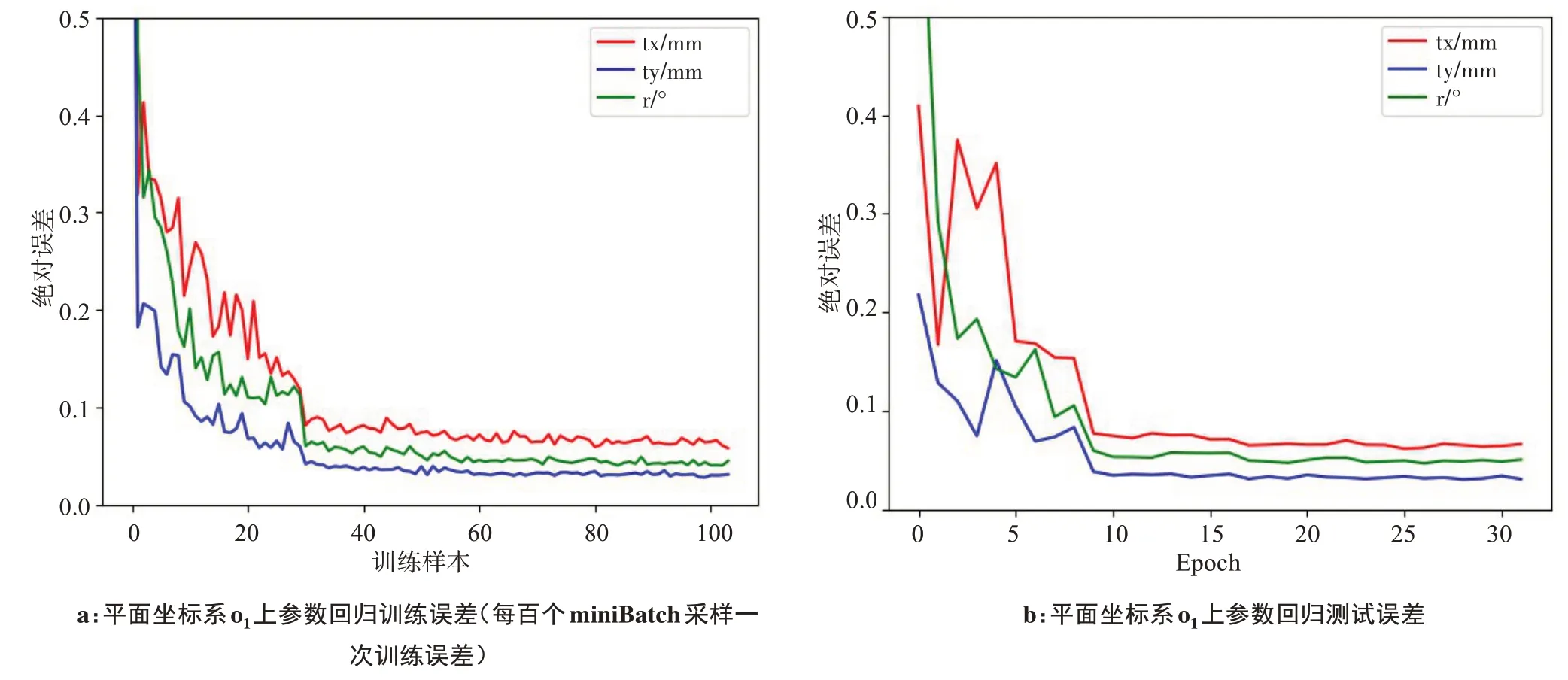
图5 网络1训练结果Fig.5 Training result of network 1

表2 实验结果Tab.2 Experience results

X-DRR 图像间的相似性度量是关于空间变换参数的高度非线性函数。因此在传统迭代优化过程中非常容易陷入局部最优值，造成配准误差较大。而由于采用了CNN 回归的方式，本文方法在配准过程中没有传统迭代算法的优化过程，依靠神经网络强大的拟合能力，从训练数据中寻找X-DRR 残差图像到空间参数的映射关系；又由于空间参数分步回归，进一步简化了这种映射，使得神经网络能回归出更加精确的最优解。

在50 组随机数据中平均耗时仅为0.04 s，即达到25FPS 的处理速度，远快于CUDA 方法，达到实时配准的标准。对于训练好的神经网络，在配准中仅需要对于残差图像做一次单向的运算，无需迭代生成DRR 图像和计算图像相似度，从而规避了传统迭代优化算法中最耗时的部分，具有非常快的配准能力。

3 结论

在ⅠGRT 系统的工作中，2D-3D 配准速度的快慢直接影响患者的治疗体验。本研究提出的利用双X射线进行空间坐标分解，简化空间坐标系变化与X-DRR残差图像映射关系；利用含有Dense Block 结构的CNN 的强大非线性拟合能力，分步回归出空间刚体变换参数。相对基于灰度的迭代优化配准算法，在配准精度和速度都有明显提升，尤其是其配准速度已经达到实时配准的标准，在临床治疗中具有一定实用潜力。