有限字符输入下基于截断速率的安全空间调制天线选择算法

丁青锋，奚韬，杨倩，丁旭

（华东交通大学电气与自动化工程学院，江西 南昌 330013）

1 引言

在多输入多输出（MIMO,multiple-inpit multiple-output）系统中，空间调制（SM,spatial modulation）作为一种有效的方法，可以在空间复用和空间分集之间取得良好的平衡[1]。不同于传统的MIMO 技术，SM 在每个时隙中仅使用一个有源发射天线，这意味着只需要一个射频链路就可以大大降低系统的硬件成本[2-3]。同时，SM 系统的特殊结构具有良好的稳健性，可以减少信道间干扰（ICI,inter channel interference），提高能量效率[4]。但是，大部分SM 系统要求发射天线数必须为2 的整数次幂，如果配备自由的发射天线个数，将需要通过算法选择出SM 的天线组合。

发射天线选择（TAS,transmit antenna selection）通过计算性能指标筛选出最优的天线组合，能够有效提高SM 系统的性能，因此成为热点研究课题[5-10]。文献[5]首先提出了最优容量天线选择和欧几里得距离优化天线选择（EDAS,Euclidean distance optimized antenna selection）这2 种TAS 方法，改善了SM 系统的安全容量性能，但是遍历所有的天线组合给发射端带来了很高的复杂度。文献[6]提出了一种新的等效于EDAS 的准则，该准则以矩阵降维为基础，在能够达到EDAS 相同性能的同时降低搜索复杂度。文献[7]通过对可分解正交振幅调制符号集合的信道进行正交三角分解，可以减少计算汉明距离的次数，从而降低算法的复杂度。

在考虑窃听者的场景下，通过加入物理层安全技术可以大幅度提升系统的安全容量[8]。文献[9]利用从发射机到合法接收机的信道状态信息（CSI,channel state information）来重新定义发射天线的索引，从而提高系统保密速率（SR,secrecy rate）的性能。文献[10-11]分析了多天线目的地和窃听者接收机空间调制的SR，通过联合信号和干扰传输而不需要窃听者CSI 的典型要求来研究安全速率。文献[12-13]将人工噪声（AN,artificial noise）压缩到所需信道的零空间以干扰未知的窃听者。文献[14]基于最大化安全容量设计AN，首先将AN 矢量安排在合法接收者信道的零空间上；然后利用波束成形技术将AN 矢量设计与窃听者信道共线，以最大化对窃听者的噪声。这样的物理层设计可以保证在不影响合法接收者的同时，大大降低窃听者的误码率性能[15-16]。文献[17]将天线选择算法与人工噪声技术结合，以得到MIMO 系统更好的安全性能。其理论和仿真结果表明，联合天线选择算法和人工噪声技术也能够有效地增强SM 系统的物理层安全。文献[18]针对有限字符情况下的安全SM 网络提出了2 种新的TAS 方案——基于最大化保密速率(Max-SR,maximum SR)和基于信漏噪比（SLNR,signal to leakage noise ratio）方法的天线选择算法，其中基于SLNR 的天线选择方案以极低的复杂度展现了出色的SR 性能。在文献[18]的基础上，文献[19]引入截断速率，用于进一步优化功率分配因子，并通过推导截断速率的上下界作为凸优化的函数，基于最大化SLNR 和AN 与泄漏加噪声比（ANLNR，AN to leakage plus noise ratio）进行凸集求解得到功率分配因子。

目前，基于优化安全性能的大多数TAS 方法普遍存在复杂度高和无法得到功率分配因子解析解的问题，而SLNR 算法的SR 性能在高信噪比区域不够好，因此，本文通过直接处理截断速率（COR,cut-off rate）表达式用于发射天线选择，并求解次优功率分配因子从而优化SR 性能。首先，经过理论推导，得到系统COR 的表达式。然后，基于最大化COR 表达式提出一种基于COR 天线选择算法，该算法通过遍历搜索所有可能的天线组合筛选得到最优的发射天线组合，从而得到最大化的保密速率。另外，针对传统算法复杂度较高的问题，本文提出基于列范数之差的搜索算法，将对应于矩阵范数的遍历组合问题简化。所提算法首先对矩阵范数进行按列展开，然后对合法接收者和窃听者信道对应的列范数作差，筛选出最大差值对应的天线，形成最优的天线组合，从而极大地降低了复杂度。同时，将AN 技术与天线选择算法相结合，将AN 矢量映射在合法信道的零空间，从而进一步提升安全SM 系统的保密速率。仿真结果表明，与基于SLNR 和基于Max-SR 这2 种TAS方案相比，本文提出的改进的基于COR（ICOR,improved COR）的算法是对闭式表达式进行直接简化，相比于SLNR 具有更好的SR 性能和相同的低复杂度。另外，通过简化之后的闭式表达式，本文基于SM 系统特殊性计算出对应的次优功率分配因子，可以实现更高的SR 和更低的误码率（BER,bit error rate）。

2 系统模型

2.1 空间调制系统

考虑在安全空间调制系统中，发射端Alice 配备了Nt根发射天线，合法接收者Bob 具有Nb根接收天线，非法窃听者Eve 具有Ne根接收天线。当Nt不是2 的整数次幂时，必须从Nt根发射天线中选择根天线负责发射调制符号，以将信息比特全部映射到天线索引序号。根据排列组合的知识，发射端总共有种组合模式，记为ψ={ψ1,…,ψk,…,ψL}，其中 ψk(k=1,2,…,L)表示所有天线组合中的第k 种组合。在每个时隙中，信息位被分为两部分，分别包含m 位和n 位。其中，m位用于从发射天线中选择一个激活的天线，通过调制将信息映射为天线的序号。n 位用于从M 进制信号星座图中选择幅度相位调制符号。可以得到，频谱效率为每通道lbNaM=m+n位，其中，lbNa位用来选择激活天线，其余lbM 位用来选择星座符号。

人工噪声和符号需要分别进行调制，并通过天线选择算法分配给激活的天线。发射调制符号的天线带有天线序号映射，可以承载一部分信息，发射人工噪声的天线则不带有任何信息。发射端激活第i 根天线发送的信号矢量记为x，类似于文献[20]中的安全SM 系统保密传输模型，引入AN 后的发射信号可以表示为

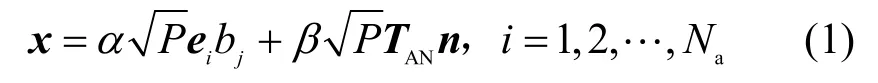
其中，α ∈[0,1]表示发射符号的功率分配因子，β ∈[0,1]表示发射 AN 的功率分配因子，满足α2+β2=1；P 表示总的发射功率；ei表示单位矩阵的第i 列；表示Na×Na的单位矩阵；bm表示lbM 阶星座图的第m 个输入符号，bj表示lbM 阶星座图的第j 个输入符号；TAN表示AN 矢量的投影矩阵；n～CN(0,)表示随机AN 矢量。因此，Bob和Eve 的接收信号矢量yb和ye分别表示为

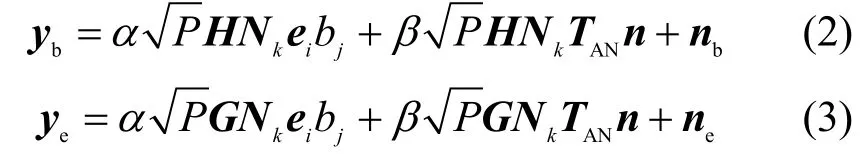
假设Bob 已知信道矩阵H 的信道状态信息，则最大似然检测（MLD,maximum-likelihood detector）算法如式(4)所示。

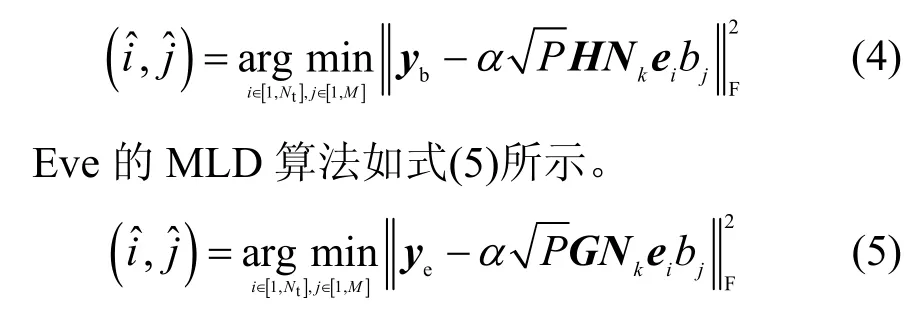
2.2 人工噪声

本文将AN 投影到合法信道的零空间上，从而使AN 对窃听者产生影响的同时不干扰到合法接收者接收信号，即HkTAN=0。则AN 投影矩阵 TAN可以表示为[21]

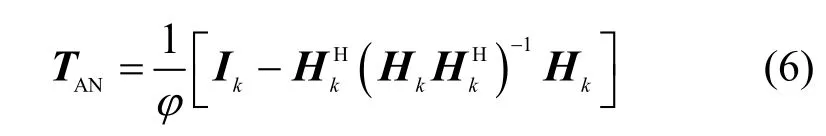
3 天线选择算法

通过TAS 筛选出使SR 最大的天线组合，由于SR 的闭式表达式难以获得[22]，本文提出一种基于COR 的天线选择算法。同时，利用基于矩阵范数之差策略进一步降低所提出的算法中天线选择的运算复杂度。

3.1 保密速率

根据式(2)，yb的条件概率分布函数可以表示为

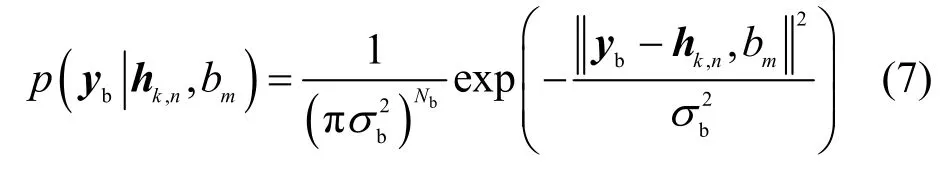
由于n 和m 是均匀分布的，因此yb的概率密度函数可以表示为[23]

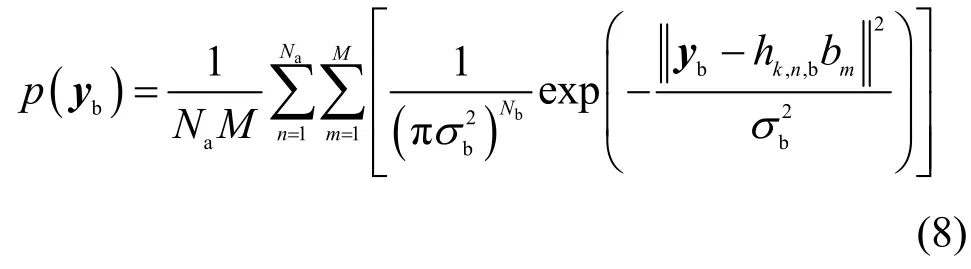
对于给定的信道，Alice 和Bob 之间的瞬时互信息可以写成如式(9)所示的形式。

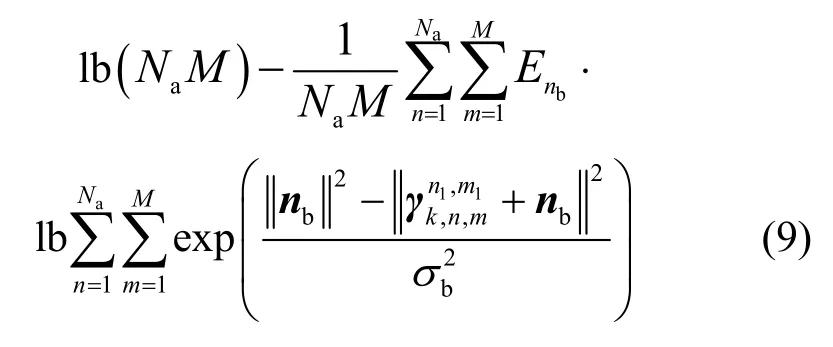
类似地，Eve 端能够获得的互信息为

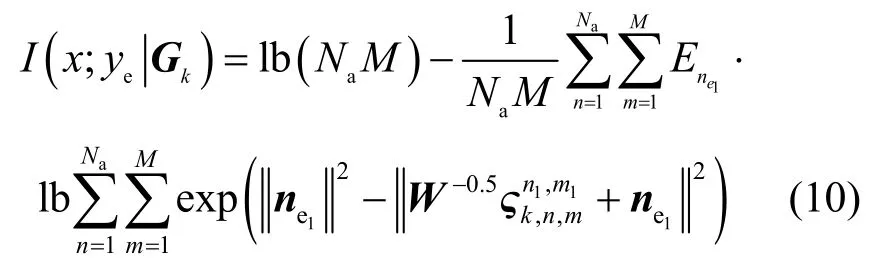
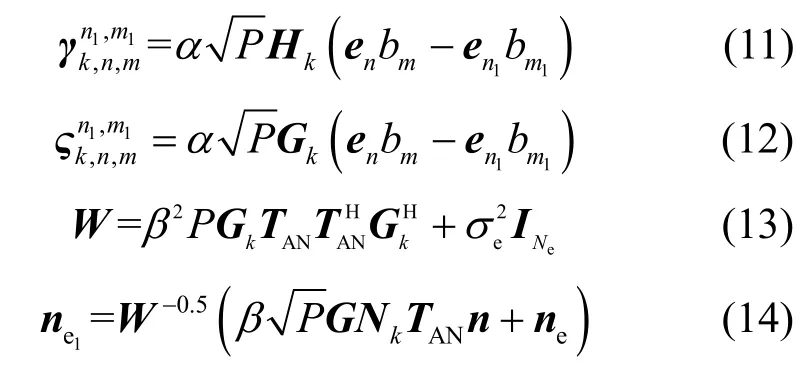
其中，W 是式(3)中ye的最后两项的协方差矩阵，为带有的新噪声矢量。

对于式(6)而言，由于n 是时变的干扰项，因此MLD 算法的检测性能会大大降低。利用平均保密速率来衡量系统的安全性能，可以表示为[24]

3.2 截断速率

由于缺少SR 的闭式表达，因此很难直接通过TAS 方法设计有效的最大SR 方法。尽管研究人员提出了一些传统的方法来提高SM 系统的性能，但是高复杂度限制了其在实际SM 系统中的应用。鉴于此，应用于传统MIMO 系统的具有紧密形式的COR 可以借鉴于SM 系统中，即采用一种通过基于最大COR的方案作为最大化SR 的有效指标[25]，如式(16)所示。

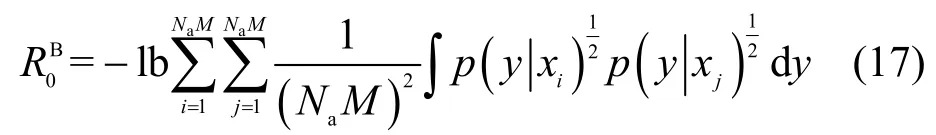
式(17)可以视为Bob 与Alice 互信息的有效下限。利用式(2)和式(9)，yb的条件概率密度函数可以表示为

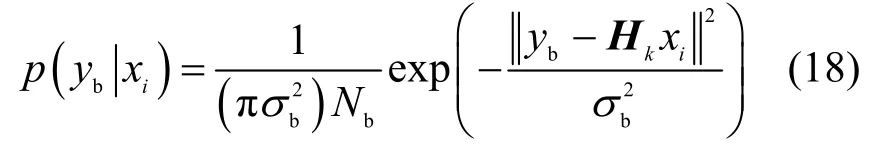
将式(18)代入式(17)中，经过推导，得到Bob的瞬时截断速率的闭式表达式为

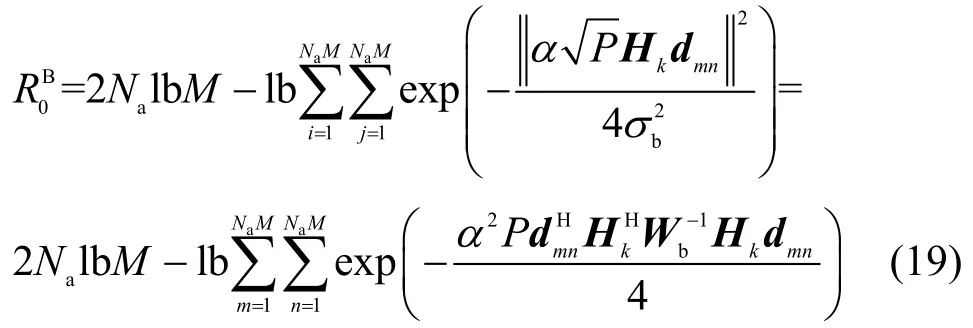
其中，Wb是式(2)中的干扰加噪声协方差矩阵。根据推导结果，得到类似的Eve 瞬时截断速率的表达式为

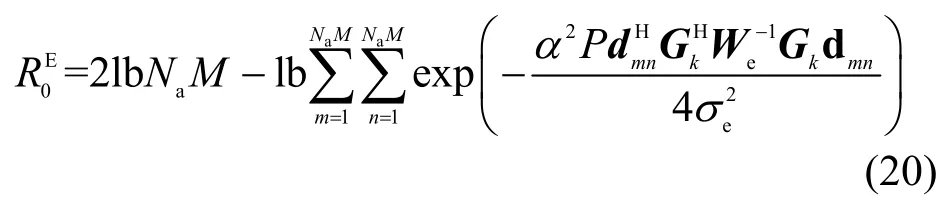
其中，We是式(3)中的干扰加噪声协方差矩阵。一旦获得了发射天线组，就可以使用式(15)评估SR。由于和是Hk和Gk的函数，因此可以选择一个最大的TAS 方案，该方案可以转换为

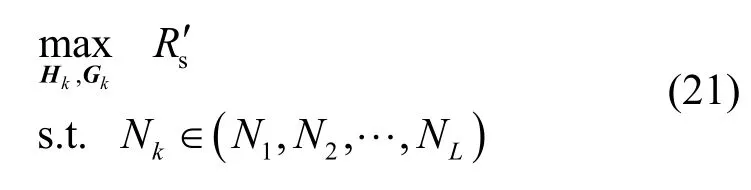
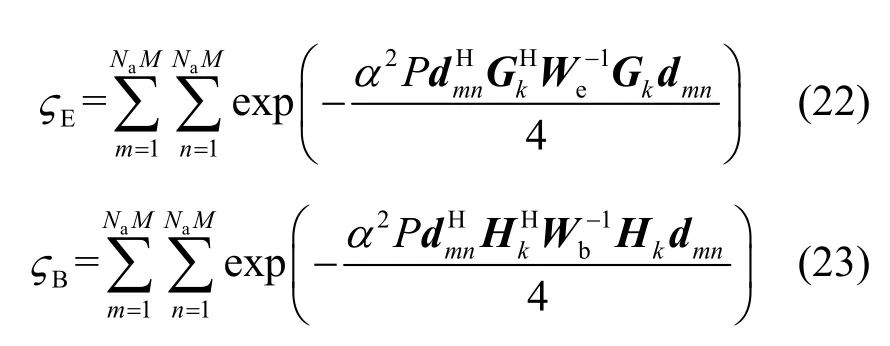
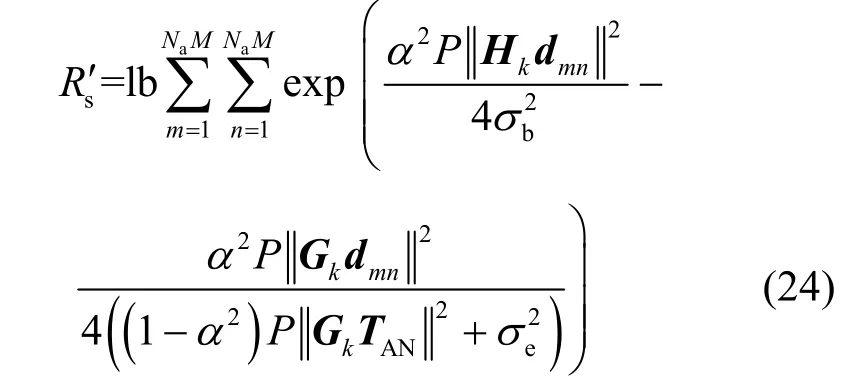
其中，Hk、Gk与所选的TAS 模式有关。通常最大SR 可以通过穷举搜索获得，并使发射端获得选择为最佳TAS 模式的最大SR 性能。

3.3 改进的优化搜索算法

COR 算法只是对SR 做了近似，但是其仍然需要遍历所有的天线组合，当天线数较大时，复杂度较高。针对这个问题，本文基于矩阵Frobenius 范数的相容性，提出一种ICOR 算法，将COR 算法中先组合再遍历的计算顺序变为先遍历再组合，即先遍历所有天线，再按照所需进行组合，这样能够避免遍历天线的所有组合。

在式(24)中，dmn与信道系数矩阵不相关，M=4可以作为常量归一化。同时，TAN是归一化AN 矩阵，将归一量省略，得到简化式，如式(25)所示。

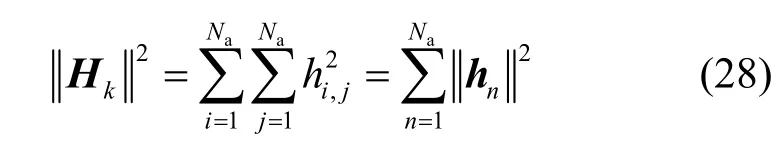
算法1ICOR 算法的求解过程

3.4 算法复杂度分析

基于COR 的天线选择算法的基本思想是获得TAS 模式的每个SR 并搜索(k∈{1,2,…,L})以找到最佳SR。算法的整体复杂度为，在低阶符号调制时，其比文献[18]中基于Max-SR的算法复杂度更低，但是这2 种算法都需要遍历天线组合，随发射天线数的增加而呈指数级增长。而ICOR 算法的整体复杂度包含列范数差值计算 O(Nt)和排序过程 O(lbNt)，与文献[18]中基于SLNR 算法的最低复杂度O(NtlbNt)相当。相比于最大COR 算法和Max-SR 算法，ICOR 算法的复杂度只取决于发射总天线的个数，且有着更好的稳健性和更低的复杂度。

4 功率分配与误码率

4.1 功率分配

选择信道后，式(24)便成了关于功率分配因子的函数。根据截断速率式对功率分配因子的最优值进行求解，此处认为总功率保持不变，则保密速率是关于功率分配因子的连续函数。对保密速率进行一阶求导得到极值解，将所对应的极值与边界点的值作比较，求得最大值，并给出最大值对应的分配因子。

令

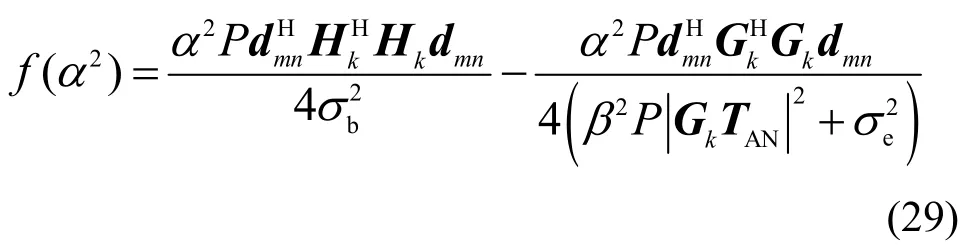
将式(30)写成二元一次方程的形式为

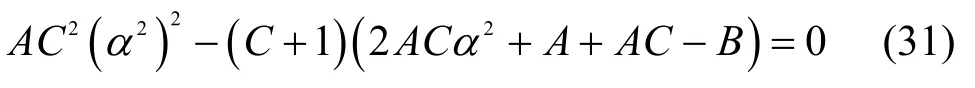
通过对式(30)的分析可知，f(α2)的Δ=4ABC2·(C+1)＞ 0是关于α2的凸函数，同时lb ∑exp能够保持凸函数的性质[19]。另外，根据计算结果可以发现函数f(α2)最大值不在α2=0和α2=1处取到。然后，根据求根式得到极值解，函数f(α2)极值解的表达式为式(32)，所求得的解为最大化截断速率的最优功率分配因子，是最大化保密速率的次优解。

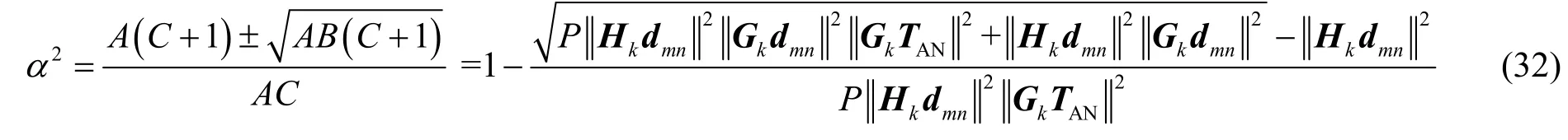
4.2 误码率

经过天线选择算法和最优功率分配后，接收端可以根据反馈的信道状态信息检测出原信号。由于精确的误比特率难以获得，本文通过推导成对差错概率来获得平均误比特率的上界。

SM 信号经过MLD 算法检测后，采用联合上界的方法，则误比特率可以表示为[26]

其中，Pr(xmi→xkj)表示将激活天线m、APM 符号si组合错判成激活天线n、APM 符号sj组合的成对差错概率，对于Bob 而言，其可以表示为均值为0、方差为的高斯随机变量，因此，有

其中，N(i,j)是每一个信道的汉明距离。在瑞利信道下，类似文献[27]相关的推导，得到Bob 的接收误比特率为

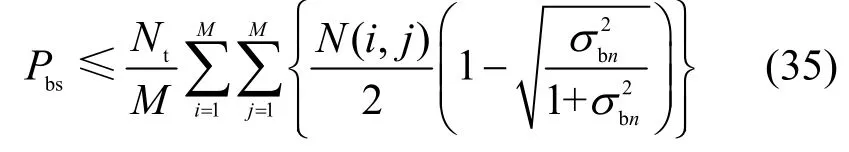
对于Eve，可以将人工噪声表达为信道噪声的一部分，从而Eve 接收误比特率为

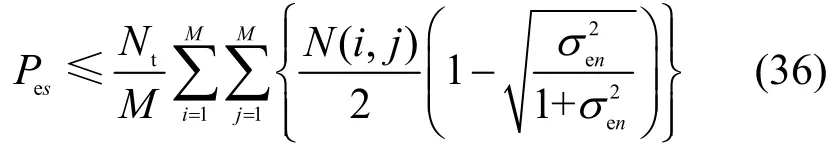
考虑到实际情况下，Eve 端无法得到反馈的CSI，因此，即使窃听者知道激活天线的序号，也无法对空间比特信息进行正确的估计。当系统发送二进制比特信息流时，窃听者有50%的概率正确估计出比特信息，因此空间比特信息的错误比特数可以表示为远大于调制比特的错误比特数。对于Eve来说，最终的误比特率可以近似表示为[28]

5 仿真结果

不同的TAS 策略将带来不一样的性能，同时具有不同的计算复杂度。本节在频率平稳的平坦衰落环境下，利用Matlab 平台进行仿真，分析和比较本文提出的ICOR 方法与文献[18]提出的SLNR 算法和Max-SR 算法在不同的信噪比和功率分配因子下的性能。同时，信道统一采用瑞利信道，其中，H和G 的元素是从具有单位方差的复数高斯分布中提取出来的，信道噪声的方差均归一化为0 dB，信噪比定义为。假设发射端总的天线数Nt=10，发射符号天线数分2 种情况讨论，分别为Na= 4和Na=8M= 8。Bob 和Eve 接收端天线都设置为Nb=Ne=2。另外，APM 采用二阶QPSK 调制，即M=4 。在未考虑功率因子的情况下，功率因子2α 都设置为式(32)中得到的最优功率因子。

功率因子分别为α2=0.75、α2=0.50和α2=0.25时，3 种不同TAS 方法对应的平均SR 性能与SNR的关系如图1 所示。通过将SLNR 算法和Max-SR算法与本文提出的ICOR 算法进行比较可以看出，本文提出的ICOR 算法在所有SNR 区域中都可以实现比文献[18]方法更高的平均SR，这表明其性能优于SLNR 算法和Max-SR 算法。此外，当SNR 逐渐增加时，所有TAS 算法的平均SR 都收敛于常数，这也意味着提高SNR 不会无限期地增加平均SR，因为有限的字符输入无法像高斯输入那样使互信息量达到信道容量。同样，随着SNR 逐渐增加，在α2=0.75的情况下，平均SR 明显优于α2=0.50和

2=0.25 α这2 种情况，这意味着在存在AN 辅助优化SR 的情况下，功率分配给AN 能够十分明显地增加SR。但是，单纯将功率多分配给AN，少分配给发射符号并不能更好地提升SR，需要在具体的SNR 区域进行讨论。通过对功率分配进行优化能够进一步提升系统的SR 性能，并且根据解析表达式的结果能够得到应该分配多少的功率给发射符号以及分配多少的功率选择发射人工噪声。

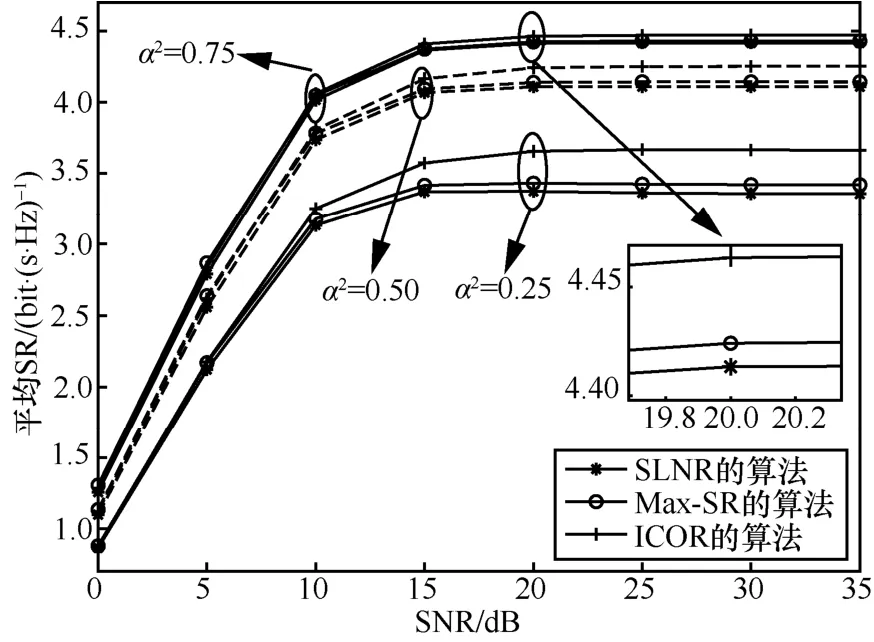
图1 3 种不同TAS 方法平均SR 与SNR 的关系

图2 讨论了当SNR 分别为5 dB、15 dB和25 dB时，不同功率分配因子对平均SR 性能的影响。当处于较低的SNR 区域时，能够取得最大保密速率的功率因子较大，因为较小的发射功率分配给AN，无法对Eve 端产生很大的干扰。当SNR 较高时，发射功率较大，但是有限符号输入下，分配给发射符号更多的功率并不能带来更多的SR 增益，所以此时分配多余的功率发射AN能够有效地干扰Eve，从而提升SR。此时，最优的功率分配因子会出现在0.5 附近。通过比较经过ICOR 算法筛选之后的天线和随机选择的天线这2 种情况可以看出，经过ICOR 算法得到的SR 性能相较于随机天线的组合有较大的提升，尤其是在低SNR 区域。随着SNR的增大，SR 也趋于稳定，所以经过COR 算法选择后的SR 增益相对减小。

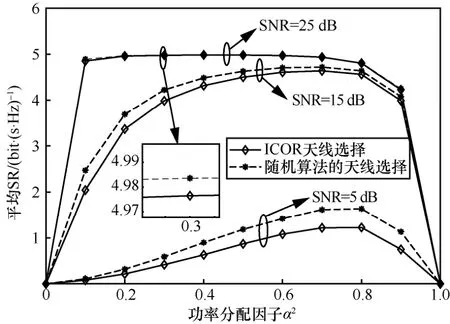
图2 不同SNR下的平均SR与功率分配因子2α 的关系

图3 显示了SLNR 算法和Max-SR 算法的平均BER 与SNR 的关系曲线，并与本文提出的ICOR算法进行比较。通过使用与图2 相同的系统参数设置，进一步分析3 种TAS 方法对平均BER 的影响。由于Eve 没有获得从Alice 发送的有关空间和星座比特位的信息，因此她只能对本地的每个二进制位进行随机猜测。因此，Eve 获得的BER 等效于式(37)的结果。显然，随着SNR 的逐渐提高，这3 种方法的平均BER 在低SNR 区域几乎相同，但是在高SNR 区域，本文提出的ICOR 算法的平均BER 性能优于SLNR 算法和Max-SR 算法。这意味着，本文提出的ICOR算法可以通过适当地提高SNR来改善SM 系统的BER 性能。

图4 分析了不同发射天线数（Na=4 和Na= 8）下平均BER 与SNR 的关系，并给出了Eve 在获得反馈信道状态信息和反馈信道状态信息情况未知的BER。从图4 中可以看出，在发射总天线不变的情况下，提高发射符号的天线数能够有效提升Bob 和Eve 端的BER 性能，特别是在SNR 较高的区域。Eve 在已知CSI 的情况下，能够比未知CSI 的情况下具有更好的BER 性能，也意味着，人工噪声对Eve 的影响有所减小。特别是在SNR较高的区域，Eve 虽然受到人工噪声的干扰，但是人工噪声只考虑了不影响合法接收者，所以Eve 仍然能够获得比未知CSI 情况下更多的BER性能。而同时处于未知CSI 的情况下，更少的发射天线意味着更少的猜测比特位，所以Eve 的检测错误概率也越小。

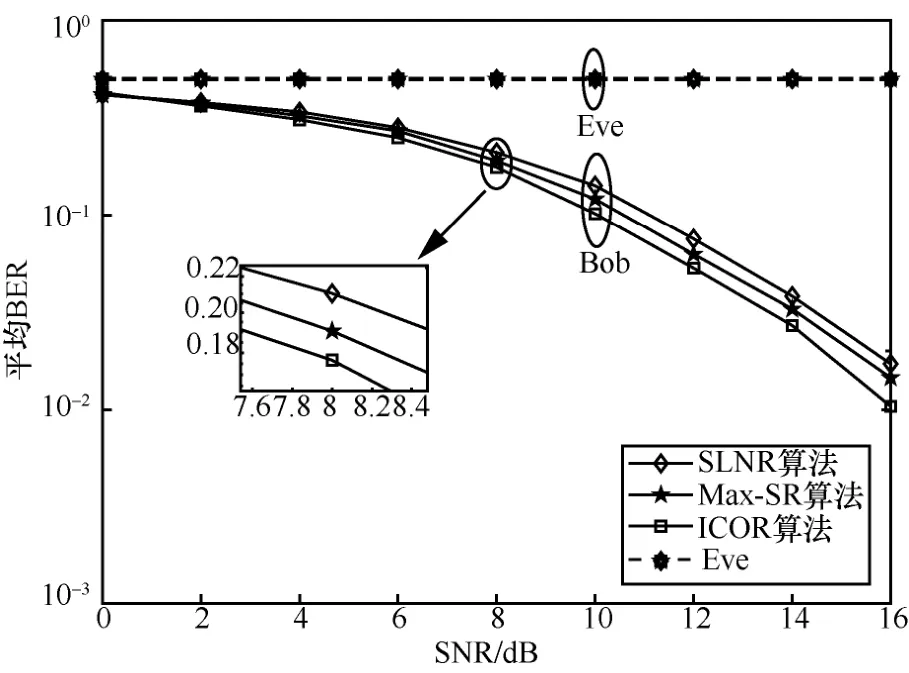
图3 3种不同TAS方法平均BER与SNR关系

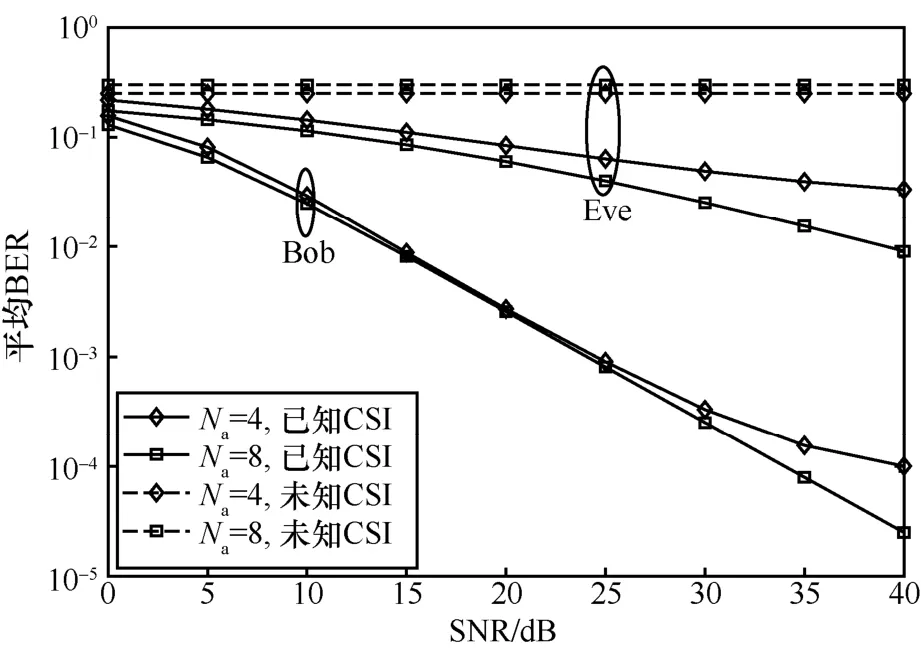
图4 不同发射天线数的平均BER 与SNR 的关系

图5 比较了 Max-SR 算法与本文提出的ICOR 算法及经过搜索算法优化之后的ICOR 的计算复杂度，SLNR 算法的复杂度与ICOR 算法一致。当发射天线数固定为Na=4 根时，随着发射天线总数的增加，需要考虑组合次数的Max-SR 算法和COR 算法的计算复杂度呈指数级增长，相比之下，只需要考虑发射天线总数的ICOR 的复杂度增长有限。当发射天线数提升到Na=8时，Max-SR 和COR 的计算复杂度有更大幅度的提升，并且随着发射天线总数的增加，计算复杂度增长的幅度还在增大。相比之下，ICOR 算法的复杂度不会随着发射天线数Na的变化而变化。对比分析3 种TAS 方法的计算复杂度，经过优化搜索算法改进的ICOR 极大地降低了发射天线选择的复杂度。

图5 不同TAS 下不同发射天线数的计算复杂度与发射端天线总数的关系

6 结束语

本文针对有限符号输入下安全SM 系统中传统算法保密速率性能低和算法复杂度高的问题，提出一种基于COR 的天线选择算法。该算法把COR 作为SR 的近似表达，将最大化SR 的问题转化为优化COR 的问题。基于接收端的条件概率密度函数，推导出COR 的闭式表达式，并根据对COR 表达式的分析，提出低复杂度的ICOR 算法。该算法通过将矩阵范数按列展开，得到合法接收者信道列范数和非法窃听者信道列范数。然后，根据两者信道列范数的差值进行排序筛选出使差值最大的天线组合，从而通过选择的最优天线组合最大化COR。另外，将AN 技术应用到安全SM 系统中，在给窃听者发射额外干扰的同时不影响合法接收者，从而进一步提升系统的SR 性能。仿真结果表明，本文所提出的ICOR 算法在安全的SM 系统中可以实现更高的SR 和更低的BER，其SR 性能优于SLNR 算法和Max-SR 算法。同时，ICOR 算法极大地降低了最大化COR 算法的计算复杂度。本文所提的ICOR 算法是基于截断速率的功率分配因子的次优解，如何直接求解最大化保密速率本身的最优解将是下一步工作的重点。