城市生活垃圾处理设施多目标优化选址研究
朱娇娇, 陈 荔, 吴建俊
(上海理工大学 管理学院, 上海 200093)
随着城镇化进程加快,城市生活垃圾排放量日益增加,对垃圾中转站、填埋场和焚烧厂等城市生活垃圾处理设施的需求不断增多。目前,在“无废城市”的创新、协调、 绿色、开放、共享的新发展理念下,如何管理城市生活垃圾成为居民和政府关注的重点,其选址问题也得到了学术界的高度关注[1]。文中所指的城市生活垃圾处理设施选址是一种半厌恶型设施选址。从社区居民的角度考虑,设施点应建立在远郊地区;从收运成本的角度考虑,设施点应建立在市中心和人口聚集地。同时城市生活垃圾处理设施选址也属于公共设施选址,涉及到政府、居民等相关者的利益,不仅要符合公共设施的选址要求,还要让更多的人享受社会福利[2]。因此,政府管理部门应综合考虑总成本和环境负效用等因素来规划建设城市生活垃圾处理设施。
目前,国内外很多学者对废弃物处理设施选址问题进行了深入研究。Erkut E等[3]以希腊马其顿地区的都市固体废物管理设施为选址对象建立了多目标优化模型,考虑了总成本、总负效用和个体效用等目标;Brimberg J等[4]提出一种多目标模型,并通过加权法将多目标问题转换为单目标问题,考虑了总成本和未被服务的需求点等目标;Eiselt H.A.等[5]以智利某垃圾填埋场和中转站选址为背景,建立成本最小化和污染最小化的双目标混合整数规划模型,同时确定了将要建立的垃圾填埋场的规模;Silva S等[6]将GIS技术与优化技术相结合,提出一种以沼气厂为研究对象的多目标优化模型,考虑了初始投资和运维成本、运输成本和社会负效用三个目标;Harijani A等[7]综合考虑废弃物处理设施的类型、设施容量水平以及所处的位置等因素,提出了一种多周期多目标的优化模型。
近年来,国内相关的研究多数局限于以建立垃圾中转站、卫生填埋场和焚烧厂等的总成本和负效应为目标建立优化模型。贾传兴等[8]为选出垃圾中转站的最优组合, 考虑了城市垃圾收运系统的特点,并以城市垃圾中转站为研究目标分别建立集合覆盖模型和城市垃圾收运系统费用现值最小模型。何波等[9]考虑了系统成本和社会负效用两个目标,以废弃物处理站为研究对象建立多目标优化选址模型,并在求解质量上与约束法进行比较;王海燕等[10]基于扩散距离的负效应测度方法,以带中转设施的城市废弃物三层物流网络为研究对象,建立以成本和人均负效应最小化为目标的中转站选址问题的优化模型,并根据问题特征,设计一个模拟退火算法与贪心算法相结合的混合算法(HSA)进行求解; 夏明燕[11]针对城市固体废弃物处理设施的选址和容量问题,建立多目标优化模型,并采用遗传算法和PRO模型法进行求解;张沁莞等[12]提出以深埋式垃圾桶作为选址研究对象,建立以建设和运维成本、运输成本和用户负效用最小化为目标的多目标优化模型,用于解决传统小型垃圾收运设施垃圾暴露、运输效率不高等问题。综合国内外文献,多数是从城市固体废弃物角度建立优化模型,而关于城市生活垃圾处理设施的文献较为匮乏。
城市固体废弃物设施的选址模型能够为城市生活垃圾处理设施的选址模型提供参考,但不能与之完全匹配。文中提出以城市生活垃圾处理设施点到需求点的产生量和距离值的乘积之和最小以及需求点处的生活垃圾未得到处理时的环境负效用最小为目标建立优化模型,综合考虑了经济和社会效益。此外,根据模型自身的特点,文中设计免疫优化算法对其进行求解,证明了模型的可行性和算法的有效性,并以上海市的城市生活垃圾处理设施为选址目标,为相关管理部门在城市生活垃圾管理问题上提供理论参考。
1 城市生活垃圾处理设施选址模型
1.1 问题描述与模型假设
上海市某区域的城市生活垃圾处理设施为例,以每个生活垃圾处理设施所供给的需求点数量、被选择的生活垃圾处理设施量、需求点的垃圾产生量作为约束条件建立以实现整个垃圾回收选址系统:城市生活垃圾处理设施点到需求点的产生量和距离值的乘积之和最小以及需求点处的生活垃圾未得到处理时的环境负效用最小为目标建立双目标优化模型;然后,设计一种群体搜索的免疫优化算法对其求解。
为便于建立选址模型,给出如下假设:①城市生活垃圾处理设施能够容纳的生活垃圾由其收集范围内垃圾的产生量来决定,并且总容量总是可以满足需求点的总需求;②城市生活垃圾处理设施只能在需求点中建立;③不考虑城市生活垃圾处理设施到终端处理点的运输费用;④终端处理点对需求点人口不产生直接负效用;⑤一个需求点产生的所有生活垃圾仅由一个城市生活垃圾处理设施来集中收运。
1.2 符号说明
文中所用参数及决策变量,其含义如下:
I:所有需求点的序号集合,i∈I,I={1,2,...,m};
S:城市生活垃圾处理设施候选点到需求点的上限距离;
Ri:到需求点i的距离小于S的城市生活垃圾处理设施候选点的集合,Ri={1,2,...,n},i∈I,Ri⊆I;
βi:需求点i处的需求量;
dij:需求点i到离它最近的城市生活垃圾处理设施j的距离,j∈Ri;
N:规定被选定的城市生活垃圾处理设施的数量;
r:受影响的圆形区域半径;
zij:城市生活垃圾处理设施j对需求点i产生的负效用;
c:单个城市生活垃圾处理设施j对个体影响所造成的环境补偿成本;
pri:位于城市生活垃圾处理设施j所影响的人口数量。
1.3 模型构建
(1)
(2)
s.t
(3)
(4)
uij≤yj,i∈I,j∈Ri
(5)
uij,yj∈{0,1},i∈I,j∈Ri
(6)
dij≤S
(7)
目标函数式(1)为各城市生活垃圾处理设施候选点到需求点的需求量和距离值的乘积之和最小;目标函数式(2)为需求点处的生活垃圾未得到处理的环境负效用最小;约束条件式(3)为保证每一个需求点只能由一个城市生活垃圾处理设施提供垃圾收集服务;约束条件式(4)为被选定为城市生活垃圾处理设施的数量;约束条件式(5)为需求点的生活垃圾只能由被选定的城市生活垃圾处理设施的点来收集分类;约束条件式(6)为决策变量的取值范围;约束条件式(7)为保证需求点在城市生活垃圾处理设施范围内。
2 免疫算法
免疫系统是自适应生物系统之一,其功能是识别和消除异物。免疫算法(Immune Algorithm,IA)是一种受生物免疫系统启发,在免疫学理论基础上发展起来的一种新兴的智能计算方法,能够克服寻优过程中的“早熟”问题和快速收敛于全局最优解,并利用免疫系统的多样性抑制进化过程中的简并现象,保持了免疫系统的多样性,对组合优化问题具有良好的性能。免疫优化算法的基本思想为:随机产生N个个体并从中提取m个个体构成初始种群,对上述种群中的各个个体进行解的多样性评价,按照期望繁殖率P进行降序排列,并取前N个个体构成父代群体,同时取前m个个体存入记忆库;采用单点交叉法和实数变异法分别进行交叉和变异操作,抑制、消除相同和相似的高浓度个体并且采取精英保留策略,如此重复上述迭代过程,直至得到全局最优解[13]。
文中运用免疫优化算法对上述城市生活垃圾处理设施选址模型(1)—(7)进行求解,现将算法中提及的初始抗体群的产生、期望繁殖率的计算方法和免疫操作等关键步骤做如下具体的说明。
2.1 初始抗体群的产生
随机产生N个个体,若记忆库为非空,则从记忆库中选取m个个体作为初始抗体群,其中m为记忆库中个体的数量;若记忆库为空,则可以在可行解空间随机产生初始抗体群,采用简单编码的方式[14]。若城市生活垃圾处理设施的数量为n,则一个长度为n的抗体对应于一个选址方案,每个抗体即是一组被选为城市生活垃圾处理设施的需求点序号。以表1中的数据为例进行说明,1-30表示需求点的序号,从中选取5个作为城市生活垃圾处理设施点,则抗体[6 16 26 29 30]即为一个可行解,表示序号6,16,26,29,30被选为垃圾处理设施点。
2.2 期望繁殖率计算方法
根据个体的期望繁殖率P进行评价,则该抗体的评价标准为:
(8)
(9)
(10)
(11)
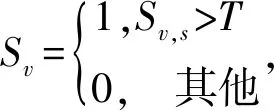
2.3 免疫操作
免疫操作是指抗体产生的三个阶段,分别为选择、交叉和变异操作。其中,选择操作是指按照个体的适应度值采用轮盘赌法选择个体,个体被选择的概率即为式(8)计算的期望繁殖率P;交叉操作和变异操作分别是指采用实数交叉法和实数变异法进行交叉和变异。
算法步骤如下:
step1:分析问题。分析文中所研究模型及其可行解的特性,并设计合适的表达形式;
step2:产生初始抗体群。如果记忆库非空,则初始抗体群从记忆库中生成;反之,在可行解空间随机产生N个个体并从中提取m个个体构成初始群体;
step3:对初始抗体群的每个个体根据期望繁殖率P进行评价;
step4:构成父代群体。根据抗体的期望繁殖率P提取前N个个体形成父代群体和前m个个体存入记忆库;
step5:判断是否满足算法结束条件,是则结束并输出优化结果;反之,继续step6;
step6:新群体的产生。根据step4的结果对抗体进行免疫操作得到新群体,和记忆库中的抗体构成新一代群体;
step7:转step3。
2.4 算法流程图
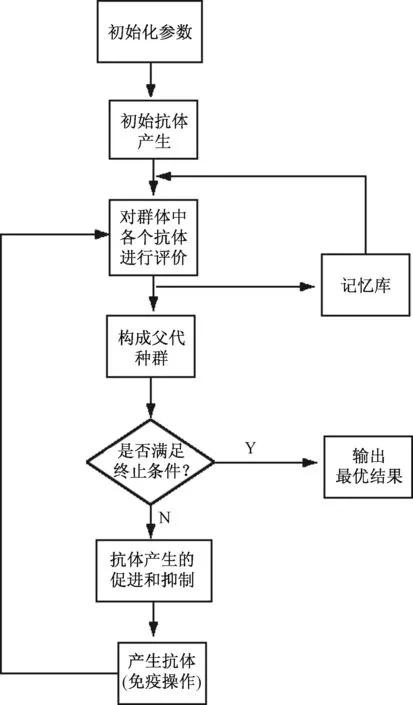
图1 免疫算法流程图
3 算例仿真
3.1 算例说明
根据实地调研,选取上海市30个生活垃圾需求点作为研究主体,每个需求点的坐标及生活垃圾产生量见表1,其中表中所提及的垃圾产生量是经过规范化处理后的数值,不代表实际值。各城市生活垃圾需求点的位置如图2所示,并从中选择5个作为城市生活垃圾处理设施点。算例中的相关参数见表2。
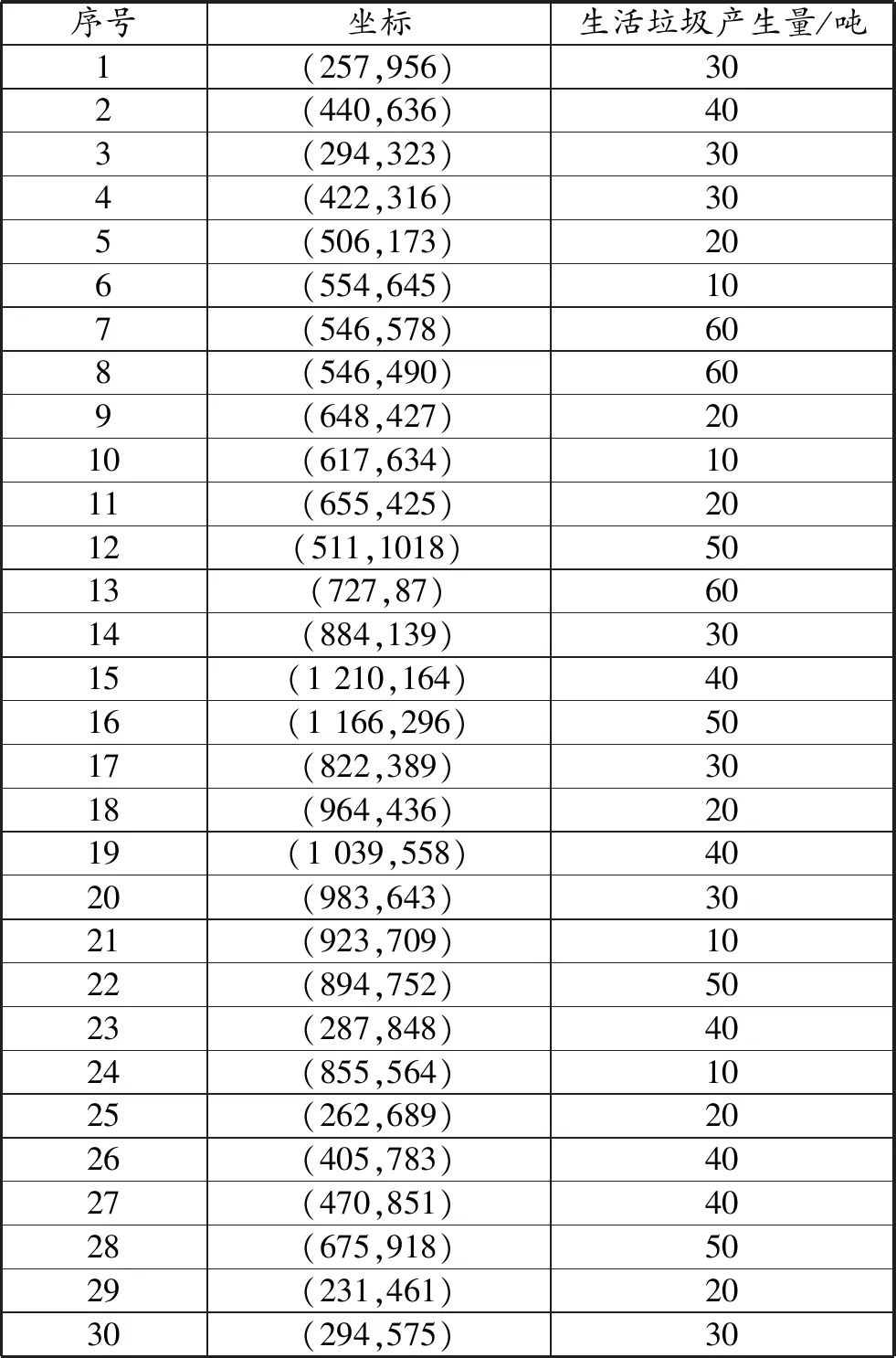
表1 城市生活垃圾的产生点坐标及其产生量
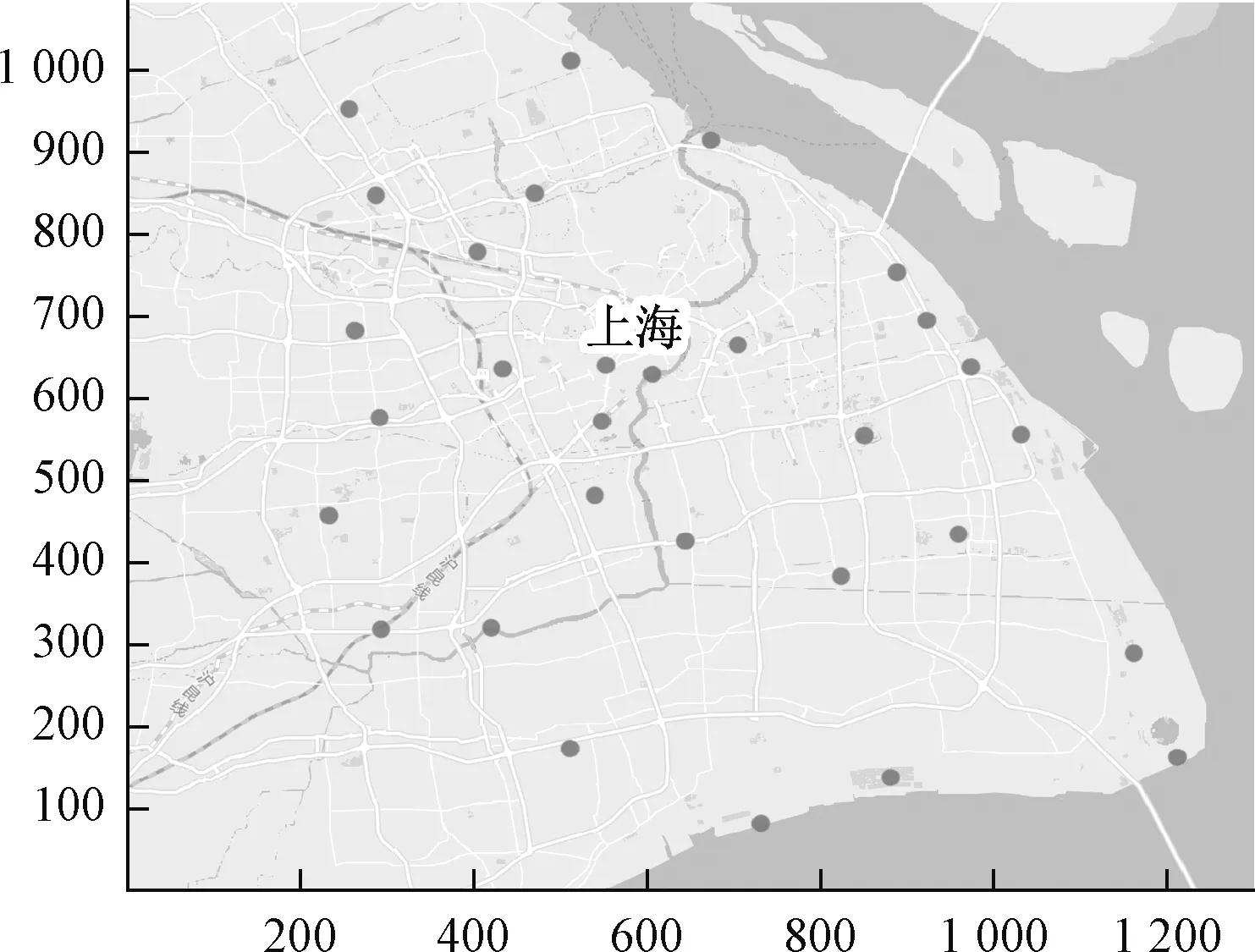
图2 上海市部分区域地图
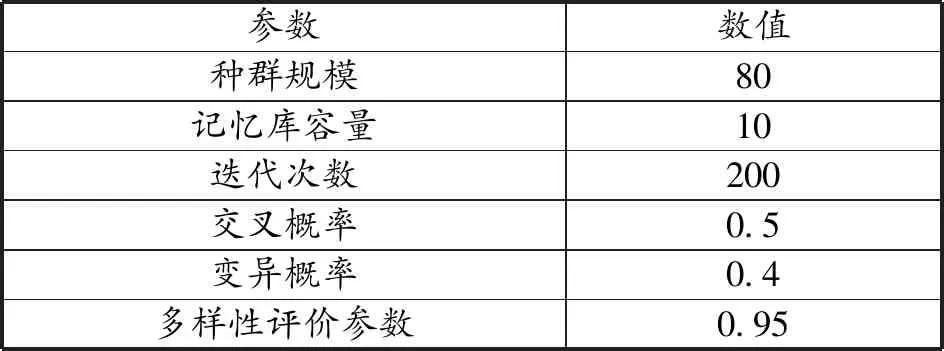
表2 算例相关参数
3.2 算例求解
实验所用硬件环境为IntelRCore(TM) i5-8265UCPU@1.60 GHz, 8.0 GB内存,64位 Windows10 操作系统,编程工具为Matlab2016b。
免疫优化算法经过200次迭代后得到的平均适应度值为7.14×105,最优适应度值为6.32×105,如图3所示;图4 给出了免疫优化算法的最优选址方案,其中正方形表示被选为城市生活垃圾处理设施点,圆形表示为设施点之外的城市生活垃圾需求点;连线表示该处的需求点产生的生活垃圾由此设施点收集。模型计算所得结果为[12 9 27 19 5],表明城市生活垃圾处理设施最优的选址序号为12,9,27,19,5。
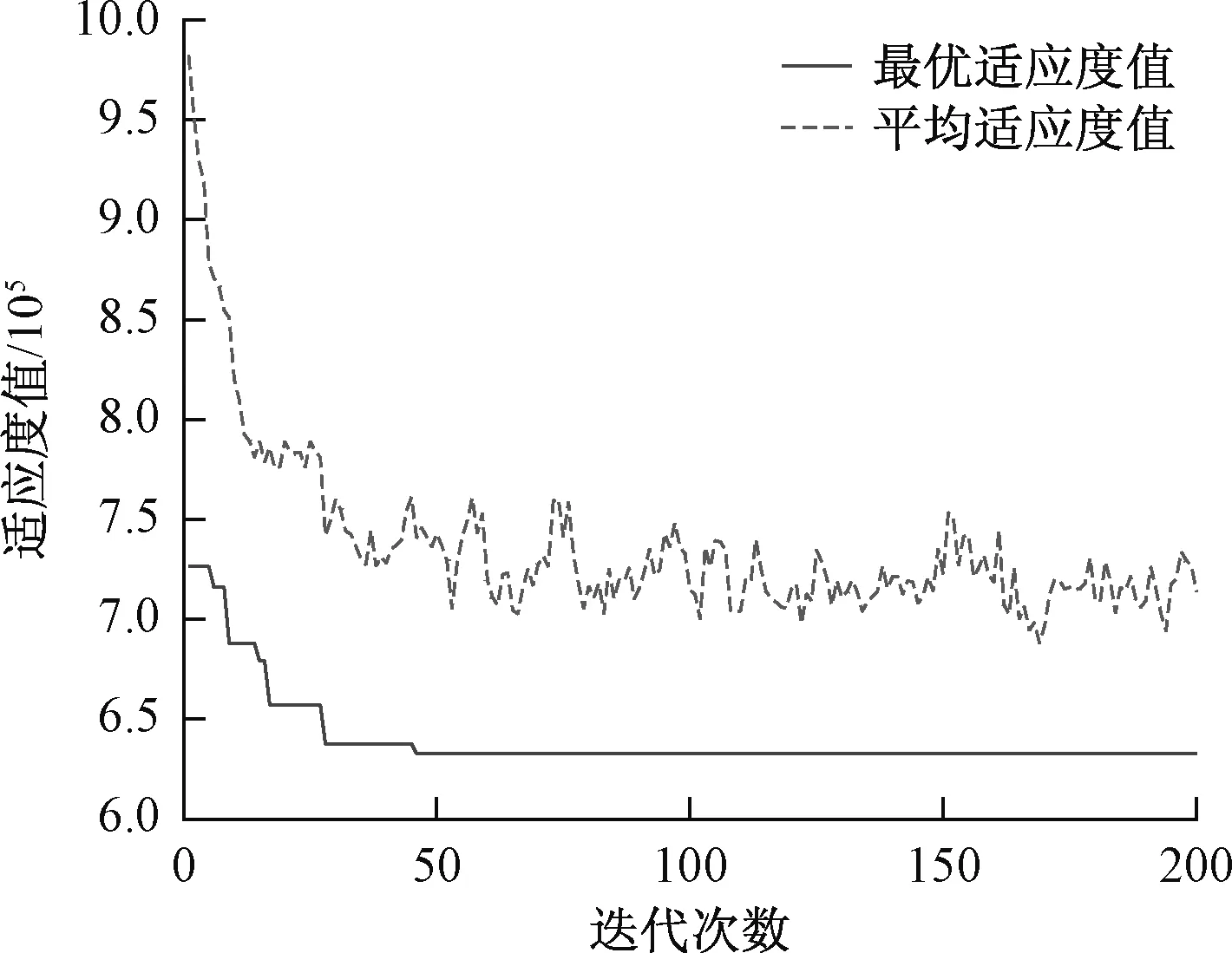
图3 免疫优化算法收敛曲线
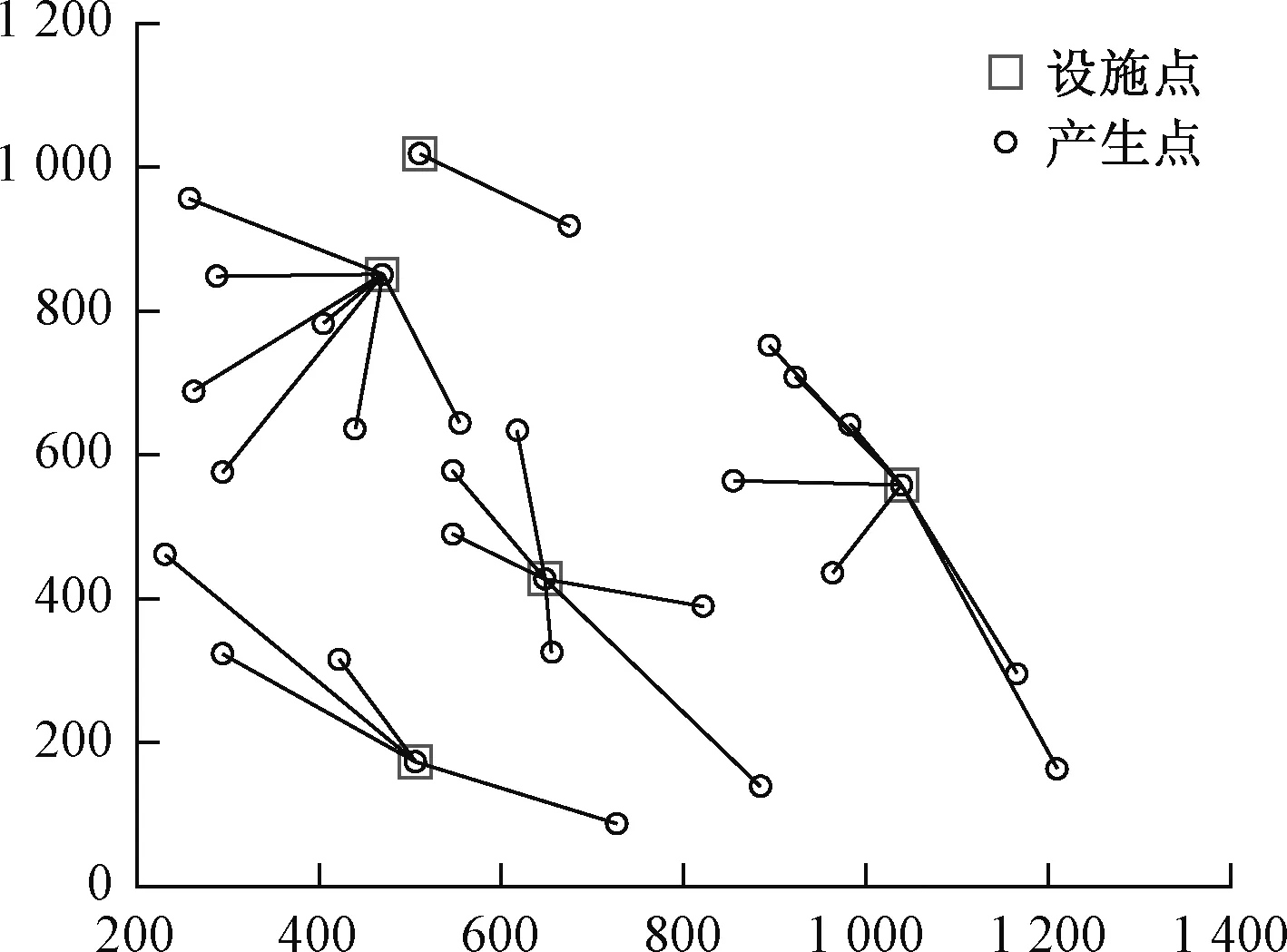
图4 城市生活垃圾处理设施选址方案
4 结束语
针对城市生活垃圾收运系统的特点和满足距离上限的情况下,考虑各城市生活垃圾处理设施点到需求点的产生量和距离值的乘积之和最小以及需求点处的生活垃圾未得到处理时的环境负效用最小为目标建立优化模型。该模型能够解决“在哪里设置城市生活垃圾处理设施”和“最优规划生活垃圾收运路线”两个问题,并设计免疫优化算法对设施进行优化选址。最后通过算例,证明了模型的有效性和可行性,为相关管理部门建立城市生活垃圾处理设施提供了理论支持,具有重要的应用价值。

