使用Gibbs最小能法分析三氯氢硅的还原过程

司文学 汤传斌

(中国恩菲工程技术有限公司， 北京 100038)

0 前言

西门子法生产多晶硅的过程中，高纯的氢气和三氯氢硅作为原料在CVD还原炉中发生一系列复杂的化学反应。到目前为止，相关技术人员对其反应过程的研究主要分为以下两个方面：一是先拟合一系列的化学反应关系式，然后根据各个反应方程的化学平衡常数计算反应产物中各个成分的量[1-3]，但是该方法在很大程度上受所拟合的化学反应关系式影响，很难适应不同条件下的三氯氢硅的还原过程；二是研究CVD还原炉内热场、流场的分布[4-7]，主要用来设计进、出料口的形式和位置以及硅棒的布置形式，以达到热场和流场分布均匀，并减少热损失。但是这两种方法有很大的局限性，有些问题并没有从理论上加以解释，如为什么一定要把还原尾气中的微量氯化氢分离干净、为什么一定要使用高纯的三氯氢硅进入到还原炉中等。因此，本文从热力学的角度使用Gibbs最小能法对这些问题加以说明，以期为相关的科研技术人员提供一些方向。

1 Gibbs模型方程的建立和求解

根据热力学原理，反应系统总Gibbs自由能在平衡时取得极小的这个判据可以确定平衡时系统内各个物质的含量，这种方法并不涉及具体的化学反应方程式，从而避开了系统的反应机理部分，而且这是一种普遍适用的算法，并且不需要限制入口的物质种类，只需要给定入口的各种原子总数，这种方法就是Gibbs最小能法。

1.1 模型方程的建立

Gibbs最小能法是一个典型的在一定约束条件下求极值的数学问题，可以通过增加拉格朗日算子并通过迭代求最小值[8-12]。

在已知ni的情况下，求解式(1)就可以得到拉格朗日算子λ：

(1)

其中：

(2)

(3)

(4)

物质含量ni的迭代计算：

(5)

式中：n——各种物质的量，mol；

λ——拉格朗日算子；

A——各种原子总数，mol；

aik——组分i中原子k的数量；

GΘ——标准态吉布斯自由能，J/mol；

R——气体常数，J/(mol·K)；

T——温度，K；

P——系统总压(绝)，Pa；

y——各种物质的摩尔分数。

1.2 模型求解过程

迭代求解Gibbs最小能时体系中各个组分含量的步骤[8-9]如下：

1)给定系统的稳定T和总压P、系统中的物质种类数N、各种物质中的原子数量a、系统中各种原子种类数M、各种原子总数A。

2)给出一组化学平衡时体系内各个物质含量初值n0。

3)将n0代入方程(1)～(4)，可以得到一组拉格郎日算子λ和u。

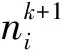
(6)

(7)

6)对比n0和n1，判断n1是否满足迭代要求。首先按式(8)计算每种物质含量的相对误差εi，若计算的每个εi均小于迭代允许误差，则数组n1就是化学反应达到平衡时体系中各种物质的含量，计算结束；否则令n0=n1，返回步骤3)计算新的拉格郎日算子λ，直到n1满足迭代误差的要求。

(8)

2 Gibbs方程的模拟计算

对某多晶硅生产企业的CVD还原炉建模，设定原料流量为10 000 mol，并按氢气和三氯氢硅的配比为3、反应压力0.5 MPa(表压)进行模拟计算。

2.1 物质种类及元素组成

为了准确预测还原炉内的反应产物的物质种类及物质含量，将所有可能存在的物质都添加到Gibbs最小能的计算程序中，共有15种物质，每种物质的标准态吉布斯能GΘ及元素组成a的值见表1。

2.2 模型模拟验证

由于CVD还原炉生产多晶硅的过程非常复杂，为了方便研究其机理过程和影响因素，将其反应过程简化为以下三个过程：

1)体系内的物质在1 050 ℃的硅棒表面发生化学反应，生成的硅沉积在硅棒表面起到分离作用，而气体物质扩散到气相空间。

2)扩散到气相空间的物质继续发生化学反应，生成的固体硅中有一部分沉降在地盘上，一部分随气体流动过程中与硅棒表面接触后被吸附在硅棒表面，剩余硅随气流流出反应器并被过滤。在这个过程中，凡是没有沉积在硅棒表面的硅统称为无定形硅。

3)从还原炉出来的约800 ℃的高温气体继续被冷却到200 ℃后排出还原反应系统。在冷却过程中系统温度发生了变化，体系内的各种物质仍然会继续发生反应。

对上述三个过程进行模拟计算，结果见表2。

表1 物质种类及元素组成

表2 硅棒表面反应后的物质组成

由表2可知，物质3、4、5、7、9、10的体积含量都很小，可以忽略不计；而物质6和11的体积含量与技术人员关注的物质1、2、8、12、13、14、15的体积含量相比不能忽略。但在以往，由于对反应机理认识不够充分，物质6和11都被忽略了。根据表2，可以进一步得到这3个过程分别生成的硅量(Si1、Si2、Si3)，其结果见表3。

表3 简化还原过程的硅产量 mol

1)SiHCl3的一次转化率。据表3可以得到SiHCl3的一次转化率为226.02/2 500=9.04%，该模拟值与某多晶硅生产企业统计的三氯氢硅10%的一次转化率相接近。

2)SiCl4的产率。从表2可以得到SiCl4的产量是835.38 mol，其与硅产量的比值是(835.38×169.89)/(226.02×28.09)=22.35，该模拟值与某多晶硅生产企业统计的比值20接近。

3)Si2Cl6的产率。从表2中可以得到Si2Cl6的产量是1.33 mol，其与硅产量的比值是：(1.33×268.88)/(226.02×28.09)=0.056，该模拟值高于某多晶硅生产企业统计的比值0.035～0.04，这是由于实际生产中Si2Cl6是由高沸物精馏后得到的，损耗较大造成实际统计值偏小。

4)还原尾气成分。其模拟计算结果与实际检测结果对比见表4，其中HCl的误差最大，这很大可能是由于检测取样过程中氯硅烷发生分解生成了HCl，对检测结果造成影响。

综上所述，通过对主要因素的比较分析，可以证明本文所采用的Gibbs能最小法和对三氯氢硅还原过程机理的简化是可行的。

表4 还原尾气成分(摩尔含量)模拟结果与实际检测值的对比

3 利用Gibbs最小能法分析影响多晶硅产量的因素

3.1 气相温度的影响

在保持氢气和三氯氢硅的配比为3、总进料量为10 000 mol的前提下，改变过程2的气相温度，模拟计算关键物质三氯氢硅(TCS)、四氯化硅(STC)、二氯二氢硅(DCS)以及总硅的产量，找到最佳气相温度，其计算结果如图1所示。

由图1可知，当气相温度为620 ℃时，最终得到的多晶硅产量和STC产量达到最大， TCS产量和DCS产量最小；DCS产量随气相温度的变化影响较小。

3.2 回收氢气纯度的影响

在还原尾气中的氯硅烷和硅分离后，将剩余的氢气和氯化氢的混合物循环回还原炉继续反应(即过程3中硅分离后的气体作为原料直接循环回CVD还原炉中)，结果见表5。

图1 气相温度对产物产量的影响

从表5种可以看出，若是只将还原尾气中的氯硅烷分离后，而不将中微量的HCl分离就将回收氢气循环进入还原炉，反应后的产物以H2和TCS为主，而且几乎没有新硅的产生，同时进入还原炉中的STC和DCS的体积含量都将减少。这就说明还原尾气必须经过处理净化后才能循环使用。

表5 回收氢气的纯度对产物产量的影响

3.3 原料中DCS含量的影响

从前述的模拟计算结果可以看出，气相空间产生的硅量Si2占到硅总量的较大比例。保持过程2的气相温度为800 ℃，在原料中增加DCS的同时等量减少原料中的TCS，模拟计算结果如图2所示。

由图2(a)可知，当原料中的DCS含量达到4%时，产物中的硅、DCS、TCS产量均达到最大值，然后开始下降，STC产量的变化趋势与之相反。图2(b)表明，随着原料中DCS含量的增加，直接在硅棒表面沉积的硅Si1量会增加，同时总硅产量会增大，并且在配比75∶4∶21时硅的总量达到最大；但随着DCS的量继续增大，除了Si1继续增加外，Si2和总硅量都逐渐减小。

3.4 原料中TCS含量的影响

保持过程2的气相温度为800 ℃，改变H2和TCS的原料配比，其主要产物产量的模拟计算结果如图3所示。

由图3可知，原料中TCS含量越高(即配比约小)，硅量、TCS和STC的产量越高，DCS的量变化不大；当配比约为12时，Si1=Si2；当配比大于12时，Si2逐渐占优势，达到一定程度时，Si1的量可以忽略；当配比小于12时，Si1逐渐占优势，但Si2的量不能忽略。虽然原料配比值减小后总硅量增加了，但Si2量也会增加，若是气体在还原炉内的湍流不充分、停留时间过短，Si2中在硅棒表面转化为多晶硅的比例就会降低，同时意味着有更多的无定形硅产生。

3.5 原料中STC含量的影响

保持过程2的气相温度为800 ℃，在原料中增加适量的STC并同量减少TCS，模拟计算结果见表6。从表6可以看出，随着原料中STC含量的增加，产物中硅量会减小，但DCS、TCS、STC的体积含量基本不变。

图2 DCS含量对最终产物产量的影响

图3 TCS含量对最终产物产量的影响

表6 原料中STC含量对产物产量的影响

4 结论

本文借助Gibbs自由能最小法对西门子法生产多晶硅中三氯氢硅的还原过程进行了分析，并得出以下结论：

1)本文所述的Gibbs自由能最小法以及将还原过程分为3个阶段的处理方式能够较好地反映实际装置的运行情况，模拟计算结果与生产统计数据和分析检测数据相吻合，说明所建模型的正确性。

2)在硅棒表面主要是TCS生成了Si，在气相空间主要是DCS生成了Si。原料配比(H2∶TCS)较高时，气相空间反应占优势，并且总硅的产量较低；原料配比较低时，硅棒表面反应占优势，并且总硅的产量较高。

3)气相空间的温度对总硅产量有较大影响。当原料配比是3∶1、气相空间温度是600 ℃时气相空间的硅产量和总硅产量达到最大值。

4)使用CVD法生产多晶硅的过程必须要有还原尾气的干法回收得到高纯的循环氢气，以及必须从干法冷凝料中提纯得到高纯的三氯氢硅，否则就不能实现还原尾气的分离回收和物料的循环利用。

5)提高原料配比中的TCS含量或在原料中添加适量的DCS,可以提高总硅产量。由于在原料中增加TCS或DCS的量，都会造成气相空间中硅的产量，需要改进还原炉结构，否则可能造成无定形硅产量的增加。

6)在原料中增加STC的含量，硅产量会降低，但还原尾气中的DCS、TCS、STC的体积含量变化很小。