长江经济带能源消费碳排放的多变量驱动因素研究——基于扩展STIRPAT模型

(南通师范高等专科学校(如皋校区),江苏 南通 226500)

2015年在巴黎召开的联合国气候变化大会上,我国政府在“国家自主贡献”中郑重承诺将于2030年左右使碳排放达到峰值,并使单位GDP碳排放下降60%—65%(以2005年为基期)。改革开放40年来,我国经济的快速发展是以能源消费的持续增长为基础的。2008年《BP世界能源统计年鉴》显示，2017年我国一次能源消费总量为44.77亿t标煤,占全球能源消费总量的23.2%和全球能源消费增长的33.6%,我国仍然是世界上最大的能源消费国;碳排放总量为92.326亿t,占世界碳排放总量的27.6%。因此，我国如果要实现巴黎大会的碳减排承诺,就必须走低碳发展道路以解决经济发展与碳排放同步增长的问题。长江经济带作为我国综合实力最强、战略支撑作用最大的区域之一,在实现碳减排的目标中起着至关重要的作用,因此研究该区域能源消费碳排放与经济增长之间的关系具有非常重要的作用。

能源消费碳排放与经济增长之间的关系一直是环境经济学领域的研究热点,且经典的研究分析工具之一是环境库兹涅茨曲线理论,该研究内容主要包括检验“环境库兹涅茨曲线”是否存在及其形态。从宏观层面看,28个OECD国家中部分国家碳排放与GDP的关系呈现倒“U”形,部分国家则呈现“U”形[1]。大多学者[2-5]认为我国碳排放量与经济发展之间基本存在倒“U”型曲线,目前处在拐点左侧。李国志[6]则认为我国1970—1989年不存在EKC曲线,1990—2015年存在倒“U”型曲线且拐点呈提前趋势;颜廷武等[7]认为我国农业碳排放强度与农业经济强度之间存在倒“N”型EKC关系和双拐点。我国各区域和各省份的碳排放与经济增长关系非常复杂,EKC曲线形态也多种多样,如沿海地区、新疆维吾尔自治区为“N”型[8,9],辽宁省为倒“N”型，江苏省、长三角地区等为倒“U”型[10,11]。另有学者认为，有些地方不存在EKC曲线,如陕西省[12]、长三角地区[13]、西部地区[14]。与之相关的是EKC曲线驱动因素研究,学者们借助LMDI[15,16]、VAR[17,18]、联立方程组[19,20]、ARDL[21]、Alasso[22]等模型研究了包括城镇化[13]、人口因素[23,24]、技术变革[18]、出口贸易[25,26]、环境规制[27]、产业结构[28,29]、公共支出[30]、金融发展[31]等因素的驱动作用。上述研究由于采用的数据与方法各异,因此研究结果也大相径庭,不具有普适性;大多集中研究双变量或少数几个变量,可能存在变量遗漏的问题,因此有必要在多变量的框架下对长江经济带进行实证研究,以考察能源消费、碳排放与经济增长三者之间的关系。

长江经济带横跨我国东部、中部、西部三大区域,覆盖上海、江苏、浙江、安徽、江西、湖北、湖南、重庆、四川、云南、贵州等11个省区,面积约205万km2,人口和生产总值超过全国的40%,具有独特的优势和巨大的发展潜力。2014年《国务院关于依托黄金水道推动长江经济带发展的指导意见》明确提出，要完善污染物排放总量控制制度,加强二氧化硫、氮氧化物、PM2.5(细颗粒物)等主要大气污染物的综合防治,严格控制煤炭消费总量,把长江经济带打造成“生态文明建设的先行示范带”,成为水清地绿天蓝的生态廊道。

当前，长江经济带碳排放已经成为研究热点并取得了较为丰硕的成果,主要集中在碳排放空间差异性[32,33]、驱动因素[34,35]、脱钩状态分析[36,37]、碳排放核算和减排潜力[38,39]等方面,而基于多变量框架研究能源消费碳排放与经济增长之间的关系不多。本文主要借助扩展STIRPAT模型并结合面板数据模型,以验证长江经济带是否存在碳排放与经济增长之间的倒“U”型曲线,同时研究各驱动因素对碳排放的影响程度,为长江经济带低碳经济的发展提供科学的决策建议。

1 模型构建与数据来源

1.1 能源消费的碳排放核算

由于目前我国还缺少对CO2排放量的实时监测数据,因此本文借鉴IPCC推荐的方法,根据能源消费数量与能源碳排放系数进行估算。碳排放计算公式为:

(1)

式中,C为终端能源消费产生的碳排放量;Eij为第i部门第j种能源的实物消费量(t)。根据能源平衡表中的能源分类,并借鉴万庆等[40]学者的做法,选取原煤、洗精煤、其他洗煤、型煤、焦炭、焦炉煤气、其他煤气、原油、汽油、煤油、柴油、燃料油、液化石油气、炼厂干气、天然气、热力、电力和其他能源等18种能源;αj为第j种能源折标系数(kgce/kg,气体类为kgce/m3);βj为第j种能源碳排放系数(kg/kgce)。各能源折标系数及其碳排放系数见表1。电力和热力的碳排放系数,则借鉴查建平等[41]学者的计算方法。

表1 各能源折标系数与碳排放系数

注:折标系数取自2016年《中国能源统计年鉴》,除其他能源外,各能源碳排放系数取自相关文献[15, 43, 44]中的平均值。

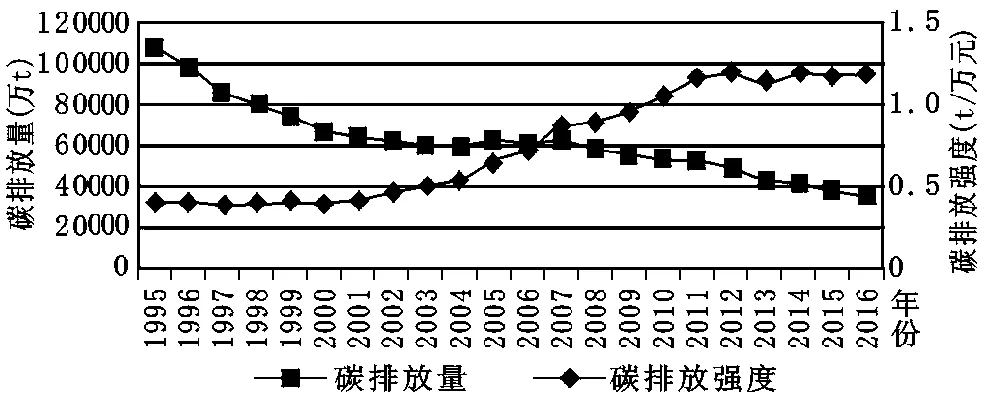
图1 1995—2015年长江经济带能源消费碳排放量

根据式(1)估算的碳排放量及其碳排放强度变化趋势见图1。由图1可知,1995—2016年长江经济带能源消费碳排放量总体保持上升趋势,从1995年的32064.7万t上升到2016年的95065.87万t,增长了196.48%;与之对应的碳排放量强度则呈现出不断逐渐下降的趋势,由1995年的1.3457t/万元下降到2016年的0.4434t/万元。可见,2002—2012年碳排放量增长非常迅速,尤其是2005—2007年各年增长率均超过10%,2007年达到峰值的15.12%,此后碳排放增长速度略有减缓,而碳排放强度在此期间一直平稳下降。

1.2 模型设定及指标选取

IPAT模型最早由Ehrlich等于1972年提出,该模型认为人类对环境的影响(I)主要是通过人口总量(P)、富裕程度(A)、技术水平(T)三者共同起作用的,即I=P×A×T。此后,York等将其扩展为非线性随机回归STIRPAT模型。该模型既克服了原有模型中各因素等比例影响环境状况不足,又可对各因素进行分解与改进,满足了各种实证分析的需要,表达式为:

I=aPbAcTde

(2)

式中,I、P、A、T分别为环境压力、人口总量、富裕程度和技术进步;a为该模型系数;b、c、d分别为各影响因素的待估计参数;e为随机误差项。

在实证分析过程中,由于简单的线性往往不能得到一致的估计结果,因此通常需要对模型两侧同时进行对数化处理,以减少异方差和偏误。结合面板数据特征,模型(2)变为:

lnIit=β0+β1lnPit+β2lnAit+β3lnTit+eit

(3)

为防止变量遗漏导致模型设定错误,更好研究长江经济带碳排放的驱动因素,本文基于长江经济带的实际情况,将STIRPAT模型的影响因子进行扩展,以尽可能全面考虑碳排放的各种影响因素。

主要影响因素包括:①人口因素(P)。人口因素分解为人口规模(POP)和人口结构(URB)两个因素：人口规模越大,生产生活中的能源需求也越大,由此会产生更多的碳排放量,预期人口规模与碳排放量呈正相关。人口结构着重于人口的城乡分布,用人口城市化水平衡量。一方面，城市化水平提高会增加能源需求,增加碳排放；另一方面，随着新型城市化的发展、城市居民素质的提高,可能降低碳排放,因此城市化水平对碳排放的影响不确定。②富裕程度(A)。富裕程度主要用来衡量经济发展对环境的影响,用人均GDP衡量富裕程度。已有研究表明，碳排放量会随着人们收入水平的提高呈现出先增长后降低的变化趋势,表现为倒“U”型的EKC关系。此外，还可能存在“U”型、“N”型、倒“N”型等关系。③技术水平(T)。技术水平主要反映了技术进步在治理环境污染时所起的作用,采用产业结构、能源强度、创新水平表征。产业结构(IND)用第二产业增加值占GDP的比重衡量,预期第二产业占比越高,则碳排放量越高;能源强度(EER)是衡量能源综合利用效率的重要指标,显然单位经济活动能源消费的降低可提升能源效率,因此能源强度降低可减少碳排放量;借助技术进步提高创新水平,可有效抑制碳排放,本文用人均专利授权量(INV)衡量创新能力。④对外开放程度。对外开放程度主要表述在开放经济的背景下，国际社会对国内碳排放的影响,采用外商直接投资(FDI)和贸易开放度(TOQ)衡量。FDI对地区环境质量的影响存在着“污染天堂”和“污染晕轮”两种假说,其影响方向不确定。进出口贸易则可以通过规模效应、技术效应等扩大碳排放,本文用进出口总额占GDP的比值来衡量贸易开放度。⑤金融发展水平(FD)。金融业发展既可以通过促进经济增长提高能源消费量,增加碳排放量;也可以给低污染低能耗企业更多的支持,通过金融业支持调整产业结构降低碳排放水平,因此其影响方向不确定。本文用信贷总量(即金融机构贷款余额+金融机构存款余额)占GDP比重来衡量。⑥环境规制(ER)。环境规制强度越大,对碳排放的抑制作用越明显,本文借鉴黄寿峰[45]、张成等[46]的做法,用工业污染治理投资额占工业增加值比重来衡量环境规制水平。

由模式(3)扩展成模式(4),具体形式为:

lnCit=β0+β1lnPOPit+β2lnURBit+β3lnGDPit+β4lnINDit+β5lnEERit+β6lnINVit+β7lnFDIit+β8lnTOPit+β9lnFDit+β10lnERit+eit

(4)

为检验长江经济带经济增长与碳排放是否存在倒“U”型的EKC关系,本文将模型(4)中的lnGDPit拆分为lnGDPit和(lnGDPit)2[47],模型(4)调整为:

lnCit=β0+β1lnPOPit+β2lnURBit+β31lnGDPit+β32(lnGDPit)2+β4lnINDit+β5lnEERit+β6lnINVit+β7lnFDIit+β8lnTOPit+β9lnFDit+β10ERit+eit

(5)

式中,β31、β32分别表示lnGDPit、(lnGDPit)2的系数。由模型(5)可得到人均GDP对碳排放量的弹性系数为:ERLA=β31+2β32lnGDPit。若β32的估计值小于零,说明存在倒“U”型环境库兹涅茨曲线,即人均GDP增加到一定水平后环境质量开始改善;反之,则不存在这种关系。

1.3 数据来源与处理

本文的面板数据由1995—2015年长江经济带11个省级行政区构成,所用数据均来自于历年的《中国能源统计年鉴》、《中国统计年鉴》、《新中国60年统计资料汇编》、《中国环境统计年鉴》、长江经济带各省市的统计年鉴和统计公报。为了消除物价上涨的影响,人均GDP以1995年为基期折算为可比价,外商直接投资数据按照当年的平均汇率进行了换算。此外，少数缺失值借助SPSS进行线性插值处理,计量分析均借助Eviews10.0软件进行,各变量的数据见表2。

2 实证分析

2.1 变量的平稳性检验

为了消除异方差,本文对所有变量均做了取对数处理。同时，为了防止虚假回归,必须对各变量的平稳性进行检验。本文采用LLC、Fisher-ADF两种方法对面板数据进行了单位根检验,检验结果见表3。检验结果表明,除LNGDP、(LNGDP)2为二阶平稳外,其他所有变量原始序列值为非平稳,但一阶差分均平稳,属于一阶单整序列,因此可以进行协整检验。

表2 各变量描述性统计结果

表3 面板数据单位根检验结果

注:括号内为P值,*、**、***分别表示在10%、5%、1%水平上显著。

2.2 面板数据的协整检验

由于本文面板数据时间序列长而截面短,故采用Pedroni′s、Johansen Fisher两种方法对模型(5)的LNC、LNGDP、(LNGDP)2进行面板数据协整检验,结果见表4。从检验结果看,模型5中Pedroni′s方法基于PP检验和ADF检验的统计量均通过了组内和组间的显著性检验,因此可拒绝没有协整关系的原假设。Johansen Fisher协整检验中也拒绝了“不存在协整关系”的原假设,因此变量之间存在着长期协整关系,可进行回归分析。

表4 Pedroni′s方法面板协整检验结果

注:零假设为变量都不协整；*、**、***分别表示在10%、5%、1%水平上显著。

2.3 碳排放影响因素分析

利用模型(5)对长江经济带、东部地区、中部地区和西部地区碳排放量的影响因素分别进行了估计,回归结果见表5。从表5得知,各模型的拟合优度均超过了98%,说明该模型的拟合程度较高,很大程度上各因素可以解释碳排放量的增长状况。

表5 面板数据回归结果

注:东部地区包括上海、江苏、浙江3省;中部地区包括安徽、江西、湖北、湖南4省;西部地区包括重庆、四川、贵州、云南4省。*、**、***分别表示在10%、5%、1%水平上显著。

从表5的面板数据回归结果可见,LNPOP系数为负且没有通过显著性检验,表明人口规模对长江经济带碳排放量影响并不明显,但在东部地区和西部地区人口规模的增长明显促进了碳排放量的增加。LNURB系数在1%的显著水平上显著为负,表明长江经济带城市化水平每提高1%,碳排放量将下降1.0116%。这主要是因为城市化水平的提高可能会带来集约化的发展模式、合理的产业布局、较强的环保意识,促使碳排放量下降,这种减排效应在经济发达的东部地区表现得较为明显。此外,中部地区和西部地区则相反,LNURB系数为正,分别为0.0682、0.1259,意味着城市化水平每提高1%,中部地区和西部地区碳排放量将分别增加0.0682%、0.1259%。可能的原因是，随着中部地区和西部地区城市化水平的不断提高,大量的农村剩余劳动力将转化为城市人口,这促使城市的生产生活能源消费需求不断增加,导致碳排放量增长,上述结论与预期大体一致。

除了西部地区以外,在长江经济带和中西部地区的LNGDP一次项系数为正，二次项系数为负,并在1%的显著性水平上通过显著性检验,表明长江经济带已经出现了较明显的EKC曲线。随着经济的持续增长,碳排放量呈现先增加后减少的趋势,经济增长水平与碳排放量呈现倒“U”型关系,这与王健、田泽等学者[48,49]的研究结果是大体一致的。上述地区人均GDP每增长1%,碳排放量将分别增加(2.1176—0.0798LNGDP)%、(4.0893—0.1510LNGDP)%、(3.0621—0.1214LNGDP)%，但西部地区的经济增长弹性系数为(0.06956+0.0421LNGDP)%。由于(LNGDP)2系数为正,表明该地区在样本期内人均GDP与碳排放量没有出现倒“U”型关系,即其富裕程度尚未到达可改善环境质量的拐点水平。这主要是样本期内西部人均GDP年均增长率达到10%,经济的快速增长、粗放的发展方式导致过度消耗能源而产生了大量的碳排放。

为了验证长江经济带能源消费碳排放与经济增长之间的关系,借鉴陈炜等[50]的方法,对上述地区的碳排放与人均GDP关系进行EKC模拟,结果见表6。

从表6可知,我国东部地区的实际人均GDP位于拐点右侧,表明目前该地区碳排放量开始降低,环境质量有所好转。

表6 长江经济带能源消费碳排放与人均GDP的EKC模拟

从技术水平看,LNIND、LNEER的系数均为正,且两者均在1%的水平上通过了显著性检验。这表明产业结构、能源强度对长江经济带的碳排放量产生了重要影响。其中,代表产业结构的第二产业占GDP比值每增加1%,碳排放量将增加0.6568%;代表能源消费水平的能源强度每增加1%,碳排放量将增加0.5020%。上述研究结果与预期一致。这可能是因为长江经济带第二产业中的“三高”产业(即高能耗、高排放、高污染)仍占据重要地位，导致能源消费量快速增长,未来长江经济带的碳减排形势严峻。代表创新水平的人均专利授权量LNINV系数也为正,并在10%的显著水平上通过了显著性检验,意味着人均专利授权量每增加1%,碳排放量将增加0.0539%。该结果与预期完全相反。可能是因为长江经济带的绿色科技创新成果较少,导致用于减排的创新成果更少。此外,在对碳排放量产生重要影响的其他因素中,LNFDI、LNFD的系数均为负值,且分别在1%、5%的水平上通过了显著性检验。其中,外商直接投资总量增加了1%,碳排放量将减少0.1334%,表明长江经济带总体上外商直接投资带来的“污染晕轮”超过了“污染天堂”效应,这可能与外商直接投资引进各种清洁技术和环境友好型产品有关。

尤其需要注意的是,我国中部地区和西部地区的LNFDI系数显著为正,这可能是因为中部地区和西部地区的第二产业增加值占GDP比重大多为50%—60%,已经具备了一定的工业化水平,容易引进发达国家的转移污染企业而沦为“污染避难所”。金融发展水平的提高对长江经济带及其三大区域的碳减排均具有明显的抑制作用,尤其是东部地区抑制作用更加明显,金融发展水平每提高1%,碳排放量将减少0.3293%,这可能是因为金融业的发展带动了长江经济带产业结构的优化，并促进了低碳经济的发展。LNTOP、LNER的系数均未通过检验,这表明贸易开放度和环境规制对碳排放量的影响并不显著。

总体上来看,在众多因素之中,经济增长依然是推动我国碳排放量增加的一个最主要因素,产业结构和能源强度的影响次之，而城市化水平、外商直接投资、金融发展则对碳排放具有较为显著的抑制作用。

3 结论

本文采用我国长江经济带1995—2016年的面板数据,基于STIRPAT模型分析了人口因素、经济增长因素、技术水平因素和其他因素对长江经济带碳排放的影响,同时验证了长江经济带“EKC”曲线的存在,主要结论为:

首先，人口规模对长江经济带碳排放量没有显著影响;城市化水平对东部地区具有显著的抑制作用,城市化水平每提高1%,碳排放量将下降0.2193%;中部地区与西部地区城市化水平对碳排放具有显著的推进作用,城市化水平每提升1%,碳排放量将分别增加0.0682%、0.1259%。

其次，碳排放与人均GDP之间呈显著的倒“U”型曲线关系,但目前只有东部地区通过碳排放的拐点,中部地区接近拐点,而西部地区碳排放量在较长时期内将持续增长。

第三，技术水平中的产业结构和能源强度都对长江经济带的碳排放均产生显著影响,其弹性系数分别为0.6568%、0.5020%,两者对中部地区和西部地区的影响远远大于东部地区,创新水平对碳排放量影响微弱。

第四，在其他影响因素中,外商直接投资、金融发展水平对碳排放有显著的抑制作用,其弹性系数分别为-0.1334%、-0.1364%。其中,外商直接投资对东部地区碳排放具有明显的抑制作用,而对中部地区与西部地区具有推进作用,金融发展水平对东部地区的抑制作用最明显。此外,贸易开放度和环境规制没有通过显著性检验,两者对碳排放量的影响均较小。