北斗系统测站钟差短期预报模型比较及其在单星定轨中的应用∗

陈 倩 陈俊平 于 超 张益泽

(1 中国科学院上海天文台上海200030)

(2 中国科学院大学北京100049)

(3 中国科学院大学天文与空间科学学院北京100049)

(4 东京海洋大学海事系统工程系东京1358533)

1 引言

各全球卫星导航系统(Global Navigation Satellite System, GNSS)的地面跟踪站都配备有高精度的氢原子钟、铷原子钟或者铯原子钟[1].这些高精度的接收机钟使得对测站钟差预报成为可能, 对机动卫星轨道快速恢复具有实际工程应用价值.

由于北斗系统采用了混合星座, 因此机动较为频繁, 机动期间采用几何定轨方法进行卫星轨道确定以保证北斗无线电定位服务(Radio Determination Satellite Service,RDSS)正常工作; 北斗卫星机动结束后开始积累观测数据, 在满足系统数据时长要求前对该卫星采用单星定轨策略进行轨道快速确定, 以确保卫星无线电导航服务(Radio Navigation Satellite Service, RNSS)卫星可用性.几何法定轨以及单星定轨两种技术将测站钟差作为已知量以减少待估参数来提高定轨的精度[2–4].但是由于运控系统各业务处理调度时间有差异, 轨道机动恢复期间获取的测站钟差数据相对于伪距观测数据会有部分缺失, 这将增加定轨数据积累的时间进而影响轨道恢复的周期, 制约卫星可用性.解决这一问题的有效途径是对测站钟差进行预报, 进而补偿钟差数据.

针对钟差预报方面的研究, 国内外研究学者的研究较多地是针对卫星段高性能的原子钟[5], 针对地面段的测站钟差建模及应用的研究较少, 并且鲜有钟差预报对精密定轨影响的分析.常用的钟差预报模型有2次多项式(QP)模型、谱分析模型、灰色(GM)模型等[6–9]以及以上各种模型的改进模型及综合多种模型的组合模型.其中QP模型物理意义明确且建模简单, 能反映钟自身的物理特性, 谱分析模型可以估计定轨解算出的站钟与轨道耦合的周期特性, GM模型可使用少量数据建模.本文采用2次多项式模型、通过频谱分析建立的附加周期项模型和灰色模型, 分别对测站钟差进行预报, 评估了不同模型的拟合及预报性能, 并对比分析了不同预报模型获取的测站钟差在北斗单星定轨中应用的性能.

2 北斗系统单星定轨及钟差预报

2.1 单星定轨及钟差预报模型

常规情况下北斗系统采用多星定轨模式进行整网轨道确定[10], 在存在机动卫星时,多星定轨剔除该卫星, 计算其他卫星的轨道、卫星钟差以及测站钟差等参数.并将计算的测站钟差当成已知量作为单星定轨的输入.单星定轨采用了传统动力学定轨模式, 考虑了地球非球形引力、固体潮、海潮摄动、相对论、太阳光压、地球反照辐射压等各类轨道摄动力.采用单星定轨, 测站r对卫星s的伪距观测方程简写如下[4–5]:

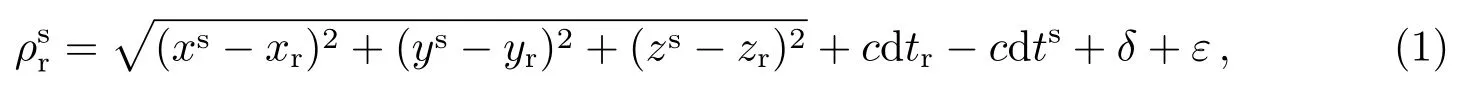
图1为常规单星定轨观测数据以及测站钟差输入时序的示意图.从图中看到, 起始时刻t0是定轨使用数据起始历元时刻, 终止时刻t1是多星定轨解算的测站钟差数据最后历元时刻, t是启动单星定轨的当前时刻.常规单星定轨使用的有效数据取决于多星定轨解算的测站钟差终止时刻t1.利用多星定轨估计得到的测站钟差进行单星定轨时, 即使当前时刻t存在观测数据, 单星定轨最后历元也只能是终止时刻t1.在此情况下, t1到t时刻该卫星的广播星历需要进行预报, 按照目前北斗系统数据处理的规范, 该时段最长可达2 h, 轨道径向预报误差将超过数米, 系统服务性能将受到影响.

图1 单星定轨中使用的多星定轨测站钟差及预报测站钟差示意图Fig.1 The station clock errors from the Multi-satellite Orbit Determination (Multi-POD) and prediction,which are used in the fast orbit determination

图1中, 从单星定轨使用数据终止时刻t1至当前数据时刻t, 可采用钟差预报模型对多星定轨获取的测站钟差进行预报, 实现当前时刻单星定轨处理, 从而提高卫星轨道的实时性和性能.

钟差预报的常用模型包括QP和GM等.对于北斗系统, 由于卫星轨道和钟差存在强相关性, 钟差还存在周期特性, 可采用附加周期项模型(PM)[11–13].

2次QP可以明确反映其钟速和钟漂的基本物理特性, 公式如下:

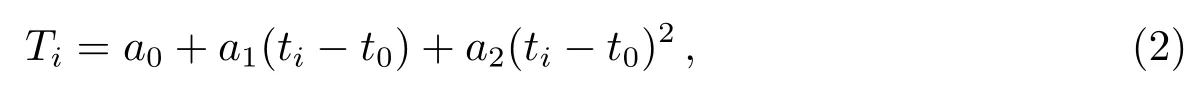
其中Ti是第i历元的测站钟差, t0为参考时刻, ti为历元时刻, a0、a1、a2分别为参考时刻的钟差、钟速和钟漂.多项式系数a0、a1、a2依据最小二乘法求得.

PM表达式如下:

其中, ∆t = ti−t0, p = 1,2···m, m的大小由功率谱决定, Ap和Bp分别是第p个主周期项对应的振幅, ωp是第p个主周期对应的频率.求解时需先利用2次多项式去除趋势项部分来得到残差序列, 然后对残差序列通过傅里叶变换进行频谱分析以获得各主频项ωp,最后对式中其余各项系数利用最小二乘法同时求解.

对于GM, 设有原始钟差序列X(0)=[x(0)(1),x(0)(2),··· ,x(0)(n)], 通过一次累加生成新序列X(1)=[x(1)(1),x(1)(2),··· ,x(1)(n)].其中n为钟差数据的个数, x(1)(k) =对X(1)其一阶微分方程式如下:

上式即为GM的白微分方程, 其中a为发展灰数、b为控制灰数.采用回归分析求其解为:

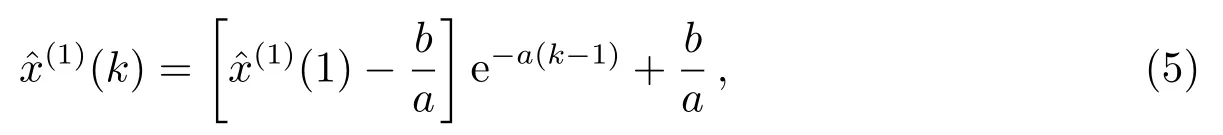
不同模型特性不同, 通过分析各模型对北斗系统多星定轨测站钟差的拟合预报性能, 并在此基础上进行单星定轨的评估, 从而为提高北斗系统单星定轨的实时性提供参考.

2.2 钟差预报及单星定轨精度评估

在测站钟差的拟合及预报中, 采用均方根误差(Root Mean Square, RMS)进行精度评估.公式为:

其中, RMSq为第q组拟合或预报误差的RMS统计, Yj为第j历元的钟差拟合或预报值,yj为对应历元时刻的多星定轨测站钟差原始值, l为历元数.

北斗系统多星定轨的精密轨道精度比单星定轨高一个数量左右, 因此将其作为参考评估单星定轨的卫星轨道精度.轨道径向偏差对用户影响最大, 因此轨道评估包含了轨道径向偏差和3维位置偏差, 计算公式如下:

其中RMSR,q、RMSP,q分别为第q组轨道径向及3维精度的RMS统计, Rj为第j历元单星定轨的轨道径向值, rj为对应历元时刻多星定轨的轨道径向值, Pj为第j历元单星定轨的轨道3维值, pj为对应历元时刻多星定轨的轨道3维值.

3 数据分析

3.1 钟差拟合与预报结果

采用北斗系统2018年332 d解算的多星定轨测站钟差数据, 数据间隔为1 min, 对参与定轨的6个测站的站钟分别采用QP、PM和GM进行钟差拟合及预报分析.

实验按照北斗地面运控数据处理的规范进行设计.其中测站钟差拟合弧长选择为2 h, 自02:00—21:00每整点拟合及预报一次, 即连续测试20组.分别计算各测站各模型拟合弧段RMS和预报1 h、2 h的RMS.结果如图2–4所示.

图2是各测站每次拟合的精度时序图, 从图中可以看出, 采用附加周期项模型的拟合精度较高且较稳定, 对6个测站的拟合精度在0.15 ns以内.灰色模型和多项式模型在不同的拟合时段体现出明显波动性, 2次多项式模型对6个测站的拟合精度都在1 ns以内, 灰色模型的拟合精度总体较差.

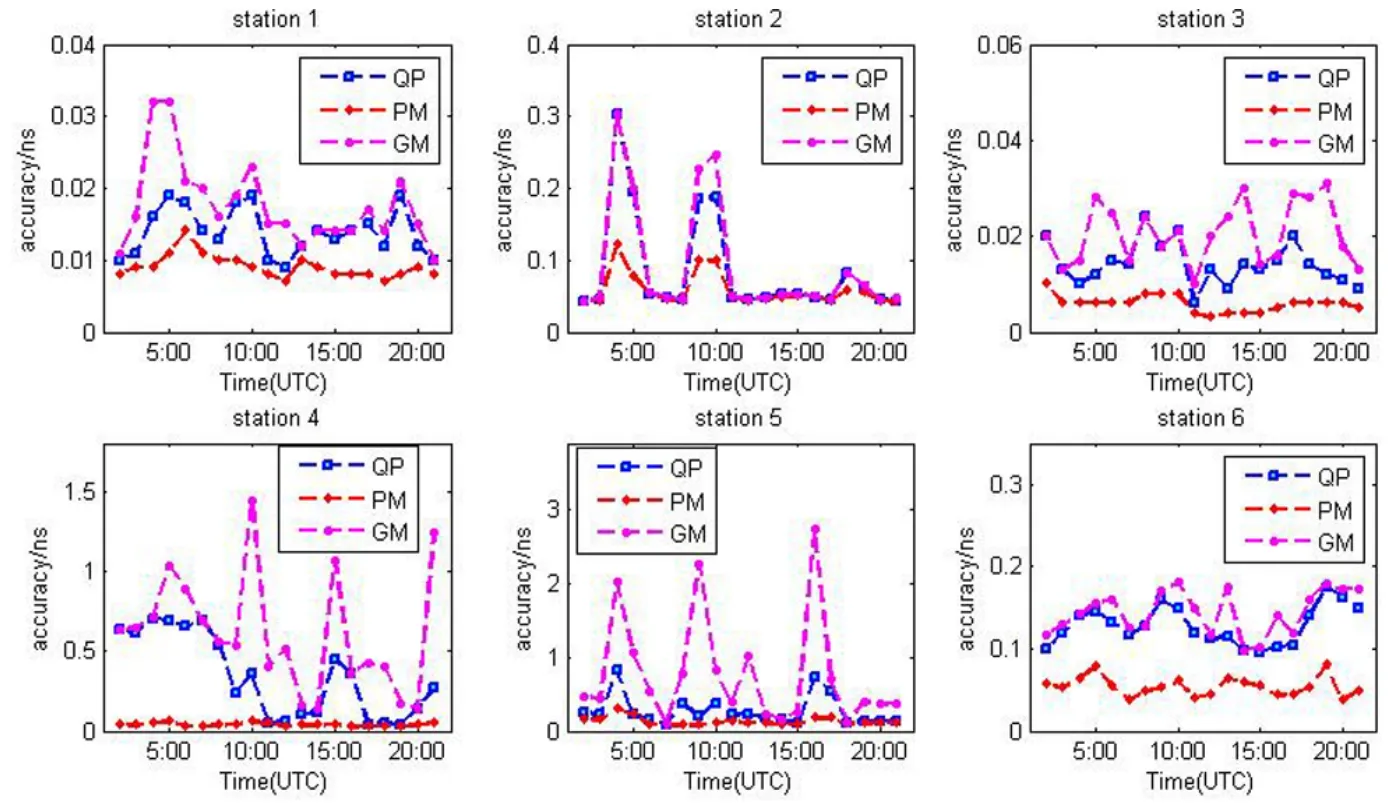
图2 测站钟差拟合RMSFig.2 The RMS of station clock error fitting

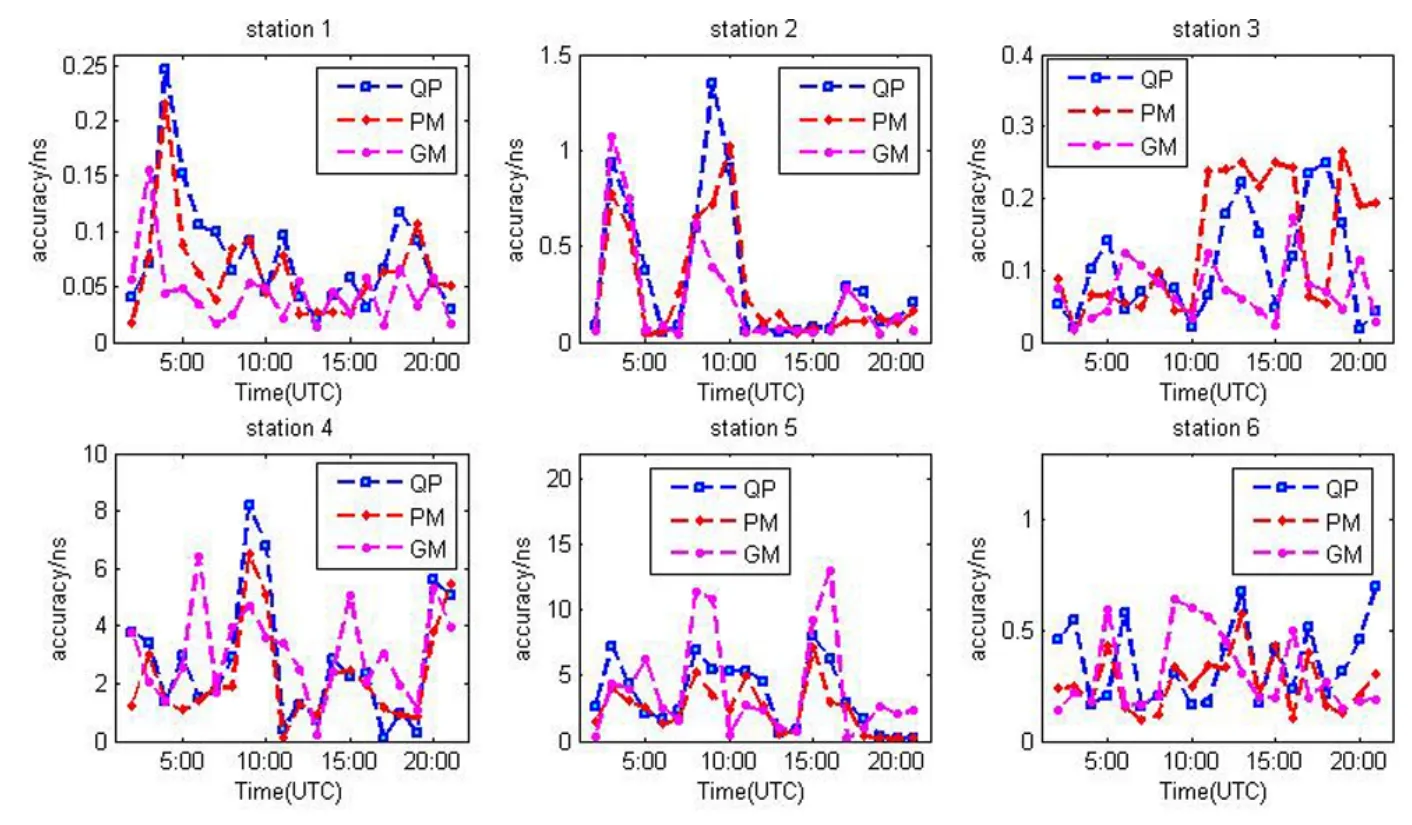
图3 1 h测站钟差预报RMS统计Fig.3 The RMS of 1 h prediction for the station clock error

同种模型针对不同测站的拟合精度也不同.所有模型针对测站1和3所有组的拟合误差都在0.05 ns以内, 所有模型针对测站2和6所有组的拟合误差都在0.3 ns以内.所有模型针对测站4和5的拟合精度明显比其他测站要差.这说明测站4和5配置的原子钟的稳定度相对较差.

图3给出了各测站每次预报1 h钟差的RMS.3种模型对测站1、2、3、6的预报精度都较好, 大多数的预报误差都在0.5 ns以内, 各模型间同时刻预报的差异绝大多数都在0.1 ns以内, 可以认为3种模型针对这几个站预报1 h的精度水平相当.而对于测站4和测站5, 其钟差预报在不同的时段差异较大, 个别时段采用2次多项式模型或者灰色模型的最大误差达到8–12 ns, 采用附加周期项模型相对稳定一些.

图4是各测站每次预报2 h钟差的RMS.测站1、2、3绝大多数时候预报2 h的精度在0.8 ns以内, 同一时刻采用3种模型的预报精度在大多数时段较为吻合.在个别时段使用2次多项式模型预报精度发生跳变.对于测站4、5和6使用2次多项式模型和灰色模型在个别时段的预报精度较差, 测站4和5采用2次多项式模型和灰色模型时, 甚至个别时段的预报误差超过15 ns.

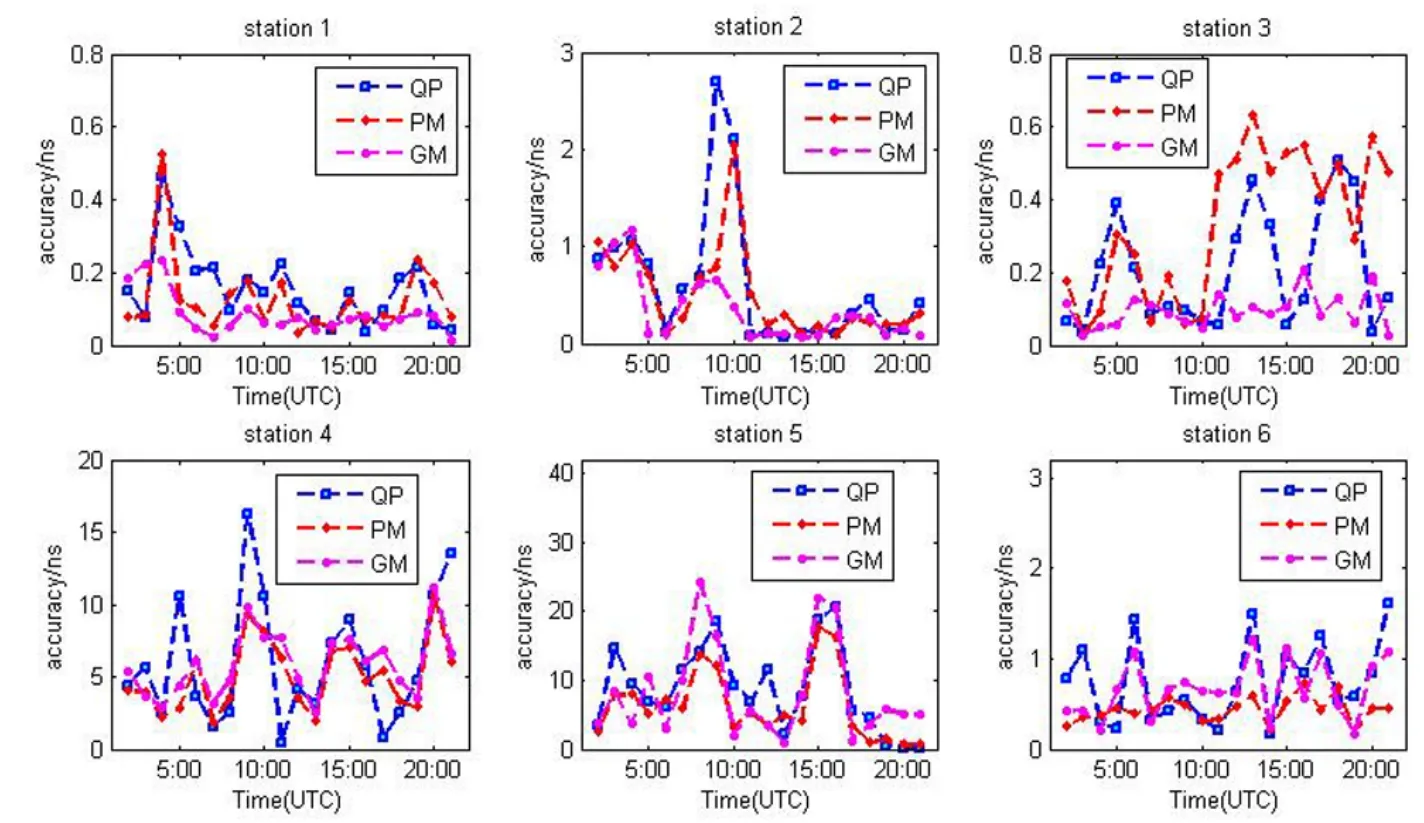
图4 2 h测站钟差预报RMS统计Fig.4 The RMS of 2 h prediction for the station clock error

对各测站3种模型20组的拟合RMS、预报1 h的RMS和2 h的RMS精度求取平均值,如表1所示.

根据表1统计, 就拟合精度而言, 3种模型中附加周期项模型的拟合效果最好, 针对所有测站的拟合精度优于0.15 ns, 2次多项式对所有站的拟合精度优于0.4 ns, 灰色模型对所有站的拟合精度优于0.8 ns.采用2次多项式模型、附加周期项模型、灰色模型对6个测站的平均拟合精度分别为0.14 ns、0.05 ns、0.27 ns, 可见采用附加周期项模型的拟合精度最高.

就预报精度而言, 预报精度随预报时长增加而变差, 同一模型对不同测站的预报精度也有差异, 如测站4和测站5的钟差拟合及预报明显较差.适用于测站1、2、3的最优模型为灰色模型, 其次为附加周期项模型, 两种模型差异较小; 测站4、5、6的最优模型为附加周期项模型, 其明显优于其他两种模型.采用2次多项式模型、附加周期项模型和灰色模型对6个测站预报1 h的平均精度分别为1.17 ns、0.88 ns、1.28 ns; 预报2 h的平均精度分别为2.72 ns、2.09 ns、2.53 ns.从所有站的平均精度来看, 采用附加周期项模型效果较好, 这是因为多星解算的离散钟差点也存在类似轨道的周期波动[14], 采用附加周期项模型可以较好地消除这一波动.

表1 各测站钟差拟合及预报精度(单位: ns)Table 1 The accuracy of station clock error fitting and prediction (unit: ns)

3.2 单星定轨结果分析

将以上各模型预报的测站钟差引入单星定轨, 对C01–C04 4颗GEO (Geosynchronous Orbit)卫星和C06–C10 5颗IGSO (Inclined Geosynchronous Satellite Orbit)卫星进行单星定轨测试, 统计每颗卫星各模型下的20次测试的轨道精度均值, 进一步评估各模型在定轨中的性能.为更好评估各模型单星定轨的性能, 还将常规策略单星定轨获得的轨道进行相应时长的预报, 并与精密星历进行比较, 评估其精度.图5为各模型预报1 h的测站钟差用于9颗卫星单星定轨时, 该时段内的径向偏差和3维位置偏差结果图.

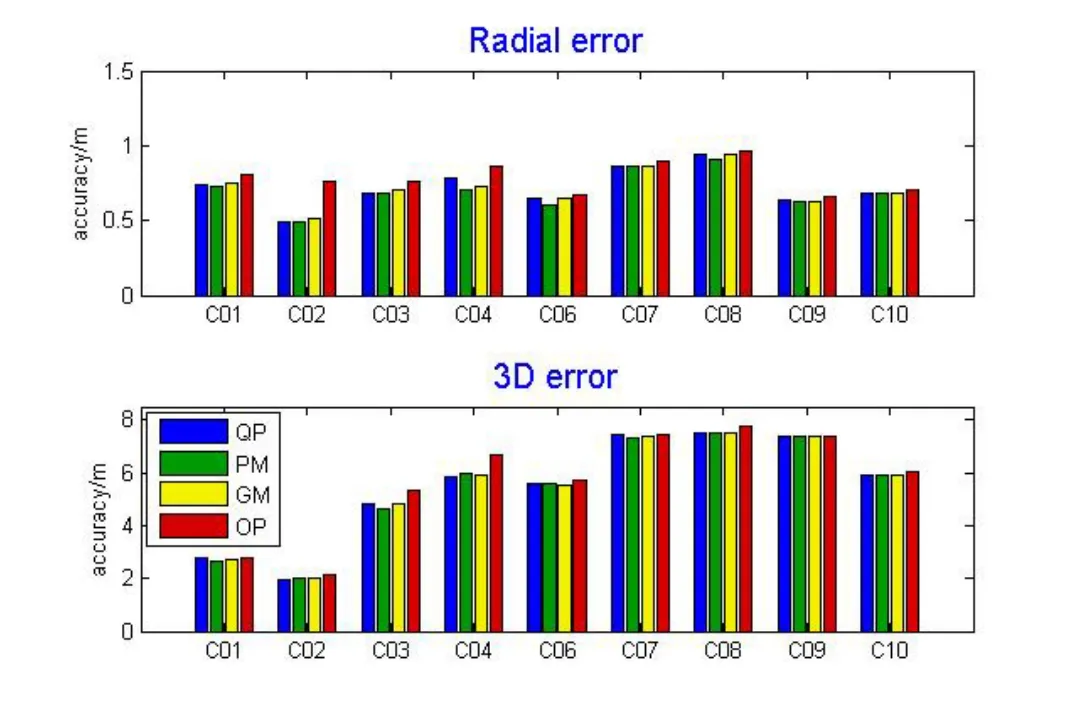
图5 各模型1 h测站钟差预报应用于单星定轨的精度及其与常规单星定轨相应弧段外推1 h的精度对比(OP为常规单星定轨).Fig.5 The comparison of the precision of fast orbit determination with the application of 1 h station clock error prediction by different models and the precision of original fast orbit determination with 1 h extrapolation in the same arc (OP is the original fast orbit determination).

可以看出将预报1 h钟差引入单星定轨时, 单星定轨该时段内的径向精度在0.54–0.81 m之间, 3维位置精度为2.0–7.5 m之间; 常规单星定轨在相应弧段为外推1 h的预报轨道, 其径向精度在0.66–0.85 m之间, 3维精度在2.2–8.1 m之间.3种钟差预报模型下各卫星定轨径向精度差异大多在毫米级, 对3维位置误差互差在20 cm以内, 精度基本相当,且都好于常规单星定轨轨道预报的精度.

图6为各模型预报2 h的测站钟差用于9颗卫星单星定轨时, 该时段内的径向偏差和3维位置偏差结果图.图中看到, 原始单星定轨在该弧段为外推2 h的预报轨道, 其径向精度在0.71–1.02 m以内, 3维精度在2.5–8.5 m之间.采用不同模型卫星的径向偏差差异比较明显, 尤其是GEO卫星利用附加周期项模型后轨道精度提升效果明显; 不同预报模型下各卫星轨道3维互差不超过30 cm.3种模型钟差预报用于定轨的精度都好于系统同时刻定轨的原始轨道, 且大多数卫星采用附加周期项模型的径向精度最好.

图6 各模型2 h测站钟差预报应用于单星定轨的精度及其与常规单星定轨相应弧段外推2 h的精度对比Fig.6 The comparison of the precision of fast orbit determination with the application of 2 h station clock error prediction by different models and the precision of original fast orbit determination with 2 h extrapolation in the same arc

表2给出了每颗卫星不同模型单星定轨精度的统计值.从表2看出, 预报1 h测站钟差用于单星定轨, 3种钟差预报模型卫星轨道径向偏差均值分别为0.676 m、0.656 m、0.673 m, 互差在2 cm以内, 位置偏差均值分别为5.570 m、5.501 m、5.529 m, 互差在0.069 m以内.各模型相对于常规单星定轨轨道预报径向精度0.755 m和3维精度5.902 m分别提高了10.40%、13.08%、10.75%和5.62%、6.80%、6.31%.

当预报2 h测站钟差用于定轨时, 3种钟差预报模型卫星轨道径向偏差均值分别为0.725 m、0.693 m、0.723 m, 互差在3 cm以内, 位置偏差均值分别为5.767 m、5.672 m、5.679 m, 互差在0.07 m以内.采用附加周期项模型效果最好, 各模型相对于常规单星定轨轨道预报径向精度0.840 m和3维精度6.187 m分别提高了13.71%、17.53%、13.89%和6.78%、8.33%、8.21%.

表2 各预报模型用于POD的精度(单位: 米)Table 2 The accuracy for each prediction model used in POD (unit: m)

4 结论

该文对北斗系统的测站钟差分别采用2次多项式模型、附加周期项模型和灰色模型进行了钟差预报评估测试, 并按照北斗系统数据处理的规范, 将其预报1 h和预报2 h的测站钟差应用于单星定轨, 结论如下:

(1)多星解算的测站钟差中含有未完全分离的轨道误差, 采用附加周期项模型的钟差拟合精度最高: 所有测站钟差的拟合精度都在0.15 ns以内, 平均拟合精度达到0.05 ns.

(2)各测站的站钟性能不同, 测站钟差预报随预报时间增长而增大.采用2次多项式模型、附加周期项模型、灰色模型对6个测站预报1 h的平均精度分别为1.17 ns、0.88 ns、1.28 ns; 预报2 h的平均精度分别为2.72 ns、2.09 ns、2.53 ns.从所有站的平均精度来看, 采用附加周期项模型效果较好.

(3)将各模型预报1 h的钟差结果分别用于定轨, 各模型定轨径向精度平均互差小于2 cm; 将各模型预报2 h的钟差结果分别用于定轨, 各模型定轨径向精度平均互差小于3 cm.试验结果表明采用附加周期项模型应用于单星定轨的效果最好, 其预报1 h、2 h用于定轨时相对常规单星定轨轨道预报径向精度分别提升了13.08%、17.53%, 3维精度分别提升了6.80%、8.33%.