一种分布式雷达网中的航迹关联方法

白 晶，杨广厅,李子杰

(1.中国电子科技集团公司第五十四研究所，河北 石家庄 050081；2.北京市遥感信息研究所，北京 100192)

0 引言

分布式雷达网[1-2]数据融合过程中，当融合中心获得局部传感器送来的局部航迹后，需要对局部航迹进行航迹分类，然后再对归类后的航迹进行航迹融合，最后形成系统航迹[3-8]。直接对整个目标区域的多条局部航迹进行两两关联，运算量会非常大，每2条航迹间进行关联时，都需要求得局部雷达传感器跟踪滤波器提供的检验统计量，求该检验统计量时要计算矩阵的求逆、相加和相乘[9-12]。目前，虽然计算机运算速度非常快，但是矩阵的运算量非常大，尤其是求逆运算。在雷达网航迹关联中[13-16]，由于多部雷达同时跟踪多个目标，局部航迹的数量是实际目标数量的几倍，给直接进行航迹关联带来了很大的负担。所以对雷达网多条局部航迹选择一种关联策略，将航迹关联次数降低是必要而且必需的。

从实际工程应用角度出发，提出了一种区域航迹关联策略。其核心思想是将目标区域分成若干小区域，落在小区域内的航迹与其相邻区域进行关联比较，而与它不相邻的区域无需关联。每个区域(包括大区域和小区域)赋给相应的一个坐标，并与目标的平面直角坐标相对应。最后根据目标航迹的区域坐标和关联准则，对落在相邻区域内的航迹间进行航迹关联。

1 目标区域相关定义

1.1 目标区域和目标子区域

目标区域是指雷达网所覆盖的目标数据处理区域，雷达网对落在该区域内的目标航迹均需要进行航迹关联。目标子区域则是整个目标区域划分成若干相等的区域后的小区域，可划分成更小的子区域。

1.2 区域坐标

区域坐标选用类似方格坐标系(一种按地球球面经纬度分区的坐标系)的划分方法。目标区域划分成若干相等的区域后，每个目标子区域的编号都是一位十进制数。

1.3 区域航迹集合

定义下面的集合为区域航迹集合：

TSci={T1,T2,T3，…，TNc}，i=1,2,3，…，

式中，TNc为在第i个关联周期落在区域坐标为c的子区域中的航迹；Nc为落在该子区域内的航迹总数，也是整个集合的元素个数，显然Nc≥0。

1.4 相邻区域坐标集合

定义下面的集合为相邻区域坐标集合：

Sca={cci|ci为区域坐标为c的子区域相邻的所有区域的坐标}。简单起见，Sca的元素cci简化为ci。

定义Scw={y|y为所有子区域的坐标}为坐标全集，则不相邻区域坐标集合为：

2 区域航迹关联准则

整个目标区域被划分成3级3×3的区域后，其方格坐标的分布情况如图1所示。给出了1号方格中所有小小方格的坐标和所有中方格边界上的坐标。

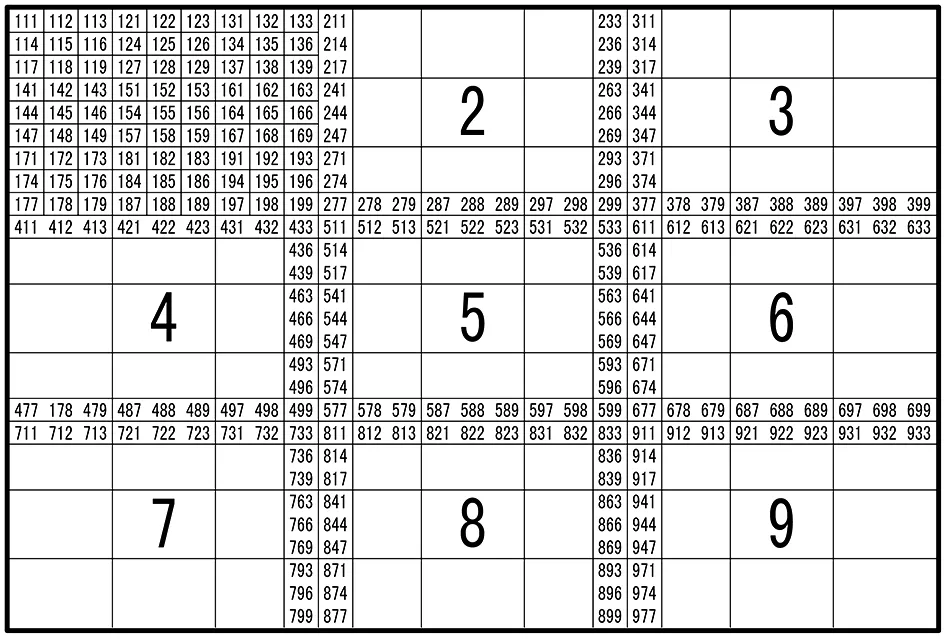
图1 区域方格坐标系示意Fig.1 Regional square grid coordinate system

区域坐标集合Sca相对应的区域航迹集合设为

⋮

定义如下关联准则：

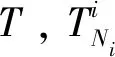
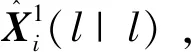
U1={1,2,…,n1}，U2={1,2,…,n2}，

那么集合U1，U2中的航迹之间的关联验证问题变为如下的假设检验问题：

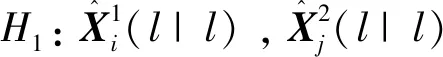
采用文献[3]中的加权航迹关联算法，可构造如下的检验统计量：

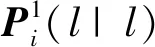
3 特定目标批数和覆盖率下的航迹关联

以上讨论了航迹间的关联准则，现在约定区域内部和相邻区域间的航迹关联准则。首先在区域内部进行航迹关联，其次在相邻区域之间进行航迹关联，区域内部进行关联时，在未关联航迹与已关联航迹间进行关联，然后在未关联航迹与未关联航迹间进行关联。区域之间进行关联时，也在未关联航迹与已关联航迹间进行关联，然后在未关联航迹与未关联航迹间进行关联。

假设目标区域的雷达序号为：1,2,3，…,R，这里R为雷达覆盖率。某个子区域对应的航迹集合TS表示为：

式中，mik，mjk分别代表航迹集TSi，TSj相对应的源自雷达k的未关联航迹数；nik，njk分别代表航迹集TSi，TSj相对应的源自雷达k的已关联航迹数；Mi，Mj分别代表航迹集TSi，TSj相对应的所有未关联航迹数；Ni，Nj分别代表航迹集TSi，TSj相对应的所有已关联航迹数。在此基础上进一步讨论分区前后的航迹关联次数。在计算航迹关联次数时，考虑关联次数最多的极限情况。

3.1 分区前的情况

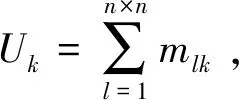
分区前的所有航迹关联次数也由未关联航迹与已关联航迹之间的最大关联次数、未关联航迹与未关联航迹之间的最大关联次数组成。

(1)未关联航迹与已关联航迹之间的关联次数Nbef1：

(1)

(2)未关联航迹与未关联航迹之间的关联次数Nbef2：

(2)

根据式(1)和式(2)可得分区前的航迹关联总次数Nbef：

Nbef=Nbef1+Nbef2。

(3)

3.2 分区后的情况

(1)航迹集TS内部关联次数Nint

① 未关联航迹与已关联航迹之间的关联包括源自每部雷达的未关联航迹与其他雷达的已关联航迹之间的最多关联次数。那么有：

(4)

② 未关联航迹与未关联航迹之间的关联包括源自每部雷达的未关联航迹与其他雷达的未关联航迹之间的最多关联次数。那么有：

(5)

根据式(4)和式(5)可得分区后的航迹集合内部关联总次数:

Nint=Nint1+Nint2。

(6)

(2)相邻航迹集TSi与TSj之间的关联次数Nbetw

①TSi中未关联航迹与TSj中已关联航迹之间的关联包括TSi中源自每部雷达的未关联航迹与TSj中其他雷达的已关联航迹之间的最多关联次数。那么有：

(7)

②TSj中未关联航迹与TSi中已关联航迹之间的关联包括TSj中源自每部雷达的未关联航迹与TSi中其他雷达的已关联航迹之间的最多关联次数。那么有：

(8)

③TSi中未关联航迹与TSj中未关联航迹之间的关联包括TSi中源自每部雷达的未关联航迹与TSj中其他雷达的未关联航迹之间的最多关联次数。那么有:

(9)

根据式(7)～式(9)可得:

Nbetw=Nbetw1+Nbetw2+Nbetw3。

(10)

根据式(6)和式(10)可得分区后的相邻航迹集合间的关联总次数Naft：

Naft=Nint+Nbetw。

(11)

4 试验验证

从一个典型实例出发，说明分区前后的航迹关联次数的变化情况。假设目标区域是400 km的方形区域且被划分成3级3×3的子区域。每个小小方格的长宽约14.8 km。假设某一时刻航迹点平均地分布在区域坐标第一位为3，6，9的中方格内，落在每个小小方格内的目标数设为8批，覆盖率为3。根据图1可知，相邻区域有3个的小小方格共有4个，相邻区域有5个的小小方格共有64个，相邻区域有8个的小小方格共有175个。所以，在计算分区后的航迹关联次数时对航迹集合内部需要考虑243次，而对航迹集合之间需要考虑866次。为了便于计算，设

mik=nik=mjk=njk=4;k=1,2,3，

将它们代入式(1)～式(11)可得：

Nbef=Nbef1+Nbef2=8 503 056，

Naft=243×Nint+866×Nbetw=201 264。

显然，分区后的航迹关联次数比分区前的航迹关联次数大大降低了。

5 结束语

本文从实际工程应用的角度出发，提出了一种可工程化的区域多雷达多航迹关联方法，该方法特别适合于目标区域中的未关联航迹数量较多的情况下使用，当目标航迹越集中该方法的效率越高。当目标区域中的未关联航迹数量较少的情况下，以未关联航迹为基准航迹建立潜在同源目标条带，落入该条带内的未关联航迹和已关联航迹均与基准航迹进行关联验证即可。