小学数学教学中分类和有序思想的培养——人教版《义务教育教科书·数学》（三年级下册）“搭配”教学赏析

王丽杰，王辉，孙健苡

(吉林省松原市教育学院，松原市前郭县哈萨尔路小学)

数学思想承载了独特、鲜明的学科育人价值，是名副其实的学科素养。在上个世纪，很多数学教师和教学研究人员就认识到了数学思想的价值，但是由于没有把其纳入课程目标，所以数学思想就成为可渗透可不渗透、可学可不学的软任务。现在，随着《义务教育数学课程标准（2011年版）》把“数学思想”写进了“四基”里面，基本目标也由多年来很多教师“耳熟能详”的“双基”变成了“不太习惯”的“四基”。数学思想融入小学数学课程经历了从内容渗透到成为课程目标的过程。数学思想作为“四基”目标之一提出来，足见其重要意义。那么，如何让数学思想在课堂中自然落下来？下面以人教版《义务教育教科书·数学》三年级下册“搭配”为例，体验孙健苡老师在“操作、比较、感悟、提升”“动态式板书”和“延伸拓展”三个环节中，让数学思想象呼吸一样自然落地。

一、在教学过程中让分类和有序思想生长

（一）在操作中体验

师：同学们，请你们用手中的图片摆一摆，二件上装和三件下装能搭配几套衣服？并把摆的过程用自己喜欢的方式记录不来。

生：（展示操作结果，如图1到图6）

图1

图2

图3

图4

图5

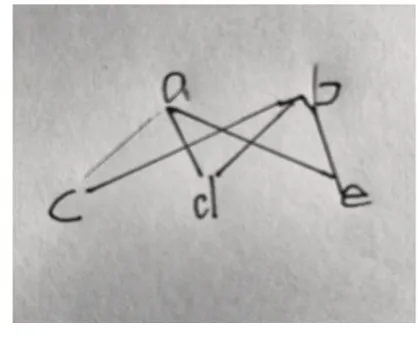
图6

给学生一个“支点”，学生就能撬动数学这个“地球”。这个“支点”就是思想方法。数学知识是显性的，数学思想方法是隐性的。教师要借助数学知识这一载体让学生自然地悟出来。孙老师在上面的教学过程中作出了这样的努力：学生自己操作、自己比较、自己感悟——人家为什么没重复也没遗漏？原来是先分上装和下装两种情况，然后再用其中一件上装分别和三件下装搭配……这个悟是“润物细无声”的。在这个过程中，孙老师让学生自内而外生长出了分类和有序的思想方法，而不是灌输给学生。这样的教学设计体现了现代认知心理学的教学思想：学习不是由外及内的灌输而是自内而外的生长。

二、在动态板书中让分类和有序思想落地

孙老师在上面的“操作、比较、感悟、提升”环节中，逐渐地填写板书，我们称之为“动态式板书”。（如表1）

表1 课题：搭配中的数学问题

在教学中，用符号运算和推理来对数学对象进行抽象，是分类和有效思想落地的主要途径。符号意识是《义务教育数学课程标准（2011年版）》提出的核心词之一，作为事物共同属性的标志，它的抽象不是一朝一夕就能完成的，需要贯穿于学生数学学习的全过程。从小开始培养，能让学生的抽象思维提前发展，并养成用代数思维解决数学问题的习惯。孙老师巧妙地运用“动态式板书”，让学生经历有文字叙述、有文字和连线、有图形、有符号的变化过程，当学生遇到具体事物表达起来比较麻烦的情况时，会自然而然地用符号来代替，从而乐于成为符号的创造者。不仅如此，更重要的是孙老师让学生知道了符号可以像数那样运算和推理，知道了通过符号运算和推理得到的结果具有一般性。a、b、c、d……可代表服装，可代表饮食。这样就有利于学生抽象思维能力的培养。

三、在延伸拓展中让分类和有序思想生根

孙老师在基本练习后，出示了下面四个拓展题。

1.在二件上衣的基础上增加3件、4件……，有多少种搭配？并借助前面的板书填上。

2.在3 件下装的基础上增加4 件、5 件……，也借助前面的板书填上。

3.数一数，下图中共有多少条线段？

4.数一数，下面第一幅图中共有多少个角？下面第二幅图中共有多少个三角形？

数学知识面广量大，是无论如何也学不完的，数学题更是无论如何也做不完的，但是，数学思想方法是有限的。我们追求的价值在于教给学生用有限的方法解决无限的数学问题。因此，我们要明确，无论是搭配问题、数线段问题、数角问题还是更复杂的数三角形问题及长方形问题，表面上看是5 种不同类型题，其实实质上就是分类和有序的思想方法。教学中，重点是教会学生用一种思想方法解5 种甚至更多种不同类型的问题。孙老师在延伸拓展环节中，有意识地教学生学会了这种数学思维和眼光。增加一件上装还是增加二件……n件，实质上都是分类有序的思想方法。