基于三域特征提取和GS-SVM的ECG信号智能分类技术研究

方红帏, 赵 涛, 佃松宜

(四川大学电气工程学院， 成都 610065)

1 引 言

心电图(Electrocardiogram，ECG)是医生诊断患者是否患有心脏病的关键，一个完整的心跳包括P、Q、R、S、T和U波等几部分，它们都反映一定的生理信息.医生可以根据各部分的波形异常来判断一个人是否生病.医生对ECG的解读往往是基于经验的，他们的判断依赖于ECG信号中基于时域的一些病因的描述，实际上除了时域，还可以从其他域如频域、小波域等去诊断ECG信号.为了帮助医生快速做出判断，提高患者的就诊效率，本文对ECG信号的智能分类技术进行了研究.

ECG信号的分类是模式识别中的一个很好的课题，许多学者对此进行了研究.对于原始ECG信号，已有学者采用小波变换[1-2]，中值滤波和陷波滤波器[3],稀疏导数分解[4]等方法去噪，但这些方法往往不能同时去除工频干扰，基线漂移，肌电干扰等噪声.去噪后的信号用于提取特征，有学者用时域特征分析[1，5]，频域及时频域特征分析[4]，小波域特征分析[2，3，6]，主成分分析(Principal Component Analysis，PCA)[1，7]及独立主成分分析(Independent Principal Component Analysis，ICA)[7]等方法.然而，这些方法提取的特征比较片面，不能全面的表达ECG信号.特征提取的目的是为了更好地将ECG信号分类，常用的方法有支持向量机(Support Vector Machine，SVM)[1，2，5，7-9]，随机森林[4]，神经网络[6],深度置信网络和主动学习[9]等，但是对于一种分类方法，如何选择合适的参数或学习框架以达到最好的分类效果也是一个难题.

本文采用连续小波变换(Continuous Wavelet Transform, CWT)对原始ECG信号进行预处理，可同时去除各种干扰.然后从时域、频域和小波域中分别提取特征，把这些特征归一化后结合GS-SVM(基于网格搜索的SVM)对ECG信号进行分类.最后用基于混淆矩阵的评价指标来评价算法的性能.

本文提出的ECG信号检测方法主要包括ECG信号的获取、预处理及分割、特征提取和归一化，最后采用GS-SVM进行分类.整个流程图如图1所示.

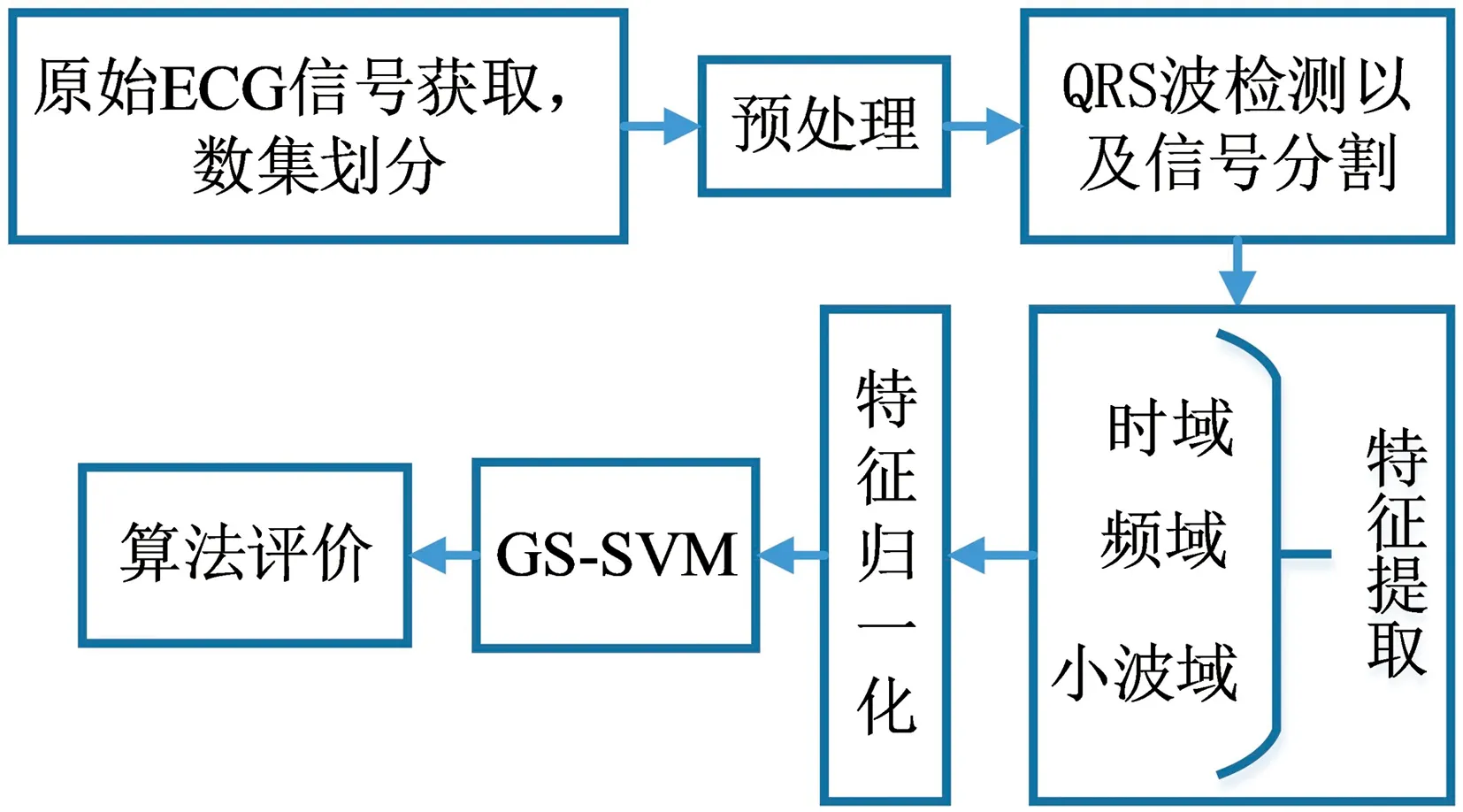
图1 ECG信号分类流程Fig.1 The process of ECG signal classification

本文的数据来源于MIT/BIH的心律失常数据库.该数据库包含48组30 min ECG信号，ECG数据采样频率为360 Hz.每组数据都从两个引导通道收集.读取48组ECG数据，选择合适的数据量进行研究.标定正常—N;左束支传导阻滞—L;右束支传导阻滞—R;所有其他ECG信号类型为“其他”—“O”,数据集划分如表1所示.

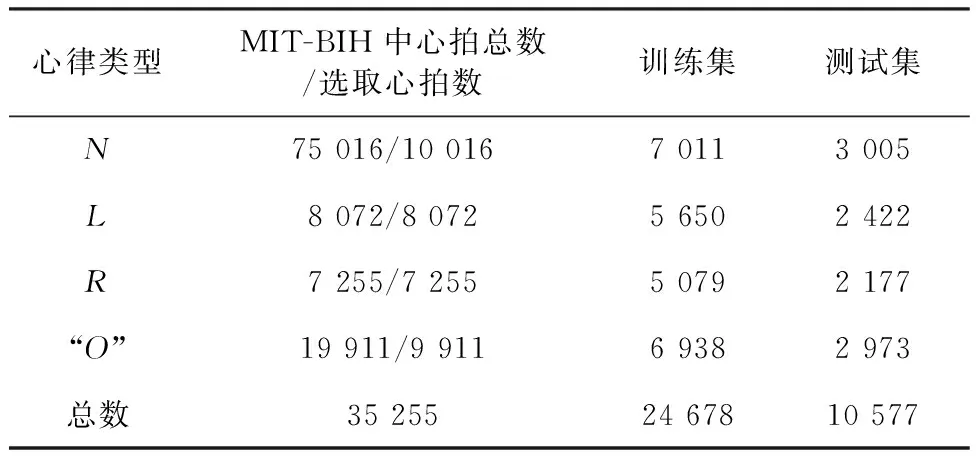
表1 MIT/BIH数据库中数据集划分

直接从MIT-BIH心律失常数据库中获取的原始ECG信号，存在电力线频率干扰、基线漂移、肌电图干扰等不可忽略的干扰因素，需要进行预处理.采用CWT对原始信号进行去噪[10]预处理，CWT的实质是对ECG原始信号的滤波，对于有限能量信号f(t),其基于母波Ψ的CWT可表示为

(WΨf)(a,b)=

(1)

其中,a∈R+为缩放因子；b∈R,为平移因子.本文选用墨西哥草帽函数为母波，其定义为

(2)

墨西哥草帽函数无限光滑即无穷次可微，因此它不对单独的噪声点敏感[11]，而其独特的时域特性，使得ECG信号的Q、R、S等特征点突出.由图2可以看出，图2(a)中ECG信号在处理前存在严重的基线漂移和一定的干扰. 图2(b)中处理后的ECG信号基与零纵轴对齐，ECG图像变得更加平滑,处理后的信号便于进一步处理和分析.

接下来，本文采用Pan和Tompkins提出的实时QRS波检测算法[12]来检测ECG信号中的QRS波.该算法对MIT/BIH异常心律数据的检测准确率达到99.3%.一个心拍周期的主要能量集中在QRS段，通过分割心拍可以去除冗余信息.检测到R峰值后，取R峰值前25点和R峰值后44点的数据，共70点数据片段代替一个心拍周期信号.

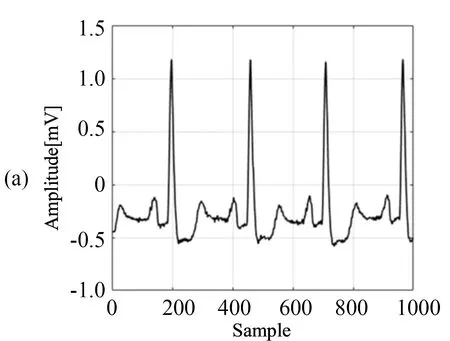
图2 原始ECG信号和预处理过ECG信号

2.2 特征提取

将ECG信号的特征从时域、频域和小波域中提取出来，从各个域获取信号特征，以便准确分类.

(1) 时域特征.不同类型的ECG信号在直观的波形上有一定的差异，可以从其波形中提取一些形态特征.对于每个信号段xn,其R峰振幅作为振幅特征.

Ampn=Max(xn)

(3)

每个信号段的标准差σn反映了信号在均值附近的波动程度.

(4)

其中,μ表示信号段均值.

峰值因子CFn表示峰值与有效值的比值.

(5)

其中,RMS(xn)表示信号段的均方根;peak(xn)是信号段的峰值.

形状因子SFn是一种受物体形状影响，但不受其维度影响的值.

(6)

其中,Mean(|xn|)是信号段的幅值均值.

脉冲因子IFn,其表示波形的冲击程度，对R波形的检测比较敏感.

(7)

(2) 频域特征.为了提取ECG信号的频域特征，首先对ECG信号进行快速离散傅里叶变换(Fast Fourier Transform, FFT).FFT是离散傅里叶变换(Design for Testability, DFT)的快速算法，对于ECG信号片段xn(i),i=1,2，…，70,其FFT可表示为

(8)

其中,WL=e-2πM,Xn(m)是ECG信号片段的频域表达式,其中m=1,2,…,L,表示谱线数.

在频域信息中,可以得到频率与幅值之间的关系.在频域中，QRS波位于高频区，而P波和T波位于低频区.不同类型的ECG信号在频率分量上存在较大差异.根据高频和低频的幅值差，选择了能够反映这些幅值差的一些特征.本文选取频谱均值、频谱标准差、频谱偏度和频谱峰度作为频域的4个特征.

频谱均值SMn为频率幅值谱的平均值.

(9)

频谱标准差SSDn表示信号在均值周围波动的程度.

(10)

频谱偏度SDn和频谱峭度SKn是从概率论和统计学角度定义的波形分布概率的描述式.

(11)

(12)

(3) 小波域特征.当被观测对象是具有多个动作电位的重复信号时，如ECG信号，小波域特征可以识别高频信号的相对分布[13].本文采用小波包分解(WPD)对ECG信号进行小波域分析.WPD是离散小波变换(DWT)的经典推广，它将频带划分为若干层，并对一般小波分析中未细分的高频部分进行分解.图3为三层小波包分解树示意图.S表示分解前的原始信号；A表示分解后的高频信号；D表示分解后的低频信号，脚标表示分解的层数.

图3 3层小波包分解树

本文选取“Shannon”熵类型，以“db6”为母波，对ECG信号进行四级分解[3].通过计算第四层小波包系数的奇异值、标准差和最大值[14]，可以得到三种小波域特征信息.由于第四层有16个频段，总共可以得到48个特征.设第四层分解得到的系数为ζ1,i=1,2,…,16.

奇异值SVDn反映了矩阵的固有特性，在信号处理、统计等领域有着重要的应用.奇异值具有良好的稳定性，它不会随着矩阵元素的微小变化而发生剧烈的变化.对于同一种ECG信号，其奇异值具有很高的相似性，很容易区分不同类型的心律.

SVDn=svd[ζ1,ζ2,...,ζ16]n

(13)

最大值MAXn是从第4层分解系数中直接选取的最大值.

MAXn=max[ζ1,ζ2,...,ζ16]n

(14)

标准差STDn来描述第4层分解系数的离散程度.

STDn=std[ζ1,ζ2,...,ζ16]n

(15)

综上所述，表2列出了从3个域中提取的所有特征.

表2从时域、频域、小波域提取的特征

Tab.2Allfeaturesextractedfromt-domain,f-domain,w-domain

特征种类特征名表达式时域特征幅值f1=Ampn标准差f2=σn峰值因子f3=CFn形状因子f4=SFn脉冲因子f5=IFn频域特征频率均值f6=SMn频率标准差f7=SSDn频率偏度f8=SDn频率峭度f9=SKn小波域特征奇异值f10～f15=SVDn最大值f16～f31=MAXn标准差f32～f57=STDn

特征值之间差异很大,如果将这些特征直接输入到经典算法中，算法的权值在收敛过程中会发生振荡，容易收敛到局部最优结果.为了避免这种情况，将采用以下方法进行归一化.

(16)

其中，j=1,2,3,…,57.处理后的特征值在-1～1范围内，这将大大提高学习算法的收敛能力.

2.4 GS-SVM

虽然SVM已成功地应用于ECG信号检测，但如何选择最优参数一直是一个难题.对于给定的训练集D={(x1,y1),(x2,y2),…,(xn,yn)},yi∈{-1，1}，i=1,2,3,…,n，其中,xn是输入,yn是对应的输出，SVM满足如下表达式[15-17].

subjecttoyi(wΤΨ(xi)+b)≥

1-ζi，ζi≥0.

(17)

其中,Ψ(xi)函数将xi映射到一个更高维的空间,C>0是误差项的惩罚因子.SVM目的是在高维空间中找到一个边界最大的线性划分超平面wTxi+b=0.在本文中,RBF核(k(xixk)=exp(-λ‖xi-xk‖2))作为核函数,其中，λ为核函数参数.对于整个算法，惩罚因子C和核函数参数λ的选取决定着算法的性能，为了获取最优参数，本文运用网格搜索法(GS)[18]来获取最优参数，可以同时对C与λ搜索，搜索过程中它们相互独立，能使算法达到全局最优.GS-SVM的流程如下所示.

步骤1:选择测试集与训练集.

步骤2:粗略选取能决定C与λ搜索范围的两个参数β∈[βmin，βmax]和ε∈[εmin，εmax]，β和ε为在各自固定步长下的取值.

步骤4:将SVM中C与λ参数设置为Pk，结合训练集对SVM进行训练，利用测试集输出得到分类正确率，将最高正确率对应的Pk记录下来.

步骤5:搜索结束时，如果最高正确率对应的Pk不落在由C与λ搜索范围组成的网格边界上，此时则得到了最优的C与λ，算法结束；否则要重新选定σ和ε，确保搜索结束时Pk落在网格边界内，回到步骤3.

混淆矩阵常用于表示分类的结果，从中可以知道有多少样品是正确分类的及一些其他的细节.表3为ECG信号分类的混淆矩阵.

表3 混淆矩阵

根据混淆矩阵，列出7个评价指标如表4所示，用来评估分类器性能.

表4 评价指标

3.2 仿真结果与分析

GS-SVM结合三域特征的ECG信号分类算法是在Matlab平台上实现的.利用训练集训练SVM分类器，通过测试集输出分类器的准确率，整个参数搜索过程可以用图4中的三维网格图表示.网格处的红点位置标记着最高分类准确率，同时也对应着最优的C与λ.

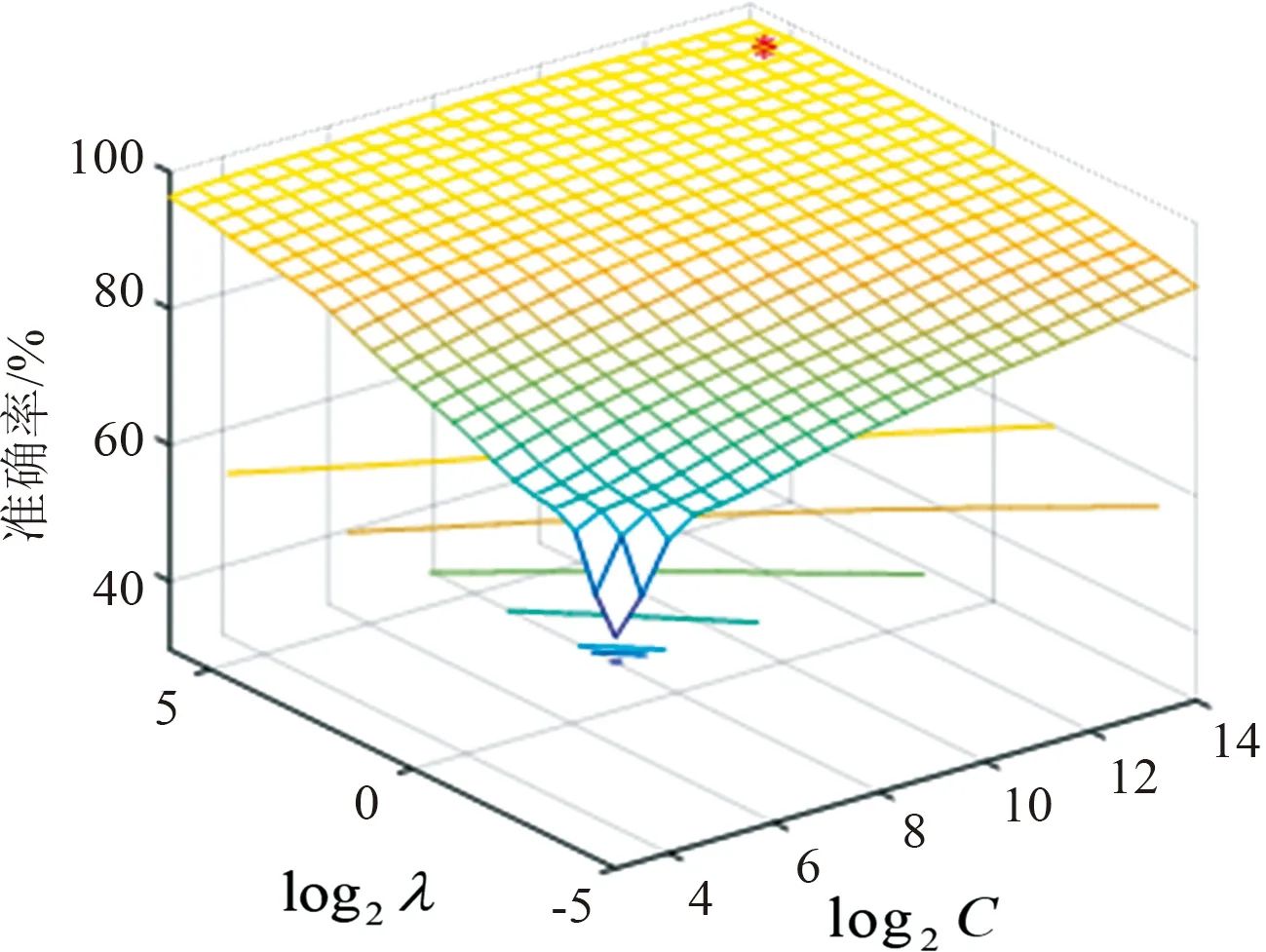
图4 搜索最优C与λ的三维网格

Fig.4 Three-dimensional grid graph of searching the optimalCandλ

为了探索不同域的特征对分类结果的影响，利用每一类特征、每两类特征和所有三类特征分别结合GS-SVM对ECG信号进行分类，以获得分类准确率和特征种类关系的折线图如图5所示,图中ft、ff、fw分别表示提取自时域、频域、小波域的特征.由折线图可知，如果仅利用一种特征来对ECG信号分类，小波域特征的效果最好，这是因为它对ECG信号的解释最为细致.时域特征有着最差的效果，这也解释着医生如果仅凭时域经验准则来分析ECG信号，结果可能会出现较大的偏差.但是对于分类器而言，时域信号对于提升ECG信号分类正确率还是有一定的帮助.

将测试集输入到最优参数配置的SVM中，得到表5所示的混淆矩阵.该矩阵详细的展示了4类ECG信号的分类情况.

图 5 三类特征对分类器的影响Fig.5 Effect of three types of features on classifier

表5提出的方法的混淆矩阵

Tab.5Confusionmatrixofproposedmethod

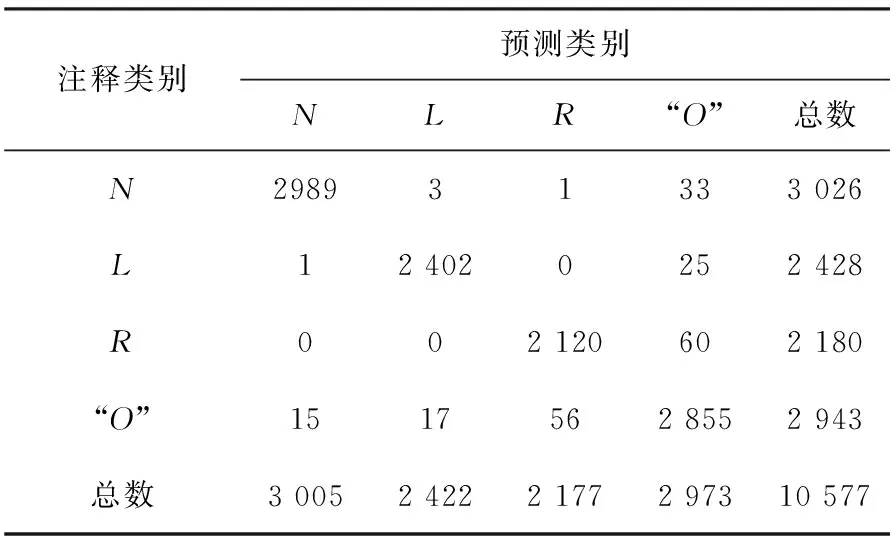
注释类别预测类别NLR“O”总数N298931333 026L12 4020252 428R002 120602 180“O”1517562 8552 943总数3 0052 4222 1772 97310 577

基于混淆矩阵，计算各性能评价参数如表6所示.SPC、REC、PRE、NPV分别表示每一种ECG信号的分类效果，例如REC表示该种信号TP的占有率，也表示其召回率.OA、OE和F1分数是分类器的总体评价，例如F1分数是REC和PRE的调和平均值，越接近1，就表示分类器效果越好.

表 6 每个类别的性能评估

3.3 结果比较

表7给出了本文方法与其他文献中方法的ECG信号分类结果对比.在文献[7]中，用主成分分析(PCA)和核独立成分分析(KICA)特征提取ECG信号特征，再采用基于遗传算法优化的SVM算法(GA-SVM)将ECG信号分为了5类，其准确率为97.78%，但样本仅为720个心拍；在文献[2]中，用Hermit函数对ECG信号进行变换，提取系数再结合一些时域特征作为总的特征，利用基于粒子群算法优化的块神经网络(PSO-BBNN)，将ECG信号分为5类，分类正确率为97%；在文献[19,20]中,提取了ECG信号的时间域波形间隔特征和纹理特征，利用基于遗传蝙蝠优化算法的支持向量神经网络(GB-SVNN)，将ECG信号分为心律失常或无心律失常信号，其准确率为96.96%；在文献[1]中，从ECG信号中提取了高阶谱(HOS)特征，然后经过PCA降维，最后利用最小二乘支持向量机(LS-SVM)将ECG信号分为5类，准确率为93.48%；在文献[6]中,利用WPD结合统计方法提取特征，利用基于遗传算法的BP神经网络(GA-BPNN)将ECG信号分为了6类，得到了97.78%的正确率，但仿真中仅用到300个实验数据. 在文献[20]中，研究了三种监督分类算法，多层感知器(MLP),SVM以及径向基函数和概率神经网络(RBFNN，PNN)对ECG信号分类的效果，结合基于形态学和时间序列的时域特征，将ECG信号分为3类，分类精度最高为97.14%.其中，文献[6-7]里的实验数据不够多，得到的分类器不能认为具有较好的泛化能力和鲁棒性.本文提出的方法对ECG信号三域特征进行了研究，利用GS-SVM对MIT/BIH中48个文件的ECG信号分类，得到准确率为98.02%，该方法取得较高的准确性，较多的实验数据也保证了分类器的泛化能力和鲁棒性.

表7 与其他文献结果对比

4 结 论

本文提出了一种基于三域特征提取和GS-SVM的ECG信号检测方法.时域特征是ECG信号基于时间序列的形态学描述；频域特征描述ECG信号的频率统计学特征；小波域特征是低频和高频中没有反映出来的细节信息.ECG信号可被这些特征充分地表示，将GS-SVM与这些特征相结合，实现了ECG信号的智能分类，该方法可以有效地帮助医生对患者进行诊断.