基于蒙特卡罗算法的高温作业防护服优化设计

王 丽 燕， 李 庆 杰， 李 雁 宙， 冯 丹 亭， 严 潇， 蔡 方 赟

( 1.大连大学 信息工程学院, 辽宁 大连 116622；2.大连大学 环境与化学工程学院, 辽宁 大连 116622 )

0 引 言

随着社会的发展，越来越多的工作需要在高温环境下完成，而高温作业带有极高的危险性．在高温环境下工作时，人们需要穿着专用的高温作业防护服，才能避免高温灼热带来的伤害．卢琳珍[1]基于非线性变系数抛物型方程，建立了多层热防护服-空气层-皮肤系统的热传递模型，利用有限差分法对所建模型进行了收敛性分析，给出了各层接触面之间的关系．但该系统仅停留在理论研究层面，没有进一步运用到服装设计上．陈柔羲[2]从人体热湿生理和运动需求出发，对PCM(相变材料)在高温防护服内的分布情况进行了优化设计，并依据热湿舒适性对模型进行了改进．但所选取的样本数比较少，试验结果具有偶然性．Ghazy等[3]通过建立一个瞬态传热有限体积模型，研究了防护服系统的瞬态温度分布和能量含量，但忽略了防护服中空气间隙对防护服性能的影响．毛瑶瑶等[4]在温度和时间的约束条件下，利用遗传算法求出了防护服第2层的最优厚度，但遗传算法不能及时利用网络的反馈信息，计算效率较低．本文围绕2018年全国大学生数学建模竞赛A题“高温作业专用服装设计”(http://www.mcm.edu.cn/html_cn/node/7cec7725b9a0ea07b4dfd175e8042c33.html)，在降低研发成本的条件下，对高温作业专用服装的厚度进行优化求解．所研究的高温作业专用服装由3层织物材料构成，其中第1层与外界环境接触，第3层与皮肤之间还存在空隙，将此空隙记为第4层．利用蒙特卡罗算法求解防护服第2层与第4层的最优厚度．在求解过程中，不仅考虑到空气间隙对防护服性能的影响，而且在全局随机取样，避免陷入局部最优解．

1 防护服温度分布的求解

由文献[5]可知，当皮肤外侧的温度不再改变时，整个系统达到稳态，即物体各点的温度不再随时间变动，而之前时间段皮肤外侧传热过程均为非稳态导热过程．因此，在求解关系式的过程中，要考虑至少两个状态下的导热情况．以后的所有分析都基于这一前提．本章通过求解热传导偏微分方程[5]，建立离散型热传导模型，对高温作业防护服仿真设计，求解每一层的温度分布．

1.1 热传导方程离散化

将高温作业防护服进行一维切片化处理后得到高温作业防护服热传导示意图，如图1所示．

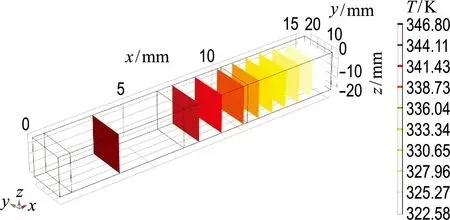
图1 高温作业防护服热传导三维等温示意图

Fig.1 Three-dimensional isothermal diagram of heat conduction of high-temperature operation protective clothing

从图1可以直观看出温度的传导方向和传导过程．热传导方程式[6]如下：

(1)

其中ρ、Cρ均为常数，由于每一层的热传导率不同且是离散的，式(1)中k值不是常数．对热传导方程(1)进行离散化处理，离散化处理过程如图2所示．

图2 离散化处理示意图

图中的Δx和Δt分别表示厚度的步长和时间的步长．i表示离散点的厚度轴坐标，j表示离散点的时间轴坐标．则由式(1)可得

(2)

(3)

将式(2)、(3)同时代入热传导方程(1)中，得到离散化的热传导方程为

(4)

在将偏微分方程(1)离散化处理之前，应先设置初值，即各层防护服在t=0时均为一常数值，初值设立如下：

T1(x，0)=348

(5)

T2(x，0)=310

(6)

T3(x，0)=310

(7)

T4(x，0)=310

(8)

在求解过程中，经过离散化热传导方程的不断迭代，可得到每一层的、每一时间点上的各个温度值．

1.2 防护服各层温度分布的求解

分别将密度、比热容、热传导率、环境温度和假人外表皮温度代入式(4)中．假设横轴达到0.6 mm 时作为第1层，横轴为0.6～6.6 mm时作为第2层，横轴为6.6～10.2 mm时作为第3层，横轴为10.2～15.2 mm时作为第4层．用MATLAB求解式(4)，可得到每一层材料各处的温度值．

在此基础上，基于得到的每一层材料各处、各时间点对应的温度值，找出相邻两层之间不同时间点对应的温度值并作图，即得到每两层间温度随时间变化的二维平面图，如图3所示．

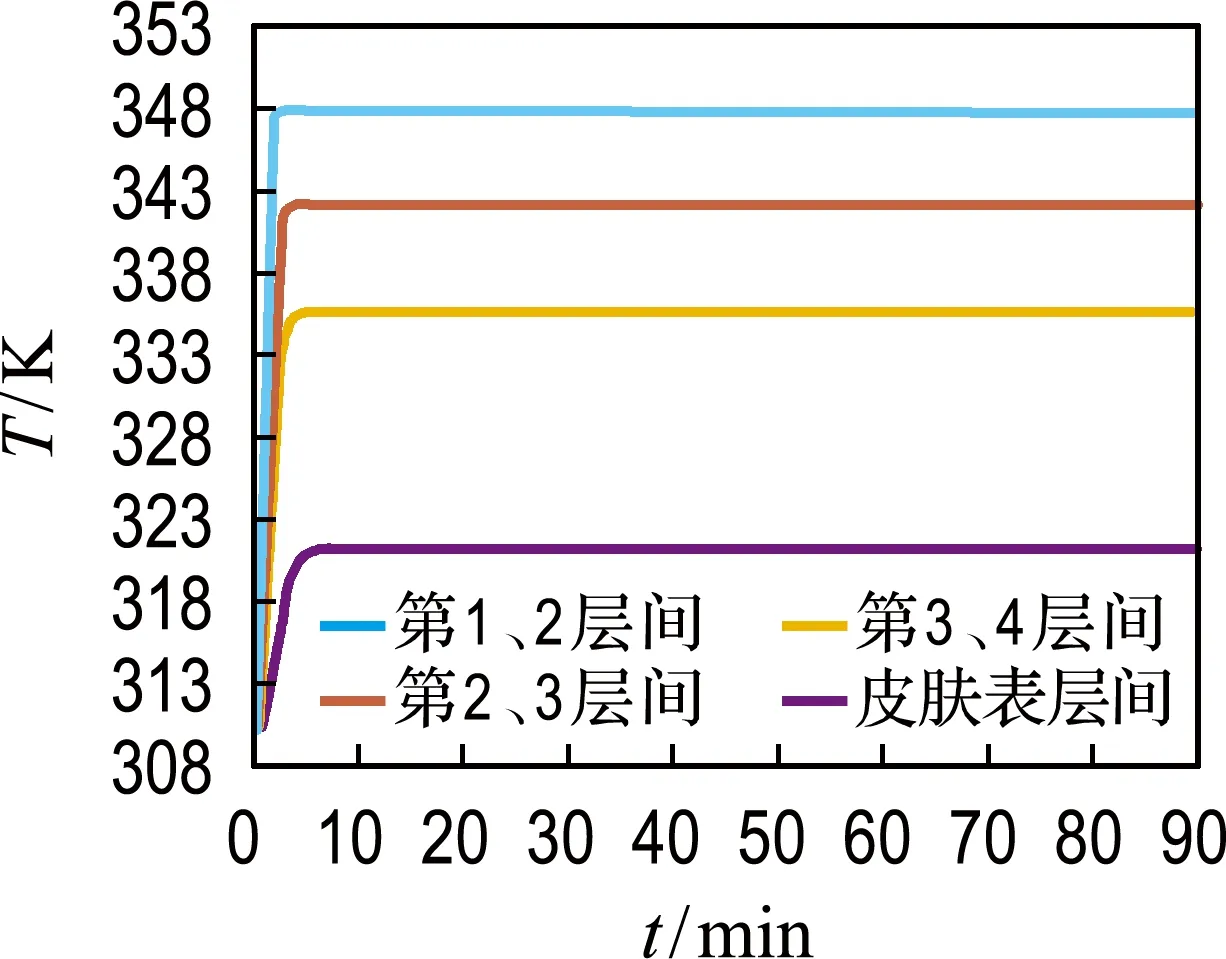
图3 每一层温度随时间变化的分布示意图

从图3中可以看出：温度从第1层开始到第4层，先后逐渐趋于稳态，并且在传递热量的过程中，能量被损耗，最终使得热量的传递值递减，每层的稳态温度都低于其上一层．为方便看出各层处于稳态时的温度，做出5 400 s时的各层温度情况，如图4所示．

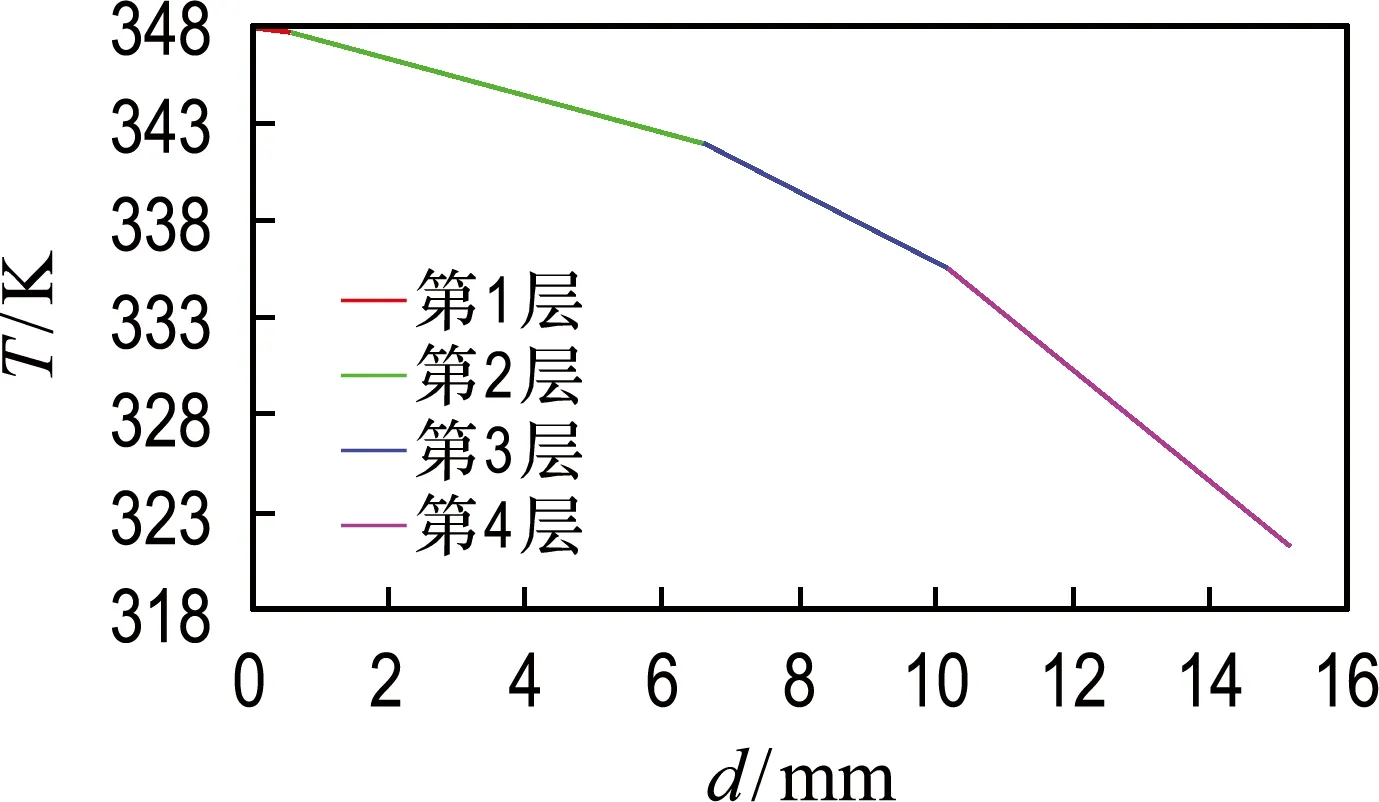
图4 各层达到稳态时的温度分布情况图

由图4可以看出，第4层空气层温度下降最多，说明空气层对人体隔热防护更为重要．

1.3 误差分析

将各层温度数据代入均方根误差[7]公式：

(9)

对温度分布结果进行分析．把用MATLAB计算得出的温度分布值与测量得到的真实值进行对比，得到表1．

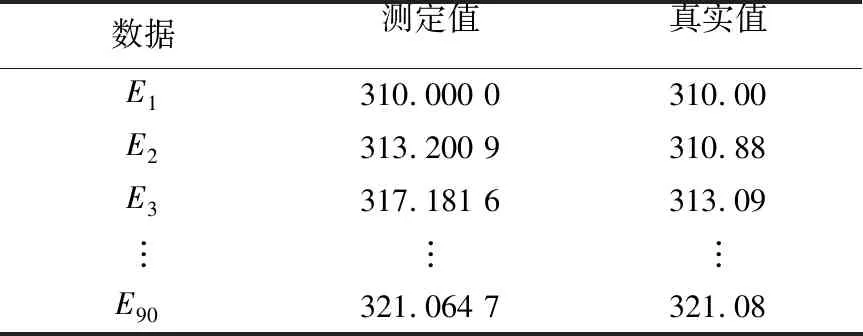
表1 误差分析表

由此得出均方差σ=1.021 0，误差较小．因此，本文所建立的温度分布模型合理、可行．

2 基于蒙特卡罗算法求解防护服最优厚度

求解最优厚度的方法有很多，例如穷举法、模拟退火、遗传算法等．穷举法虽然方法简单，但是实施起来过于繁琐复杂；启发式算法虽然常用，但是容易陷入局部最优解．对于本文所研究的最优厚度求解来说，蒙特卡罗算法不仅方法简单，而且在求解过程中，通过随机投点，可以避免陷入局部最优解，使结论更具有说服力．因此，本文采用蒙特卡罗算法，求解防护服的最优厚度．

假设边界空气层温度T0=353 K，假人皮肤外侧温度约束条件有

(10)

在满足约束条件的情况下，为了降低研发成本和缩短研发周期，服装的总厚度值应该最小，即

min(d)=min(d1+d2+d3+d4)

(11)

根据蒙特卡罗算法，将厚度进行随机投点，则由d2和d4生成n个随机数(其中d2的范围为0.6～25 mm，d4的范围为0.6～6.4 mm)，代入式(4)并求出其温度分布．在满足约束条件的情况下，随着每次d2和d4数值的改变，会生成不同的目标函数，同时记录当前最优解．当投点次数n取100，101，102，103，104，…时得到材料厚度收敛图，如图5所示．

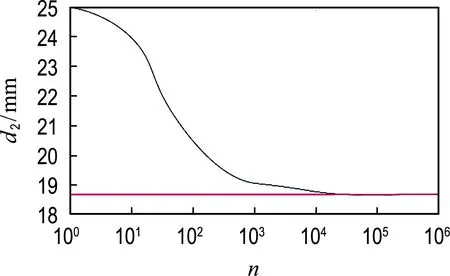
(a) 第2层

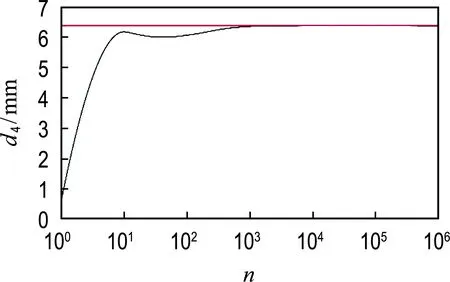
(b) 第4层

图5 厚度收敛图像

Fig.5 Thickness convergence image

当t=1 800 s时，温度不断向320 K逼近；当t=1 500 s时，温度不断向317 K逼近．第2层和第4层厚度随时间变化不断向最优厚度收敛，此时可以得到第2层的最优厚度值收敛于18.68 mm左右，第4层的最优厚度值收敛于6.4 mm左右．

由于蒙特卡罗算法生成的随机数带有一定的随机性，每次的结果都具有一定的误差，本文选择多次测量取平均值的方法，确定最终的最优厚度．而上文所提到的投点次数n的选取会严重影响代码的计算时间，在保证准确性并且缩短计算时间的前提下，经过多次试验，当选取投点次数n为1×106时，各提取一组样本(共7个)如表2、3所示．

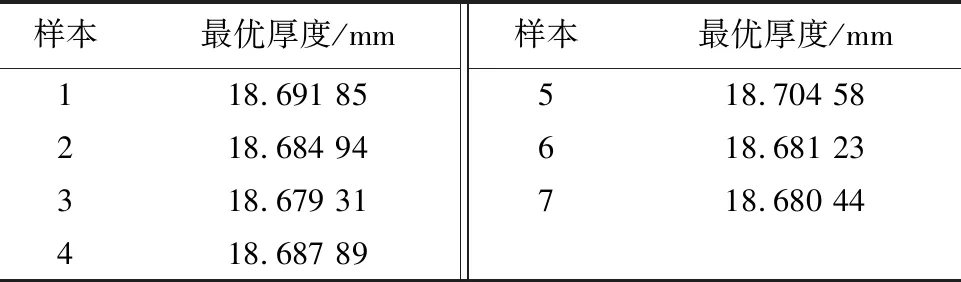
表2 迭代次数为1×106时第2层的厚度

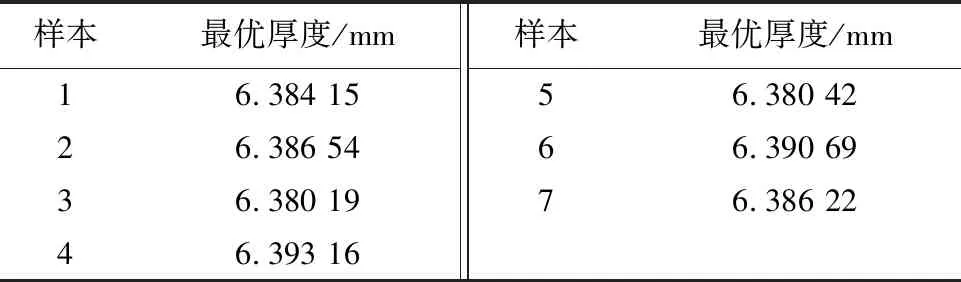
表3 迭代次数为1×106时第4层的厚度

将样本中的最优厚度求算术平均值，计算得出第2层的最优厚度为18.68 mm，第4层的最优厚度为6.38 mm．此时满足当边界空气层温度为353 K 时，确保假人皮肤外侧温度在工作30 min时，不超过320 K，且超过317 K的时间不超过5 min．

3 结 语

在利用傅里叶热传导定律求解防护服各层的温度分布时，由于每一层的热传导率不同且是离散的，本文通过稳态热传导方程、传热学原理等构建了一维稳态热传导模型．利用有限差分法求解出人体皮肤外侧每一层织物材料的温度分布情况，对所求得的结果进行了误差分析，验证了模型的可靠性．并基于以上模型，对防护服第2层与第4层的最优厚度进行了求解．借助MATLAB软件，运用蒙特卡罗算法，先对厚度值进行不同次数的随机模拟取点，在满足约束条件的情况下，求解出不同次数下对应的厚度值，然后对厚度值进行收敛分析，发现当投点次数为1×106时，收敛曲线趋于平滑，此时计算结果精确度较高，计算时间较短．由于蒙特卡罗算法获得的结果具有一定的随机性，在投点次数为1×106的条件下获得7组样本数据，然后通过样本均值排除误差，得到防护服第2层与第4层的最优厚度．此时的最优厚度为防护服满足约束条件下的最小值，降低了研发成本，缩短了研发周期．但是为了方便求解，没有考虑人体皮肤表面的汗液、水汽等因素的影响，因此，模型还有较大的优化空间．但可为相关高温热防护服设计及其衍生产业发展提供一定的参考．