数词逻辑意义与语用意义的儿童习得 *

范 莉

(中央财经大学，北京 100081)

提 要：本研究以数词的意义解读为切入点，讨论会话隐含产生的缘由，逻辑意义与语用意义的关系。研究对以普通话为母语的39名3-6岁儿童和12名成人进行测试，测试结果表明：确切数字解读是数词意义的根本，是语义解读，它相对独立于语境，对语境信息量的要求低，易于计算，是儿童较早获得的解读；“至少”解读和“最多”解读是语用解读，对语境信息的依赖性较强，计算较复杂，是儿童较晚获得的解读；相对缺省论而言，关联论关于逻辑意义与语用意义关系的假设更符合语言习得的事实。

1 研究缘起

数词意义的解读具有多样性、复杂性，与逻辑意义和语用意义相关。以一个故事为例：

“小狗在森林里玩，遇到了仙女姐姐。仙女姐姐拿出了一个口袋，里面有漂亮的石头。仙女姐姐说“小狗，我的石头很漂亮。不多了，我想自己留着。你拿两块吧。”若脱离故事语境，含有数词“两”的句子可有以下解读：(1)确切数字解读(exact number reading)：小狗可以拿正好两块石头；(2)“至少”解读(at-least reading)：小狗可以至少拿两块石头。(也即是：小狗可以拿两块石头，或者拿更多的石头。)(3)“最多”解读(at-most reading)：小狗可以最多拿两块石头。(也即是：小狗可以拿两块石头，或者拿一块石头，又或者一块石头都不拿。)

在这3种解读中，哪种属于逻辑语义的解释，哪种属于语用隐含的解释，哪种是数词意义诠释的根本？对这些问题的思考引发我们对会话隐涵的起因、逻辑意义与语用意义关系等的思考。

2 理论讨论

2.1 会话隐含的产生

一个话语有“字面之意”(what is said)，也可能有“言外之意”(what is implicated)。根据Grice(1989:30)，说话人对合作原则和其准则的公然违反使得话语具有语用的扩充意义，激活会话隐含。听者可凭借以下信息获取会话隐含(Conversational Implicature)：所使用的词语的规约意义以及指称对象；合作原则及其准则；语言背景，或其它背景信息；上述内容都是谈话双方能获得的，并且双方都假定为真的(同上:31)。

2.2 逻辑意义与语用意义的关系

Grice(同上:25)认为，词语的规约意义(conventional meaning)有助于确定话语能表达的字面意义，此外还决定其能隐含的言外之意。也就是说，规约意义，即逻辑意义，是语用扩充意义产生的基础；语用意义的激活依赖语境。规约意义和隐含意义无法完全剥离开。有些隐含意义是规约的；会话隐含是非规约隐含的一个子集(同上:26)。

继Grice后，就隐含的由来，逻辑意义与语用意义的关系等出现不同的看法，大致可分为：缺省论(Levinson 2000, Chierchia 2004)和关联论(Sperber，Wilson 1986)。 根据缺省论，语用意义是缺省的，将其中与语境信息兼容的扩充意义剥离出来才得到逻辑意义。Levinson(2000)界定3个层次的意义：句子—类型意义(sentence-type meaning)、话语—标志意义(utterance-token meaning)和话语类型意义(utterance-type meaning)。其中的最后层次即是一般会话隐含(Generalised Conversational Implicature)。Levinson (同上:1)认为，一般会话隐含是源于话语结构，而非话语特定的语境。Chierchia(2004:40)提出，语用意义的计算和语法驱动的语义意义的计算是穿插(intersperse)进行的，并不是在句子的真值条件确定后才启动对隐含的计算；因此，隐含的计算是逐个短语，与真值计算同时进行。层级隐含是在局部产生，然后以反映标准语义递推的方式向更高的语言层级投射。以上论述的核心思想之一就是，语用意义的计算对语境信息并不具有加强的依赖性，并且其计算的可行性并非以逻辑意义的计算结果为前提。

根据关联论(Relevance Theory)，依据语境，语用意义是在满足对相关性期待的前提下将逻辑意义扩充而得。据此，话语的解读要经历3个可能的阶段或层次：首先，对不完整的逻辑形式进行恢复；接着，使这些逻辑形式扩展或完整以产生字面意义(explicatures)；最后，派生出言外之意，即隐含(implicature)。字面意义和隐含意义的产生都是受到关联原则的驱动，即从对认知的影响和处理所需投入之间实现平衡，寻求最佳的解读(Sperber, Wilson 1986:47-50)。一旦听者发现一种解读符合关联的标准，就可以认为这个解读是说话者要表达的信息。根据缺省论和关联论的假设，就逻辑意义与隐含意义的性质、计算复杂度，以及习得难度的推测等问题，总结为表1。两种不同的意义计算和习得模式，孰正孰误？

表1 缺省论和关联论的相关推测

2.3 数字解读的性质

有一种分析为：确切数字解读是语义解读，是数字最基本的解读；“最多”解读和“至少”解读是依赖于语境信息所产生的扩充性解读。Horn(1972)却提出“至少”解读是语义解释；确切数字解读是根据Grice(1975)提出的合作原则(Coo-perative Principle)中的数量准则(Quantity Maxim)推导出来的，属于语用解释。于是再问：两种不同的分析，孰正孰误？

3 研究问题

语言实验有助于加深我们对逻辑意义与语用意义间关系、数词解读性质的认识。不过，目前实证研究还存在以下问题：第一，实验结果存在冲突：支持缺省论的，有Slabakova(2010)；支持关联论的有Smith(1980)、Musolino和Lidz(2002)、Noveck(2001)、Papafragou和Musolino(2003)。缺乏一致的实证材料的支持，两个理论间的冲突难解难断。第二，实验设计不够完善。主要体现为：相同设计得出不同结果。如Breheny等(2006)复制Bezuidenhout和Cutting(2002)的实验，却得出相反发现。同类研究对象带来不同结果。如均是就外语学习者的研究，Takahashi和Roitblat(1994)的报告则与Slabakova(2010)的存在冲突。第三，目标语不丰富，汉语研究缺乏。主要是英语语料的研究无法支撑任何具有跨语言普遍性的假设。第四，实验语用学在我国仍处于渐进发展阶段，有一些介绍性的文献(方传余 2006，刘思 2008)和实验研究，但联系重大语用理论争议的研究还须加强。

鉴于研究现状，我们的研究围绕这些课题展开：第一，语境因素：不同语境信息量对数词解读的影响。设置语境信息丰富与不丰富两种测试背景，考察语境信息量的差异是否会给成人和儿童对数词解读带来影响，并且讨论由此产生的不同解读的性质。第二，解读性质：同一测试语境中不同解读的接受度差异。第三，年龄变量：同一测试语境中，不同年龄被试对同一解读判断的异同。考察各组被试对数词各种解读的接受情况，分析儿童与成人判断的差异，呈现相关知识随着年龄增加日益成熟的过程。第四，句法影响：同一语境，不同句法结构对被试判断的影响。总结研究所涉及的变量，即：不同的语境、不同的解读、不同的年龄以及不同的句法结构。

4 研究设计

4.1 测试对象

被试含39名儿童和15名成人。年龄组、人数、年龄段与平均年龄的信息是：3-4岁组，12人，2;7-3;9①，3;3。4-5岁组，12人，4;0-4;7，4;3。5-6岁组，15人，4;8-5;7，5;2。成人组，15人。

4.2 测试材料

根据汉语的特点，结合已有的研究成果，在测试结构的设计上，我们考虑到以下因素：

第一，数词短语作主语时，前面有无“有”是否会引起解读差异。数词短语在汉语中是否可以直接作主语，一直存在争论，因此在测试结构的设计上关注作主语的数词结构的构成也就很有意义。

第二，数词短语的句法位置是否会产生解读差异。句法位置有可能会对语义解读造成影响，所以我们测试数词短语分别处于主语和宾语位置的两种结构。

第三，语境的信息量是否会影响数词的解读。根据语境信息量的多少，我们的测试内容分为语境丰富和语境不丰富的两类。在语境信息不丰富的测试中，除了图片信息外，被试获得的语言信息只有测试句或测试问题。这类测试的形式包括两种：根据图片判断句子正误和根据问题选择图片。语境丰富部分的测试是指给被试提供一个短小的测试故事，然后要求被试根据测试故事回答问题。测试方法和测试结构的具体信息如下：

测试方法(1)：向被试展示图片，然后要求根据图片内容判断测试句是否准确描述图片。如是，答“对”；否则，答“不对”。

表2 图片判断测试中结构的信息②

测试方法(2)：向被试展示每组图片，告知被试每组图片共有3张，其中一张上画有内容，但是被遮挡住。每组图片给被试一个测试问题，被试被告知其中一张图片能用来回答问题。

表3 图片选择测试中测试内容和结构的信息

测试方法(3)：将测试故事做成动画，由笔记本电脑播放。要求被试看完故事后，根据故事内容回答问题。

表4 “看故事，答问题”测试中测试内容和结构的信息

具体例子如下：

① 测试目的：测试数词取“最多”解读、假设答案为肯定答案时，被试的判断。

测试故事：小狗在森林里玩，遇到了仙女姐姐。仙女姐姐拿出了一个口袋，里面有漂亮的石头。仙女姐姐说“小狗，我的石头很漂亮。不多了，我想自己留着。你拿2块吧。”

测试问题：小狗可以拿1块石头吗？

② 测试目的：测试数词取“至少”解读、假设答案为否定答案时，被试的判断。

测试故事：老师对小兔子说“明天我们做蛋糕。做蛋糕要用2个鸡蛋。小兔子，你拿2个鸡蛋吧。”

测试问题：小兔子可以拿1个鸡蛋吗？

5 结果和讨论

5.1 语境不丰富条件下的测试

5.11 真值判断测试

测试结果显示，无论主语位置上的数词短语前有无“有”，儿童组与成人组对确切数字解读的判断不存在显著性差异(z<1.96, p>0.05)。当测试图片呈现确切数字解读时，被试都给出肯定答复；当测试图片呈现的不是确切数字解读时，只有个别的被试给出肯定答复。当测试图片呈现的是数词的“至少”解读时，5-6岁组的判断与成人组存在显著性差异(z=-2.143, p<0.05)，但5-6岁组与4-5岁组的判读不存在显著性差异(z=-1.12, p>0.05)。③

表5 真值判断测试：数词短语作主语的句子

当数词短语充当宾语时，儿童与成人对确切数字解读、“至少”解读的判断都不存在差异。其中，在对“至少”解读的判断时，5-6岁组与成人组的统计分析结果是：z=1.6, p>0.05。

表6 真值判断测试：数词短语作宾语的句子

5.12 图片选择测试

图片选择的测试题根据确切解读是否被遮挡的图片而分为两种。在第一种的测试中，属于无关项的图片被遮挡，呈现确切数字解读和“至少”解读的图片未被遮挡。测试结果表明，所有的被试都选择呈现确切解读的图片。

在第二种的测试中，被试所能看到的是呈现“至少”解读、和无关解读的两张图片，因此被遮挡的图片就可能呈现确切解读。各测试组中，绝大多数的被试都选择了被遮挡的图片。只有3-4岁的儿童与成人存在显著性差异(z=3.4, p<0.05)。与成人的判断相比，5-6岁儿童的表现虽比4-5岁儿童的差，但是5-6岁儿童的判断与成人不存在显著性差异(z=1.011, p>0.05)。当有可能是呈现确切解读的图片被遮挡时，3-4岁组无被试接受“至少”解读，而4-5岁组、5-6岁组和成人组都有少数被试接受这种解读，并与成人的判断不存在显著性差异。其中5-6岁儿童与成人的判断差异的z检验结果为z=1.047, p>0.05。具体的统计数据如下表。

表7 图片选择测试：确切数字解读图片在被显示和被遮挡的条件下

在语境不丰富的测试条件下，各组被试根据图片进行真值判断和选择图片回答问题的测试结果反映出：第一，数字的确切解读是数词意义的根本，是基本独立于语境的。相比之下，“至少”解读在语境信息不丰富的情况下很难被激活。无论数词作主语时前面有无“有”，均不会影响成人和儿童对数词解读的判断。此外，数词短语是出现在主语位置还是宾语位置对被试的判断基本没有影响，确切数字解读几乎是成人和儿童接受的唯一解读，仅有极少部分成人和儿童接受“至少”解读。第二，“至少”解读是可能的，却是边缘性的。当语境信息不丰富的情况下，在对确切数字解读、“至少”解读和无关解读进行选择，确切数字解读在两种测试情况下都是绝对优选的解读。只有当所展现的图片是“至少”解读和无关解读时，才有少数被试接受“至少”解读。第三，3-4岁儿童表现出对确切数字解读的强烈偏爱，他们对此解读的判断已与成人已无显著性差异。在语境信息不丰富的测试条件下，4-5岁儿童对“至少”解读的判断也与成人不存显著性差异。

5.2 语境丰富条件下的测试

在语境丰富的情况下，我们测试被试对“最多”解读和“至少”解读分别在可成立和不可成立两种真值条件下的判断。

当测试故事包含的真值条件使“最多”解读为真时，几乎所有的成人都接受“最多”解读。这说明，“最多”解读在有语境的情况下可以被激活。从儿童到成人语言发展的角度来看，5-6岁儿童与成人的判断存在显著性差异(z=2.53, p<0.05)，儿童给出否定回答的理由是，故事中的数词应取确切数字解读。当故事包含的真值条件使“最多”解读为假时，各组儿童与成人的判断表面上与测试假设相符合，但是当深究他们给予否定回答的原因时，发现儿童如此判断的理由还是因为他们赋予数词以确切解读。有少数成人给予肯定的答复，从他们给出的理由来看，是因为他们认为说话人在说如“你拿N个吧”这样的句子时约束力并不强，因此数词的解读可以任由听话人来决定。在这个测试内容中，成人组与各个儿童组均存在显著性差异(其中，5-6岁组儿童与成人的判断差别是：z=2.57, p<0.05)。

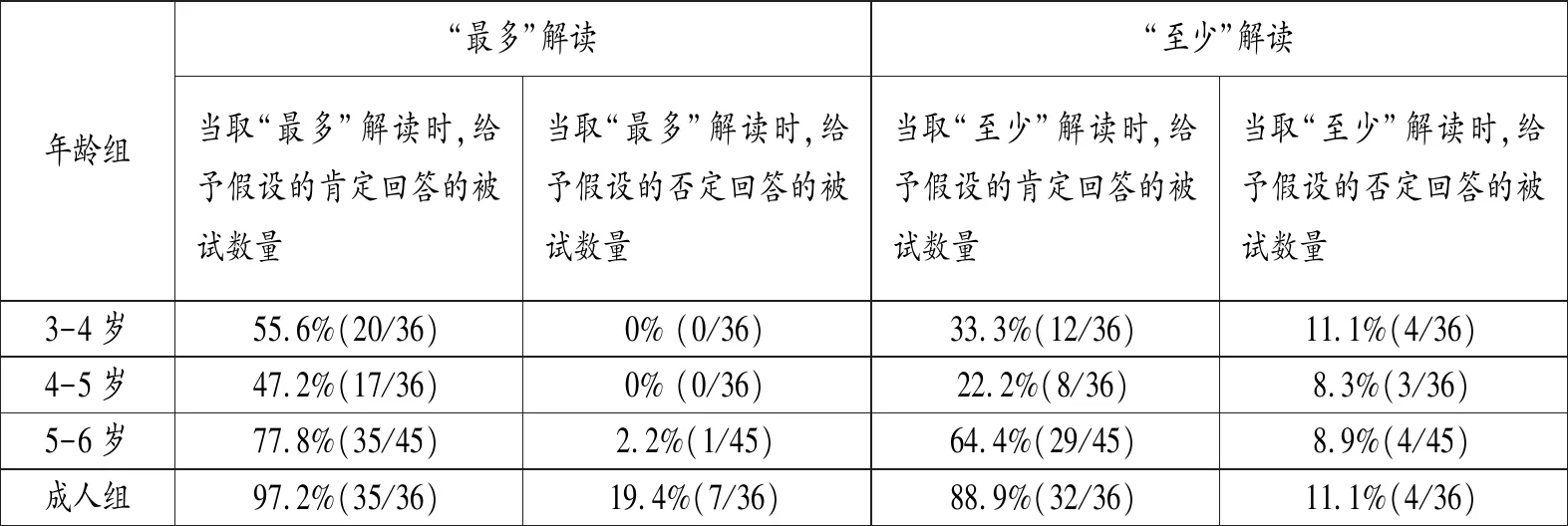
表8 “看故事，答问题”测试：“最多”解读和“至少”解读的测试

在“至少”解读假定为真的情况下，特别是低年龄段的儿童表现出赋予数词确切数字解读的趋势，于是对测试问题做出否定的判断。从发展的角度来看，5-6岁的儿童与成人进行判断时还存在显著性差异(z=2.52, p<0.05)。在“至少”解读假定为假的情况下，各组儿童与成人的判断都不存在显著性差异。

表9 “看故事，答问题”测试：“至少”解读的测试

5.3 “至少”解读在两种语境条件下的测试结果

当“至少”解读假定为真，在语境丰富(根据故事回答问题测试)与不丰富(图片判断测试)的两种测试条件下，除了4-5岁组，其他各组儿童与成人在不同语境条件下的判断都存在显著性差异。这证明，“至少”解读只能在语境丰富的情况下才能被激活。各组具体配对样本t检验的数据见表10：

表10 “至少”解读在语境丰富和不丰富两种条件下的测试结果对比

6 研究结论

6.1 数词短语各种可能解读的性质

在语境信息不丰富的情况下，无论数词短语是出现在主语位置还是宾语位置，儿童与成人几乎全部接受确切数字解读。有少部分成人接受“至少”解读，5-6岁儿童与成人在这点上仍存在显著性差异。当获取较多语境信息后，3-4岁组就有儿童接受“至少”解读和“最多”解读，不过5-6岁组儿童与成人的判断仍存在显著性差异。

Horn(1972:38)提出“至少”是语义解释，而确切数字解读则是从Grice准则中推导而来的。但测试结果则反应出不同的性质：确切数字解读是相对独立于语境的，对语境信息量的要求低，易于计算，是数词意义的根本，是语义解读，是儿童较早获得的解读。就像儿童在1岁开始咿呀学语，接触数字时，成人通常引导儿童将数字与具体的物体进行逐一匹配地数数。也就是说，对于儿童来说，关于数词意义解读的初始状态就是确切解读。“至少”解读和“最多”解读对语境信息的依赖性较强，计算较复杂，是语用解读，是儿童较晚获得的解读。

6.2 数词短语各种解读的优选性

在语境不丰富的条件下，儿童和成人在进行真值判断和图片选择的测试中都表现出对确切数字解读的强烈偏爱。即使在语境信息丰富的条件下，儿童判断“最多”解读和“至少”解读是给出与测试假设不一样的答案，也是因为他们仍然将数词进行确切解读。在同样测试条件下，成人相比之下表现出对确切数字解读不是那么坚持。这也进一步支撑了关于儿童比成人更具有逻辑性的假设(Noveck 2001:165)，也就如在处理结构歧义时，儿童就无法完成各种涉及语用推测的任务(Trueswell et al. 1999)。

6.3 数词短语各种解读的早期习得

关于数字意义完整知识的发展是一个渐进的过程。3-4岁儿童关于确切数字解读的判断已与成人无显著性差异，但是5-6岁儿童对“最多”解读和“至少”解读的判断与成人还存在显著性差异。“最多”解读涉及层级隐含(Hirschberg 1985; Sperber，Wilson 1995; Levinson 2000)，它在儿童早期语言发展中的延迟习得也证明：儿童相对成人来说较少地生成等级隐含(Chierchia et al. 2001; Noveck 2001; Papafragou, Musolino 2003; Huang, Snedeker 2009; Foppolo et al. 2012).

6.4 “关联论”关于意义计算和习得过程假设的合理性

数词解读的测试结果总结为表11，并与表1中关于“缺省论”和“关联论”的假设比较，我们得出的结论是：关联论关于逻辑意义和语用意义产生关系的假设是正确的，即逻辑意义是语用意义的基础，后者是由前者加上语境信息推导而出的。

表11 数词解读的测试结果

注释

①此处儿童年龄表示的格式为：(岁);(月)，如2;7即是：2岁7个月。

②每个情况下，包含数词“二”“三”“四”的测试句各一个。在每种测试正式开始之前，都有预备项目，以帮助被试熟悉测试环节。

③在两类结构的测试中，都有个别成人的判断与测试假设有出入，应该是对图片理解出现偏差所致。