各向异性磁弹性传感器及其线性度拟合直线研究

刘晓蒙，张怀锁

(上海工业自动化仪表研究院有限公司，上海 200233)

0 引言

物质在磁场中被磁化时，其尺寸或外形发生变化的现象称为磁致伸缩现象[1]。1865年，维拉里(E.Villari)发现铁磁性物质发生变形或在应力的作用下，其磁通会发生变化。这种变化被称为维拉里效应。利用维拉里效应制成的压力传感器称为磁弹性传感器。

对于传感器的输出，人们总是希望与传感器输入有明确对应的线性关系。实际上，传感器的输入输出或多或少的存在非线性问题。为评价传感器实际输出的线性程度，需要人为引入一条拟合基准直线。传感器实际输出与拟合基准直线的最大偏差称为非线性误差或线性度[2]。因此，拟合的基准直线对传感器的线性度影响非常大。也就是说，同样的传感器输出数据，选择不同的拟合基准直线，得到的非线性误差就不同。针对磁弹性传感器的输出特性，需要选取恰当的拟合基准直线来计算线性度。本文将探讨并确定最优的拟合直线。

1 磁致伸缩

1842年，焦耳(J.P.Joule)在试验中发现铁丝在磁场中长度会发生变化，被称为焦耳效应[3]。其物理原理是：铁磁性物质在磁场的作用下，内部磁畴结构的变化引起内部磁通的变化，并产生相应的线性应变，这说明磁致伸缩材料具有将磁能转换为机械能的特性。而维拉里效应是磁致伸缩的逆效应，也被称为铁磁体的压磁性现象。维拉里效应证明应力和磁场一样可使强磁性物质的磁畴发生变化，即可以将机械能转变为电磁能。

磁致伸缩可分为体磁致伸缩和线磁致伸缩。铁磁体的线磁致伸缩如图1所示。

图1 铁磁体的线磁致伸缩示意图Fig.1 Schematic diagram of linear magnetostriction of ferromagnet

2 磁弹性传感器

2.1 磁弹性传感器简介

磁弹性传感器受到机械力F产生弹性应力σ或残余应力作用时，机械力的变化转换成传感器导磁体的导磁率μ变化，也就是引起磁路磁阻Rm的变化，经测量电路处理后输出电压V信号[5]。其一系列变换可以表示成F→σ→μ→Rm→V。磁弹性传感器将力这样的非电量变换成电量，所以也有学者将其叫做压磁式传感器，在日本称其为磁应变计[6]。

磁弹性传感器结构牢靠、便于制造，且输出功率大、信号强，能在恶劣的工况条件下使用。磁弹性传感器不仅可以测量压力，而且可附着在杆件上进行无损应力测量，较之X射线方法、开槽法、钻孔法及电阻丝片应变法有很大的优点。测量误差已经可以降低到1%以下。与电阻应变式压力传感器相比，磁弹性传感器不需要进行粘贴应变片这种相对复杂的操作，且过载能力强，为额定负载的3～10倍。

磁弹性传感器根据电磁原理可分为:魏德曼式、阻流圈式、变压器式、巴克豪森式、桥式和电阻式传感器，各向异性压磁式传感器是变压器式的一种。磁弹性传感器广泛应用在称重、冶金、造纸等行业，尤其用来测量轧钢机的轧制力、钢带的张力、纸张的张力，物料的按质量配料装置、起重运输的过载保护系统、吊车提物的自动配重等。

2.2 各向异性磁弹性传感器的物理结构

磁弹性传感器是一种磁性载荷传感元件，根据磁性材料在机械力作用下磁导率变化的原理，对于正磁致伸缩的材料，其受压时沿应力方向的磁导率下降，而与应力垂直方向的磁导率增大，受拉时效果相反。传感器由许多片大小相同的硅钢片层叠构成，中间的四个孔交叉穿绕导线，形成空间上正交的两组线圈。这种传感器像是一种“设计错了”的变压器。其中一次线圈和二次线圈在无外力加载的状况下，其电磁耦合为零。各向异性磁弹性传感器示意图如图2所示。

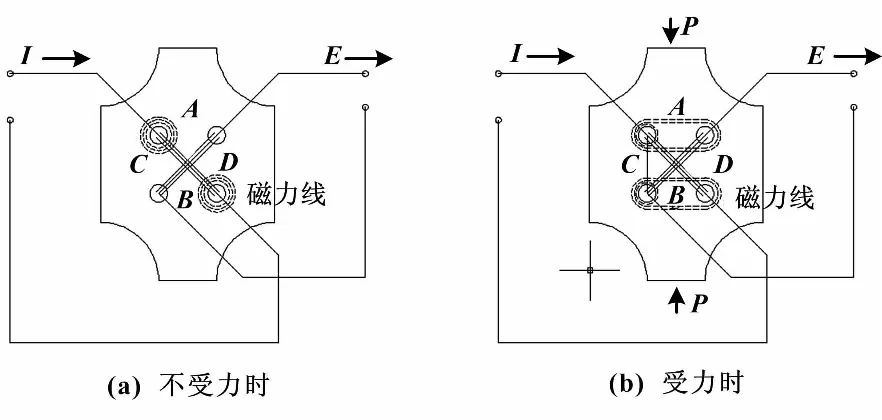
图2 各向异性磁弹性传感器示意图Fig.2 Schematic diagram of anisotropic magnetoelastic sensor

硅钢片相互垂直地开有两对孔(孔1、2和孔3、4)，孔1、2之间饶有励磁线圈W12，孔3、4之间绕有测量线圈W34，当励磁绕组线圈输入励磁电流后，铁芯中就产生磁场。为了方便分析，把孔间分为A、B、C、D四个区域。传感器在不受力时，由于铁芯中磁的各向同性，A、B、C、D四个区域的磁导率是相同的;这时,磁力线呈轴对称分布，合成磁场强度H平行于测量线圈W34的平面，磁力线不与测量线圈W34交链，因而不产生感应电势。

在压力P的作用下，A、B区受到很大的压应力σ，而C、D区基本上处在自由状态。根据维拉里效应，A、B区的磁导率μ下降，磁阻增大，而C、D区的磁导率μ不受影响。这就促使部分的磁力线不再通过A、B区域闭合反而通过C、D区域闭合。于是磁力线被扭曲变形，合成的磁场强度H不再与平面W34平行，而与测量线圈交链。测量线圈W34中感应出的电动势E随着压力值P变化，压力越大转移磁通越多，E值也就越大。感应电动势E经过信号电路处理后，就能建立压力P与输出电压V的线性关系。正是由于磁的各向异性特征,这种传感器被称为磁各向异性传感器。磁弹性传感器用于测量或控制压力，本体直接承受荷载,所以也称压头传感器,或简称压头。

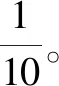
2.3 各向异性磁弹性传感器的电气特性

磁弹性传感器的工作过程是一个复杂的变换过程，期间涉及力学、磁学、电学等物理现象。磁弹性传感器的变换过程至今仍未得到准确的数学模型，尤其是应力与磁导率之间的数理关系。虽然不能用纯粹的理论推导对压磁式传感器进行计算，但是可以通过试验-分析的方法来确定其主要参数。

传感器受力时的内部磁场如图3所示。

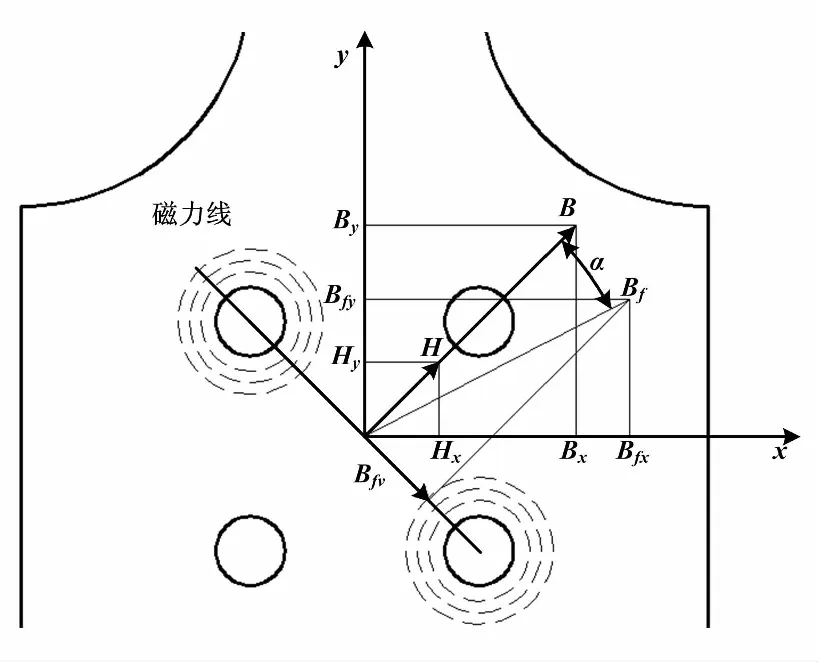
图3 传感器受力时的内部磁场Fig.3 Internal magnetic field when the sensor is under force

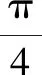
(1)

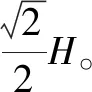
(2)

磁感应强度为：

(3)

此时，在测量线圈的平面内，磁通与测量线圈没有磁耦合，因此测量线圈中没有感应电势。当传感器沿y轴受力时，其内部产生应力σ，该方向的磁导率降低Δμf。其数值为：

Δμf=μfλ0μHσ

(4)

式中:μf为铁芯受力时沿受力轴的磁导率；λ0为初始磁致伸缩率。

沿x轴的磁导率变化很小，即Bfx≈Bx,则沿y轴的磁感应强度变化为:

Bfy=(μH-Δμf)Hy

(5)

磁感应强度为:

(6)

磁感应强度偏转一个角度α，引起测量线圈的磁通量变化，致使测量线圈有感应电势输出。对输出电压已有学者作过详尽的推导[7]，此处直接表示为：

(7)

式中:i为励磁电流；f为励磁电流的频率；N2为测量线圈的匝数；A2为测量线圈围绕的铁芯截面积；l为磁通的平均长度。

可以看出，在确定的已知条件下，测量线圈的输出电压U2是应力σ的线性函数，即:

U2=Kσ

(8)

式中：K为常数，可以通过试验确定。

励磁电流的频率直接影响传感器的测量响应时间。已知机械应力在固体中的传播速度为声速c。当有一个阶跃式的作用力加载在高度为L的传感器时，力传播的时间可以表示为:

(9)

声音在硅钢片中的传播速度约为5 000 m/s。假设传感器的高度为10 cm，则力在传感器中的传播时间为0.2 ms。励磁电流的频率可以设定在5 kHz以下。

3 磁弹性传感器的线性度

3.1 线性度的计算方法

传感器的线性度、重复性、回差(或称迟滞、迟后)及灵敏度是衡量传感器静态特性的最重要的几个指标[8]。国家标准GB/T 18459-2001《传感器主要静态性能指标计算方法》中对线性度定义为:正、反行程实际平均特性曲线相对于参比直线(拟合直线)的最大偏差,用满量程输出的百分比来表示。国家标准同时指出,根据不同的拟合直线,有不同的线性度[7-11]。

线性度参比直线的拟合方法主要有端点连线拟合、最小二乘法拟合、独立直线拟合和平均选点直线拟合[12]。端点连线拟合将传感器测量输出数据的起点和满量程输出点作为直线的两个端点，起点和满量程点可以取多次测量的平均值。该方法较为简单，但误差分布不均匀,在生产工厂中应用较多[13-15]。最小二乘法拟合是使传感器输出数据与拟合直线各个点之间的残差为最小值。拟合直线方程为：

y=kx+b

(10)

式中:x为被测量的值；y为拟合输出值；k和b为待定拟合参数[14]。

最小二乘拟合的特点是计算繁杂，但拟合精度高、所求得的非线性误差数值小、很多学者认为由最小二乘法求得的理论值跟实际值的误差最小,是最优的。独立直线是传感器正反行程测量时输出的两组数据平行线的中线位。平均选点直线将测量数据分成前后两组，每组中求平均值确定一个点，以构成一条直线。

3.2 各种拟合方法的比较

对于各向异性磁弹性传感器，采用不同线性度拟合直线所得出的非线性误差也就不同。试验的最大加载力为22 kN，测试数据和非线性误差如表1所示。

表1 测试数据和非线性误差Tab.1 Test data and nonlinear error

表1中：L、S1、S2、E1、E2、E3、E4和E5分别代表加载力(KN)、传感器进程输出电压(mV)、传感器回程输出电压(mV)、端点连线拟合误差(%)、最小二乘法拟合误差(%)、独立直线拟合误差(%)、平均选点误差(%)和端点平移拟合误差(%)。可以看出，端点连线拟合、最小二乘法拟合、独立直线拟合和平均选点直线拟合的非线性误差分别为2.07%、-1.79%、2.3%和-2.07%。传感器输出和拟合直线如图4所示。

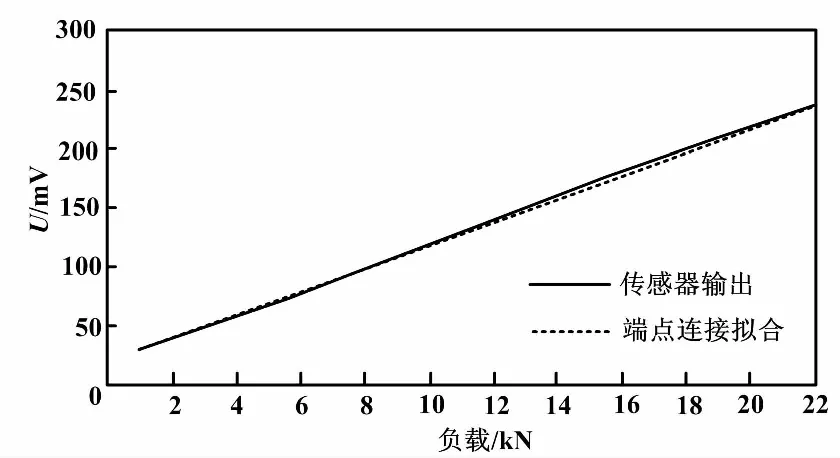
图4 传感器输出和拟合直线Fig.4 Sensor output and fit line

最小二乘法拟合直线的非线性误差优于端点连线法，但是在末端误差数据较大。这是因为采用最小二乘法处理数据，求的是各个点的偏差的平方和最小，是总体最小，而非线性误差的定义是最大偏差与满量程的比值，是一个局部点，所以最小二乘法拟合直线并不一定是最好的非线性误差参比直线。独立直线拟合和平均选点直线拟合法得出的非线性误差也不是最优的。

由于受到磁饱和的影响，磁弹性传感器的灵敏度随负载增加而降低，即测试输出曲线为一条略微突起的曲线。这是这类传感器的普遍现象，会导致端点连线法得出的非线性误差大部分都为正值。可以想象，将端点连线平移升高，可以使非线性误差正负均分，从而降低误差数值。如果将端点连线拟合定义为:

yt=ktx+y0

(11)

式中:yt为拟合值；kt为斜率；x为测量的力值；y0为传感器的零点输出。

偏移量定义为:

(11)

式中:ym和ytm分别为最大非线性误差处传感器的测量值和拟合值。端点平移拟合直线yto为:

yto=kt+ys

(12)

采用端点平移法计算得出的数据列在表1中，非线性误差为-1.62%，是较适合各向异性磁弹性传感器的直线拟合方法。这种将拟合直线调整到使偏差最小的方法也被称为独立线性度,或最佳拟合直线。

4 结论

近年来,磁弹性传感器在冶金等行业得到越来越多的应用，并且相当成功。同时也要注意到，磁弹性传感器的理论研究还有很多的工作要做，尤其是压力与磁导率之间的数理关系尚无确切的定义。非线性误差是传感器的关键指标，直接影响产品的定级。分析磁弹性传感器的线性度时，采用端点平移拟合法可提高其线性度。